26
Пояснительная записка
Статус документа
С целью сохранения единого образовательного пространства, повышения качества образования Рабочая программа по курсу «Математика» для юридического профиля ФГКОУ НСВУ МВД России разработана в соответствии с Примерной программой по математике, рекомендованной в Письме Департамента государственной политики в образовании Минобрнауки России от 7 июля 2005 г. № 03-1263, с учетом федерального компонента государственного стандарта среднего (полного) общего образования на базовом уровне.
Рабочая программа по курсу «Математика» составлена на основе следующих нормативных документов:
Приказ Министерства образования Российской Федерации от 05 марта 2004 г. № 1089 "Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования";
Приказ Министерства образования Российской Федерации от 05 марта 2004 г. № 1089 об утверждении Стандарта среднего (полного) общего образования по математике;
Приказ Министерства образования Российской Федерации от 09.03.2004г. №1312 «Об утверждении Федерального базисного учебного плана и примерные учебных планов для общеобразовательных учреждений РФ, реализующих программу общего образования».
Приказ Министерства образования и науки РФ от 31 .03.2014 года №253 «Об утверждении федерального перечня учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2014/2015 учебный год».
Учебный план ФГКОУ НСВУ МВД России на 2014-2015 учебный год.
Структура документа
Рабочая учебная программа по математике включает: пояснительную записку; общую характеристику учебного предмета, место учебного предмета в учебном плане; содержание учебного предмета; учебно-тематическое планирование; результаты освоения программы; учебно-методическое и материально-техническое обеспечение образовательной деятельности; приложение к программе: календарно-тематическое планирование.
Программа соответствует учебнику А. Г. Мордкович. Математика. 10 класс: учебник для общеобразовательных учреждений /А.Г. Мордкович, И.М. Смирнова. – М.: Мнемозина, 2004-2010 г.
Содержание программы направлено на освоение обучающимися знаний, умений и навыков на базовом уровне, что соответствует Образовательной программе, реализуемой ФГКОУ НСВУ МВД России.
Программа выполняет две основные функции.
Информационно-методическая функция позволяет всем участникам образовательной деятельности получить представление о целях, содержании, общей стратегии обучения, воспитания и развития суворовцев средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации обучающихся.
Цели изучения
курса «Математика» на 2 курсе НСВУ МВД России:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения естественнонаучных дисциплин на базовом уровне, для получения образования в областях, требующих математической подготовки на базовом уровне;
воспитание средствами математики культуры личности; отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Задачи обучения:
приобретение математических знаний и умений;
овладение обобщенными способами мыслительной, творческой деятельностей;
Общая характеристика учебного предмета
Данный курс математики предназначен для обучающихся, ближайшее будущее которых не будет связано с изучением математики в высшей школе. Он представляет собой модификацию содержания базового курса на «общекультурном» уровне.
«Общекультурная» составляющая курса усилена за счет включения дополнительных историко-культурных и практических вопросов. В математической составляющей курса выделены важнейшие понятия, которые позволяют построить логическое завершение школьного курса математики. При этом значительная часть материала, который в обязательном минимуме содержания основных образовательных программ стандарта выделен курсивом, снят из основного содержания рабочей программы.
Требования, выделенные курсивом в стандарте, не предъявляются к выпускникам, обучающимся по программам для общекультурного уровня.
Рабочая программа определяет инвариантную (обязательную) часть содержания образования учебного курса «Математика», задаваемую УМК авторов А.Г. Мордковича и И.М. Смирновой. Этим самым программа содействует сохранению единого образовательного пространства.
В данном курсе представлены содержательные линии "Алгебра", "Функции", "Начала математического анализа", "Уравнения и неравенства", "Геометрия", "Элементы комбинаторики, теории вероятностей, статистики и логики".
В рамках указанных содержательных линий определены цели изучения курса «Математика» на 2 курсе НСВУ МВД России.
Место предмета в учебном плане
Рабочая программа по математике составлена на основе учебного плана ФГКОУ НСВУ МВД России, в котором предмет «математика» представлен в инвариантной части. Согласно учебному плану для изучения курса «Математика» отводится 140 ч из расчета по 4 ч в неделю на 2 курсе.
При этом предполагается построение курса в форме последовательности тематических блоков с чередованием материала по алгебре, анализу, дискретной математике, геометрии.
Общеучебные умения, навыки и способы деятельности
В ходе освоения содержания курса «Математика» обучающиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
На 2 курсе существенно повышаются требования к рефлексивной деятельности обучающихся: к объективному оцениванию своих учебных достижений, поведения, черт своей личности, понимать ценность образования как средства развития культуры личности суворовца.
В процессе обучения должно быть сформировано умение излагать свои мировоззренческие взгляды и на этой основе – воспитание гражданственности и патриотизма.
Содержание учебного предмета 140ч.
АЛГЕБРА
Происхождение натуральных чисел и арифметических действий над ними. Расширение понятия числа как необходимость создания математического аппарата для решения насущных и потенциальных задач практики человека.
История изобретения отрицательных и иррациональных чисел и десятичных дробей. Развитие и систематизация сведений о действительных числах.
Корни и степени
Корень степени n1 и его свойства. Степень с рациональным показателем и ее свойства.
Основы тригонометрии
Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Преобразования простейших тригонометрических выражений.
Решение простейших тригонометрических уравнений.
Арксинус, арккосинус, арктангенс числа.
ФУНКЦИИ
Сложные процессы в природе и обществе и необходимость создания специального математического аппарата – дискретных и непрерывных моделей – для их количественного описания.
Функции
Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация.
Понятие обратной функции.
Степенная функция
Определение степенной функции с натуральным показателем, её свойства и график.
Тригонометрические функции
Определение тригонометрических функций: у = sinx, у = cosx, y=tqx, y=ctqx, их свойства и графики; периодичность, основной период.
Периодические процессы и их описание с помощью тригонометрии.
Показательная функция
Определение показательной функции (экспонента), её свойства и график.
Примеры функциональных зависимостей в реальных процессах и явлениях: равномерные и равноускоренные процессы и их описание с помощью линейных и квадратичных функций; процессы экспоненциального роста. Геометрическая прогрессия как пример дискретного процесса быстрого роста. Легенда о создании шахмат, сложные проценты, примеры быстрого роста в живой и неживой природе.
Преобразования графиков: параллельный перенос, симметрия относительно осей координат.
НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма.
Понятие о производной функции
Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков на примере многочленов.
Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком. Примеры применения интеграла в физике и геометрии. Вторая производная и ее физический смысл.
УРАВНЕНИЯ И НЕРАВЕНСТВА
Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных уравнений.
Основные приемы решения систем уравнений:
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной.
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов.
ГЕОМЕТРИЯ
Прямые и плоскости в пространстве. Основные понятия стереометрии (точка, прямая, плоскость, пространство).
Пересекающиеся, параллельные и скрещивающиеся прямые
Пересекающиеся, параллельные и скрещивающиеся прямые. Угол между прямыми в пространстве.
Перпендикулярность прямых. Параллельность и перпендикулярность прямой и плоскости, признаки и свойства. Теорема о трех перпендикулярах. Перпендикуляр и наклонная. Угол между прямой и плоскостью.
Параллельность плоскостей, перпендикулярность плоскостей
Параллельность плоскостей, перпендикулярность плоскостей, признаки и свойства. Двугранный угол, линейный угол двугранного угла.
Расстояния от точки до плоскости. Расстояние от прямой до плоскости. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми.
Параллельное проектирование
Параллельное проектирование. Изображение пространственных фигур.
Многогранники.
Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера.
Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб.
Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида.
Симметрии в кубе, в параллелепипеде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Примеры симметрий в окружающем мире.
Сечения куба, призмы, пирамиды.
Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Аксиоматика
Аксиомы, определяемые и неопределяемые понятия. Теоремы. Аксиоматика в математике и в повседневной жизни. Евклидова геометрия и геометрия Лобачевского.
Координаты и векторы
Декартовы координаты в пространстве. Формула расстояния между двумя точками.
Учебно-тематическое планирование
Распределение учебного времени по полугодиям,
темам и видам учебных занятий
|
№ п/п |
Номера и наименование разделов и тем. | Всего часов | Из них по видам учебных занятий | Зачет, Экзамен | Тесты |
| Лекции | Уроки | Лабораторные самостоятельные работы | Семинары | к.р. |
|
|
|
| II курс I полугодие. |
|
|
|
|
|
|
|
|
| 1. | Первый блок. Повторение. Числовые функции | 6 |
| 6 | (2) |
|
|
|
|
| 2. | Второй блок. Начала стериометрии. | 12 | 1 | 10 | (2) |
| 1 |
|
|
| 3. | Третий блок. Тригонометрические функции углового аргумента. | 13 | 1 | 11 | (2) |
| 1 |
|
|
| 4. | Четвертый блок. Сечение многогранников. | 10 | 1 | 8 | (2) |
| 1 |
|
|
| 5. | Пятый блок. Тригонометрические функции и их свойства. | 10 | 1 | 8 | (2) |
| 1 |
|
|
| 6. | Шестой блок. Тригонометрические уравнения. | 10 |
| 9 | (3) |
| 1 |
|
|
|
| Всего за I полугодие. | 61 | 4 | 52 | (13) |
| 5 |
|
|
|
| II курс II полугодие |
|
|
|
|
|
|
|
|
| 1. | Седьмой блок. Ортогональное проектирование. | 9 | 1 | 7 | (2) |
| 1 |
|
|
| 2. | Восьмой блок. Тригонометрические преобразования. | 13 |
| 12 | (3) |
| 1 |
|
|
| 3. | Девятый блок. Многогранники. | 14 | 1 | 12 | (3) |
| 1 |
|
|
| 4 | Десятый блок. Производная. | 21 | 2 | 18 | (4) |
| 1 |
|
|
| 5. | Одиннадцатый блок. Применение производной. | 7 |
| 6 |
|
| 1 |
|
|
| 6. | Двенадцатый блок. Обобщающее повторение. | 15 |
| 13 | (2) |
|
| 2 |
|
|
| Всего за II полугодие: | 79 | 4 | 68 | (9) |
| 5 | 2 |
|
|
| Всего за II курс: | 140 | 8 | 120 | (21) |
| 10 | 2 |
|
Тематическое планирование составлено к УМК А. Г. Мордковича и И.М Смирновой. «Математика», 10, М. «Мнемозина», 2012 год на основе федерального компонента государственного стандарта общего образования (Приказ Минобрнауки. №413 от 17 мая 2012 года) с учетом авторского тематического планирования учебного материала, приведенного в учебнике.
Результаты освоения программы
учебного предмета «математика»
Требования к уровню подготовки обучающихся II курса
В результате изучения математики на базовом уровне в старшей школе обучающийся должен
Знать/понимать:
значение математической науки для решения задач, возникающих в теории и в практике; широту и, в то же время, ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности.
Алгебра
Уметь:
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, при необходимости используя справочные материалы и простейшие вычислительные устройства.
Функции и графики
Уметь:
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решать уравнения, простейшие системы уравнений, используя их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.
Начала математического анализа
Уметь:
вычислять производные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов с использованием аппарата математического анализа;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения прикладных, в том числе социально-экономических и физических, задач на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Уравнения и неравенства
Уметь:
решать тригонометрические уравнения и неравенства;
составлять уравнения по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для построения и исследования простейших математических моделей.
Геометрия
Уметь:
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур.
Система оценивания ответов обучающихся
Оценка ответа обучающегося при устном и письменном опросе проводится по четырех бальной системе, т.е. за ответ выставляется одна из отметок: 2(неудовлетворительно), 3 (удовлетворительно), 4 (хорошо), 5(отлично).
Оценка устных ответов обучающихся
Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а его изложение и письменная запись математически грамотны, логически последовательны и аккуратны.
| Выставляется отмет- ка |
Если: (критерии) |
| «5» | в полном объеме раскрыто содержание материала, предусмотренное программой и учебником; материал изложен логически последовательно, грамотным языком с точным использованием математической терминологии и символики; правильно выполнены в соответствии с ответом рисунки, чертежи, графики; теоретические положения проиллюстрированы конкретными примерами и умением их применения в новой ситуации; возможны две неточности при освещении второстепенных вопросов, которые обучающийся легко исправил по замечанию преподавателя. |
| «4» | при освещении основного содержания ответа допущены небольшие пробелы, не исказившие математическое содержание ответа; в изложении материала возможны два- три недочета, исправленные по замечанию преподавателя; при освещении второстепенных вопросов допущена ошибка или более двух недочетов, исправленные по замечанию преподавателя. |
| «3» | неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрировано умение, соответствующие «Требованиям к математической подготовке обучающихся»; имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов преподавателя; отвечающий не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня по данной теме; при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков. |
| «2» | не раскрыто основное содержание учебного материала; незнание или непонимание отвечающим большей или наиболее важной части учебного материала; допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках или графиках, выкладках, которые не исправлены после наводящих вопросов преподавателя. |
Критерии ошибок
К грубым ошибкам относятся ошибки, которые показывают:
незнание обучающимися формул, правил, основных свойств и теорем и неумение их применять;
незнание приемов решения задач, рассматриваемых в учебнике;
вычислительные ошибки, если они допущены в подлежащих контролю вычислениях.
К негрубым ошибкам относятся:
потеря корня или сохранение в ответе постороннего корня уравнения;
отбрасывание постороннего корня без объяснения;
вычислительные ошибки, не повлиявшие на алгоритм выполнения задания.
К недочетам относятся:
нерациональное решение;
описки;
недостаточность или отсутствие пояснений, обоснований в решениях.
Оценка письменных работ обучающихся
Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
| Выставляется отметка |
Если: (критерии) |
| «5» | работа выполнена полностью; решение изложено логически последовательно, грамотным языком с точным использованием математической терминологии и символики; правильно выполнены в соответствии с ответом рисунки, чертежи, графики; возможны одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала. |
| «4» | работа выполнена полностью, но обоснование шагов решения недостаточны; допущена одна ошибка или три недочета в выкладках, рисунках, чертежах или графиках при условии, что данный материал не являлся специальным объектом проверки. |
| «3» | допущены более одной ошибки или более трех недочетов, но обучающийся владеет обязательными умениями по проверяемой теме. |
| «2» | допущены существенные ошибки, показавшие, что обучающийся не владеет обязательными умениями по данной теме в полной мере; значительная часть работы выполнена не самостоятельно. |
Контрольно-измерительные материалы
Контрольная работа № 1 Вариант 1
1. Прямые a и b пересекаются. Докажите, что прямая c, пересекающая их в двух различных точках, лежит с ними в одной плоскости.
2. Можно ли провести через точку пересечения диагоналей прямоугольника прямую, которая не пересекает его сторон?
3. Сторона AC треугольника ABC лежит в плоскости α. Вершина B не принадлежит этой плоскости. Докажите, что прямая, проходящая через середины сторон AB и BC, параллельна плоскости α.
4. Через точку K, не лежащую между параллельными плоскостями a и β, проведены прямые a и b. Прямая a пересекает плоскости a и β в точках A1 и A2 соответственно, прямая b - в точках B1 и B2. Найдите отрезок B1B2, если A2B2:A1B1=9:4, KB1=8см.
5*. Докажите, что если плоскость пересекает одну из параллельных плоскостей, то она пересекает и другую плоскость.
Вариант 2
1. Даны четыре точки, три из которых принадлежат одной прямой. Докажите, что все данные точки принадлежат одной плоскости.
2. Можно ли через вершину треугольника провести прямую, которая не лежит в его плоскости?
3. Через основание AD трапеции ABCD проведена плоскость . Основание BC не лежит в плоскости . Докажите, что прямая, проходящая через середины сторон AB и CD, параллельна плоскости .
4. Через точку M, лежащую между параллельными плоскостями и , проведены прямые a и b. Прямая a пересекает плоскости и в точках A1 и A2 соответственно, прямая b - в точках B1 и B2. Найдите отрезок MB2, если A1B1:A2B2=3:4, B1B2=14 см.
5*. Докажите, что если прямая пересекает одну из параллельных плоскостей, то она пересекает и другую плоскость.
Контрольная работа № 2
Вариант 1
Вычислите: а)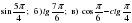 ;
;
г) 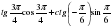 ; д)
; д) 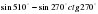 .
.
Упростите выражение 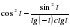 .
.
Решите уравнение: а) 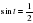 ; б)
; б) 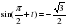 .
.
______________________________________________________________
Известно, что 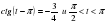 .
.
Найдите 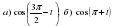 .
.
____________________________________________________________
5. Расположите в порядке возрастания следующие числа:
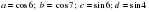 .
.
Вариант 2
1. Вычислите: а)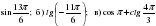 ;
;
г) 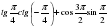 ; д)
; д) 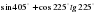 .
.
2. Упростите выражение 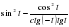 .
.
3. Решите уравнение: а) 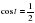 ; б)
; б) 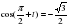 .
.
____________________________________________________________
4. Известно, что 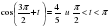 .
.
Найдите 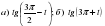 .
.
_____________________________________________________________
5. Расположите в порядке убывания следующие числа:
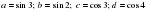 .
.
Контрольная работа № 3
Вариант 1
Постройте точку пересечения прямой MN
а) с плоскостью (ADC) б) с плоскостью (AA1B1)


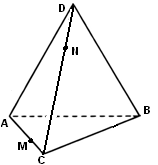
Постройте сечение многогранника плоскостью, проходящей через точки M, N и K






















Вариант 2
Постройте точку пересечения прямой MN
а) с плоскостью (ABD) б) с плоскостью (A1B1C1)



Постройте сечение многогранника плоскостью, проходящей через точки M, N и K






















Контрольная работа № 4
Контрольная работа № 5
|
Вариант 1
|
Вариант 2 |
Решите уравнения: 1.  , , | Решите уравнения: 1.  , , |
| 2. ,
| 2. ,
|
| 3. ,
| 3. ,
|
| 4. =0 =0
| 4.  |
 
| 5.   , , |
| 6. sin x⋅cos x+2sin2x =cos2x | 6. sin2x =2 sin x⋅cos x+cos2x
|
| 7. Найдите корни уравнения sin 3x=cos3x, принадлежащие отрезку [0; 4].
| 7. Найдите корни уравнения  , принадлежащие отрезку [-1; 6]. , принадлежащие отрезку [-1; 6]. |
Контрольная работа №6
Вариант 1
В кубе A…D1 найдите угол между прямыми: а) AB и BB1; б) AB1 и CC1; в) AB1 и CD1.
Дана плоскость α. Из точки A проведены к ней две наклонные AB = 20 см и AC = 15 см. Проекция наклонной AB на эту плоскость равна 16 см. Найдите проекцию второй наклонной.
Из точки М проведен перпендикуляр MB к плоскости прямоугольника ABCD. Докажите, что треугольник AMD прямоугольный.
Дан прямоугольный параллелепипед АВСDA1B1C1D1. Найдите двугранный угол B1ADB, если известно, что четырехугольник АВСD - квадрат, АС=  см, АВ1=
см, АВ1= см.
см.
Вариант 2.
В кубе A…D1 найдите угол между прямыми: а) BC и BB1; б) A1C1 и AD; в) A1D и BC1.
Наклонная, проведенная к плоскости, равна 6 см. Найдите ортогональную проекцию этой наклонной на плоскость, если угол между наклонной и плоскостью равен 300.
Прямая АК перпендикулярна к плоскости прямоугольного треугольника ABC (C=90°). Докажите, что треугольник KBC прямоугольный.
Дан прямоугольный параллелепипед АВСDA1B1C1D1. Найдите двугранный угол А1DСА, если АС=13 см, DC=5 cм, АА1= см.
см.
Контрольная работа №7
Вариант 1.
1. Найдите значение выражений:
а) ;
б) .
2. Упростите выражение:
.
3. Решите уравнение:
а)
б)
4. Докажите тождество
5. Вычислите:
6. Решите уравнение:

Вариант 2.
1. Найдите значение выражений:
а) co7;
б) .
2. Упростите выражение: .
3. Решите уравнение:
а)
б)
4. Докажите тождество
5. Вычислите:

6. Решите уравнение:
Контрольная работа №8
Вариант 1.
Вычислите площадь поверхности икосаэдра, ребро которого равно a.
Нарисуйте выпуклый многогранник с 5 вершинами.
Нарисуйте: а) развертку тетраэдра; б) многогранник, двойственный гексаэдру.
Высота правильной четырехугольной пирамиды равна 8 см, сторона ее основания - 12 см. Найдите боковое ребро пирамиды.
Через два противолежащих ребра куба проведено сечение, площадь которого равна  см2. Найдите ребро куба и его диагональ.
см2. Найдите ребро куба и его диагональ.
6*. Докажите, что сумма квадратов диагоналей прямоугольного параллелепипеда равна сумме квадратов всех его ребер.
Вариант 2.
Вычислите площадь поверхности октаэдра, ребро которого равно a.
Нарисуйте выпуклый многогранник с 6 вершинами
Нарисуйте: а) развертку куба; б) многогранник, двойственный тетраэдру.
Боковое ребро правильной четырехугольной пирамиды равно 15 см, сторона ее основания - 18 см. Найдите высоту пирамиды.
Ребро куба равно 6 см. Найдите диагональ куба и площадь сечения, проходящего через диагонали двух его противолежащих граней.
6*. Докажите, что сумма квадратов площадей диагональных сечений прямоугольного параллелепипеда равна сумме квадратов площадей его боковых граней.
Контрольная работа №9
Итоговая контрольная работа
Вариант №1.
А1. Упростите выражение: sin2 х + 4 + cos2 х.
1)3 2) 4 3) 5 4) 6
А2. Решите уравнение: 2соsx -1 = 0.
1) ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 
АЗ. Найдите множество значений функции у = 4 + 2sin4x.
1) [-4;12] 2) [2;6] 3) [-2; 2] 4) [-4; 4]
А4. Найдите значение производной функции y = 2 соsx - 12 в точке х0= 0.
1) 12 2) -10 3) 0 4) 2
А5. Найдите угловой коэффициент касательной, проведенной к графику функции
у =
 точке с абсциссой
точке с абсциссой  .
.
1). -1 2)  3) 0 4) 1
3) 0 4) 1
B1. Точка движется по координатной прямой согласно закону S(t) = t 3 + t2 + 2. В какой момент времени t скорость точки будет равна 
B2. Найдите точку максимума функции  .
.
B3. Найдите значение cos t, если sint = 
С1. а).Решите уравнение: соs2 2x + 3соs 2x + 2 = 0.
б).Найдите все корни этого уравнения, принадлежащие промежутку [0; 2 ].
].
Вариант №2.
А1. Упростите выражение: sin2 х+ 4 + sin2 х∙ctg2x.
1)4 2) 4cos2x 3) 5 4) 4sin2 х
А2. Решите уравнение:  .
.
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 
АЗ. Найдите множество значений функции у = 1,5 - 2sin3x.
1) [-0,5; 3,5] 2) [-3,5; 3,5] 3) [-2; 2] 4) [-4; 4]
А4. Найдите значение производной функции y = -4 sinx-5 в точке х0= π.
1) -5 2) -4 3)-1 4) 4
А5. Найдите угловой коэффициент касательной, проведенной к графику функции
h(x)=х6-4x, в точке x0=1
1) 26 2) 10 3) 2 4) 1
B1. Точка движется по координатной прямой согласно закону s(t) = t 3 - 5t2 +6t + 7.В какой момент времени t скорость точки будет равна 
B2. Найдите точку минимума функции  .
.
В3. Найдите значение cos t, если sin t = - 0,6;

С1. Решите уравнение: tq2x + 5tqx +6 = 0 и найдите корни, принадлежащие отрезку  .
.
Учебно-методическое и материально-техническое обеспечение предмета
Учебно-методическое обеспечение.
10 класс:
Александрова, Л. А. Алгебра и начала анализа. 10 класс: самостоятельные работы. / JI. А. Александрова. - М.: Мнемозина, 2013.
Атанасян, Л.С. Изучение геометрии в 10-11 классах / J1. С. Атанасян, В. Ф. Бутузов. - М., 1999.
Ершова, А. П. Самостоятельные и контрольные работы. Алгебра и начала анализа. 10 класс-11 класс / А. П. Ершова, В. В. Голобородько. - М., 2008.
Мордкович, А. Г. Математика. 10 класс: учебник для общеобразовательных учреждений / А. Г. Мордкович, И. М. Смирнова. - М.: Мнемозина, 2011.
Дополнительные пособия для обучающихся:
5.Лысенко, Ф. Ф. Математика. ЕГЭ -2013: учебно-тренировочные тесты / Ф. Ф. Лысенко. - Ростов-на-Дону: Легион.
6. Лысенко, Ф. Ф. Математика. ЕГЭ -2013: тематические тесты / Ф. Ф. Лысенко. - Ростов-на-Дону: Легион.
7. Энциклопедия для детей. Т. 11. Математика, М., 1998.
Дополнительные пособия для преподавателя:
8. Математика в школе. Ежемесячный научно-методический журнал.
9. Математика. Еженедельное приложение к газете «Первое сентября».
Информационные источники
Для информационно-компьютерной поддержки образовательной деятельности предполагается использование следующих программно-педагогических средств, реализуемых с помощью компьютера:
Министерство образования РФ: http://www.informika.ru/; http://www.edu.ru/
Тестирование online: 5-11 классы: http://www.kokch.kts.ru/cdo/
Педагогическая мастерская, уроки в Интернете и многое другое: http://teacher
Новые технологии в образовании: http://edu.secna.ru/main/
Путеводитель «В мире науки» для школьников: http://www.uic.ssu.samara.ru -пая
Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru
сайты «Энциклопедий», например: http://www.rubricon,ru/: http://www.encycloped
Материально-техническое обеспечение
Технические средства обучения: Мультимедийный проектор, экспозиционный экран, персональный компьютер.
Экранно-звуковые пособия: мультимедийные цифровые образовательные ресурсы, соответствующие тематике, виртуальные лаборатории (геометрическое конструирование и моделирование.)
Оборудование класса: Классная доска с набором приспособлений для крепления таблиц, ученические столы 1-2 местные с комплектом стульев, шкафы для хранения учебников, дидактических материалов, пособий.
Согласовано
Заместитель начальника училища
по учебной работе
ххххххххххххххххххххххххххххх
«___ » 2014 года


 Получите свидетельство
Получите свидетельство Вход
Вход


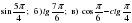 ;
; 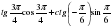 ; д)
; д) 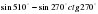 .
.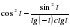 .
.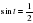 ; б)
; б) 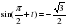 .
.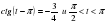 .
. 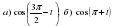 .
.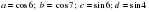 .
.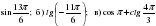 ;
; 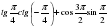 ; д)
; д) 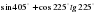 .
.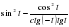 .
.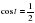 ; б)
; б) 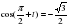 .
.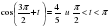 .
. 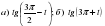 .
.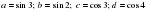 .
.











 Рабочая программа по математике (10 класс, юридический профиль) (0.44 MB)
Рабочая программа по математике (10 класс, юридический профиль) (0.44 MB)
 0
0 406
406 9
9 Нравится
0
Нравится
0



