«Оригами-геометрия бумажного листа»

Введение

В детстве, когда я еще ходила в детский сад, я видела как мама и старшая сестра складывали бумагу в определенной последовательности , в результате чего получалась интересная поделка или фигурка из бумаги. Я помогала отсчитывать нужное количество бумажных прямоугольников для определенных поделок. Так, я еще до школы познакомилась с математикой. К первому классу, я уже знала сколько сторон и углов у квадрата, прямоугольника, треугольника и других фигур.

Сначала для меня это была просто игра, но со временем я осознала, складывая бумагу в определенной последовательности каждый может познакомиться с основными геометрическими понятиями. Такими как: угол( прямой, острый, тупой); прямая линия, сторона фигуры, вершины и многими другими.

В седьмом классе мы с одноклассниками будем изучать новый предмет “Геометрия”.

Многие опасаются изучать новый предмет, думая что это будет сложно и непонятно.

Я считаю свой проект актуальным, так как он не только поможет при изучении нового предмета, но и заинтересовывает, развивает творческие способности и укрепляет уверенность в своих силах.

Практическая значимость: данного проекта заключается в том, что пользуясь инструкцией пошагового изготовления одноклассники смогут изготовить оригами, научатся делить прямые углы .

Цель: определить значение математики в искусстве оригами

Задачи:

*узнать историю возникновения первых оригами

*изучить литературу видов оригами

*определить и подобрать материал(бумагу) для изготовления различных видов оригами

*выяснить ,как математика помогает при выполнении работ из бумаги.

Гипотеза

Может ли искусство оригами помочь в изучении математики?

Объект исследования: оригаметрия.

Предмет исследования: использование оригами в математике.

Продукт проекта: поделки из разных видов оригами, буклет с пошаговым выполнением простого оригами.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1. История оригами
   О таком виде искусства, как оригами, слышал, наверняка, каждый современный человек. Однако часто даже тот, кто любит проводить свое свободное время, складывая всевозможные фигурки из бумаги, не знает, какой является история оригами, когда и где зародилось это искусство.

Обязательным материалом для данного вида искусства является, естественно, бумага. И хотя первый станок по производству бумаги был изобретен в Китае, история оригами берет свое начало в Японии. Именно японцы в начале 8 века начали складывать различные фигурки. Кстати, в японском языке слово «оригами» означает «сложенная бумага». Стоит отметить, что в те времена бумага являлась очень дорогим материалом, поэтому доступна она была только храмам и монастырям. Монахи делали специальные бумажные коробочки под названием «санбо», в которых приносили жертвы богам. Эти первые поделки оригами изготовлялись без использования каких-либо инструментов, а материалом являлась исключительно бумага.

Через сотню лет после изобретения в Китае бумаги, японцы изобрели свою, превышающую по качеству китайскую. И поняли, что ей можно найти другое применение помимо записи священных текстов – создание нового искусства (см. Приложение 1).
Один из самых ранних известных примеров использования оригами – катасиро, куклы, символические изображения божеств «козлов-отпущения» (см. Прилож. 2).

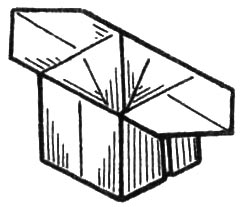
Именно на катасиро японцы мистически переводили все пагубные влияния, такие как порчу и сглазы. Также в Древней Японии имели распространение коробочки из бумаги (санбо), в которых приносили еду в жертву божествам (см. Прилож. 3).

Одной из древнейших также является знакомая всем фигурка журавля (Цуру)(см. Прилож. 4). Существует история о японской девочке из Хиросимы, которую звали Садако. Она верила, что сделав 1000 журавликов, она обретет спасение от лучевой болезни. Однако скоро она поняла, что это ей не поможет, тогда она стала дарить журавликов другим больным.

Каждый журавлик был молитвой, молитвой о спасении жизни человека. В течение своей жизни девочка успела сложить 644 фигурки, после ее смерти дело продолжили ее подруги. Печальная история японской девочки подняла волну детской солидарности во всем мире (см. Прилож. 5). Это движение вызвало интерес к японскому искусству. В 1880 году появился официальный термин – «оригами».

И в середине XX века Акиро Йошидзава создал универсальную «Азбуку оригами», позволившую снять языковой барьер и давшую возможность заниматься оригами большему кругу людей. Сейчас мы представим базовые обозначения Азбуки оригами.

Азбука оригами

1. Сгиб «на себя» (сгиб «долиной») (см. Прилож. 6.1).

2. Сгиб «от себя» (сгиб «горой») (см. Прилож. 6.2).

3. Согнуть и разогнуть (см. Прилож. 6.3).

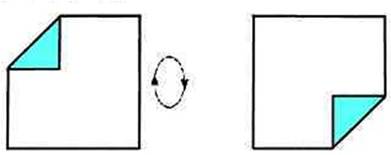
4. Перевернуть на плоскости (см. Прилож. 6.4).

5. Перевернуть на другую сторону (см. Прилож. 6.5).

6. Существующая линия, след сгиба (см. Прилож. 6.6).

7. Линия сгиба «долиной» (см. Прилож. 6.7).

8. Линия сгиба «горой» (см. Прилож. 6.8).

9. Невидимая, скрытая линия.

10. Повторить действие один, два, три раза.

В конце XX века возник новый термин «оригаметрия», обозначающий область геометрии, в которой способом решения задач является складывание. Роль прямых играют края листов и линии сгибов, образующиеся при перегибании, а роль точек - вершины углов листа и точки пересечения сгибов друг с другом или с краями листов.

Теперь перейдем к практической части нашего исследования. В ней мы рассмотрим следующие теоремы и задачи на построение:

• Теорема о сумме углов треугольника

• Теорема о накрест лежащих углах, образованных двумя параллельными прямыми и секущей

• Построение правильного треугольника

• Разделение прямого угла на три равные части

• Катет в прямоугольном треугольнике, лежащий против угла в 30 градусов, равен половине гипотенузы

Немного позже каждый японский аристократ умел делать подобные коробочки для преподнесения подарка дорогому человеку или дани богу. А спустя 600 лет бумага перестала быть столь ценным ресурсом, что позволило данному искусству развиваться большими темпами. История возникновения оригами, наверное, уже давно забыта японцами, однако подаренная ими техника складывания первых самолетиков, фигурок животных и удивительных цветов радует весь мир и сегодня.

    Официальной датой “появления” бумаги в Китае считается 105 г. до н.э.. Тогда же император Хен Сюай  издает специальный указ, запрещающий писать на дереве и предписывающий использовать для письма бумагу. Китайцы ревностно хранили секрет изготовления бумаги в течение 500 лет. Технологию ее производства было запрещено вывозить за границу под страхом смертной казни. Однако, согласно легенде, в начале VII в. н.э. странствующий буддийский монах Дан Хо, о котором современники говорили, что он был “богат знаниями и умел делать бумагу и тушь”, добирается до Японии, и раскрывает секрет бумагоделия. Спустя столетие японцы уже производят собственную бумагу, которая по качеству превосходит китайскую.

  В периоды Адзути-Момояна (1573–1603гг.) и Эдо (1603–1867гг.) бумага перестает быть предметом роскоши и оригами начинает распространяться и среди простого народа. Именно тогда, триста – четыреста лет назад, изобретается ряд фигур, которым суждено было стать классическими. Среди них и японский журавлик «цуру» – традиционный японский символ счастья и долголетия, а теперь и международный символ свободы и мира.

    Искусство оригами в Японии стало традицией, которая передается из поколения в поколение. Историки утверждают, что по манере складывания и набору фигурок можно определить провинцию Японии, в которой выросла и обучалась девушка.

    Первым японским изданием по оригами считается книга «Сенбадзуру ориката», которая вышла в свет в 1797 году. Перевод ее названия “как сложить тысячу журавлей” указывает на старинную легенду, утверждающую, что тысяча сложенных классических бумажных птиц помогает осуществить желания. Книга целиком посвящена складыванию одной единственной модели – журавлика в самых разнообразных ее вариациях. Именно это время характеризуется началом «демократизации» оригами – превращения этого занятия из ритуально-храмового действа в популярный досуг.

    Новый этап в развитии оригами относится ко второй половине XX века и связан с именем знаменитого японского мастера Акиро Йошизава. Акиро Йошизава работал на машиностроительной фабрике, где помимо основной работы, ему поручили учить новичков читать чертежи. При этом он начал активно использовать оригами, объясняя с помощью складывания азы геометрических понятий. Эти занятия имели успех и вызывали неподдельный интерес  и Акире Йошизаве предлагают выступить на съезде профсоюза с рассказом о роли оригами в образовании.

    Акира Йошизава является признанным мировым мастером оригами. Он сделал оригами авторским, придумав сотни оригинальных фигурок. Именно он изобрел единую универсальную систему знаков, с помощью которых можно записать схему складывания любой фигурки.

Новый поворот в истории оригами тесно связано со страшной трагедией, произошедшей 6 августа 1945 года, когда была сброшена атомная бомба на Хиросиму. Последствия чудовищного эксперимента были ужасны. Среди детей, страдающих от последствий облучения и обреченных на гибель, возникла легенда о свободной птице, символе жизни - журавлике. Дети искренне верили, что, смастерив из бумаги 1000 журавликов, они исцелятся и останутся живы. Волна удивительной детской солидарности прокатилась по всем странам мира. Япония стала получать миллионы посылок со всех континентов нашей планеты с бесценным грузом - бумажными журавликами.

Движение «1000 журавликов» вызвало интерес к оригами по всему миру: стали издаваться красочные книги, буклеты, журналы, посвященные этому искусству. Сейчас центры оригами открыты в 26 государствах планеты. Оригами развивается, во многих странах созданы общества оригамистов; каждый год проводятся выставки и конференции.

2.Виды и техники оригами.

Существует пять основных видов оригами: простое оригами, складывание по развертке, мокрое складывание, модульное оригами и киригами.

2.1 Простое оригами

Простое оригами — стиль оригами, придуманный британским оригамистом Джоном Смитом, и который ограничен использованием только складок горой и долиной. Целью оригами является облегчение занятий неопытным оригамистам, а также людям с ограниченными двигательными навыками. Данное выше ограничение означает невозможность многих (но не всех) сложных приёмов, привычных для обычного оригами, что вынуждает к разработке новых методов, дающих сходные эффекты.

Плоские оригами называют также односторонним оригами: предмет определяется только с одной стороны. Обычно такие изделия используются для аппликации. В этом случае используется клей.

2.2 Мокрое оригами

Мокрое складывание - техника складывания, разработанная Акирой Ёсидзавой и использующая смоченную водой бумагу для придания фигуркам плавности линий, выразительности, а также жесткости. Особенно актуален данный метод для таких негеометричных объектов, как фигурки животных и цветов - в этом случае они выглядят намного естественней и ближе к оригиналу

Бумага смачивается водой, от этого она становится более пластичной. В результате работы со смоченной бумагой получаются плавные формы. Изделия похожи на папье-маше.

Не всякая бумага подходит для мокрого складывания, а лишь та, в которую при производстве добавляют водорастворимый клей для скрепления волокон. Как правило, данным свойством обладают плотные сорта бумаги.

2.3 Модульное Оригами

Одной из популярных разновидностей оригами является модульное оригами, в котором целая фигура собирается из многих одинаковых частей (модулей).

Каждый модуль складывается по правилам классического оригами из одного листа бумаги, а затем модули соединяются путём вкладывания их друг в друга, появляющаяся при этом сила трения не даёт конструкции распасться.

Одним из наиболее часто встречающихся объектов модульного оригами является кусудама, объёмное тело шарообразной формы, собранное из бумажных цветов. Основой кусудамы, как правило, является какой-либо правильный многогранник (чаще всего куб, додекаэдр или икосаэдр). Несколько реже за основу берётся полуправильный многогранник.

2.4 Складывание по развёртке

Развёртка (англ. creasepattern; паттерн складок) — один из видов диаграмм оригами, представляющий собой чертёж, на котором изображены все складки готовой модели.

Складывание по развёртке сложнее складывания по традиционной схеме, однако, данный метод даёт не просто информацию, как сложить модель, но и как она была придумана — дело в том, что развёртки используются при разработке новых моделей оригами. Последнее также делает очевидным факт отсутствия для некоторых моделей иных диаграмм, кроме развёртки.

2.5 Наноригами

Сложная разновидность оригами. Это трёхмерный конструктор с малюсенькими элементами. Принципы наноригами используются в нанотехнологиях.

Фигуры в оригами выполняются из геометрических фигур: квадрата, треугольника, прямоугольника, пяти-, шести-, восьмиугольников, и даже круга.

То есть все фигуры в оригами выполняются из геометрических фигур, значит это одна из точек прикосновения оригами с математикой.

2.6 Киригами

Вид работы с бумагой при помощи ножниц. Ножницы дают большую свободу действий и более чёткие формы.

3. Оригами – это математика

Многие считают, что оригами это забава, с помощью которой люди создают различные фигуры, но очень многое в оригами связано с математикой. Оригами связано с геометрией, оригами, как наука, способна изумить нас формами, о возможности существования которых, мы, может быть, и не догадывались.

В процессе складывания фигур оригами мы знакомимся с различными геометрическими фигурами: треугольником, квадратом, трапецией и т.д., учимся легко ориентироваться в пространстве и на листе бумаги, делить целое на части, находить вертикаль, горизонталь, диагональ, узнаём многое другое, что относится к геометрии и математике. Американский педагог Ф. Фребель уже в середине XIX века заметил геометрическую особенность оригами и ввел его как учебный предмет в школе.

Первые попытки использовать оригами в педагогической практике в Европе справедливо связывают с именем немецкого гуманиста Фридриха Вильгельма Августа Фребеля (1792-1852).Именно он в начале XIX века начал создавать детские сады, а затем и школу. Фребель считал Природу лучшим учителем. Он сам сначала был лесником, очень любил и ценил природу и поэтому не хотел, чтобы в школе дети занимались зубрёжкой.

Например, основы геометрии он предлагал изучать не с помощью циркуля, линейки и некоторых понятий, а на примере фигур складывающейся бумаги. Он активно внедрял оригами в педагогический процесс.

Идеи Фребеля и сегодня очень интересны. Не удивительно поэтому, что в наши дни оригами продолжает играть определённую роль в развитии и воспитании. Оригами способствует активности, как левого, так и правого полушарий мозга, так как требует одновременного контроля за движениями обеих рук.

В конце XX века возник новый термин «оригаметрия», обозначающий область геометрии, в которой задачи решаются только методом складывания.

В наше время оригами с математической точностью шагает по планете семимильными шагами. Ученные придумали использовать приёмы оригами в космосе, а именно Миура-ори — схема жесткого складывания, которая использовалась для развертывания больших установок солнечных батарей на космических спутниках.

В ходе изучения геометрии с использованием оригами знакомимся с основными геометрическими фигурами (треугольник, прямоугольник, квадрат, ромб, четырехугольник), понятиями (сторона, угол, вершина угла, диагональ, центр фигуры), их свойствами и учимся основам техники оригами.

Работа по схемам, процесс складывания плоскостных фигур направлены на развитие восприятия, которое связано с различными операциями мышления.

По мнению дизайнера оригами Адзума Хидэаки, если развернуть фигуру оригами и посмотреть на складки – то можно увидеть лишь обилие многоугольников, соединенных друг с другом. В сложенном же виде оригами представляет собой многогранник, фигуру с множеством плоских поверхностей, а когда фигура разложена и показаны все складки, то мы можем увидеть множество геометрических фигур.

С точки зрения математики оригами, это точное определение местоположения одной или более точек листа, задающих складки, необходимые для формирования окончательного объекта. Сам же процесс складывания подразумевает выполнение последовательности точно определенных действий по следующим правилам, которые перекликаются с законами математики:

- точность выполнения инструкции;

- точки определяются пересечениями линий;

- линия определяется либо краем листа, либо линией сгиба бумаги;

- все линии прямые и делятся на два вида параллельные и перпендикулярные.

Математика это одна из сторон оригами и наоборот оригами является одной из направляющих математики.

Оригами в математике

Сумма углов треугольника равна 180 градусам. Возьмем произвольный треугольник ABC и перегнем лист в точке В перпендикулярно АС. Получим высоту ВН. Совместим вершины треугольника с точкой Н. Сумма углов А, B и С при наложении равна развернутому углу АНС, следовательно, равна 180 градусов.

Накрест лежащие углы при двух параллельных прямых и секущей равны. Возьмем лист бумаги, противолежащие стороны которого параллельны, а прямая АВ пересекает их. Сравним накрест лежащие углы 1 и 2. Согнем лист по секущей АВ, чтобы эти углы лежали в одной полуплоскости. Совместим вершины углов. Углы при наложении совпадают, что говорит об их равенстве.

Построение правильного треугольника. Возьмем квадрат АВСD. Согнем его пополам, правую и левую стороны также согнем пополам. Вершины А и В сгибаем к точкам, лежащим на срединном отрезке правой и левой частей, при этом линия сгиба должна выходить из центра стороны АВ. Согнем нижний край бумаги. Мы получили правильный треугольник. Проверить это можно наложением сторон друг на друга.

Разделение прямого угла на три равные части. Возьмем квадрат АВСD, разделим его пополам. Cовместим вершину D с линией сгиба так, чтобы вершина получившегося угла совпадала с точкой А. Перегнем оставшуюся часть листа по лучу АD. Вернем квадрат в исходное положение. Мы получили три равных угла. Проверить это можно наложением углов друг на друга.

Катет в прямоугольном треугольнике, лежащий против угла в 30 градусов, равен половине гипотенузы. Возьмем треугольник АВС, с углом С равным 90 градусов и углом А равным 30 градусов. Совместим сторону ВС с частью стороны АВ. Точка С перейдет в точку, которую мы назовем точкой Н. получили равные отрезки ВС и ВН (они совпали при наложении). Линия сгиба является биссектрисой угла В, назовем ее ВМ. Если полученный треугольник АМВ перегнуть по линии МН, то отрезки ВН и АН совпадут. Таким образом, сторона ВС в два раза меньше стороны АВ.

4. Взаимосвязь основ оригами и математики.

«Великий квадрат, не имеет пределов

Попробуй простую фигурку сложить,

И вмиг привлечёт интересное дело…»

А.Е.Гандаенко

Большинство классических моделей в оригами выполняются из квадрата. В процессе изготовления простых моделей мы знакомимся с очень нужными понятиями.

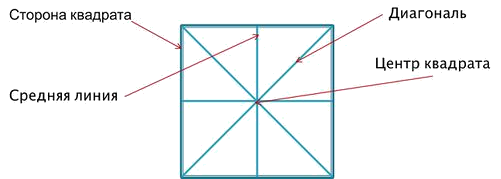
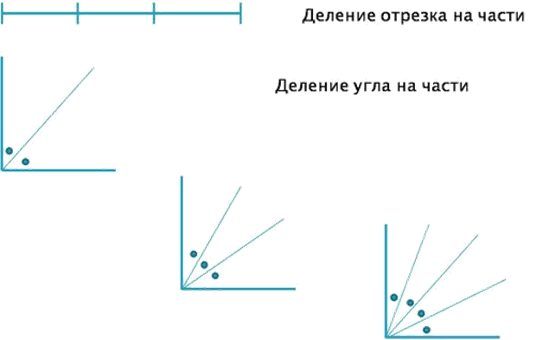
Деление на части является основами раздела математики – геометрии!!!

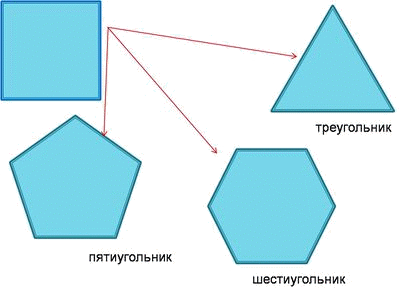
С помощью сгибов из квадрата можно получить другие правильные многоугольники.

С помощью оригами решаются геометрические задачи на плоскости. Значит оригами действительно связано с математикой. Продолжая исследование, складывая модульные конструкции, я пришла к выводу, что они напоминают геометрические тела. И я погрузилась в оригаметрию! Оригаметрия – раздел, который связывает искусство оригами с математикой.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Сгиб “долиной”

Сгиб “горкой”

Нахождение центра (без использования предметов для измерения)

Получение треугольника без линейки.

Деление листа бумаги формата А4 на 16 равных частей , без использования линейки и карандаша

Изготовление объемной фигуры

ЗАКЛЮЧЕНИЕ.

«Чтобы познать искусство оригами

И лучше геометрию постичь,

К фантазиям и знаниям прибавь ты

Огромное желание творить!

Терпение, старанье, аккуратность

К работе постоянно прилагай

И добрые чудесные решенья

В прекрасном настроенье создавай!»

По результатам моего исследования можно сделать вывод, что гипотеза подтвердилась – искусство оригами тесно связано с математикой и может стать хорошей основой для её изучения. Занимаясь оригами, я познакомилась на практике с элементами геометрии на плоскости и в пространстве и думаю мне это обязательно пригодится.

Я научилась изготавливать различные поделки используя технику оригами, узнала что существуют прямые и перпендикулярные линии,

А также я выяснила, что в оригами, как в и в математике, важна точность. Стоит отмерить лишние миллиметры, тут же меняется фигура и не получается то, что должно было получиться.

Приложение 1

Приложение 2

Кукла Катасиро

Приложение 3

Приложение 4

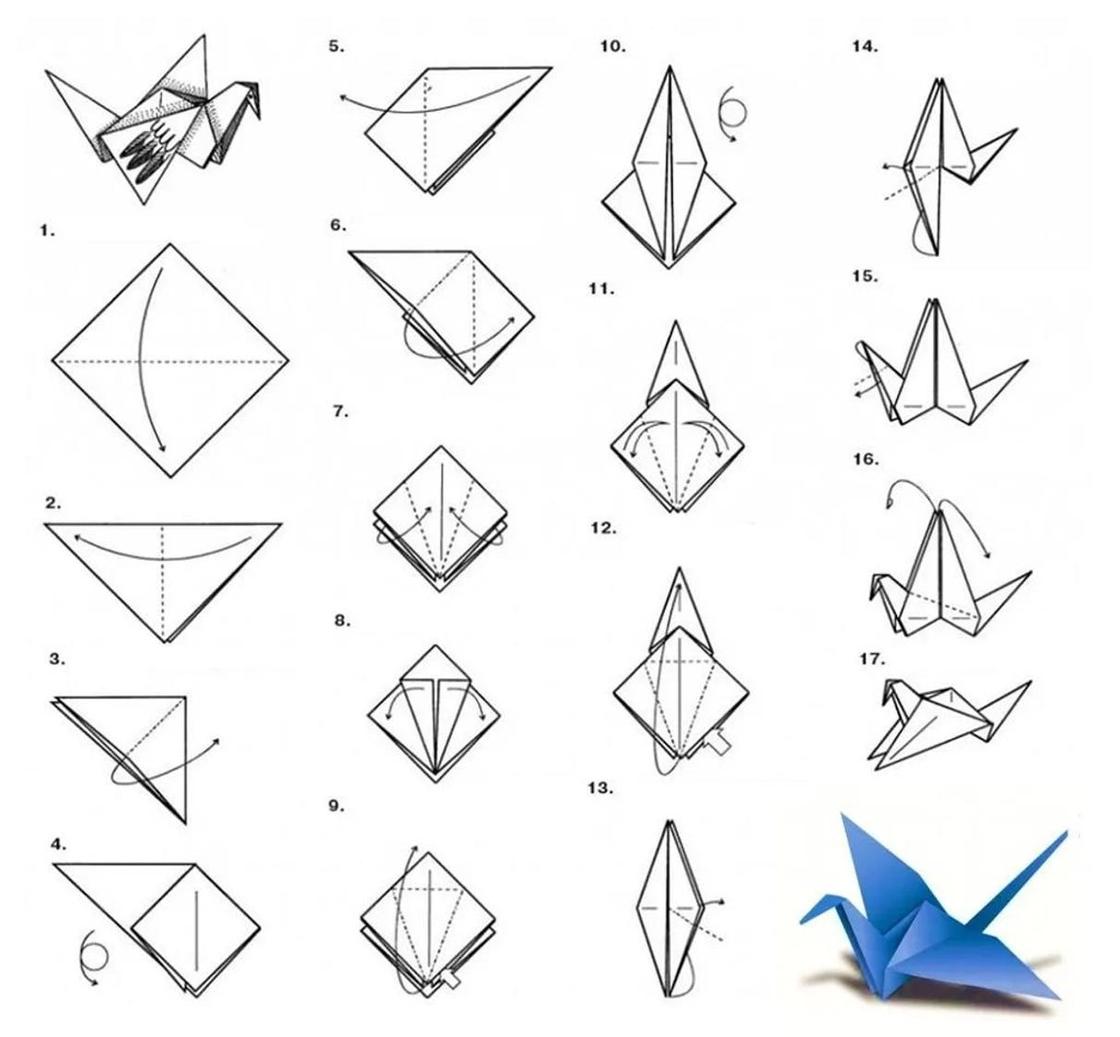
Журавль Цуру (схема изготовления)

Приложение 5

В 1990 году памятник Садако установлен в Парке Мира в Сиэтле (США), в 1995 - Детская статуя Мира в Санта-Фе (США, штат Нью-Мексико - в этом штате была сделана бомба, сброшенная на Хиросиму; статуя в Санта-Фе - "сестра" Детского мемориала в Хиросиме), в том же году открыт Сад Мира имени Садако в Санта-Барбаре с камнем, на котором выгравирован.

Приложение 6

Сгиб “долиной”

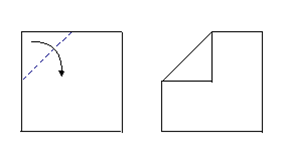
Сгиб “горой ”

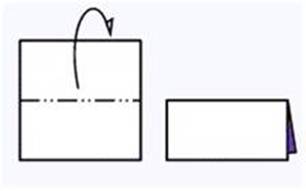
Сгиб “согнуть, разогнуть”

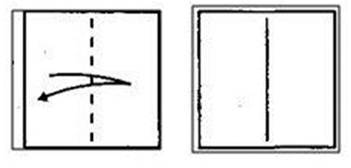
Повернуть в одной плоскости

Существующая линия сгиба

Линия сгиба “долиной”

Линия сгиба “горой”

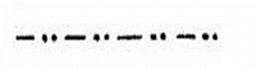
Список литературы

1. Модульное оригами: складываем объемные игрушки / Елена Образцова. – М.: Эксмо, 2014. – 64 с.: ил. – (Азбука рукоделия).

2. Интернет – источники:

• http://jorigami.ru/NewDoc/History_of_origami.htm

• https://docs.google.com/viewerng/viewer?url=http://nsportal.ru/sites/default/files/2012/07/25/issledovatelskiy_proekt_modulnoe_origami_i_matematika.pptx

• http://infourok.ru/proekt_modulnoe_origami_i_matematika-360271.htm

• http://www.youtube.com/watch?v=1u69h2Uk-Jw

• http://pedsovet.org/component/option,com_mtree/task,viewlink/link_id,111141/Itemid,118/

• https://ru.wikipedia.org/wiki

• http://www.zonar.info/node/10

• http://www.myshared.ru/slide/1002151/

3. Такахаси Коки «Оригами – это математика!»

4.     О. В. Весновская. Оригами: орнаменты,  кусудамы,  многогранники. -Чеб.:  изд. «Руссика», 2003г.

4.     С. Н. Белим. Задачи по геометрии, решаемые методами оригами. – М.: изд. «Аким», 1998г.,