Пояснительная записка
Структура программы
Программа включает четыре раздела:
Пояснительная записка, в которой конкретизируются общие цели основного общего образования по алгебре, даётся характеристика учебного курса, его место в учебном плане, приводятся личностные, метапредметные и предметные результаты освоения учебного курса, планируемые результаты изучения учебного курса.
Содержание курса алгебры 7 класса.
Примерное тематическое планирование с определением основных видов учебной деятельности обучающихся.
Рекомендации по организации и оснащению учебного процесса.
Распределение материала по темам.
Примерное тематическое планирование.
Система оценивания
Перечень контрольных работ.
Общая характеристика программы
Программа по математике составлена на основе программы Математика: 5 – 11 классы / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е.В.Буцко – М.: Вентана-граф, 2012. – 112 с.
Данная программа ориентирована на учебно-методический комплект «Алгебра. 7 класс» авторов А.Г. Мерзляка, В.Б. Полонского, М.С. Якира. Программа рассчитана на 3 часов в неделю, всего 102 часов (34 недели) и соответствует федеральному государственному образовательному стандарту основного общего образования.
Программа по алгебре составлена на основе Фундаментального ядра содержания общего образования, требований к результатам освоения образовательной программы основного общего образования, представленных в федеральном государственном образовательном стандарте основного общего образования, с учётом преемственности с примерными программами для начального общего образования по математике. В ней также учитываются доминирующие идеи и положения программы развития и формирования универсальных учебных действий для основного общего образования, которые обеспечивают формирование российской гражданской идентичности, коммуникативных качеств личности и способствуют формированию ключевой компетенции — умения учиться.
Курс алгебры 7-9 классов является базовым для математического образования и развития школьников. Алгебраические знания и умения необходимы для изучения геометрии в 7-9 классах, алгебры и математического анализа в 10-11 классах, а также изучения смежных дисциплин.
Практическая значимость школьного курса алгебры 7 - 9 классов состоит в том, что предметом его изучения являются количественные отношения и процессы реального мира, описанные математическими моделями. В современном обществе математическая подготовка необходима каждому человеку, так как математика присутствует во всех сферах человеческой деятельности.
Одной из основных целей изучения алгебры является развитие мышления, прежде всего формирование абстрактного мышления. В процессе изучения алгебры формируется логическое и алгоритмическое мышление, а также такие качества мышления, как сила и гибкость, конструктивность и критичность. Для адаптации в современном информационном обществе важным фактором является формирование математического стиля мышления, включающего в себя индукцию и дедукцию, обобщение и конкретизацию, анализ и синтез, классификацию и систематизацию, абстрагирование и аналогию.
Обучение алгебре даёт возможность школьникам научиться планировать свою деятельность, критически оценивать её, принимать самостоятельные решения, отстаивать свои взгляды и убеждения.
В процессе изучения алгебры школьники учатся излагать свои мысли ясно и исчерпывающе, приобретают навыки чёткого и грамотного выполнения математических записей, при этом использование математического языка позволяет развивать у учащихся грамотную устную и письменную речь.
Знакомство с историей развития алгебры как науки формирует у учащихся представления об алгебре как части общечеловеческой культуры.
Значительное внимание в изложении теоретического материала курса уделяется его мотивации, раскрытию сути основных понятий, идей, методов. Обучение построено на базе теории развивающего обучения, что достигается особенностями изложения теоретического материала и упражнениями на сравнение, анализ, выделение главного, установление связей, классификацию, обобщение и систематизацию. Особо акцентируются содержательное раскрытие математических понятий, толкование сущности математических методов и области их применения, демонстрация возможностей применения теоретических знаний для решения разнообразных задач прикладного характера, например решения текстовых задач, денежных и процентных расчётов, умение пользоваться количественной информацией, представленной в различных формах, умение читать графики. Осознание общего, существенного является основной базой для решения упражнений. Важно приводить детальные пояснения к решению типовых упражнений. Этим раскрывается суть метода, подхода, предлагается алгоритм или эвристическая схема решения упражнений определённого типа.
Геометрия – один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Геометрия является одним из опорных школьных предметов. Геометрические знания и умения необходимы для изучения других школьных дисциплин (физика, география, химия, информатика и др.).
Одной из основных целей изучения геометрии является развитие мышления, прежде всего формирование абстрактного мышления. В процессе изучения геометрии формируются логическое и алгоритмическое мышление, а также такие качества мышления, как сила и гибкость, конструктивность и критичность.
Обучение геометрии даёт возможность школьникам научиться планировать свою деятельность, критически оценивать её, принимать самостоятельные решения, отстаивать свои взгляды и убеждения.
В процессе изучения геометрии школьники учатся излагать свои мысли ясно и исчерпывающе, приобретают навыки чёткого выполнения математических записей, при этом использование математического языка позволяет развивать у учащихся грамотную устную и письменную речь.
Знакомство с историей развития геометрии как науки формирует у учащихся представления о геометрии как части общечеловеческой культуры.
Значительное внимание в изложении теоретического материала курса уделяется его мотивации, раскрытию сути основных понятий, идей, методов. Обучение построено на базе теории развивающего обучения, что достигается особенностями изложения теоретического материала и упражнениями на сравнение, анализ, выделение главного, установление связей, классификацию, доказательство, обобщение и систематизацию.
Общая характеристика курса алгебры в 7 классе:
Содержание курса алгебры в 7 классе представлено в виде следующих содержательных разделов:«Алгебра» и «Функции».
Содержание раздела «Алгебра» формирует знания о математическом языке, необходимые для решения математических задач, задач из смежных дисциплин, а также практических задач. Изучение материала способствует формированию у учащихся математического аппарата решения уравнений и их систем, текстовых задач с помощью уравнений и систем уравнений.
Материал данного раздела представлен в аспекте, способствующем формированию у учащихся умения пользоваться алгоритмами. Существенная роль при этом отводится развитию алгоритмического мышления — важной составляющей интеллектуального развития человека.
Содержание раздела «Числовые множества» нацелено на математическое развитие учащихся, формирование у них умения точно, сжато и ясно излагать мысли в устной и письменной речи. Материал раздела развивает понятие о числе, которое связано с изучением действительных чисел.
Цель содержания раздела «Функции» — получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования процессов и явлений окружающего мира. Соответствующий материал способствует развитию воображения и творческих способностей учащихся, умению использовать различные языки математики (словесный, символический, графический).
Личностные, метапредметные и предметные результаты освоения содержания курса алгебры:
Изучение алгебры по данной программе способствует формированию у учащихся личностных, метапредметных и предметных результатов обучения, соответствующих требованиям федерального государственного образовательного стандарта основного общего образования.
Личностные результаты:
воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;
ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;
умение контролировать процесс и результат учебной и математической деятельности;
критичность мышления, инициатива, находчивость, активность при решении математических задач.
Метапредметные результаты:
умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе, развивать мотивы и интересы своей познавательной деятельности;
умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
развитие компетентности в области использования ин- формационно-коммуникационных технологий;
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических задач, и представлять её в понятной форме, принимать решение в условиях неполной или избыточной, точной или вероятностной информации;
умение понимать и использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Предметные результаты:
осознание значения математики для повседневной жизни человека;
представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации;
развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования;
владение базовым понятийным аппаратом по основным разделам содержания;
систематические знания о функциях и их свойствах;
практически значимые математические умения и навыки, их применение к решению математических и нематематических задач предполагающее умения:
выполнять вычисления с действительными числами;
решать уравнения, неравенства, системы уравнений и неравенств;
решать текстовые задачи арифметическим способом, с помощью составления и решения уравнений, систем уравнений и неравенств;
использовать алгебраический язык для описания предметов окружающего мира и создания соответствующих математических моделей;
проверить практические расчёты: вычисления с процентами, вычисления с числовыми последовательностями, вычисления статистических характеристик, выполнение приближённых вычислений;
выполнять тождественные преобразования рациональных выражений;
выполнять операции над множествами;
исследовать функции и строить их графики;
читать и использовать информацию, представленную в виде таблицы, диаграммы (столбчатой или круговой);
решать простейшие комбинаторные задачи.
Общая характеристика курса геометрии в 7 классе
Содержание курса геометрии в 7 классе представлено в виде следующих содержательных разделов: «Простейшие геометрические фигуры и их свойства», «Треугольники»,
« Параллельные прямые. Сумма углов треугольника», «Окружность и круг. Геометрические построения».
Содержание раздела «Геометрические фигуры» служит базой для дальнейшего изучения учащимися геометрии. Изучение материала способствует формированию у учащихся знаний о геометрической фигуре как важнейшей математической модели для описания реального мира. Главная цель данного раздела – развить у учащихся воображение и логическое мышление путем систематического изучения свойств геометрических фигур и применения этих свойств длярешении задач вычислительного и конструктивного характера. Существенная роль при этом отводится развитию геометрической интуиции. Сочетание наглядности с формально- логическим подходом является неотъемлемой частью геометрических знаний.
Содержание раздела «Измерение геометрических величин» расширяет и углубляет представления учащихся об измерениях длин и углов, способствует формированию практических навыков, необходимых как при решении геометрических задач, так и в повседневной жизни.
Содержание раздела «Треугольники» даёт представление учащимся о том, что признаки равенства треугольников являются основным рабочим аппаратом всего курса геометрии. Доказательство большей части теорем курса и также решение многих задач проводится по следующей схеме: поиск равных треугольников – обоснование их равенства с помощью какого-то признака – следствия, вытекающие из равенства треугольников. Применение признаков равенства треугольников при решении задач дает возможность постепенно накапливать опыт проведения доказательных рассуждений. На начальном этапе изучения и применения признаков равенства треугольников целесообразно использовать задачи с готовыми чертежами.
При изучении раздела «Параллельные прямые. Сумма углов треугольника» учащиеся знакомятся с признаками и свойствами параллельных прямых, связанные с углами, образованными при пересечении двух прямых секущей (накрест лежащими, односторонними, соответственными). Содержание этого раздела широко используется в дальнейшем при изучении четырехугольников, подобных треугольников, при решении задач, а также в курсе стереометрии. В данной теме доказывается одна из важнейших теорем геометрии – теорема о сумме углов треугольника. Она позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный), а также установить некоторые свойства и признаки равенства прямоугольных треугольников. Понятие расстояния между параллельными прямыми вводится на основе доказанной предварительно теореме о том, что все точки каждой из двух параллельных прямых равноудалены от другой прямой. Это понятие играет важную роль, в частности используется в задачах на построение.
При изучении раздела «Окружность и круг. Геометрические построения» учащиеся учатся решать основные задачи на построение: построение угла, равного данному; построение серединного перпендикуляра данного отрезка; построение прямой, проходящей через данную точку и перпендикулярной данной прямой; построение биссектрисы данного угла; построение треугольника по двум сторонам и углу между ними; по стороне и двум прилежащим к ней углам; решать задачи на вычисление, доказательство и построение; строить треугольник по трём сторонам. При решении задач на построение в 7 классе следует ограничиться только выполнением и описанием построения искомой фигуры. В отдельных случаях можно провести устно анализ и доказательство, а элементы исследования должны присутствовать лишь тогда, когда это оговорено условием задачи.
Место курса алгебры в учебном плане
Базисный учебный (образовательный) план на изучение алгебры в 7 классе основной школы отводит 3 учебных часа в неделю в течение года обучения 35 недели, всего 105 часа.
Место курса геометрии в учебном плане
Базисный учебный (образовательный план) на изучение геометрии в 7 классе основной школе отводит 2 учебных часа в неделю в течение 35 недель обучения, всего 70 уроков (учебных занятий).
Планируемые результаты обучения алгебре в 7 классе
Алгебраические выражения
Учащийся научится:
оперировать понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные, работать с формулами;
выполнять преобразование выражений, содержащих степени с натуральными показателями;
выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами;
выполнять разложение многочленов на множители.
Учащийся получит возможность:
выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;
применять тождественные преобразования для решения задач из различных разделов курса.
Уравнения
Учащийся научится:
решать линейные уравнения с одной переменной, системы двух уравнений с двумя переменными;
понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.
Учащийся получит возможность:
овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
Функции
Учащийся научится:
• понимать и использовать функциональные понятия, язык (термины, символические обозначения);
строить графики линейной функций, исследовать свойства числовых функций на основе изучения поведения их графиков;
понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами;
Учащийся получит возможность:
проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; н основе графиков изученных функций строить боле сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
использовать функциональные представления и свойства функций для решения математических задач израз личных разделов курса.
В результате изучения курса геометрии в 7 классе ученик:
научится:
распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры (точка, прямая, отрезок, луч, угол, треугольник, окружность, шар, сфера, параллелепипед, пирамида и др.);
распознавать виды углов, виды треугольников;
определять по чертежу фигуры её параметры (длина отрезка, градусная мера угла, элементы треугольника, периметр треугольника и т.д.);
распознавать развертки куба, прямоугольного параллелепипеда, правильной пирамиды, цилиндра и конуса;
пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения;
распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;
находить значения длин линейных элементов фигур и их отношения, градусную меру углов от 00 до 1800, применяя определения, свойства и признаки фигур и их элементов, отношения фигур (равенство, сравнение);
решать задачи на доказательство, опираясь на изученные свойства фигур и отношений между ними и применяя изученные методы доказательств;
решать простейшие задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки;
решать простейшие планиметрические задачи в пространстве.
получит возможность использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
углубления и развития представлений о плоских и пространственных геометрических фигурах (точка, прямая, отрезок, луч, угол, треугольник, окружность, шар, сфера, параллелепипед, призма и др.);
применения понятия развертки для выполнения практических расчетов;
овладения методами решения задач на вычисления и доказательства: методом от противного, методом перебора вариантов;
приобретения опыта применения алгебраического аппарата при решении геометрических задач;
овладения традиционной схемой решения задач на построение с помощью циркуля и линейки: анализ, построение, доказательство и исследование;
приобретения опыта исследования свойств планиметрических фигур с помощью компьютерных программ.
Содержание курса алгебры 7 класса
Алгебраические выражения
Выражение с переменными. Значение выражения с переменными. Допустимые значения переменных. Тождества. Тождественные преобразования алгебраических выражений. Доказательство тождеств.
Степень с натуральным показателем и её свойства. Одночлены. Одночлен стандартного вида. Степень одночлена Многочлены. Многочлен стандартного вида. Степень многочлена. Сложение, вычитание и умножение многочленов Формулы сокращённого умножения: квадрат суммы и квадрат разности двух выражений, произведение разности суммы двух выражений. Разложение многочлена на множители. Вынесение общего множителя за скобки. Метод группировки. Разность квадратов двух выражений. Сумм и разность кубов двух выражений.
Уравнения
Уравнение с одной переменной. Корень уравнения. Равносильные уравнения. Свойства уравнений с одной переменной. Уравнение как математическая модель реальной ситуации.
Линейное уравнение. Рациональные уравнения. Решение рациональных уравнений, сводящихся к линейным. Решение текстовых задач с помощью рациональных уравнений.
Уравнение с двумя переменными. График уравнения с двумя переменными. Линейное уравнение с двумя переменными и его график.
Системы уравнений с двумя переменными. Графический метод решения системы уравнений с двумя переменными. Решение систем уравнений методом подстановки и сложения. Система двух уравнений с двумя переменными как модель реальной ситуации.
Функции
Числовые функции
Функциональные зависимости между величинами. Понятие функции. Функция как математическая модель реального процесса. Область определения и область значения функции. Способы задания функции. График функции.
Линейная функция, ее свойства и графики.
Распределение материала по темам:
.
| № главы | ТЕМА | Кол-во часов по программе |
| I. | Линейное уравнение с одной переменной. | 15 |
| II. | Целые выражения. | 53 |
| III. | Функции. | 12 |
| IV. | Системы линейных уравнений с двумя переменными. | 18 |
|
| Повторение и систематизация учебного материала. | 8 |
|
| Всего: | 105 |
Содержание курса геометрия 7 класс.
Простейшие геометрические фигуры и их свойства. (13 час.)
Точки и прямые. Отрезок и его длина Луч. Угол. Измерение углов. Смежные и вертикальные углы. Перпендикулярные прямые. Аксиомы.
Треугольники. (18 час.)
Равные треугольники. Высота, медиана, биссектриса треугольника. Первый и второй признаки равенства треугольников Равнобедренный треугольник и его свойства. Признаки равнобедренного треугольника. Третий признак равенства треугольников. Теоремы.
Параллельные прямые. Сумма углов треугольника. (16 час.)
Параллельные прямые. Признаки параллельных прямых. Свойства параллельных прямых. Сумма углов треугольника. Прямоугольный треугольник. Свойства прямоугольного треугольника.
Окружность и круг. Геометрические построения. (16 час.)
Геометрическое место точек. Окружность и круг. Некоторые свойства окружности. Касательная к окружности. Описанная и вписанная окружности треугольника. Задачи на построение. Метод геометрических мест точек в задачах на построение.
Повторение (7 час.)
Распределение материала по темам:
| № главы | Тема | Кол-во часов по программе |
| I. | Простейшие геометрические фигуры и их свойства. | 12 |
| II. | Треугольники. | 20 |
| III. | Параллельные прямые. Сумма углов треугольника. | 15 |
| IV. | Окружность и круг. Геометрические построения. | 17 |
|
| Повторение курса геометрии за 7 класс | 6 |
|
| Всего: | 70 |
Тематическое планирование.
3 часа в неделю, всего 105 часов;
| № раздела и урока | Тема урока, раздела | Количество часов | Дата по плану | Дата по факту | Планируемые результаты | Характеристика деятельности обучающихся
|
Корректировка планиро вания для детей с ОВЗ |
| Личностные (Л) | Метапредметные (код) | Предметные |
|
|
| Ученик научиться | Ученик получит возможность научиться |
|
|
| Глава 1. Линейное уравнение с одной переменной. (14 часов) |
|
| 1/1 | Введение в алгебру. | 3 |
|
| Л.1,2 | П.2,6,7 Р.1,5 К.4 | 1)решать линейные уравнения с одной переменной; 2)понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций. | 1)овладеть специальными приёмами решения уравнений; 2)уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
| Распознавать числовые выражения и выражения с переменными, линейные уравнения. Приводить примеры выражений с переменными, линейных уравнений. Составлять выражение с переменными по условию задачи. Выполнять преобразования выражений: приводить подобные слагаемые, раскрывать скобки. Находить значение выражения с переменными при заданных значениях переменных. Классифицировать алгебраические выражения. Описывать целые выражения. Формулировать определение линейного уравнения. Решать линейное уравнение в общем виде. Интерпретировать уравнение как математическую модель реальной ситуации. Описывать схему решения текстовой задачи, применять её для решения задач. | уметь находить взаимосвязь математики и действительности - владеть навыками самоконтроля - уметь критически оценивать результат. - развивать общие интеллектуальные умения: работа по алгоритму
|
| 1/2 | Введение в алгебру. |
|
|
| 1/3 | Введение в алгебру. |
|
|
| 1/4 | Линейное уравнение с одной переменной. | 5 |
|
| Л.3,4 | П.8 Р.3,8,11 К.6 |
| 1/5 | Линейное уравнение с одной переменной. |
|
|
| 1/6 | Линейное уравнение с одной переменной. |
|
|
| 1/7 | Линейное уравнение с одной переменной. |
|
|
| 1/8 | Линейное уравнение с одной переменной. |
|
|
| 1/9 | Решение задач с помощью уравнений. | 5 |
|
| Л.4,6,9 | П.1,2 Р.5 К.4 |
| 1/10 | Решение задач с помощью уравнений. |
|
|
| 1/11 | Решение задач с помощью уравнений. |
|
|
| 1/12 | Решение задач с помощью уравнений. |
|
|
| 1/13 | Решение задач с помощью уравнений. |
|
|
| 1/14 | Контрольная работа № 1 «Линейные уравнения с одной переменной». | 1 |
|
|
|
|
|
|
|
|
| Глава 2. Целые выражения. (53 часа) |
|
| 2/1 | Тождественноравные выражения. Тождества. | 2 |
|
| Л.2 | Р.11,12 К.4 | 1)оперировать понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные, работать с формулами; 2)выполнять преобразование выражений, содержащих степени с натуральными показателями; 3)выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами; 4)выполнять разложение многочленов на множители. | 1)выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов; 2)применять тождественные преобразования для решения задач из различных разделов курса.
| Формулировать: определения: тождественно равных выражений, тождества, степени с натуральным показателем, одночлена, стандартного вида одночлена, коэффициента одночлена, степени одночлена, многочлена, степени многочлена; свойства: степени с натуральным показателем, знака степени; правила: доказательства тождеств, умножения одночлена на многочлен, умножения многочленов. Доказывать свойства степени с натуральным показателем. Записывать и доказывать формулы: произведения суммы и разности двух выражений, разности квадратов двух выражений, квадрата суммы и квадрата разности двух выражений, суммы кубов и разности кубов двух выражений. Вычислять значение выражений с переменными. Применять свойства степени для преобразования выражений. Выполнять умножение одночленов и возведение одночлена в степень. Приводить одночлен к стандартному виду. Записывать многочлен в стандартном виде, определять степень многочлена. Преобразовывать произведение одночлена и многочлена; суммы, разности, произведения двух многочленов в многочлен. Выполнять разложение многочлена на множители способом вынесения общего множителя за скобки, способом группировки, по формулам сокращённого умножения и с применением нескольких способов. Использовать указанные преобразования в процессе решения уравнений, доказательства утверждений, решения текстовых задач. | Находить значения числовых выражений, а также выражений с переменными при указанных значениях переменных. Использовать знаки , ах=в при различных значениях а и в, а также несложные уравнения, сводящиеся к ним. Использовать аппарат уравнений для решения текстовых задач, интерпретировать результат. Использовать простейшие статистические характеристики (среднее арифметическое, размах, мода, медиана) для анализа ряда данных в несложных ситуациях |
| 2/2 | Тождественноравные выражения. Тождества. |
|
|
| 2/3 | Степеньс натуральнымпоказателем. | 3 |
|
| Л.3 | П.1,12 К.3 |
| 2/4 | Степеньс натуральнымпоказателем. |
|
|
| 2/5 | Степеньс натуральнымпоказателем. |
|
|
| 2/6 | Свойства степени с натуральным показателем. | 3 |
|
| Л.7 | П.13,15 К.6 |
| 2/7 | Свойства степени с натуральным показателем. |
|
|
| 2/8 | Свойства степени с натуральным показателем. |
|
|
| 2/9 | Одночлены. | 2 |
|
| Л.1,7 | П.19 К.4 | Вычислять значения выражений вида an ,где а-произвольное число, n – натуральное число, устно и письменно, а также с помощью калькулятора. Формулировать, записывать в символической форме и обосновывать свойства степени с натуральным показателем. Применять свойства степени для преобразования выражений. Выполнять умножение одночленов и возведение одночленов в степень. Строить графики функций y=x2 и y=x3
|
| 2/10 | Одночлены. |
|
|
| 2/11 | Многочлены. | 2 |
|
| Л.1,9 | П.3 К.4 |
| 2/12 | Многочлены. |
|
|
| 2/13 | Сложение и вычитание многочленов. | 3 |
|
| Л.2,3 | П.7,8 Р.7 К.1 |
| 2/14 | Сложение и вычитание многочленов. |
|
|
| 2/15 | Сложение и вычитание многочленов. |
|
|
| 2/16 | Контрольная работа № 2 «Сложение и вычитание многочленов». | 1 |
|
|
|
|
| 2/17 | Умножениеодночленана многочлен. | 4 |
|
| Л.5 | П.7,8 Р.9 К.1 | Записывать многочлен в стандартном виде, определять степень многочлена. Выполнять сложение и вычитание многочленов, умножение одночлена на многочлен и многочлена на многочлен. Выполнять разложение многочлена на множители, используя вынесение множителя за скобки и способ группировки. Применять действия с многочленами при решении разнообразных задач, в частности при решении текстовых задач с помощью уравнений |
| 2/18 | Умножениеодночленана многочлен. |
|
|
| 2/19 | Умножениеодночленана многочлен. |
|
|
| 2/20 | Умножениеодночленана многочлен. |
|
|
| 2/21 | Умножение многочлена на многочлен. | 4 |
|
| Л.5 | П.7,8 Р.11,12
|
| 2/22 | Умножение многочлена на многочлен. |
|
|
| 2/23 | Умножение многочлена на многочлен. |
|
|
| 2/24 | Умножение многочлена на многочлен. |
|
|
| 2/25 | Разложение многочленов на множители. Вынесение общего множителя за скобки. | 3 |
|
| Л.2,9 | П.15 Р.12 К.4 |
| 2/26 | Разложение многочленов на множители. Вынесение общего множителя за скобки. |
|
|
| 2/27 | Разложение многочленов на множители. Вынесение общего множителя за скобки. |
|
|
| 2/28 | Разложение многочленов на множители. Метод группировки. | 3 |
|
| Л.7 | П.15 К.3 |
| 2/29 | Разложение многочленов на множители. Метод группировки. |
|
|
| 2/30 | Разложение многочленов на множители. Метод группировки. |
|
|
| 2/31 | Контрольная работа № 3 «Умножение одночленов и многочленов» | 1 |
|
|
|
|
| 2/32 | Произведение разности и суммы двух выражений. | 3 |
|
| Л.5,8 | П.14 Р.10 К.1 |
| 2/33 | Произведение разности и суммы двух выражений. |
|
|
| 2/34 | Произведение разности и суммы двух выражений. |
|
|
| 2/35 | Разность квадратов двух выражений. | 2 |
|
| Л.5 | П.16 Р.8
|
| 2/36 | Разность квадратов двух выражений. |
|
|
| 2/37 | Квадрат суммы и квадрат разности двух выражений. | 4 |
|
| Л.3,5 | Р.3,4 К.2 |
| 2/38 | Квадрат суммы и квадрат разности двух выражений. |
|
|
| 2/39 | Квадрат суммы и квадрат разности двух выражений. |
|
|
| 2/40 | Квадрат суммы и квадрат разности двух выражений. |
|
|
| 2/41 | Преобразование многочлена в квадрат суммы или разности двух выражений. | 3 |
|
| Л.3 | П.1,4
|
| 2/42 | Преобразование многочлена в квадрат суммы или разности двух выражений. |
|
|
| 2/43 | Преобразование многочлена в квадрат суммы или разности двух выражений. |
|
|
| 2/44 | Контрольная работа № 4 «Формулы сокращенного умножения». | 1 |
|
|
|
|
| 2/45 | Сумма и разность кубов двух выражений. | 2 |
|
| Л.1 | П.3,6 Р.5 | Знать формулы сокращённого умножения, применять их в преобразованиях целых выражений в многочлены, а также для разложения многочленов на множители. Использовать различные преобразования целых выражений при решении уравнений, доказательстве тождеств, в задачах на делимость, в вычислении значений некоторых выражений с помощью калькулятора |
| 2/46 | Сумма и разность кубов двух выражений. |
|
|
| 2/47 | Применение различных способов разложения многочлена на множители. | 6 |
|
| Л.5,7 | П.1,3,5 Р.7 К.6 |
| 2/48 | Применение различных способов разложения многочлена на множители. |
|
|
| 2/49 | Применение различных способов разложения многочлена на множители. |
|
|
| 2/50 | Применение различных способов разложения многочлена на множители. |
|
|
| 2/51 | Применение различных способов разложения многочлена на множители. |
|
|
| 2/52 | Применение различных способов разложения многочлена на множители. |
|
|
| 2/53 | Контрольная работа № 5 «Применение формул сокращенного умножения». | 1 |
|
|
|
|
|
|
|
| Глава 3. Функции. (12 часов) |
|
| 3/1 | Связи между величинами. Функция. | 2 |
|
|
| П.2,7 Р.8 К.4 | 1)понимать и использовать функциональные понятия, язык (термины, символические обозначения); 2)строить графики линейной функций, исследовать свойства числовых функций на основе изучения поведения их графиков; 3)понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами. | 1)проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; н основе графиков изученных функций строить боле сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.); 2)использовать функциональные представления и свойства функций для решения математических задач израз личных разделов курса. | Приводить примеры зависимостей между величинами. Различать среди зависимостей функциональные зависимости. Описывать понятия: зависимой и независимой переменных, функции, аргумента функции; способы задания функции. Формулировать определения: области определения функции, области значений функции, графика функции, линейной функции, прямой пропорциональности. Вычислять значение функции по заданному значению аргумента. Составлять таблицы значений функции. Строить график функции, заданной таблично. По графику функции, являющейся моделью реального процесса, определять характеристики этого процесса. Строить график линейной функции и прямой пропорциональности. Описывать свойства этих функций. | Вычислять значения функции, заданной формулой, составлять таблицы значений функции. По графику функции находить значение функции по известному значению аргумента и решать обратную задачу. Строить графики прямой пропорциональности и линейной функции, описывать свойства этих функций. Понимать как влияет знак углового коэффициента на расположение в координатной плоскости графика функции y=kx,k≠0, как зависит от значений k и b взаимное расположение графиков двух функций вида y=kx+b, иллюстрировать это на компьютере. Интерпретировать графики реальных зависимостей, описываемых формулами вида y=kx, k≠0 и y=kx+b |
| 3/2 | Связи между величинами. Функция. |
|
|
| 3/3 | Способы задания функции. | 2 |
|
| Л.3,9 | П.13 К.3 |
| 3/4 | Способы задания функции. |
|
|
| 3/5 | График функции. | 3 |
|
|
| П.3 Р.3 К.6 |
| 3/6 | График функции. |
|
|
| 3/7 | График функции. |
|
|
| 3/8 | Линейная функция, её график и свойства. | 4 |
|
| Л.1,7 | П.3,5 Р.9 |
| 3/9 | Линейная функция, её график и свойства. |
|
|
| 3/10 | Линейная функция, её график и свойства. |
|
|
| 3/11 | Линейная функция, её график и свойства. |
|
|
| 3/12 | Контрольнаяработа № 6 «Функции». | 1 |
|
|
|
|
|
|
|
|
| Глава 4. Системы линейных уравнений с двумя переменными. (18 часов) |
|
| 4/1 | Уравнения с двумя переменными. | 2 |
|
| Л.3,7 | П.1,3 Р.2 К.4 | 1)решать системы двух уравнений с двумя переменными; 2)понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом; 3)применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.
| 1)овладеть специальными приёмами решения уравнений с двумя переменными и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики; 2)применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
| Приводить примеры: уравнения с двумя переменными; линейного уравнения с двумя переменными; системы двух линейных уравнений с двумя переменными; реальных процессов, для которых уравнение с двумя переменными или система уравнений с двумя переменными являются математическими моделями. Определять, является ли пара чисел решением данного уравнения с двумя переменными. Формулировать: определения: решения уравнения с двумя переменными; что значит решить уравнение с двумя переменными; графика уравнения с двумя переменными; линейного уравнения с двумя переменными; решения системы уравнений с двумя переменными; свойства уравнений с двумя переменными. Описывать: свойства графика линейного уравнения в зависимости от значений коэффициентов, графический метод решения системы двух уравнений с двумя переменными, метод подстановки и метод сложения для решения системы двух линейных уравнений с двумя переменными. Строить график линейного уравнения с двумя переменными. Решать системы двух линейных уравнений с двумя переменными. Решать текстовые задачи, в которых система двух линейных уравнений с двумя переменными является математической моделью реального процесса, и интерпретировать результат решения системы. | Определять, является ли пара чисел решением данного уравнения с двумя переменными. Находить путём перебора целые решения линейного уравнения с двумя переменными. Строить график уравнения ax+by=c, где a≠0 или b≠0. Решать графическим способом системы линейных уравнений с двумя переменными. Применять способ подстановки и способ сложения при решении систем линейных уравнений с двумя переменными. Решать текстовые задачи, используя в качестве алгебраической модели систему уравнений. |
| 4/2 | Уравнения с двумя переменными. |
|
|
| 4/3 | Линейное уравнение с двумя переменными и его график. | 3 |
|
| Л.5 | П.18 Р.8 К.3 |
| 4/4 | Линейное уравнение с двумя переменными и его график. |
|
|
| 4/5 | Линейное уравнение с двумя переменными и его график. |
|
|
| 4/6 | Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными. | 3 |
|
| Л.5,9 | П.7,18 Р.3
|
| 4/7 | Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными. |
|
|
| 4/8 | Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными. |
|
|
|
| 4/9 | Решение систем линейных уравнений методом подстановки. | 2 |
|
| Л.1,3 | П.2 Р.9 К.3 |
| 4/10 | Решение систем линейных уравнений методом подстановки. |
|
|
| 4/11 | Решение систем линейных уравнений методом сложения. | 3 |
|
| Л.1,9 | П.2,9 Р.10,11 К.4 |
| 4/12 | Решение систем линейных уравнений методом сложения. |
|
|
| 4/13 | Решение систем линейных уравнений методом сложения. |
|
|
| 4/14 | Решение задач с помощью систем линейных уравнений. | 4 |
|
| Л.3,9 | П.1,5 Р.1,5 К.1 |
| 4/15 | Решение задач с помощью систем линейных уравнений. |
|
|
| 4/16 | Решение задач с помощью систем линейных уравнений. |
|
|
| 4/17 | Решение задач с помощью систем линейных уравнений. |
|
|
| 4/18 | Контрольная работа № 7 «Системы линейных уравнений с двумя неизвестными». | 1 |
|
|
|
|
|
| Повторение и систематизация учебного материала. (8 часов) |
|
|
| Упражнения для повторения курса 7 класса. | 7 |
|
|
| К.2,5 |
|
|
|
|
|
| Итоговая контрольнаяработа. | 1 |
|
|
|
|
|
|
|
|
| 1. Готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию; 2. Первичнаясформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками; 3. Умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, приводить примеры и контрпримеры; 4. Первоначальное представление о математической науке как сфере человеческой деятельности; 5. Критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта; 6. Креативность мышления, инициативы, находчивости, активность при решении арифметических задач; 7. умение контролировать процесс и результат учебной математической деятельности; 8. формирование способности к эмоциональному восприятию математических задач, решений, рассуждений; 9. формирование аккуратности и терпеливости. | 1. Использование знаково-символьных средств; 2. Осуществлять анализ объектов с выделением существенных признаков; 3. Формирование умения обобщать, составлять алгоритм математических действий; 4. Моделирование; 5. Выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; 6. Действие самоконтроля и самооценки процесса и результата деятельности; 7. Построение логической цепи рассуждений; 8. Поиск и выделение необходимой информации; 9. Синтез – составление целого из частей; 10. Структурирование знаний; 11. Контроль и оценка процесса и результата товарищеской деятельности; 12. Формулирование проблемы; 13. Самостоятельный поиск решения; 14. Выбор оснований для сравнения; 15. Выдвижение гипотез и их обоснование; 16. Анализ объектов с целью выделения признаков; 17. Установление причинно-следственных связей; 18. Личностное, профессиональное, жизненное самоопределение; 19. Рефлексия способов действия.
| 1. Прогнозирование результата; 2. Планирование своих действий в соответствии с поставленной задачей; 3. Работа по алгоритму; 4. Целеполагание, как постановка учебной задачи; 5. Планирование, определение последовательности действий; 6. Оценка, выделение и осознание учащимися того, что уже усвоено и того, что еще нужно усвоить; 7. Осознание качества и уровня усвоения; 8. Коррекция; 9. Самостоятельность в оценивании правильность действий и внесение необходимые коррективы в исполнение действий; 10. Планирование учебного сотрудничества; 11. Постановка цели; 12. Формировать способность адекватно оценивать правильность или ошибочность выполнения поставленной задачи, ее объективную трудность и собственные возможности ее решения. | 1. Осуществлениевзаимного контроля; 2. Управлять поведением партнера – контроль, коррекция, оценка его действий; 3. Постановка вопросов – инициативное сотрудничество в поиске и сборе информации; 4. Умение точно выражать свои мысли в соответствии с задачами коммуникации; 5. Инициативное сотрудничество в группе; 6. Планирование учебного сотрудничества.
|
Тематическое планирование.
2 часа в неделю, всего 68 часов;
| № раздела и урока | Тема урока, раздела | Количество часов | Дата по плану | Дата по факту | Планируемые результаты | Характеристика деятельности обучающихся
|
Корректировка планиро вания для детей с ОВЗ |
| Личностные (Л) | Метапредметные (код) | Предметные |
| Ученик научиться | Ученик получит возможность научиться |
| Глава 1. Простейшие геометрические фигуры и их свойства. (12 часов) |
|
| 1/1 | Точки и прямые. | 1 |
|
| Л.3 | П.1,4 К.3 | 1)распознавать на чертежах, рисунках, моделях и в окружающем мире плоские геометрические фигуры (точка, прямая, отрезок, луч, угол; 2)распознавать виды углов; 3)определять по чертежу фигуры её параметры (длина отрезка, градусная мера угла; 4)пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения; 5)распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации; 6)находить значения длин линейных элементов фигур и их отношения, градусную меру углов от 00 до 1800, применяя определения, свойства и признаки фигур и их элементов, отношения фигур (равенство, сравнение). | 1)углубления и развития представлений о плоских геометрических фигурах (точка, прямая, отрезок, луч, угол.
| Приводить примеры геометрических фигур. Описывать точку, прямую, отрезок, луч, угол. Формулироватьопределения ииллюстрироватьпонятия: отрезка, луча; равных отрезков, середины отрезка, расстояния между двумя точками, дополнительных лучей; угла, прямого, острого, тупого и развёрнутого угла, равных углов, биссектрисы угла, смежных и вертикальных углов; пересекающихся прямых, перпендикулярных прямых, перпендикуляра, наклонной, расстояния от точки до прямой;свойства: расположения точек на прямой, измерения отрезков и углов, смежных и вертикальных углов, перпендикулярных прямых; основное свойство прямой. Доказывать:теоремы о пересекающихся прямых, о свойствах смежных и вертикальных углов, о единственности прямой, перпендикулярной данной (случай, когда точка лежит на данной прямой). Находитьдлину отрезка, градусную меру угла, используя свойства их измерений. Изображать с помощью чертёжных инструментов геометрические фигуры: отрезок, луч, угол, смежные и вертикальные углы, перпендикулярные прямые, отрезки и лучи. Пояснять, что такое аксиома, определение. Решать задачи на вычисление и доказательство, проводя необходимые доказательные рассуждения. | Объяснять, что такое отрезок, луч, угол, какие фигуры называются равными, как сравниваются и измеряются отрезки и углы, что такое градус и градусная мера угла, какой угол называется тупым, прямым, развёрнутым, что такое середина отрезка и биссектриса угла, какие углы называются смежными и какие вертикальными; формулировать и обосновывать утверждения о свойствах смежных и вертикальных углов; объяснять, какие прямые называются перпендикулярными; формулировать и обосновывать утверждение о свойстве двух прямых, перпендикулярных к третьей; изображать и распознавать указанные простейшие фигуры на чертежах; решать задачи, связанные с этими простейшими фигурами. |
| 1/2 | Отрезок и его длина. | 2 |
|
| Л.4 | П.6,9 Р.4 |
| 1/3 | Отрезок и его длина. |
|
|
| 1/4 | Луч и угол. | 3 |
|
| Л.7 | П.1,12 Р.11 К.4 |
| 1/5 | Измерение углов. |
|
|
| 1/6 | Луч и угол. Измерение углов. |
|
|
| 1/7 | Смежные углы. | 3 |
|
| Л.6,9 | П.6,7 Р.6 К.1 |
| 1/8 | Вертикальные углы. |
|
|
| 1/9 | Смежные и вертикальные углы. |
|
|
| 1/10 | Перпендикулярные прямые. | 1 |
|
|
| П.2 |
| 1/11 | Аксиомы. | 1 |
|
|
| П.2 |
| 1/12 | Контрольная работа №1 «Простейшие геометрические фигуры и их свойства». | 1 |
|
|
|
|
|
| Глава 2. Треугольники. (20 часов) |
|
| 2/1 | Равные треугольники. | 3 |
|
| Л.1,3 | П.2,4 Р.4 К.3 | 1)распознавать виды треугольников; 2)определять по чертежу фигуры её параметры (элементы треугольника, периметр треугольника и т.д.); 3)распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации; 4)находить значения длин линейных элементов фигур и их отношения, применяя определения, свойства и признаки фигур и их элементов, отношения фигур (равенство, сравнение); 5)решать задачи на доказательство, опираясь на изученные свойства фигур и отношений между ними и применяя изученные методы доказательств.
| 1)углубления и развития представлений о плоских геометрических фигурах (треугольник); 2)овладения методами решения задач на вычисления и доказательства: методом от противного, методом перебора вариантов.
| Описывать смысл понятия «равные фигуры». Приводить примеры равных фигур. Распознавать и изображать на чертежах и рисунках равносторонние, равнобедренные, прямоугольные, остроугольные, тупоугольные треугольники и их элементы. Классифицировать треугольники по сторонам и углам. Формулировать:определения:остроугольного, тупоугольного, прямоугольного, равнобедренного, равностороннего, разностороннего треугольников; биссектрисы, высоты, медианы треугольника; равных треугольников; серединного перпендикуляра; периметра треугольника; свойства: равнобедренного треугольника, серединного перпендикуляра отрезка, основного свойства равенства треугольников; признаки: равенства треугольников, равнобедренного треугольника. Доказыватьтеоремы: о единственности прямой, перпендикулярной данной (случай, когда точка лежит вне данной прямой); три признака равенства треугольников; признаки равнобедренного треугольника; теоремы о свойствах серединного перпендикуляра, равнобедренного и равностороннего треугольников. Разъяснять, что такое теорема, описывать структуру теоремы. Объяснять, какую теорему называют обратной данной, в чём заключается метод доказательства от противного. Приводить примеры использования этого метода. Решать задачи на вычисление и доказательство. | Объяснять, какая фигура называется треугольником, что такое вершины, стороны, углы и периметр треугольника, какой треугольник называется равнобедренным и какой равносторонним, какие треугольники называются равными; изображать и распознавать на чертежах треугольники и их элементы; формулировать теоремы о признаках равенства треугольников; объяснять, что называется перпендикуляром, проведённым из данной точки к данной прямой; формулировать теорему о перпендикуляре к прямой; объяснять, какие отрезки называются медианой, биссектрисой и высотой треугольника; формулировать теоремы о свойствах равнобедренного треугольника; решать задачи, связанные с признаками равенства треугольников и свойствами равнобедренного треугольника; формулировать определение окружности; объяснять, что такое центр, радиус, хорда и диаметр окружности; решать простейшие задачи на построение (построение угла, равного данному, построение биссектрисы угла, построение перпендикулярных прямых, построение середины отрезка) |
| 2/2 | Высота, медиана, биссектриса треугольника. |
|
|
| 2/3 | Равные треугольники. Высота, медиана, биссектриса треугольника. |
|
|
| 2/4 | Первый признак равенства треугольников. | 6 |
|
| Л.4
| П.5,10 Р.8,9 |
| 2/5 | Первый признак равенства треугольников. |
|
|
| 2/6 | Второй признак равенства треугольников. |
|
|
| 2/7 | Второй признак равенства треугольников. |
|
|
| 2/8 | Решение задач. |
|
|
| 2/9 | Решение задач. |
|
|
| 2/10 | Контрольная работа №2 «Первый и второй признаки равенства треугольников». | 1 |
|
|
|
|
|
| 2/11 | Равнобедренный треугольник и его свойства. | 4 |
|
| Л.5 | П.3,6 Р.9 К.2 |
|
| 2/12 | Равнобедренный треугольник и его свойства. |
|
|
| 2/13 | Равнобедренный треугольник и его свойства. |
|
|
| 2/14 | Равнобедренный треугольник и его свойства. |
|
|
| 2/15 | Признаки равнобедренного треугольника. | 2 |
|
| Л.8 | П.18 Р.12 К.6 |
| 2/16 | Признаки равнобедренного треугольника. |
|
|
| 2/17 | Третий признак равенства треугольников. | 2 |
|
|
| П.2 Р.2 К.5 |
| 2/18 | Третий признак равенства треугольников. |
|
|
| 2/19 | Теоремы. | 1 |
|
| Л.8,9 | К.3,4 |
| 2/20 | Контрольная работа №3 «Равнобедренный треугольник». | 1 |
|
|
|
|
|
| Глава3. Параллельные прямые. Сумма углов треугольника. (15 часов) |
|
| 3/1 | Параллельные прямые. | 1 |
|
| Л.2 | П.3 | 1)пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения; 2)распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации; 3)решать задачи на доказательство, опираясь на изученные свойства фигур и отношений между ними и применяя изученные методы доказательств. | 1)овладения методами решения задач на вычисления и доказательства: методом от противного, методом перебора вариантов; 2)приобретения опыта применения алгебраического аппарата при решении геометрических задач; 3)овладения традиционной схемой решения задач на построение с помощью циркуля и линейки: анализ, построение, доказательство и исследование. | Распознавать на чертежах параллельные прямые. Изображать с помощью линейки и угольника параллельные прямые. Описыватьуглы, образованные при пересечении двух прямых секущей. Формулировать: определения: параллельных прямых, расстояния между параллельными прямыми, внешнего угла треугольника, гипотенузы и катета; свойства: параллельных прямых; углов, образованных при пересечении параллельных прямых секущей; суммы улов треугольника; внешнего угла треугольника; соотношений между сторонами и углами треугольника; прямоугольного треугольника; основное свойство параллельных прямых; признаки: параллельности прямых, равенства прямоугольных треугольников. Доказывать: теоремы о свойствах параллельных прямых, о сумме углов треугольника, о внешнем угле треугольника, неравенство треугольника, теоремы о сравнении сторон и углов треугольника, теоремы о свойствах прямоугольного треугольника, признаки параллельных прямых, равенства прямоугольных треугольников. Решатьзадачи на вычисление и доказательство. | Формулировать определение параллельных прямых; объяснять с помощью рисунка , какие углы образованные при пересечении двух прямых секущей, называются накрест лежащими, какие односторонними и какие соответственными; формулировать теоремы, выражающие признаки параллельности прямых; объяснять, что такое аксиомы; формулировать аксиому параллельных прямых и выводить следствия из неё; формулировать теоремы о свойствах параллельных прямых, обратные теоремам о признаках параллельности, связанных с накрест лежащими, соответственными и односторонними углами, в связи с этим объяснять, что такое условие и заключение теоремы, какая теорема называется обратной по отношению к данной теореме; объяснять, в чём заключается метод доказательства от противного: формулировать теоремы об углах с соответственно параллельными и перпендикулярными сторонами; решать задачи на вычисления, доказательство и построение, связанные с параллельными прямыми. |
| 3/2 | Признаки параллельности прямых. | 2 |
|
| Л.1 | Р.4 |
| 3/3 | Признаки параллельности прямых. |
|
|
| 3/4 | Свойства параллельных прямых. | 3 |
|
| Л.4 | П.2,19 Р.9 К.3 |
| 3/5 | Свойства параллельных прямых. |
|
|
| 3/6 | Свойства параллельных прямых. |
|
|
| 3/7 | Сумма углов треугольника. | 4 |
|
| Л.5 | П.4,5 Р.10 К.1 |
| 3/8 | Сумма углов треугольника. Внешний угол треугольника. |
|
|
| 3/9 | Сумма углов треугольника. Неравенство треугольника. |
|
|
| 3/10 | Сумма углов треугольника. |
|
|
| 3/11 | Прямоугольный треугольник. | 2 |
|
| Л.8 | К.6 |
| 3/12 | Прямоугольный треугольник. |
|
|
| 3/13 | Свойства прямоугольного треугольника. | 2 |
|
| Л.7 | П.9 Р.8 |
| 3/14 | Свойства прямоугольного треугольника. |
|
|
| 3/15 | Контрольная работа №4 «Параллельные прямые». |
|
|
|
|
|
|
| Глава 4.Окружность и круг. Геометрические построения. (17 часов) |
|
| 4/1 | Геометрическое место точек. Окружность и круг. | 2 |
|
| Л.2 | П.7,8 Р.4,9 К.3 | 1)распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры (окружность, шар, сфера, параллелепипед, пирамида и др.); 2)распознавать развертки куба, прямоугольного параллелепипеда, правильной пирамиды, цилиндра и конуса; 3)пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения; 4)распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации; 5)решать простейшие задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки; 6)решать простейшие планиметрические задачи в пространстве.
| 1)углубления и развития представлений о плоских и пространственных геометрических фигурах (окружность, шар, сфера, параллелепипед, призма и др.); 2)применения понятия развертки для выполнения практических расчетов; 3)овладения традиционной схемой решения задач на построение с помощью циркуля и линейки: анализ, построение, доказательство и исследование; 4)приобретения опыта исследования свойств планиметрических фигур с помощью компьютерных программ.
| Пояснять, что такое задача на построение; геометрическое место точек (ГМТ). Приводить примеры ГМТ. Изображать на рисунках окружность и её элементы; касательную к окружности; окружность, вписанную в треугольник, и окружность, описанную около него. Описывать взаимное расположение окружности и прямой. Формулировать: определения: окружности, круга, их элементов; касательной к окружности; окружности, описанной около треугольника, и окружности, вписанной в треугольник; свойства: серединного перпендикуляра как ГМТ; биссектрисы угла как ГМТ; касательной к окружности; диаметра и хорды; точки пересечения серединных перпендикуляров сторон треугольника; точки пересечения биссектрис углов треугольника; признакикасательной. Доказывать: теоремы о серединном перпендикуляре и биссектрисе угла как ГМТ;
о свойствах касательной; об окружности, вписанной в треугольник, описанной около треугольника; признаки касательной. Решать основные задачи на построение: построение угла, равного данному; построение серединного перпендикуляра данного отрезка; построение прямой, проходящей через данную точку и перпендикулярной данной прямой; построение биссектрисы данного угла; построение треугольника по двум сторонам и углу между ними; по стороне и двум прилежащим к ней углам.Решать задачи на построение методом ГМТ. Строить треугольник по трём сторонам. Решать задачи на построение, доказательство и вычисление. Выделять в условии задачи условие и заключение. Опираясь на условие задачи, проводить необходимые доказательные рассуждения. Сопоставлять полученный результат с условием задачи. |
|
| 4/2 | Геометрическое место точек. Окружность и круг. |
|
|
| 4/3 | Некоторые свойства окружности. Касательная к окружности. | 3 |
|
| Л.4 | П.1,13 Р.6,8 |
| 4/4 | Некоторые свойства окружности. Касательная к окружности. |
|
|
| 4/5 | Некоторые свойства окружности. Касательная к окружности. |
|
|
| 4/6 | Описанная и вписанная окружности треугольника. | 3 |
|
| Л.6,9 | Р.11 К.4 |
| 4/7 | Описанная и вписанная окружности треугольника. |
|
|
| 4/8 | Описанная и вписанная окружности треугольника. |
|
|
| 4/9 | Задачи на построение. | 4 |
|
| Л.8 | П.2,3 К.6 |
| 4/10 | Задачи на построение. |
|
|
| 4/11 | Задачи на построение. |
|
|
| 4/12 | Задачи на построение. |
|
|
| 4/13 | Метод геометрических мест точек в задачах на построение. | 4 |
|
| Л.1,3 | П.4,8 Р.12 К.2 |
| 4/14 | Метод геометрических мест точек в задачах на построение. |
|
|
|
| 4/15 | Метод геометрических мест точек в задачах на построение. |
|
|
| 4/16 | Метод геометрических мест точек в задачах на построение. |
|
|
| 4/17 | Контрольная работа №5 «Окружность и круг». | 1 |
|
|
|
|
|
| Обобщение и систематизация знаний учащихся. (6 часа) |
|
|
| Упражнения для повторения курса 7 класса. | 5 |
|
|
|
|
|
|
|
|
|
| Итоговая контрольная работа №6. | 1 |
|
|
|
|
|
|
|
|
Система оценки планируемых результатов
Для оценки планируемых результатов данной программой предусмотрено использование:
вопросов и заданий для самостоятельной подготовки;
заданий для подготовки к итоговой аттестации;
тестовых задания для самоконтроля;
Виды контроля и результатов обучения
Текущий контроль
Тематический контроль
Итоговый контроль
Методы и формы организации контроля
Устный опрос.
Монологическая форма устного ответа.
Письменный опрос:
Математический диктант;
Самостоятельная работа;
Контрольная работа.
Особенности контроля и оценки по математике.
Текущий контроль осуществляется как в письменной, так и в устной форме при выполнении заданий в тетради.
Письменные работы можно проводить в виде тестовых или самостоятельных работ на бумаге Время работы в зависимости от сложности работы 5-10 или 15-20 минут урока. При этом возможно введение оценки «за общее впечатление от письменной работы» (аккуратность, эстетика, чистота, и т.д. ). Эта отметка дополнительная и в журнал выносится по желанию ребенка.
Итоговый контроль проводится в форме контрольных работ практического типа. В этих работах с начала отдельно оценивается выполнение каждого задания, а затем вводится итоговая отметка. При этом итоговая отметка является не средним баллом, а определяется с учетом тех видов заданий, которые для данной работы являются основными.
Оценка ответов учащихся
Оценка – это определение степени усвоения учащимися знаний, умений, навыков в соответствии с требованиями государственного образовательного стандарта.
1. Устный ответ оценивается отметкой «5», если учащийся:
– полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
– изложил материал грамотным языком в определенной логической последовательности, точно используя специальную терминологию и символику;
– правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
– показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
– продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;
– отвечал самостоятельно без наводящих вопросов учителя;
– возможны одна-две неточности при освещении второстепенных вопросов или в рисунках, чертежах и т.д., которые ученик легко исправил по замечанию учителя.
2. Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на отметку «5», но при этом имеет один из недостатков:
– в изложении допущены небольшие пробелы, не исказившие содержание ответа;
– допущены один-два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
– допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в рисунках, чертежах и т.д., легко исправленных по замечанию учителя.
3. Отметка «3» ставится в следующих случаях:
– неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала;
– имелись затруднения или допущены ошибки в определении понятий, использовании специальной терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
– учащийся не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
– при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Оценка контрольных и самостоятельных письменных работ.
Оценка "5" ставится, если ученик:
Оценка "4" ставится, если ученик выполнил работу полностью, но допустил в ней:
Оценка "3" ставится, если ученик правильно выполнил не менее половины работы или допустил:
или не более одной грубой и одной негрубой ошибки и одного недочета;
или не более двух-трех негрубых ошибок;
или одной негрубой ошибки и трех недочетов;
или при отсутствии ошибок, но при наличии четырех-пяти недочетов.
Критерии выставления оценок за проверочные тесты.
1. Критерии выставления оценок за тест
Время выполнения работы: на усмотрение учителя.
Оценка «5» - 100 – 90% правильных ответов, «4» - 70-90%, «3» - 50-70%, «2» - менее 50% правильных ответов.
В рабочей программе предусмотрено 8 контрольных работ:
Контрольная работа № 1 «Линейные уравнения с одной переменной».
Контрольная работа № 2 «Сложение и вычитание многочленов».
Контрольная работа № 3 «Умножение одночленов и многочленов».
Контрольная работа № 4 «Формулы сокращенного умножения».
Контрольная работа № 5 «Применение формул сокращенного умножения».
Контрольная работа № 6 «Функции.»
Контрольная работа № 7 «Системы линейных уравнений с двумя неизвестными».
Итоговая контрольная работа №8.
Рекомендации по оснащению учебного процесса
Оснащение процесса обучения алгебре обеспечивается библиотечным фондом печатными пособиями, а также информационно-коммуникативными средствами, экранно-звуковыми приборами, техническими средствами обучения, учебно-практическим и учебно-лабораторным оборудованием.
Библиотечный фонд
Нормативные документы:
Федеральный государственный образовательный стандарт основного общего образования.
Примерные программы основного общего образования. Математика. (Стандарты второго поколения.) — М.: Просвещение, 2010.
Формирование универсальных учебных действий в основной школе: система заданий / А.Г. Асмолов, О.А. Карабанова. — М.: Просвещение, 2010.
Учебно-методический комплект:
Алгебра: 7 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2012.
Алгебра: 7 класс: дидактические материалы: пособие для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович, М.С. Якир. — М.: Вентана-Граф, 2013.
Алгебра: 7 класс: методическое пособие / Е.В. Буцко, А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.:Вентана-Граф, 2013.
Справочные пособия, научно-популярная и историческая литература
Агаханов Н.Х., ПодлипскийO.K. Математика: районные олимпиады: 6-11 классы. — М.: Просвещение, 1990.
Гаврилова Т.Д. Занимательная математика: 5-11 классы. — Волгоград: Учитель, 2008.
Левитас Г.Г. Нестандартные задачи по математике. — М.: ИЛЕКСА, 2007.
Перли С.С., Перли Б.С. Страницы русской истории на уроках математики. — М.: Педагогика-Пресс, 1994.
Пичугин Л.Ф. За страницами учебника алгебры. — М.: Просвещение, 2010. ^
Пойа Дж. Как решать задачу? — М.: Просвещение, 1975,-
Произволов В.В. Задачи на вырост. — М.: МИРОС, 1995,
Фарков А.В. Математические олимпиады в школе : 5- 11 классы. — М. : Айрис-Пресс, 2005.
Энциклопедия для детей. Т. 11: Математика. — М.: Аванта-+, 2003.
http://www.kvant.info/ Научно-популярный физико-математический журнал для школьников и студентов «Квант».
Печатные пособия
Таблицы по алгебре для 7-9 классов.
Портреты выдающихся деятелей в области математики.
Информационные средства
Коллекция медиаресурсов, электронные базы данных.
Интернет.
Экранно-звуковые пособия
1.Видеофильмы об истории развития математики, математических идей и методов.
2.Алгебра .7 класс. Видеоуроки.
Технические средстваобучения
Компьютер.
Мультимедиапроектор.
Экран навесной.
Интерактивная доска.
Учебно-практическоеи учебно-лабораторное оборудование
Доска магнитная.
Комплект чертёжных инструментов (классных и раздаточных): линейка, транспортир, угольник (30°, 60°), угольник (45°, 45°), циркуль.
Наборы для моделирования (цветная бумага, картон, калька, клей, ножницы, пластилин).
Система оценки планируемых результатов
Для оценки планируемых результатов данной программой предусмотрено использование:
вопросов и заданий для самостоятельной подготовки;
заданий для подготовки к итоговой аттестации;
тестовых задания для самоконтроля;
Виды контроля и результатов обучения
Текущий контроль
Тематический контроль
Итоговый контроль
Методы и формы организации контроля
Устный опрос.
Монологическая форма устного ответа.
Письменный опрос:
Математический диктант;
Самостоятельная работа;
Контрольная работа.
Особенности контроля и оценки по математике.
Текущий контроль осуществляется как в письменной, так и в устной форме при выполнении заданий в тетради.
Письменные работы можно проводить в виде тестовых или самостоятельных работ на бумаге Время работы в зависимости от сложности работы 5-10 или 15-20 минут урока. При этом возможно введение оценки «за общее впечатление от письменной работы» (аккуратность, эстетика, чистота, и т.д. ). Эта отметка дополнительная и в журнал выносится по желанию ребенка.
Итоговый контроль проводится в форме контрольных работ практического типа. В этих работах с начала отдельно оценивается выполнение каждого задания, а затем вводится итоговая отметка. При этом итоговая отметка является не средним баллом, а определяется с учетом тех видов заданий, которые для данной работы являются основными.
Оценка ответов учащихся
Оценка – это определение степени усвоения учащимися знаний, умений, навыков в соответствии с требованиями государственного образовательного стандарта.
1. Устный ответ оценивается отметкой «5», если учащийся:
– полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
– изложил материал грамотным языком в определенной логической последовательности, точно используя специальную терминологию и символику;
– правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
– показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
– продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;
– отвечал самостоятельно без наводящих вопросов учителя;
– возможны одна-две неточности при освещении второстепенных вопросов или в рисунках, чертежах и т.д., которые ученик легко исправил по замечанию учителя.
2. Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на отметку «5», но при этом имеет один из недостатков:
– в изложении допущены небольшие пробелы, не исказившие содержание ответа;
– допущены один-два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
– допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в рисунках, чертежах и т.д., легко исправленных по замечанию учителя.
3. Отметка «3» ставится в следующих случаях:
– неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала;
– имелись затруднения или допущены ошибки в определении понятий, использовании специальной терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
– учащийся не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
– при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Оценка контрольных и самостоятельных письменных работ.
Оценка "5" ставится, если ученик:
Оценка "4" ставится, если ученик выполнил работу полностью, но допустил в ней:
Оценка "3" ставится, если ученик правильно выполнил не менее половины работы или допустил:
или не более одной грубой и одной негрубой ошибки и одного недочета;
или не более двух-трех негрубых ошибок;
или одной негрубой ошибки и трех недочетов;
или при отсутствии ошибок, но при наличии четырех-пяти недочетов.
Критерии выставления оценок за проверочные тесты.
1. Критерии выставления оценок за тест
Время выполнения работы: на усмотрение учителя.
Оценка «5» - 100 – 90% правильных ответов, «4» - 70-90%, «3» - 50-70%, «2» - менее 50% правильных ответов.
В рабочей программе предусмотрено 6 контрольных работ:
Контрольная работа № 1 «Простейшие геометрические фигуры и их свойства»
Контрольная работа № 2 «Первый и второй признаки равенства треугольников»
Контрольная работа № 3 «Равнобедренный треугольник»
Контрольная работа № 4 «Параллельные прямые»
Контрольная работа № 5 «Окружность и круг»
Итоговая контрольная работа №6.
Описание учебно-методического и материально-технического обеспечения образовательного процесса
| Наименование объектов и средств материально-технического обеспечения |
Примечания |
| Программы |
| Математика: программы: 5-9 классы /А.Г. Мерзляк, В. Б. Полонский, М. С. Якир, Е. В. Буцко. – 2 изд., дораб. – М.: Вентана-Граф, 2012. – 112 с. | В программе определены цели и задачи курса, рассмотрены особенности содержания и результаты его освоения (личностные, метапредметные и предметные); представлены содержание основного общего образования по математике, тематическое планирование с характеристикой основных видов деятельности учащихся, описано материально-техническое обеспечение образовательного процесса |
| Учебники |
| Мерзляк А.Г., Полонский В. Б., Якир М. С. Геометрия: 7 класс. Учебник. – М.: Вентана – Граф, 2014
| В учебниках реализована главная цель, которую ставили перед собой авторы – развитие личности школьника средствами математики, подготовка его к продолжению обучения и к самореализации в современном обществе. В учебниках представлен материал, соответствующий программе и позволяющий учащимся 5-9 классов выстраивать индивидуальные траектории изучения математики за счет обязательного и дополнительного материала, маркированной разноуровневой системы упражнений, организованной помощи в разделе «Ответы, советы и решения», дополнительного материала: различных практикумов, исследовательских и практических работ, домашних контрольных работ, исторического и справочного материала и др. |
| Дидактические материалы |
| Мерзляк А.Г., Полонский В. Б., Якир М. С. Геометрия: 7 класс. Дидактические материалы: сборник задач и контрольных работ. – М.: Вентана – Граф, 2014 Ершова А. П., Голобородько В.В. Алгебра. Геометрия. Самостоятельные и контрольные работы для 7 класса.- М.: Илекса, 2008. Ершова А.П. Сборник заданий для тематического и итогового контроля знаний. Геометрия. 7 класс – М.: Илекса, - 2013. | Дидактические материалы обеспечивают диагностику и контроль качества обучения в соответствии с требованиями к уровню подготовки учащихся, закрепленными в стандарте. Пособия содержат проверочные работы: тесты, самостоятельные и контрольные работы, дополняют задачный материал учебников и рабочих тетрадей, содержит ответы ко всем заданиям. |
| Компьютерные и информационно-коммуникативные средства обучения. |
| СD-ROM «Математика. 5-11 классы»
СD-ROM «Интерактивная математика». 5-9 классы.
| Мультимедийные обучающие программы носят проблемно-тематический характер и обеспечивают дополнительные условия для изучения отдельных тем и разделов математики. Диски разработаны для самостоятельной работы учащихся на уроках (если класс оснащен компьютерами) или в домашних условиях. Материал по основным вопросам математики основной школы представлен на дисках в трех аспектах: демонстрации по содержанию предмета, практикумы по решению задач, работы для самоконтроля уровня усвоения знаний. |
УУД.
| Личностные УУД (Л.) | Познавательные УУД (П.) | Регулятивные УУД (Р.) | Коммуникативные УУД (К.) |
| 1. Готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию; 2. Первичнаясформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками; 3. Умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, приводить примеры и контрпримеры; 4. Первоначальное представление о математической науке как сфере человеческой деятельности; 5. Критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта; 6. Креативность мышления, инициативы, находчивости, активность при решении арифметических задач; 7. умение контролировать процесс и результат учебной математической деятельности; 8. формирование способности к эмоциональному восприятию математических задач, решений, рассуждений; 9. формирование аккуратности и терпеливости. | 1. Использование знаково-символьных средств; 2. Осуществлять анализ объектов с выделением существенных признаков; 3. Формирование умения обобщать, составлять алгоритм математических действий; 4. Моделирование; 5. Выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; 6. Действие самоконтроля и самооценки процесса и результата деятельности; 7. Построение логической цепи рассуждений; 8. Поиск и выделение необходимой информации; 9. Синтез – составление целого из частей; 10. Структурирование знаний; 11. Контроль и оценка процесса и результата товарищеской деятельности; 12. Формулирование проблемы; 13. Самостоятельный поиск решения; 14. Выбор оснований для сравнения; 15. Выдвижение гипотез и их обоснование; 16. Анализ объектов с целью выделения признаков; 17. Установление причинно-следственных связей; 18. Личностное, профессиональное, жизненное самоопределение; 19. Рефлексия способов действия.
| 1. Прогнозирование результата; 2. Планирование своих действий в соответствии с поставленной задачей; 3. Работа по алгоритму; 4. Целеполагание, как постановка учебной задачи; 5. Планирование, определение последовательности действий; 6. Оценка, выделение и осознание учащимися того, что уже усвоено и того, что еще нужно усвоить; 7. Осознание качества и уровня усвоения; 8. Коррекция; 9. Самостоятельность в оценивании правильность действий и внесение необходимые коррективы в исполнение действий; 10. Планирование учебного сотрудничества; 11. Постановка цели; 12. Формировать способность адекватно оценивать правильность или ошибочность выполнения поставленной задачи, ее объективную трудность и собственные возможности ее решения. | 1. Осуществлениевзаимного контроля; 2. Управлять поведением партнера – контроль, коррекция, оценка его действий; 3. Постановка вопросов – инициативное сотрудничество в поиске и сборе информации; 4. Умение точно выражать свои мысли в соответствии с задачами коммуникации; 5. Инициативное сотрудничество в группе; 6. Планирование учебного сотрудничества.
|
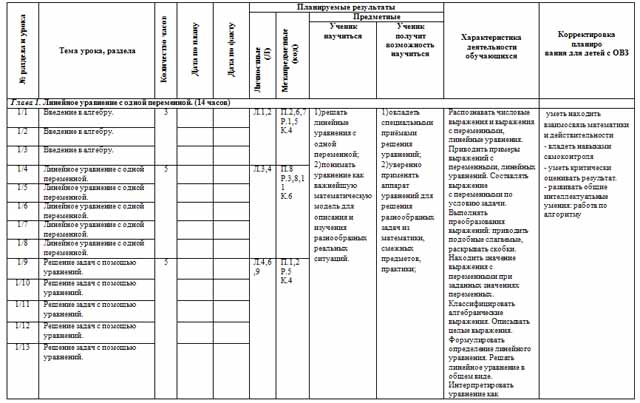

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по алгебре и геометрии для 7 класса (0.11 MB)
Рабочая программа по алгебре и геометрии для 7 класса (0.11 MB)
 0
0 562
562 35
35 Нравится
0
Нравится
0








