Ростовская область Мартыновский район х. Кривой Лиман пер. Южный,1
Муниципальное бюджетное общеобразовательное учреждение –
средняя общеобразовательная школа №22 х.Кривой Лиман
«Утверждаю»
Директор МБОУ- СОШ №22
Приказ от 29.08.2019г. № 230
Директор_________ Редько Г.А.
РАБОЧАЯ ПРОГРАММА
по _алгебре_на 2019-2020 учебный год
Уровень общего образования: основное общее образование 7 класс
Количество часов в год 101
Учитель: Манасян Алеся Николаевна
Программа разработана на основе:
-Федерального государственного общеобразовательного стандарта основного общего образования, утверждённого приказом Минобрнауки России от 17 декабря 2010 г. № 1897 « Об утверждении и введении в действие федерального государственного общеобразовательного стандарта основного общего образования»;
- Примерных рабочих программ. 7—9 классы: пособие для учителей общеобразовательных организаций / (сост.Т. А. Бурмистрова). — 2-е изд., дораб. — М.: Просвещение, 2016
- Основной образовательной программы МБОУ-СОШ №22 х. Кривой Лиман;
- ориентирована на учебник «Алгебра 7» автор Ю. Н. Макарычев. М. Просвещение. 2017.
Изменения и дополнения, внесённые в рабочую программу в течение учебного года.
| Основание (дата и номер приказа) | Дата |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Раздел I. Планируемые результаты
Личностные результаты освоения образовательной программы:
1) воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству; осознание своей этнической принадлежности, знание истории, языка, культуры своего народа на примере содержания текстовых задач;
2) формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, осознанному выбору и построению дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений, с учётом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к труду, развития опыта участия в социально значимом труде;
3) формирование осознанного, уважительного и доброжелательного отношения к другому человеку, его мнению, мировоззрению, культуре, языку, вере, гражданской позиции, к истории, культуре, религии, традициям; готовности и способности вести диалог с другими людьми и достигать в нём взаимопонимания;
4) освоение социальных норм, правил поведения, ролей и форм социальной жизни в группах и сообществах, включая взрослые и социальные сообщества; участие в школьном самоуправлении и общественной жизни в пределах возрастных компетенций;
5) развитие морального сознания и компетентности в решении моральных проблем на основе личностного выбора, формирование нравственных чувств и нравственного поведения, осознанного и ответственного отношения к собственным поступкам;
6) формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, детьми старшего и младшего возраста, взрослыми в процессе образовательной, общественно полезной, учебно-исследовательской, творческой и других видов деятельности;
7) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контр примеры;
8) первоначальное представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
9) критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
10) креативность мышления, инициатива, находчивость, активность при решении арифметических задач;
11) умение контролировать процесс и результат учебной математической деятельности;
12) формирование способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
13) формирование ценности здорового и безопасного образа жизни;
14) осознание значения семьи в жизни человека и общества, принятие ценности семейной жизни, уважительное и заботливое отношение к членам своей семьи через участие во внеклассной работе;
15) развитие эстетического сознания, творческой деятельности эстетического характера через выполнение творческих работ
Метапредметные результаты освоения образовательной программы:
1) умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности;
2) умение самостоятельно планировать пути достижения целей, в том числе альтернативные, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
3) умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
4) умение оценивать правильность выполнения учебной задачи, ее объективную трудность и собственные возможности её решения;
5) владение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности;
6) умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
7) умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач;
8) смысловое чтение;
9) умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; формулировать, аргументировать и отстаивать своё мнение;
10) умение осознанно использовать речевые средства в соответствии с задачей коммуникации для выражения своих чувств, мыслей и потребностей; планирования и регуляции своей деятельности; владение устной и письменной речью, монологической контекстной речью;
11) формирование и развитие компетентности в области использования информационно-коммуникационных технологий (далее ИКТ– компетенции);
12) первоначальное представление об идеях и методах математики как об универсальном языке науки и техники;
13) развитие способности видеть математическую задачу в других дисциплинах, в окружающей жизни;
14) умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
15) умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
16) умение выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
17) понимание сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
18) умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
19) способность планировать и осуществлять деятельность, направленную на решение задач исследовательского характера
Предметные результаты освоения образовательной программы:
Алгебраические выражения. Тождества
Ученик научится:
владеть понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами;
выполнять преобразования выражений, содержащих степени с целыми показателями;
выполнять разложение многочленов на множители.
Ученик получит возможность научиться выполнять многошаговые преобразования целых выражений, применяя широкий набор способов и приёмов;
Уравнения
Ученик научится:
решать основные виды линейных уравнений с одной переменной, системы двух уравнений с двумя переменными;
понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.
Ученик получит возможность:
овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
Функции
Учащийся научится:
понимать и использовать функциональные понятия и язык (термины, символические обозначения);
строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;
понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Учащийся получит возможность научиться:
проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса.
Описательная статистика
Учащийся научится использовать простейшие способы представления и анализа статистических данных.
Учащийся получит возможность приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы.
Комбинаторика
Учащийся научится решать комбинаторные задачи на нахождение числа объектов или комбинаций.
Учащийся получит возможность научиться некоторыми специальным приемам решения комбинаторных задач
Раздел II. Содержание учебного предмета
Отбор содержания обучения осуществляется на основе следующих дидактических принципов: систематизация знаний; соответствие обязательному минимуму содержания образования в основной школе; усиление общекультурной направленности материала; учет психолого-педагогических особенностей, актуальных для возрастного периода; создание условий для понимания и осознания воспринимаемого материала.
| Тема | Элементы содержания |
| Повторение |
|
| Глава 1. Выражения. Тождества. Уравнения. | Числовые выражения, выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений. Статистические характеристики. Основная цель — систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной. Первая тема курса 7 класса является связующим звеном между курсом математики 5—6 классов и курсом алгебры. В ней закрепляются вычислительные навыки, систематизируются и обобщаются сведения о преобразованиях выражений и решении уравнений. Нахождение значений числовых и буквенных выражений дает возможность повторить с учащимися правила действий с рациональными числами. Умения выполнять арифметические действия с рациональными числами являются опорными для всего курса алгебры. Следует выяснить, насколько прочно овладели ими учащиеся, и в случае необходимости организовать повторение с целью ликвидации выявленных пробелов. Развитию навыков вычислений должно уделяться серьезное внимание и в дальнейшем при изучении других тем курса алгебры. В связи с рассмотрением вопроса о сравнении значений выражений расширяются сведения о неравенствах: вводятся знаки неравенств, дается понятие о двойных неравенствах. При рассмотрении преобразований выражений формально-оперативные умения остаются на том же уровне, учащиеся поднимаются на новую ступень в овладении теорией. Вводятся понятия «тождественно равные выражения», «тождество», «тождественное преобразование выражений», содержание которых будет постоянно раскрываться и углубляться при изучении преобразований различных алгебраических выражений. Подчеркивается, что основу тождественных преобразований составляют свойства действий над числами. Усиливается роль теоретических сведений при рассмотрении уравнений. С целью обеспечения осознанного восприятия учащимися алгоритмов решения уравнений вводится вспомогательное понятие равносильности уравнений, формулируются и разъясняются на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней. В системе упражнений особое внимание уделяется решению уравнений вида ах = b при различных значениях а и b. Продолжается работа по формированию у учащихся умения использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остается таким же, как в 6 классе. Изучение темы завершается ознакомлением учащихся с простейшими статистическими характеристиками: средним арифметическим, модой, медианой, размахом. Учащиеся должны уметь использовать эти характеристики для анализа ряда данных в несложных ситуациях. |
| Глава 2. Функции | Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и ее график. Основная цель — ознакомить учащихся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида. Данная тема является начальным этапом в систематической функциональной подготовке учащихся. Здесь вводятся такие понятия, как функция, аргумент, область определения функции, график функции. Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представление о способах задания функции. В данной теме начинается работа по формированию у учащихся умений находить по формуле значение функции по известному значению аргумента, выполнять ту же задачу по графику и решать по графику обратную задачу. Функциональные понятия получают свою конкретизацию при изучении линейной функции и ее частного вида — прямой пропорциональности. Умения строить и читать графики этих функций широко используются как в самом курсе алгебры, так и в курсах геометрии и физики. Учащиеся должны понимать, как влияет знак коэффициента на расположение в координатной плоскости графика функции у = kх, где и k ≠ 0, как зависит от значений k и b взаимное расположение графиков двух функций вида у = kх + b.Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождаются рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры. |
| Глава 3. Степень с натуральным показателем | Степень с натуральным показателем и ее свойства. Одночлен. Функции у = х2, у = х3 и их графики. Основная цель — выработать умение выполнять действия над степенями с натуральными показателями. В данной теме дается определение степени с натуральным показателем. В курсе математики б класса учащиеся уже встречались с примерами возведения чисел в степень. В связи с вычислением значений степени в 7 классе дается представление нахождении значений степени с помощью калькулятора. Рассматриваются свойства степени с натуральным показателем. На примере доказательства свойств степени учащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материале. Свойства степени с натуральным показателем находят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений, содержащих степени, особое внимание следует обратить на порядок действий. Рассмотрение функций у = х2, у = х3 позволяет продолжить работу по формированию умений строить и читать графики функций. Важно обратить внимание учащихся на особенности графика функции у = х2: график проходит через начало координат, ось Оу является его осью симметрии, график расположен в верхней полуплоскости.Умение строить графики функций у = х2 и у = х3 используется для ознакомления учащихся с графическим способом решения уравнений. |
| Глава 4. Многочлены | Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители. Основная цель — выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Формируемые здесь формально-оперативные умения являются опорными при изучении действий с рациональными дробями, корнями, степенями с рациональными показателями. Изучение темы начинается с введения понятий многочлена, стандартного вида многочлена, степени многочлена. Основное место в этой теме занимают алгоритмы действий с многочленами — сложение, вычитание и умножение. Учащиеся должны понимать, что сумму, разность, произведение многочленов всегда можно представить в виде многочлена. Действия сложения, вычитания и умножения многочленов выступают как составной компонент в заданиях на преобразования целых выражений. Поэтому нецелесообразно переходить к комбинированным заданиям прежде, чем усвоены основные алгоритмы.Серьезное внимание в этой теме уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Соответствующие преобразования находят широкое применение как в курсе 7 класса, так и в последующих курсах, особенно в действиях с рациональными дробями.В данной теме учащиеся встречаются с примерами использования рассматриваемых преобразований при решении разнообразных задач, в частности при решении уравнений. Это позволяет в ходе изучения темы продолжить работу по формированию умения решать уравнения, а также решать задачи методом составления уравнений. В число упражнений включаются несложные задания на доказательство тождества. |
| Глава 5. Формулы сокращенного умножения | Формулы (а + b)2 = а2 ± 2аb + b2, (а ± b)3 = а3 ± За2b + Заb2 ± b3, (а ± b) (а2 + аb + b2) = а3 ±b3. Применение формул сокращенного умножения в преобразованиях выражений. Основная цель — выработать умение применять формулы сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители. В данной теме продолжается работа по формированию у учащихся умения выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам (а - b) (а + b) = а2 - b2, (а ± b)2 = а2 ± 2аb + b2. Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево». Наряду с указанными рассматриваются также формулы (а ± b)3 = а3± За2b + Заb2 ± b3, а3 ± b3 = (а ± b) (а2 + аb + b2). Однако они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использование. В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широкого круга задач. |
| Глава 6. Системы линейных уравнений | Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений. Основная цель — ознакомить учащихся со способом решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении текстовых задач.Изучение систем уравнений распределяется между курсами 7 и 9 классов. В 7 классе вводится понятие системы и рассматриваются системы линейных уравнений. Изложение начинается с введения понятия «линейное уравнение с двумя переменными». В систему упражнений включаются несложные задания на решение линейных уравнений с двумя переменными в целых числах.Формируется умение строить график уравнения а + bу = с, где а ≠ 0 или b ≠ 0, при различных значениях а, b, с. Введение графических образов дает возможность наглядно исследовать вопрос о числе решений системы двух линейных уравнений с двумя переменными. Основное место в данной теме занимает изучение алгоритмов решения систем двух линейных уравнений с двумя переменными способом подстановки и способом сложения. Введение систем позволяет значительно расширить круг текстовых задач, решаемых с помощью аппарата алгебры. Применение систем упрощает процесс перевода данных задачи с обычного языка на язык уравнений. |
| Общее кол-во часов | 101 |
Раздел III. Тематический план
| № п/п | Перечень разделов и последовательность их изучения | Кол-во часов на изучение каждого раздела | Сроки изучения разделов | Сроки контроля |
|
| Выражения, тождества, уравнения | 22 | 02.09 – 21.10 | 26.09 18.10 |
|
| Функции | 11 | 24.10 – 25.11 | 22.11 |
|
| Степень с натуральным показателем | 11 | 28.11 – 20.12 | 20.12 |
|
| Многочлены | 17 | 23.12 – 07.02 | 17.01 6.02 |
|
| Формулы сокращенного умножения | 19 | 10.02 – 3.04 | 16.03, 2.04 |
|
| Системы линейных уравнений | 16 | 6.04 – 18.05 | 15.05 |
|
| Повторение | 5 | 21.05 – 29.05 | |
| Итого | | 101 | | |
Согласовано:
Заместитель директора по УВР
________________ Липуга Е.Г.
РАЗДЕЛ 4. КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ.
| № урока | Тема урока
| Кол-во часов | Дата | Домашнее задание | ||||||||
| План | Факт | |||||||||||
| Выражения, тождества, уравнения (23) | ||||||||||||
| | 1 | Числовые выражения. | 1 | 02.09 |
| №6(ж,з,и) | ||||||
| | 2 | Выражения с переменной. | 1 | 05.09 |
| №7(а), №6(е) | ||||||
| | 3 | Сравнение значений выражений. | 1 | 06.09 |
| №51 | ||||||
| | 4 | Строгие и нестрогие неравенства. | 1 | 09.09 |
| №48(а,в,г) | ||||||
| | 5 | Свойства действий над числами. Примеры. | 1 | 12.09 |
| №54 | ||||||
| | 6 | Свойства действий над числами. Решение упражнений. | 1 | 13.09 |
|
| ||||||
| | 7 | Применение свойств действий над числами | 1 | 16.09 |
|
| ||||||
| | 8 | Тождества. Тождественные преобразования выражений. | 1 | 19.09 |
| №91 №95(в) | ||||||
| | 9 | Приведение подобных слагаемых. | 1 | 20.09 |
| №101(в), №102(б) | ||||||
| | 10 | Упрощение выражений. Раскрытие скобок. | 1 | 23.09 |
| №102(в,г) | ||||||
| | 11 | Входная контрольная работа №1. | 1 | 26.09 |
|
| ||||||
| | 12 | Анализ контрольной работы №1. | 1 | 27.09 |
|
| ||||||
| | 13 | Уравнение и его корни. | 1 | 30.09 |
| №127(в,г) | ||||||
| | 14 | Решение линейных уравнений. | 1 | 03.10 |
| №120(ж,з,и) | ||||||
| | 15 | Решение уравнений. Различные виды. Самостоятельная работа. | 1
| 04.10 |
| №130(д,е,ж) | ||||||
| | 16 | Решение простейших задач с помощью уравнений. | 1 | 07.10 |
| №144 | ||||||
| | 17 | Решение задач повышенной сложности с помощью уравнений. | 1 | 10.10 |
| №145 №132(в) | ||||||
| | 18 | Среднее арифметическое, размах, мода. Медиана как статистическая характеристика. | 1
| 11.10 |
| №133 | ||||||
| | 19 | Решение задач по теме «Статистические характеристики».Формулы. | 1 | 14.10 |
| №167
| ||||||
| | 20 | Обобщение изученного по теме «Уравнение и его корни». | 1 | 17.10 |
| №129, 133 | ||||||
| | 21 | Контрольная работа №2 по теме «Уравнение и его корни». | 1 | 18.10 |
|
| ||||||
| | 22 | Анализ контрольной работы | 1 | 21.10 |
|
| ||||||
| | Функция (11) | |||||||||||
| | | Что такое функция. Вычисление значений функции по формуле. | 1
| 24.10 |
| № 264, 262 | ||||||
| | | Различные способы задания функции. | 1 | 25.10 |
| №273№ 274 | ||||||
| | | График функции. Чтение графиков функции. | 1 | 07.11 |
| №277(б), 278(б) | ||||||
| | | Прямая пропорциональность и ее график. | 1 | 08.11 |
| №300(а,б) | ||||||
| | | Решение задач по теме «Прямая пропорциональность и ее график». | 1 | 11.11 |
| №301 | ||||||
| | | Решение задач по теме «Функция». | 1 | 14.11 |
| №304, №305(в) | ||||||
| | | Линейная функция и ее график. Угловой коэффициент прямой. | 1
| 15.11 |
| №319(ж,з,и) | ||||||
| | | Взаимное расположение графиков линейных функций. | 1 | 18.11 |
| №318(б), 319(ж,з) | ||||||
| | | Координаты точек пересечения графиков с осями координат. | 1 | 21.11 |
| №326, №327 | ||||||
| | | Контрольная работа №3 по теме «Функция». | 1 | 22.11
|
|
| ||||||
| | | Анализ контрольной работы | 1 | 25.11 |
|
| ||||||
| | Степень с натуральным показателем(11) | |||||||||||
| | | Степень. Определение. Свойства степени. | 1 | 28.11 |
| №375(в,г) №376(и) | ||||||
| | | Степень степени. Решение упражнений на применение свойств степени. | 1 | 29.11
|
| №377(д,е) №384(а,б) | ||||||
| | | Умножение и деление степеней. Свойства. Примеры. | 1 | 02.12 |
| №408(в,г) №415(в,е) | ||||||
| | | Решение упражнений по теме «Умножение и деление степеней». | 1 | 05.12 |
| №414(в,г,д) №415(в,г) | ||||||
| | | Возведение в степень произведения и степени. Правила. Примеры. | 1 | 06.12 |
| №429(а,б) №430(в,г,д) | ||||||
| | | Применение правил возведения в степень произведения и степени. | 1
| 09.12 |
| №433 №436(в,г) | ||||||
| | | Одночлен и его стандартный вид. | 1 | 12.12 |
| №457(д,г) №458(д) | ||||||
| | | Умножение одночленов. | 1 | 13.12 |
| №469(г,д,е) | ||||||
| | | Возведение одночлена в натуральную степень. | 1 | 16.12 |
| №473(в,г) №474(а) | ||||||
| | | Функции у=х | 1 | 19.12 |
| №487(в,г) | ||||||
| | | Контрольная работа №4 по теме «Степень с натуральным показателем». | 1 | 20.12 |
|
| ||||||
| | Многочлены(17) | |||||||||||
| | | Многочлен и его стандартный вид. | 1 | 23.12 |
| №589(в,г) №596(а) | ||||||
| | | Деление с остатком. | 1 | 26.12 |
| №570(в,г) №572(б) | ||||||
| | | Сложение и вычитание многочленов. Правило. Примеры. | 1 | 27.12 |
| №590(в,г) №605(г,д) | ||||||
| | | Сложение и вычитание многочленов. Решение упражнений. | 1 | 09.01 |
| №595(б,г) №595(б,г) | ||||||
| | | Умножение одночлена на многочлен. Правило. Примеры. | 1 | 10.01 |
| №615(г,дд) №№616(а) | ||||||
| | | Умножение одночлена на многочлен. Решение упражнений. | 1 | 13.01 |
| №№617(г,д,е) | ||||||
| | | Вынесение за скобку общего множителя. | 1 | 16.01 |
| №657(д,е,ж) №658(а) | ||||||
| | | Контрольная работа №5 по теме «Многочлены». | 1 | 17.01 |
|
| ||||||
| | | Анализ контрольной работы. | 1 | 20.01 |
| №638 | ||||||
| | | Умножение многочлена на многочлен. Решение упражнений. | 1 | 23.01 |
| №678(д,е) №679(д) | ||||||
| | | Умножение многочлена на многочлен. Самостоятельная работа. | 1 | 24.01 |
| №682(в,г) №683(д) | ||||||
| | | Умножение многочлена на многочлен. Обобщение по теме. | 1 | 27.01 |
| №684(в,г) №697(в) | ||||||
| | | Разложение многочлена на множители способом группировки. Примеры. | 1 | 30.01 |
| №698(б) №709(в) | ||||||
| | | Разложение многочлена на множители способом группировки. Решение упражнений. | 1 | 31.01
|
| №710 | ||||||
| | | Разложение многочлена на множители способом группировки. Самостоятельная работа. | 1 | 03.02 |
| №714(а) №716(а) | ||||||
| | | Контрольная работа №6 по теме «Многочлены». | 1 | 06.02 |
|
| ||||||
| | | Анализ контрольной работы | 1 | 07.02 |
|
| ||||||
| | Формулы сокращенного умножения(19) | |||||||||||
| | | Возведение в квадрат суммы и разности двух выражений. Формулы. Примеры. | 1 | 10.02
|
| №712(в,г) | ||||||
| | | Применение формул возведения в квадрат суммы и разности двух выражений. | 1 | 13.02 |
| №808)а,б) №812(а.б) | ||||||
| | | Самостоятельная работа на применение формул возведения в квадрат суммы и разности двух выражений. | 1 | 14.02
|
| №804 | ||||||
| | | Возведение в куб суммы и разности двух выражений. Возведение двучлена в степень. | 1 | 17.02 |
| №834(г,д,е) №835(в) | ||||||
| | | Разложение на множители с помощью квадрата суммы и квадрата разности. Примеры. | 1 | 20.02 |
| №840(б) №844(а,б) | ||||||
| | | Разложение на множители с помощью квадрата суммы и квадрата разности. Решение упражнений. | 1 | 21.02
|
| №855(а,б,в) №854(ж) | ||||||
| | | Умножение разности двух выражений на их сумму. Примеры. | 1 | 27.02 |
| №867(а,б,в) №873(г) | ||||||
| | | Умножение разности двух выражений на их сумму. Решение упражнений. | 1 | 28.02 |
| №889(а,б) №893(г,д) | ||||||
| | | Умножение разности двух выражений на их сумму. Самостоятельная работа. | 1 | 02.03 |
| №884(3 стол) №885(г) | ||||||
| | | Разложение разности квадратов на множители. Примеры. | 1 | 05.03 |
| №808(а,б) №884(2 стол) | ||||||
| | | Разложение разности квадратов на множители. Решение упражнений. | 1 | 6.03
|
| №893(а,б,в) №895(а,б) | ||||||
| | | Разложение разности квадратов на множители. Самостоятельная работа. | 1 | 12.03 |
|
| ||||||
| | | Разложение на множители суммы и разности кубов. | 1 | 13.03 |
|
| ||||||
| | | Контрольная работа №7 по теме «Формулы сокращенного умножения». | 1 | 16.03 |
|
| ||||||
| | | Преобразование целого выражения в многочлен. Примеры. | 1 | 19.03 |
| №885(ж,з,и) №835(д,е) | ||||||
| | | Преобразование целого выражения в многочлен. Решение упражнений. | 1 | 20.03 |
| №920(в,г) №921(б) | ||||||
| | | Применение различных способов для разложения на множители. Примеры. | 1 | 30.03
|
| №935(в,г) №936(а,б) | ||||||
| | | Контрольная работа №8 по теме «Формулы сокращенного умножения». | 1 | 2.04 |
| №939(г,д,е) №941(а) | ||||||
| | | Анализ контрольной работы. | 1 | 3.04 |
|
| ||||||
| | Системы линейных уравнений(16) | |||||||||||
| | | Линейные уравнения с двумя переменными и его решение. Определения. Примеры. | 1 | 06.04 |
| №1028 №1029(б) | ||||||
| | | Свойства линейных уравнений с двумя переменными. | 1 | 9.04
|
| №1048(в,г) №1049(а) | ||||||
| | | График линейного уравнения с двумя переменными. Определение, примеры. | 1 | 10.04 |
| №1050(а,б) №1052 | ||||||
| | | Построение графика линейного уравнения с двумя переменными. | 1 | 13.04 |
| №1058(б) №1060(б) | ||||||
| | | Системы линейных уравнений с двумя переменными. Определение. Примеры. | 1 | 16.04
|
| №1061(б) №1062(в) | ||||||
| | | Системы линейных уравнений с двумя переменными. Решение упражнений. | 1 | 17.04 |
| №1062(е) №1063(а) | ||||||
| | | Системы линейных уравнений с двумя переменными. Самостоятельная работа. | 1 | 20.04
|
| №1069(в,г) | ||||||
| | | Способ подстановки. Алгоритм. Примеры. | 1 | 23.04 |
| №1070(в,г) | ||||||
| | | Применение способа подстановки. | 1 | 24.04 |
| №1071(в) № 1072(в,г) | ||||||
| | | Способ сложения. Алгоритм. Примеры. | 1 | 27.04 |
| №1083(а,б) №1084(б) | ||||||
| | | Применение способа сложения. | 1 | 30.04 |
| №1085(а,б) №1084(г) | ||||||
| | | Решение задач по теме «Системы линейных уравнений». Линейные неравенства с двумя переменными и их системы. | 1 | 7.05 |
| №1086(а) №1095(в,г) | ||||||
| | | Решение простейших задач с помощью систем уравнений. | 1 | 8.05 |
| №1100 | ||||||
| | | Решение задач повышенной сложности с помощью систем уравнений. | 1 | 14.05 |
| №1102 | ||||||
| | | Итоговая контрольная работа. | 1 | 15.05
|
|
| ||||||
| | | Анализ контрольной работы. |
| 18.05 |
|
| ||||||
| | Повторение(5) | |||||||||||
| | | Повторение. Выражения, тождества, уравнения. Одночлены. Многочлены. Формулы сокращенного умножения | 1 | 21.05 |
| №1115 | ||||||
| | | Повторение. | 1 | 22.05
|
|
| ||||||
| | | Повторение. | 1 | 25.05 |
|
| ||||||
| | | Повторение. | 1 | 28.05 |
|
| ||||||
| | | Повторение. | 1 | 29.05 |
|
| ||||||
Контрольная работа №1 по теме «Преобразование выражений»
Вариант 1
• 1. Найдите значение выражения 6x - 8y, при x = 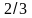 , у =
, у = 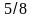 .
.
• 2. Сравните значения выражений -0,8x - 1 и 0,8x - 1 при x= 6.
• 3. Упростите выражение:
а) 2x - Зy- 11х + 8у;б) 5(2а + 1) - 3;в) 14x - (x - 1) + (2х + 6).
4. Упростите выражение и найдите его значение:
-4 (2,5а - 1,5) + 5,5а– 8, при а = -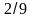 .
.
5. Из двух городов, расстояние между которыми sкм, одновременно навстречу друг другу выехали легковой автомобиль и грузовик и встретились через tч. Скорость легкового автомобиля v км/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, еcли s = 200, t= 2, v= 60.
6. Раскройте скобки: Зx- (5x - (3x- 1)).
Контрольная работа №1 по теме «Преобразование выражений»
Вариант 2
•1. Найдите значение выражения 16а + 2y,приа = 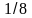 , у = -
, у = - 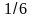 .
.
•2. Сравните значения выражений 2 + 0,3а и 2 - 0,3а,при а = - 9.
•3. Упростите выражение:
а) 5а + 7b - 2а - 8b;б)3 (4x + 2) - 5;в)20b - (b- 3) + (Зb - 10).
4.Упростите выражение и найдите его значение:
-6 (0,5x - 1,5) - 4,5x– 8, при x = 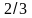 .
.
5. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл и встретились через tч. Найдите расстояние между городами, если скорость автомобиля v1км/ч, а скорость мотоцикла v2км/ч. Ответьте на вопрос задачи, если:t = 3, v1= 80, v2 = 60.
6. Раскройте скобки: 2р - (3р - (2р - с)).
Контрольная работа №2 «Уравнения с одной переменной»
Вариант 1
•1. Решите уравнение:
| а) б) 6x - 10,2 = 0; | в) 5x - 4,5 = 3x + 2,5; г) 2x - (6x - 5) = 45. |
• 2. Таня в школу сначала едет на автобусе, а потом идет пешком. Вся дорога у нее занимает 26 мин. Идет она на 6 мин дольше, чем едет на автобусе. Сколько минут она едет на автобусе?
3. В двух сараях сложено сено, причем в первом сарае сена в 3 раза больше, чем во втором. После того как из первого сарая увезли 20 т сена, а во второй привезли 10 т, в обоих сараях сена стало поровну. Сколько всего тонн сена было в двух сараях первоначально?
4. Решите уравнение 7х - (х+ 3) = 3 (2х - 1).
Контрольная работа №2 «Уравнения с одной переменной»
Вариант 2
• 1. Решите уравнение:
| а) б) 7x + 11,9 = 0; | в) 6х - 0,8 = 3х + 2,2; г) 5х - (7х + 7) = 9. |
•2. Часть пути в 600 км турист пролетел на самолете, а часть проехал на автобусе. На самолете он проделал путь, в 9 раз больший, чемна автобусе. Сколько километров турист проехал на автобусе?
3. На одном участке было в 5 раз больше саженцев смородины, чем на другом. После того как с первого участка увезли 50 саженцев, а на второй посадили еще 90, на обоих участках саженцев стало поровну. Сколько всего саженцев было на двух участках первоначально?
4. Решите уравнение 6х - (2х - 5) = 2 (2х + 4)
Контрольная работа №3 по теме «Линейная функция»
Вариант 1
•1. Функция задана формулой у = 6х + 19. Определите: а) значение у, если х = 0,5; б) значение х, при котором у = 1; в) проходит ли график функции через точкуА(-2; 7).
•2. а) Постройте график функции у = 2х - 4.
б) Укажите с помощью графика, чему равно значение упри х = 1,5.
•3. В одной и той же системе координат постройте графики функций: а) у = -2х; б) у = 3.
4. Найдите координаты точки пересечения графиков функций у = 47х - 37 и у = -13х + 23.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = 3х - 7 и проходит через начало координат.
Контрольная работа №3 по теме «Линейная функция»
Вариант 2
•1. Функция задана формулой у = 4х - 30. Определите:
а)значение у, если х = -2,5; б) значение х, при которому = -6; в) проходит ли график функции через точкуВ(7; -3).
•2. а) Постройте график функции у = -3х + 3.
б) Укажите с помощью графика, при каком значении х значение уравно 6.
•3. В одной и той же системе координат постройте графики функций: а) у = 0,5х; б) у = -4.
4. Найдите координаты точки пересечения графиков функций у = -38х + 15 и у = -21х - 36.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = -5х + 8 и проходит через начало координат.
Контрольная работа №4
по теме «Степень с натуральным показателем»
Вариант 1
• 1. Найдите значение выражения 1 - 5х2, при х = -4.
• 2. Выполните действия:
а) y7•y12;б) y20:y5;в) (y2)8; г) (2у)4.
• 3. Упростите выражение: а) -2аb3•3а2 • b4;б) (-2а5b2)3.
•4. Постройте график функции у = х2. С помощью графика определите значение уприх=1,5; х = -1,5.
5. Вычислите: 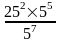 .
.
6. Упростите выражение:a) 2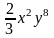 •
•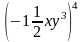 ; б) xn– 2 •x3 – n•x.
; б) xn– 2 •x3 – n•x.
Контрольная работа №4
по теме «Степень с натуральным показателем»
Вариант 2
• 1. Найдите значение выражения -9р3,при р= - 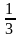 .
.
• 2. Выполните действия: а) с3• с22;б) с18:с6; в) (с4)6; г) (3с)5.
• 3. Упростите выражение: а) -4х5у2•Зху4; б) (Зх2y3)2.
•4. Постройте график функции у = х2. С помощью графика функции определите, при каких значениях х значение yравно 4.
5. Вычислите: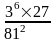 .
.
6. Упростите выражение:a) 3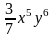 •
•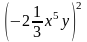 ; б)(an+1)2:a2n.
; б)(an+1)2:a2n.
Контрольная работа №5 по теме «Сумма, разность многочленов»
Вариант 1
•1. Выполните действия: а)(За - 4ах + 2) - (11а - 14ах); б)3у2 (у3 + 1).
•2.Вынесите общий множитель за скобки: а)10аb- 15b2; б) 18а3 + 6а2.
•3.Решите уравнение 9х - 6 (х - 1) = 5 (х + 2).
•4. Пассажирский поезд за 4 ч прошел такое же расстояние, какое товарный за 6 ч. Найдите скорость пассажирского поезда ,если известно, что скорость товарного на 20 км/ч меньше.
5.Решите уравнение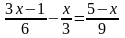 .
.
6.Упростите выражение2а (а + b- с) –2b(а - b - с) + 2с (а - b + с).
Контрольная работа №5 по теме «Сумма, разность многочленов»
Вариант 2
•1. Выполните действия: а)(2а2 - За + 1) - (7а2 - 5а); б) 3х(4х2- х).
•2.Вынесите общий множитель за скобки: а)2ху - 3ху2; б) 8b4 + 2b3.
•3.Решите уравнение 7-4 (3х - 1) = 5 (1 - 2х).
•4. В трех шестых классах 91 ученик. В 6 «А» на 2 ученика меньше, чем в 6 «Б», а в 6 «В» на 3 ученика больше, чем в 6 «Б». Сколько учащихся в каждом классе?
5.Решите уравнение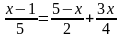 .
.
6.Упростите выражение 3х(х + у + с) - 3у (х - у - с) - 3с(х + у - с).
Контрольная работа №6 по теме «Произведение многочленов»
Вариант 1
•1. Выполните умножение:
а) (с + 2) (с - 3); б) (2а - 1) (За + 4); в) (5х - 2у) (4х - у);г) (а - 2) (а2 - 3а + 6).
•2. Разложите на множители: а) а (а + 3) - 2 (а + 3); б) ах-ау + 5х - 5у.
3. Упростите выражение -0,1x (2х2 + 6) (5 - 4х2).
4. Представьте многочлен в виде произведения:
а) х2 - ху- 4х + 4у;б) ab - ас - bх + сх + с - 6.
5. Из прямоугольного листа фанеры вырезали квадратную пластинку, для чего с одной стороны листа фанеры отрезали полосу шириной 2 см, а с другой, соседней, -3 см. Найдите сторону получившегося квадрата, если известно, что его площадь на51 см2 меньше площади прямоугольника.
Контрольная работа №6 по теме «Произведение многочленов»
Вариант 2
•1. Выполните умножение: а)(а-5)(а-3);б)(5х + 4) (2х - 1);
в) (3р + 2с) (2р + 4с); г) (6 - 2) (b2+ 2b - 3).
•2. Разложите на множители: а) х (х - у) + а (х - у);б) 2а- 2b + са - сb.
3. Упростите выражение 0,5х (4х2 - 1) (5х2 + 2).
4. Представьте многочлен в виде произведения:
а) 2а - ас - 2с + с2;6) bx + by - х - у - ах - ау.
5. Бассейн имеет прямоугольную форму. Одна из его сторона 6 м больше другой. Он окружен дорожкой, ширина которой0,5 м. Найдите стороны бассейна, если площадь окружающей его дорожки 15 м2.
Контрольная работа №7
по теме «Формулы сокращенного умножения»
Вариант 1
•1. Преобразуйте в многочлен:
а)(у -2)2; б)(6х + а)2; в) (6с - 1) (6с + 1);г) (2а + 4b) (2а- 4b).
•2. Упростите выражение (а - 8)2 - (64 + 2а).
•3. Разложите на множители: а) х2 - 81; б) 16х2 - 8ху + у2.
4. Решите уравнение (2 - х)2 - х (х + 1,5) = 4.
5. Выполните действия: а) (у2 - 3а) (3а + у2); б) (4х2 + х)2; в) (3 + т)2 (3 - т)2.
6.Разложите на множители: а) 4х2y2-9а4; б) 25а2 - (а + 3)2; в) 27т3 + п3.
Контрольная работа №7
по теме «Формулы сокращенного умножения»
Вариант 2
•1. Преобразуйте в многочлен:
а)(3а + 5)2;б)(3х -b)2;в) (2b + 3) (2b - 3);г)(5у - х) (5у + х).
•2. Упростите выражение (с + b) (с - b) - (5с2 - b2).
•3. Разложите на множители: а) 36у2 - а2;б) с2 + 4bс + 4b2.
4. Решите уравнение 12 - (4 - х)2 = х (3 - х).
5. Выполните действия: а) (3х + у2) (3х - у2); б) (а3 - 6а)2; в) (а - х)2 (х + а)2.
6.Разложите на множители: а) 100а4 -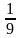 b2 ; б) 9х2 - (х - 1)2; в) х3 + у6.
b2 ; б) 9х2 - (х - 1)2; в) х3 + у6.
По учебнику « Алгебра 7 класс» Авторы: под редакцией Ю.Н. Макарычева, Н.Г. Миндюк,
Контрольная работа №8
по теме «Преобразование целых выражений»
Вариант 1
• 1. Упростите выражение:
а) (х - 3) (х - 7) - 2х (3х - 5); б) 4а (а - 2) - (а - 4)2;в)2 (т + 1)2 - 4m.
• 2. Разложите на множители: а) х3 - 9х; б) -5а2 - 10аb - 5b2.
3. Упростите выражение(у2 - 2у)2 -у2(у + 3) (у - 3) + 2у (2у2 + 5).
4. Разложите на множители: а) 16х4 - 81; б) х2 - х - у2 - у.
5. Докажите, что выражение х2 - 4х + 9, при любых значениях х принимает положительные значения.
Контрольная работа №8
по теме «Преобразование целых выражений»
Вариант 2
•1. Упростите выражение:
а) 2х (х - 3) - 3х (х + 5); б) (а + 7) (а - 1) + (а - 3)2; в) 3 (у + 5)2 - 3у2.
•2. Разложите на множители: а) с2 - 16с; б) 3а2 - 6аb + 3b2.
3. Упростите выражение(За - а2)2 -а2(а- 2)(а + 2) + 2а (7 + 3а2).
4. Разложите на множители: а) 81а4 - 1; б) у2 - х2 - 6х - 9.
5. Докажите, что выражение -а2 + 4а - 9 может принимать лишь отрицательные значения.
Контрольная работа №9 по теме «Системы линейных уравнений»
Вариант 1
• 1. Решите систему уравнений
4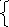 х+у = 3,
х+у = 3,
6х-2у = 1.
•2. Банк продал предпринимателю г-ну Разину 8 облигаций по 2000 р. и 3000 р. Сколько облигаций каждого номинала купил г-н Разин, если за все облигации было заплачено 19000 р.?
| 3. Решите систему уравнений 2 2х + 10= 3 - (6х + 5у). | 4. Прямая у = кх + b проходит через точкиА (3; 8) иВ(-4; 1). Напишите уравнение этой прямой. |
5. Выясните, имеет ли решение система
3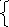 x - 2y = 7,
x - 2y = 7,
6х - 4y = 1.
Контрольная работа №9по теме «Системы линейных уравнений»
Вариант 2
•1. Решите систему уравнений
3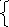 х-у = 7,
х-у = 7,
2х + 3у = 1.
• 2. Велосипедист ехал 2 ч по лесной дороге и 1 ч по шоссе, всего он проехал 40 км. Скорость его на шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист ехал по шоссе, и с какой по лесной дороге?
| 3. Решите систему уравнений 2 5 - (х - 2у) = 4у + 16. | 4. Прямая у = kx + bпроходит через точкиА (5; 0) иВ(-2; 21). Напишите уравнение этой прямой. |
5. Выясните, имеет ли решения система и сколько:
5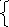 х-у =11,
х-у =11,
-10х + 2у = -22.
Итоговая контрольная работа по алгебре в 7 классе
Вариант 1
•1. Упростите выражение: а) 3а2b • (-5а3b); б) (2х2у)3.
•2. Решите уравнение 3х - 5 (2х + 1) = 3 (3 - 2х).
• 3. Разложите на множители: а) 2ху - 6y2; б) а3- 4а.
• 4. Периметр треугольника ABCравен 50 см. Сторона АВ на 2 см больше стороны ВС, а сторона АС в 2 раза больше стороны ВС. Найдите стороны треугольника.
5.Докажите, что верно равенство
(а + с) (а - с)- b(2а - b)- (а - b + с) (а -b- с) = 0.
6.На графике функции у = 5х - 8 найдите точку, абсцисс которой противоположна ее ординате.
Итоговая контрольная работа по алгебре в 7 классе
Вариант 2
•1. Упростите выражение: а) -2ху2 • Зх3у5; б) (-4аb3)2.
•2. Решите уравнение4 (1 - 5х) = 9 - 3 (6x - 5).
•3. Разложите на множители: а) а2b - аb2; б) 9х - х3.
•4. Турист прошел 50 км за 3 дня. Во второй день он прошел на 10 км меньше, чем в первый день, и на 5 км больше, чем в третий. Сколько километров проходил турист каждый день?
5.Докажите, что при любых значениях переменных верно равенство
(х - у) (х + у) - (а - х + у) (а - х - у) - а (2х-а) = 0.
6.На графике функции у = 3х + 8 найдите точку, абсцисса которой равна ее ординате.
Критерии оценок по математике
Рекомендации по оценке знаний и умений учащихся по математике
1. Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.
2. Основными формами проверки знаний и умений учащихся по математике являются письменная контрольная работа и устный опрос.
При оценке письменных и устных ответов учитель в первую очередь учитывает показанные учащимися знания и умения. Оценка зависит также от наличия и характера погрешностей, допущенных учащимися.
3. Среди погрешностей выделяются ошибки и недочеты. Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе.
К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в программе основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения; неаккуратная запись; небрежное выполнение чертежа.
Граница между ошибками и недочетами является в некоторой степени условной. При одних обстоятельствах допущенная учащимися погрешность может рассматриваться учителем как ошибка, в другое время и при других обстоятельствах — как недочет.
4. Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.
Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты я обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью.
Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
5. Оценка ответа учащегося при устном и письменном опросе проводится по пятибалльной системе, т. е. за ответ выставляется одна из отметок: 2 (неудовлетворительно), 3 (удовлетворительно), 4 (хорошо), 5 (отлично).
6
Критерии ошибок
К г р у б ы м ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять; незнание приемов решения задач, рассматриваемых в учебниках, а также вычислительные ошибки, если они не являются опиской;
К н е г р у б ы м ошибкам относятся: потеря корня или сохранение в ответе постороннего корня; отбрасывание без объяснений одного из них и равнозначные им;
К н е д о ч е т а м относятся: нерациональное решение, описки, недостаточность или отсутствие пояснений, обоснований в решениях
Оценка устных ответов учащихся
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником,
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при отработке умений и навыков;
отвечал самостоятельно без наводящих вопросов учителя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные по замечанию учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.
Отметка «3» ставится в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»);
имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная формулировка основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Оценка письменных работ учащихся
Отметка «5» ставится, если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что учащийся не владеет
обязательными умениями по данной теме в полной мере.
Критерии оценок за письменную экзаменационную работу по математике
Оценка «5» ставится, если ученик:
Выполнил работу без ошибок и недочетов.
Допустил не более одного недочета
Оценка «4» ставится, если ученик выполнил работу полностью, но допустил в ней:
Не более одной негрубой ошибки и одного недочета.
Не более двух недочетов.
Оценка «3» ставится, если ученик правильно выполнил не менее половины работы или допустил:
Не более двух грубых ошибок или не более одной грубой и одной негрубой ошибки и одного недочета;
Не более двух- трех негрубых ошибок или одной негрубой ошибки и трех недочетов;
При отсутствии ошибок, но при наличии четырех-пяти недочетов.
Оценка «2» ставится, если ученик:
Допустил число ошибок недочетов превышающее норму, при которой может быть выставлена оценка «3».
Если правильно выполнил менее половины работы.
Не приступил к выполнению работы.
Правильно выполнил не более 10% всех заданий.
Пояснительная записка
Рабочая программа по математике (алгебре) для 7 класса составлена на основе авторской программы «Программа общеобразовательных учреждений по алгебре 7–9 классы» (авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова, составитель Т.А. Бурмистрова. – М.: «Просвещение», 2014).
Рабочая программа рассчитана на 117 час в год: 5 часов в неделю (понедельник -8, вторник -8, среда- 8, четверг-8, пятница -9, всего-41 час) в 1 четверти и 3 часа в неделю (вторник – 26, четверг – 26, пятница – 24, всего -76 часов) в 2-4 четвертях.
Настоящая рабочая программа по математикедля 7 класса составлена на основе Фундаментального ядра содержания общего образования и Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования, с учетом преемственности на основании следующих нормативных правовых документов:
Закона РФ от 10 июля 1992 года №3266-1 (ред. от 27.12.2009г.) «Об образовании»;
Федерального компонента государственного стандарта среднего (полного) общего образования, утвержденного приказом Министерства образования РФ от 05.03.2004 №1089;
Приказа Министерства образования РФ «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2017/2018 учебный год»;
Приказ МОиН РФ №1897 от 17.12.2010г. «Об утверждении ФГОС ООО» п.18.2.2;
Положения МБОУ СОШ №16 х. Арбузова о структуре, порядке разработки, рассмотрения и утверждения рабочих учебных программ, реализуемых школой (принято на заседании педагогического совета МБОУ СОШ №16 х. Арбузова, протокол;
Сборник рабочих программ. 7-9 классы: пособие для учителей общеобразоват. учреждений / сост. Т.А.Бурмистрова. – М.: Просвещение, 2014), федерального перечня учебников, рекомендованных или допущенных к использованию в образовательном процессе в образовательных учреждениях, базисного учебного плана, тематического планирования учебного материала, с учетом преемственности.
В ней также учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий (УУД) для основного общего образования.
Цели курса:
В направлении личностного развития:
1) развитие логического и практического мышления, культуры речи, способности к умственному эксперименту;
2) формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
3) воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
4) формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
5) развитие интереса к математическому творчеству и математических способностей.
В метапредметном направлении:
1) формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
2) развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
3) формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимых для различных сфер человеческой деятельности.
В предметном направлении:
1) овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучение смежных дисциплин, применения в повседневной жизни;
2) создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Используется учебно-методический комплект:
Для учителя:
1. Рурукин А.Н., Лупенко Г.В., Масленникова И.А. Поурочные разработки по алгебре к учебнику Ю.Н.Макарычева, Москва, ВАКО, 2014
2. Макарычев, Ю. Н. Алгебра: учебник для 7 класса общеобразовательных учреждений / Ю. Н. Макарычев, К. И. Нешков, Н. Г. Миндюк, С. Б. Суворова; под ред. С. А. Теляковского. - М.: Просвещение, 2014.
3. Звавич, Л. И. Дидактические материалы по алгебре. 7 класс / Л. И. Звавич, Л. В. Кузнецова, С. Б. Суворова. - М.: Просвещение, 2011.
Для учащихся
1. Учебник: Алгебра 7 класс: для общеобразовательных учреждений/Ю.Н.Макарычев, Н.Г.миндюк и др.; под ред. С.А. Теляковского, изд.М.: Просвещение,2014г.
2.Тесты по алгебре. 7 класс:7 класс /Ю.А.Глазков, М.Я. Гаиашвили,- М,: изд. «Экзамен», 2010
3. Дидактические материалы по алгебре для 7 класса. Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова, изд. Москва «Просвещение» 2011
Интернет-ресурс
1. www. edu - "Российское образование"Федеральный портал.
2. www. school.edu - "Российский общеобразовательный портал".
3. www.school-collection.edu.ru/ Единая коллекция цифровых образовательных ресурсов
4. www.mathvaz.ru - docье школьного учителя математики

 Получите свидетельство
Получите свидетельство Вход
Вход


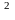 и у=х
и у=х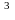 и их графики.
и их графики.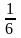 х = 18;
х = 18;








 Рабочая программа (138.62 KB)
Рабочая программа (138.62 KB)
 0
0 122
122 1
1 Нравится
0
Нравится
0




