ЦЕЛЬ УРОКА: ввести понятие прямоугольного параллелепипеда; сформировать навык решения задач по изученной теме.
ЗАДАЧИ УРОКА:
- рассмотреть свойства его граней, двугранных углов, сформулировать и доказать теорему о диагоналях прямоугольного параллелепипеда,
- способствовать развитию логического и образного мышления;
- воспитывать аккуратность при выполнении чертежей и рисунков.
ХОД УРОКА
- Организационный момент (формулировка темы и целей урока).
- Актуализация знаний, подготовка к восприятию новой темы.
(проверка у доски домашнего задания).
3. - Во время выполнения домашней задачи с остальными учащимися проводится устная работа.
Эта работа проходит следующим образом: Мы будем разгадывать кроссворд. Только кроссворд у нас не совсем обычный. Если вы обратили внимание, то некоторые слова уже в него вписаны. В этом случае мы будем выполнять задание «наоборот»- нужно дать определение вписанным словам.
Итак, приступим.
Кроссворд
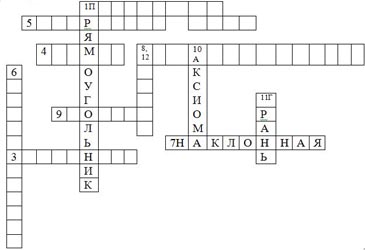
- Поверхность, имеющая два измерения. (ПЛОСКОСТЬ)
- !!! ПРЯМОУГОЛЬНИК. ОПР. Прямоугольником называется параллелограмм, у которого все углы прямые.
- Отрезок, соединяющий любые две вершины многогранника, не принадлежащие одной грани. (ДИАГОНАЛЬ)
-
Угол, градусная мера которого 900
- Фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не лежащими в одной плоскости. ( ДВУГРАННЫЙ УГОЛ)
- Как называется отрезок АВ на рисунке? (ПЕРПЕНДИКУЛЯР)
- !!! НАКЛОННАЯ. ОПР. Наклонная- отрезок, соединяющий точку А с точкой, лежащей в плоскости α, отличный от перпендикуляра.
- !!! ПРЯМАЯ. ОПР. Линия не имеющая ни начала, ни конца.
- Предложение, выражающее свойство геометрической фигуры, требующее доказательства. (ТЕОРЕМА)
- !!! АКСИОМА. ОПР. Утверждение, не требующее доказательства.
- !!! ГРАНЬ. ОПР. Многоугольники, из которых составлен многогранник, называют гранями.
- Многогранник, изображенный на рисунке? (ПАРАЛЛЕЛЕПИПЕД)
4 .Объяснение новой темы.
В ходе разгадывания кроссворда мы повторили основные понятия, теперь можем перейти к изучению новой темы.
- С понятием прямоугольного параллелепипеда вы впервые познакомились еще в пятом классе. Уже тогда вы узнали как выглядит прямоугольный параллелепипед, как правильно изобразить его на рисунке, что называется гранями, вершинами, ребрами прямоугольного параллелепипеда. С понятием параллелепипеда мы с вами знакомились уже в 10 классе. Перед вами модели фигур. Из представленных фигур выберите параллелепипеды, а из них, в свою очередь, прямоугольные параллелепипеды. ( Учащиеся выбирают. Рекомендуется вызвать слабого ученика .
А теперь давайте попробуем ответить на вопрос: чем вы руководствовались при выборе? Попробуйте дать определение прямоугольного параллелепипеда.
Определение. Параллелепипед называется прямоугольным, если его основания представляют собой прямоугольники, а боковые ребра перпендикулярны основаниям.
Сформулируем теперь свойства прямоугольного параллелепипеда.
Мы уже сказали, что основания- прямоугольники. А что можно сказать о боковых гранях? (ТОЖЕ ПРЯМОУГОЛЬНИКИ).
Таким образом, мы сформулировали первое свойство :
Все грани прямоугольного параллелепипеда- прямоугольники.
Для формулировки остальных свойств воспользуемся аналогией с прямоугольником.
|
Прямоугольник |
Прямоугольный параллелепипед |
|
Все углы прямые. |
Все двугранные углы- прямые. |
|
Диагонали прямоугольника равны. |
Диагонали прямоугольного параллелепипеда равны. |
Докажем последнее свойство, пользуясь готовым рисунком.
Рассмотрим диагональное сечение BB1DD1
Прежде чем перейти к следующему свойству, введем понятьия измерений прямоугольного параллелепипеда.
Длины трех ребер, имеющих общую вершину, называют измерениями прямоугольного параллелепипеда.
Обычно их называют длина, ширина, высота.
В прямоугольнике квадрат диагонали равен сумме квадратов его сторон. ( пользуясь теоремой Пифагора)
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. (пространственная теорема Пифагора)
Докажем это свойство.
Дано: ABCDA1B1C1D1- прямоугольный параллелепипед, AA1=а, АВ= в, АД= с.
Доказать, что AC1=a2+b2+c2
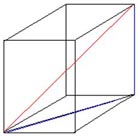
Доказательство - смотри документ.
5. Решение задач по учебнику
6. Домашнее задание (разноуровневое)
7. Подведение итогов.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Прямоугольный параллелепипед (0.11 MB)
Прямоугольный параллелепипед (0.11 MB)
 0
0 1123
1123 8
8 Нравится
0
Нравится
0


