Материал на украинском языке.
Мета:
- Систематизувати і узагальнити знання отримані на попередніх заняттях;
- учити вмінню докладно і переконливо робити доповідь на задану тему;
- розвивати інтерес до математики , показати практичне використання математичних понять в звичайних життєвих ситуаціях.
Вид заняття: рольова гра - судове слухання.
Обладнання: плакати з ілюстраціями до задач.
Хід засідання.
Вступ.( керівник гуртка)
Вивчення математики дає великі можливості не тільки в плані розвитку здібностей студентів, але здатне в деякій мірі сформувати інтерес до майбутньої професії. Якщо говорити про майбутніх бухгалтерів, фінансистів, програмістів, то можна з впевненістю твердити, що математика в їх житті посідає особливе місце – не тільки як предмет, а як інструмент професійної діяльності.
Традиційний курс математики в основному формалізований і має абстрактний характер, тому на засіданнях гуртка розглядались приклади практичного використання знань , отриманих на навчальних заняттях. Сьогодні члени гуртка продемонструють узагальнений досвід, отриманий на попередніх заняттях. Запрошуємо взяти участь у відкритому засіданні математичного гуртка, яке проводиться у вигляді судового слухання.
Основна частина.
Судовий розпорядник: Встати, суд іде.
Суддя . Сідайте. Починаємо слухання справи « Пряма і студенти».
Поступило кілька позовних заяв даної справи.
Пане розпоряднику, запросіть першого позивача .
Перший позивач. Я висуваю позов щодо того ,що пряма весь час змінює свій нахил. Я не можу збагнути, для чого це потрібно?
Суддя. Відповідач «Пряма», які роз’яснення ви можете надати?
Відповідач дає роз’яснення ( «Рівняння прямої», додаток 4.1)
Суддя до позивача: Тепер ви зрозуміли суть питання ?
Перший позивач: Ваша честь, я дуже старався, але не з’ясував необхідність поняття «кутовий коефіцієнт» і що таке ухил ? Суддя до прямої : Ваші роз’яснення не внесли повної ясності. Які ще аргументи ви можете надати?
Відповідач: Ваша честь, можна запросити свідка?
Суддя до розпорядника: Запросіть, будь ласка, свідка.
Перший свідок: Я можу навести переконливі аргументи на захист особливостей поведінки прямої ( додаток 4. 2) Давайте розглянемо «Задачу про ухил шляху»
Суддя: Позивач, чи є ще питання?
Перший позивач: Дякую за роз’яснення . Тепер я зрозумів важливість такої поведінки прямої і відхиляю свій позов.
Суддя до прямої: На жаль, ще є кілька позовних заяв. Розпоряднику, запросіть наступного позивача.
Другий позивач: Я бажаю отримати пояснення з приводу дивної поведінки графіка прямої: то він чомусь зростає, то чомусь починає спадати, а зовсім перестає змінюватись! Тож навіщо так заплутувати студентів?
Суддя : Суть позову зрозуміла . Відповідач, які роз’яснення ви можете навести?
Відповідач: Для подання роз’яснення я прошу запросити другого свідка.
Другий свідок: давайте розглянемо причину дивної поведінки графіка прямої на прикладі задачі про басейн ( додаток 4. 3)
Суддя: позивачу, чи зрозуміли ви необхідність такої поведінки графіка прямої?
Другий позивач: Ваша честь, у мене є невпевненість щодо такого пояснення .
Суддя : Відповідачу, що ще ви можете запропонувати на захист дивної поведінки графіка прямої?
Відповідач : Ваша честь,запросіть,будь ласка, наступного свідка.
Третій свідок: Коли ми мандруємо в потягах, то навряд чи ми замислюємося про безпеку на залізничному транспорті . Так ось, саме дивна поведінка графіка прямої допомагає диспетчерам забезпечувати безпеку на залізничному транспорті . Давайте розглянемо приклад задачі про графік руху.( додаток 4.4)
Другий позивач: Ваша честь , я відхиляю свій позов, тому що мені дуже докладно пояснили причини та необхідність різної поведінки графіка прямої.
Суддя : Пане розпоряднику, запросіть наступного позивача.
Третій позивач: Ваша честь, я - майбутній бухгалтер, не розумію корисності прямої для рішення економічних задач.
Суддя : Відповідач, що ви можете сказати з приводу економічної доцільності застосування прямої?
Відповідач : Пропоную вислухати аргументи наступних свідків.
Суддя: Пане розпоряднику, запросіть наступного свідка.
Четвертий свідок: В багатьох кафе у вечірній час, використовують свічки, не стільки для економії освітлення, а для створення більш романтичного спілкування. Власник кафе повинен правильно скласти бюджет закладу ,тому він повинен знати , з якою швидкістю горить свічка, який час і яку кількість свічок треба придбати (плакат № 5)
П’ятий свідок: Я - студентка 2-го курсу бухгалтерського обліку, можу роз’яснити першокурсницям , як важливо знати властивості графіка прямої на прикладі задач про вартість (додаток 4.5)
Суддя. Позивачі, чи задоволені ви роз’ясненнями наданими відповідачем ? Пропоную закрити слухання справи.
Розпорядник :Для оголошення вироку- встати .
Суддя : Вислухавши надані відповідачем аргументи на всі позови від студентів, справу оголошую закритою, оскільки позови задоволені. Судове слухання закрите.
Підсумок: (керівник гуртка)
На прикладі розглянутих задач слухачі математичного гуртка показали використання прямої у прикладних задачах економіки, фізики, транспорту.
Сподіваємося , що у всіх присутніх на сьогоднішньому відкритому засіданні гуртка зміниться ставлення до математики , як до строгої науки з її не завжди зрозумілими формулами, графіками , правилами; адже гуртківці змогли продемонструвати привабливість математики у таких повсякденних життєвих ситуаціях. Якщо хтось зацікавився, запрошуємо на наступні засідання гуртка, які будуть присвячені застосуванню прямої до рішення економічних задач математичного програмування.
ДОДАТКИ
.1 Рівняння з кутовим коефіцієнтом.
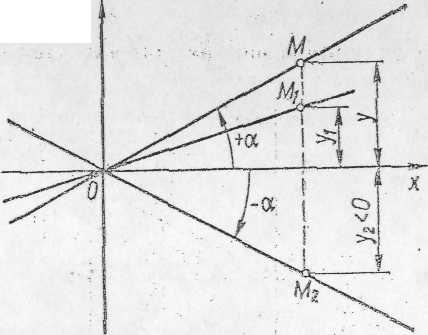
У рівнянні у=Кх, х і у є координатами довільної точки прямої, або, як їх образно називають, поточними координатами, а величина К = tg а характеризує пряму в цілому, визначаючи кут її нахилу до осі х. При цьому оскільки дві прямі утворюють між собою два різних кута, ми будемо розуміти під кутом нахилу а- кут, утворений додатнім напрямом прямої (тобто напрямом , що відповідає росту х), як це показано на мал. 1 стрілкою, і віссю Ох. Дослідимо, як змінюється х із зміною кута а. Для цього почнемо обертати пряму навколо нерухомої точки О, зменшуючи кут а, утворений прямою з додатним напрямком вісі х. Оскільки k не залежить від положення точки М на прямій, будемо цю точку брати весь час з однією і тією абсцисою х (рис.1). Тоді по мірі зменшення кута а зменшується і ордината у (у ![]()
![]()
![]()
Величина k, характеризує нахил прямої , називається кутовим коефіціентом прямої або її ухилом. Чисельно кутовий коефіціент К дорівнює tg a.
З алгебраїчної , або, як частіше кажуть, з аналітичної точки зору функція у=кх є функцією прямої пропорційності.
.2. Задача про ухил шляху.
На практиці часто використовують поняття ухил для того, щоб охарактеризувати положення прямої, тобто ступінь її нахилу до горизонтальної площини - К. Так, профіль шосейного або залізничного шляху можна повністю охарактеризувати, вказавши величини К і довжини ділянки, на якій К практично зберігає постійне значення. У межах кожної такої ділянки шлях вважаємо прямолінійним.
В якості прикладу накреслимо профіль шляху, визначений такими даними:
К=0,12 на ділянці 0 — 2,0 км
К = 0,20 » » 2,0 — 3,2 км
К = 0,05 » » 3,2 — 5,3 км
К = 0 » » 5,3 — 7,2 км
К = —0,1 » » 7,2 — 12,4 км
К = 0,16 » » 12,4 — 15,0 км
Для того, щоб накреслити першу ділянку, тобто провести пряму з ухилом К=0,12=12/100, відкладаємо від початку координат по осі Ох 100 довільних одиничних відрізків, у кінці цього відрізку відновлюємо перпендикуляр висотою в 12 таких же одиничних відрізків і отриману точку з’єднуємо з початком. Іншими словами , потрібно побудувати прямокутний трикутник з катетами 100 та 12 одиниць. Тоді його гіпотенуза буде мати ухил К=0,12 по відношенню до катета 100. Інші ділянки будуємо аналогічно. Весь профіль шляху показано на малюнку 2, причому додатнім значенням К відповідають підйоми ,а від’ємним К – спуски. При К = 0 шлях - горизонтальний.
3. Задачі, які розв’язуються за допомогою рівняння прямої.
Існує багато практичних задач, у яких досліджувані функції на заданому інтервалі з достатньою для практики точністю можна представити лінійними функціями, тобто можна розв’язувати за допомогою рівняння прямої. При цьому розглянемо більш узагальнений випадок, коли шукану функцію можна представити ламаною лінією, яка складається з декількох відрізків прямих.
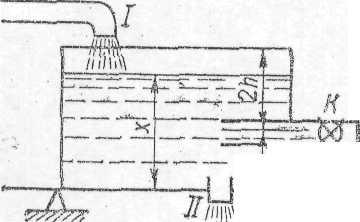
Задача. Вода наливається в басейн через трубу І зі швидкістю 3 одиниці в годину. По трубі ІІ вода витікає зі швидкістю 2,4 одиниці в годину. На висоті h від дна басейну розташована труба ІІІ із пропускною спроможністю 1,6 одиниці в годину,яку перекриває кран К і яка працює тільки 8 годин на добу( мал.3).
Потрібно дослідити режим рівня води Х в басейні , тобто виразити Х як функцію часу.
Розв’язання.
Режим роботи басейну можна охарактеризувати двома періодами: перший — при відкритому крані К (8 годин) та другим — при закритому крані К (16 годин).
Припустимо, що кран К відкривають в момент, коли басейн повний (Х=3h; t = 0). Тоді в перший період
Х = 3h - 3t — 2,4 t — 1,6t=- t + 3h , до Х=h, тобто до тих пір поки рівень води Х не досягне рівня h. Починаючи з цього моменту, для всього іншого часу першого періоду встановиться динамічна рівновага, так як при Х
По закінченню восьми годин , виключаємо трубу ІІІ . Починається другий період:
Х = h + 3 (t — 8) — 2,4 (t — 8) = 0,6 (t — 8) +h, до Х =3h.
Вище 3h рівень води піднятися не може , оскільки вода поллється через край.
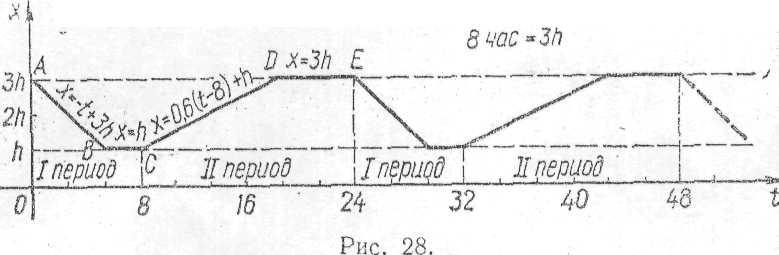
Все це показано графічно (рис.4) За цим графіком можна в будь-який момент часу t визначити , який рівень води в басейні.
З аналогічною задачею зіткнулися проектувальники Новокраматорського машинобудівного заводу.
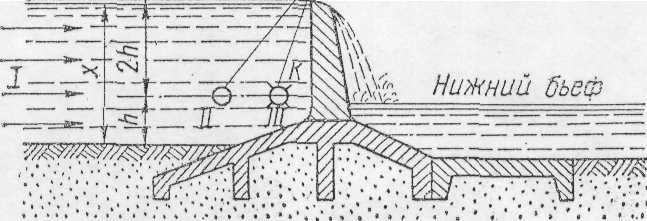
Завод, що споживає велику кількість води, треба було забезпечувати з невеликої річки, притоки Донця. Для того щоб «втамувати спрагу» цього гіганта в години найбільшого повного навантаження, на річці потрібно було спорудити греблю для цілодобового накопичення води, тобто спорудити «басейн» (мал.5), в якому труба І — кількість води, що надходить з течією річки, труба ІІ — втрати води на всмоктування (фільтрацію) в ґрунт під греблею та цілодобове обслуговування основних цехів заводу, труба ІІІ — зростання витрат води заводом при роботі на повну потужність в першу зміну. (Висота h необхідна для того, щоб водовідсосні турбини не засмоктували мул.)
З графіка режиму річки (рис. ) помічаємо два можливих неприємних моменти. У першому періоді, починаючи з моменту, що відповідає точці В, починає не вистачати води, а в другому періоді від точки D відбувається – безкорисний скид води.
4. Задача про розклад руху на залізничному транспорті.
Станції А і В сполучені одноколійним залізничним шляхом ( АВ= 28км). В 10км від станції А розташований полустанок Р. Зі станції А до станції В відходить поштовий потяг , час відправлення t = 10год 40хв; швидкість V=50км/год; з трьоххвилинною зупинкою на полустанку Р.
На дві хвилини пізніше на станцію А прибуває швидкій потяг , швидкість якого V=60км/год. Через скільки хвилин він повинен відправитися , щоб обігнати поштовий потяг саме на полустанку Р?
Крім того, зі станції В до станції А ,із зупинкою на полустанку Р, вирушає товарний потяг, швидкість якого V=54км/год. Треба побудувати графік безпечного руху потягів.
Спочатку побудуємо графік руху поштового потягу в системі координат t, S; де t – час руху в хвилинах, S – пройдений шлях в км; відповідно швидкість V = S /t вимірюється в км /хв. За початок відліку руху приймемо час t =10 год 40 хв. Тоді швидкість поштового потягу становитиме :
V= 50км/год=50/60 км/хв =5/6 км/хв.
Значить на перегоні АР шлях змінюється за законом S=5/6 t;
На полустанку Р S=10км =соnst протягом 3хв; На перегоні РВ S= 10 + 5/6 (t-3). Для графіка швидкого потягу S=V( t - t
Визначаємо t
t = 10год 54 в – 10год 40хв =14хв ; V=1км/хв. ; S= 10км. Підставивши відповідні дані в рівняння руху S= V(t- t
10год 40хв +4хв = 10год 44хв.
Товарний потяг повинен прибути на полустанок Р до моменту проходження його швидким потягом для того , щоб перегін РВ був вільним. Для врахування можливих помилок руху призначимо прибуття товарного на три хвилини раніше прибуття швидкого потягу, тобто для товарного потягу маємо V=54км/год=0,9км/хв.; S= РВ=18км;
t=10год 51хв - 10год 40хв = 11хв, тоді 18=0,9(11- t
t
Отже товарний потяг повинен вирушити зі станції В до станції А на 9 хвилин раніше, тобто в 10год31хв, відправитись після зупинки на полустанку він зможе зразу ж після проходження швидкого потягу - в 10год 54хв.
4.5. Застосування лінійної функції для розв’язування задач з економіки
Серед соціальних наук - економіка найбільшою мірою використовує математику. Математичні моделі, як правило, ускладнюються поетапно з урахуванням послідовного зменшення кількості обмежень при розв'язанні конкретних задач, що виникають у процесі навчання як майбутніх студентів-економістів. Особлива роль відводиться задачам, які демонструють застосування різних розділів математики в соціальних науках. Проілюструємо вищезгадане на розв'язанні окремих конкретних задач мікро- та макроекономіки.
Нагадаємо, що мікроекономіка аналізує діяльність окремих ланок господарської системи. Це можуть бути окремі фірми, підприємства, ринки конкретних видів товарів та послуг тощо. При цьому одне з важливих питань мікроекономіки полягає у вивченні взаємодій попиту та пропозицій. Попит на даний товар — це потреба у певній кількості товару, яка обмежена діючими цінами і платоспроможністю споживачів. Пропозицію можна визначити як кількість товару, який може бути запропоновано на ринку для продажу за певною ціною.
Інтуїтивно очевидно, що випуск додаткової продукції потребує додаткових витрат. Щоб спонукати до цього виробника, потрібно запропонувати йому підвищену ціну, тобто пропозиція є деякою функцією ціни. Якщо позначити пропозицію через S а ціну через Р, то сказане може бути записане у вигляді: S=f (P).
Ця функція може бути досить складною, і, крім того, пропозиція S може залежати не лише від ціни на товар Р, а й від інших факторів. Ми, свідомо, цими факторами зараз нехтуємо. В економіці графік залежності пропозиції від ціни називається кривою пропозиції. Оскільки будь-якій функції на координатній площині відповідає деяка крива лінія, слово «крива» у даному випадку просто є синонімом «графіка функції». Крім того, економісти, як правило, незалежну змінну відкладають на вертикальній осі координат, а значення функції S— на горизонтальній. Традиція є традиція, і ми будемо наслідувати. Проте якщо пропозиція S залежить від ціни, то навпаки, ціна Р залежить від пропозиції S це можливо записати у вигляді:
Р= g (S), де g - функція, називається оберненою відносно f.
Наприклад. Якщо у = 2х — 4, то дістанемо обернену функцію: х = 0,5y + 2.
Записана у формі Р = g (S) крива пропозиції вказує лише на існування зв'язку між Р і S.
Конкретний вигляд цієї залежності може бути отриманий або з емпіричних даних, або з економічної теорії. Ми, однак, зробимо припущення, що цю залежність можна подати найбільш простою, а саме лінійною функцією:
Р= аS+ b, де а і b— деякі сталі величини, що називаються параметрами, визначаються емпірично.
Зрозуміло, наше припущення про лінійну залежність цін від пропозиції S є великим спрощенням дійсності. Проте, по-перше, лінійна функція найбільш проста і аналізувати її легше за все, по-друге, це дає нам можливість хоча б дещо наблизитися до розв'язання задачі. Такий прийом, при якому ми визначаємо деякі суттєві риси з реальної задачі, а потім робимо спрощення, припущення, дістав назву «моделювання».
Реальність «заміняємо» певною моделлю, досліджуючи яку ми можемо робити передбачення. Чим ближче модель до дійсності, тим вона складніша і тим точніше передбачення, яке можна зробити за її допомогою.
Економічна теорія (і здоровий глузд) підказують, що пропозиція товару зростає зі збільшенням ціни. Дійсно, чим вища ціна на товар, тим більше число виробників намагаються запропонувати цей товар на ринку. Це, в свою чергу, означає, що функція є Р= аS+ в є зростаючою, тобто а > 0 (мал.1).
Займемося зараз вивченням кривої попиту. На відміну від кривої пропозиції вона є спадаючою функцією. Дійсно, якщо ціна на якийсь товар зростає, то і кількість реалізованого товару зменшуватиметься. Можна сміливо стверджувати, що автомобілів класу «Деу-ланос» у нас реалізується більше, ніж автомобілів «Ролс-Ройс».
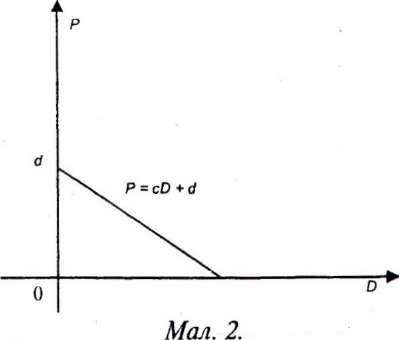
Припустимо далі, що криву попиту можна у першому наближенні також подати прямою лінією. Тоді, описуючи спадну функцію, крива попиту може бути записана у вигляді:
Р= сD +d, с< 0,
де Р — ціна, D — попит, а с і d— сталі величини, тобто параметри. Як і для кривої пропозиції, ми користуємось оберненою функцією, тобто подамо ціну Р через попит D, а не навпаки, віддаючи належне економічній традиції.
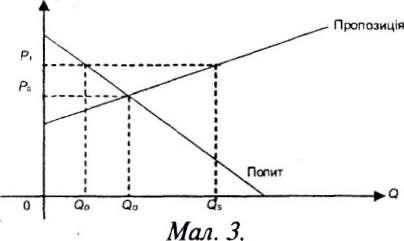
Попит і пропозиція стосуються певного товару або групи товарів. Кількість товару залежно від виду може вимірюватись у різних одиницях: автомобілі у штуках, нафтопродукти у тоннах і т.ін. Для нас, однак, важливо, щоб ці одиниці для попиту і пропозиції були одні й ті самі. Тому, зображаючи кількість товару буквою Q, ми можемо криві попиту і пропозиції зобразити на одному графіку (мал. 3).
У мікроекономіці виникає інтерес — точка перетину кривих попиту і пропозиції. Ця точка називається точкою рівноваги, а відповідна їй ціна — рівноважна ціною. Такі назви пов'язані з тією обставиною, що в точці рівноваги попит приходить у відповідність з пропозицією, тобто увесь вироблений товар знаходить свого покупця, і всі бажаючі придбати даний товар мають змогу це зробити. Не менше ніж рівноважна ціна викликає інтерес відхилення ринкової ціни від рівноважної.
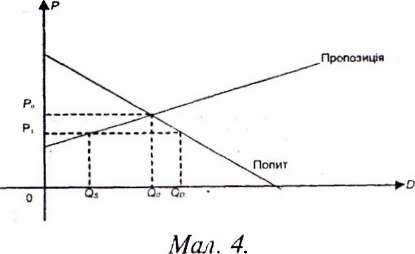
Звернемось до мал. 3. З нього видно, що якщо ринкова ціна Р1 більше рівноважної ціни Р0, кількість товару QS, що відповідає пропозиції, більше кількості товару Qр, що відповідає попиту, тобто пропозиція перевищує попит. Як наслідок — надлишок нереалізованої продукції на складах. У свою чергу це буде спонукати виробників зменшити ціну на продукцію, тобто ринкова ціна Р1 прямуватиме до рівноважної ціни Р0. Це явище відоме як «тиск ринку».
Припустимо, що ринкова ціна Р1 менша рівноважної ціни Р0. З мал. 4 маємо, що у цьому випадку кількість товару QS що відповідає ринковій ціні Р1, менша кількості товару QD, що відповідає тій самій ринковій ціні Р1. Це, в свою чергу, означає, що попит перевищує пропозицію. У такій ситуації виробники товару, користуючись дефіцитом,
підвищують ціну, тобто ринкова ціна знову прямує до рівноважної ціни Р0.
Необхідно ще раз підкреслити, що модель, яку ми щойно розглянули, сильно спрощує дійсність. По-перше, вона містить припущення про лінійність кривих (функцій) попиту і пропозиції. По-друге, попит і пропозиція залежать не лише від ціни, а й від ряду інших факторів. Це, в свою чергу, потребує використання складнішого та вдосконалішого математичного апарату, зокрема, теорії функцій багатьох змінних.
Використані джерела
- Слєпкань З.І. Методика навчання математики.- К:Вища шк.,2006.- 582с. р.9 с.143-147
- Колягин Ю.М. Методика преподавание математики в средней школе .- М:Просвещение ,1975 .-462с. с.336-344
- Гусев В.А. Внеклассная работа по математике в 6-8 классах. М:Просвещение ,1997.-288с. Т.5,с.18, Т.11, с.41-48
- Березин В.Н. Сборник задач для факультативных и внеклассных занятий по математике.М.:Просвещение, 1985.- 175с., с141-150
- У світі математики , випуск 7, К.:- Радянська шк..,1076.- 228с., с23-35
- Математика в школі ,10.2010- с.22-26
- Математика в школі,11.2010- с.3-4
- Квант,11.1974 - с.48-53.

 Получите свидетельство
Получите свидетельство Вход
Вход



 Верхній бьєф річки Водовідсосні турбіни
Верхній бьєф річки Водовідсосні турбіни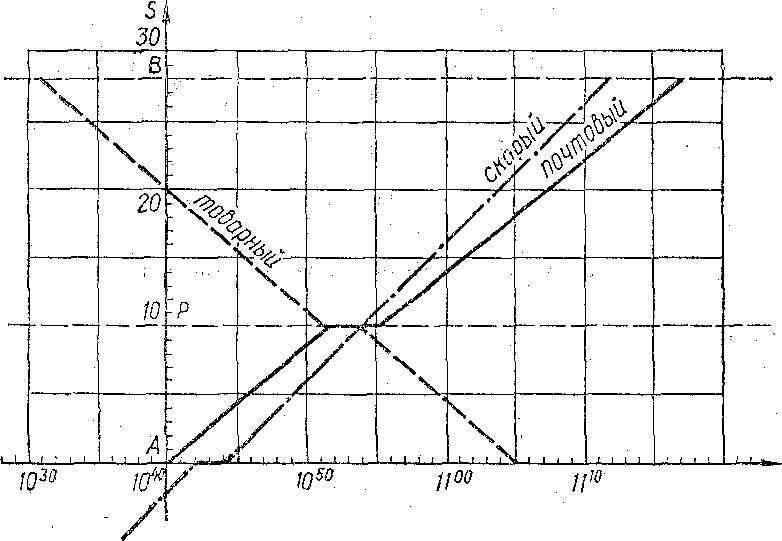 Мал. 6
Мал. 6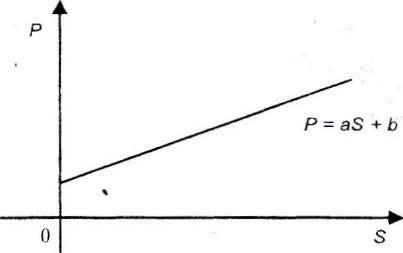









 Пряма в прикладних задачах (0.26 MB)
Пряма в прикладних задачах (0.26 MB)
 0
0 419
419 52
52 Нравится
0
Нравится
0


