1. Найдите значение выражения ![]()
2. Найдите значение выражения ![]()
3. Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 22 500 рублей. Какую сумму он получит после уплаты налогов? Ответ дайте в рублях.
4. Найдите v0 из равенства v = v0 + at, если v = 20 , t = 2 и a = 7.
5.
Найдите значение выражения ![]() .
.
6. Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
7. Найдите корень уравнения ![]()
8. 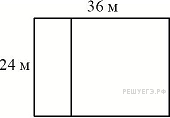 Дачный участок имеет форму прямоугольника со сторонами 24 метра и 36 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите общую длину забора в метрах.
Дачный участок имеет форму прямоугольника со сторонами 24 метра и 36 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите общую длину забора в метрах.
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ |
| ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
| А) высота железнодорожного вагона Б) высота небоскреба В) высота гриба-подосиновика Г) размер неровностей на поверхности стекла |
| 1) 3,5 м 2) 10 см 3) 120 м 4) 0,5 мкм |
10. Игральную кость с 6 гранями бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.
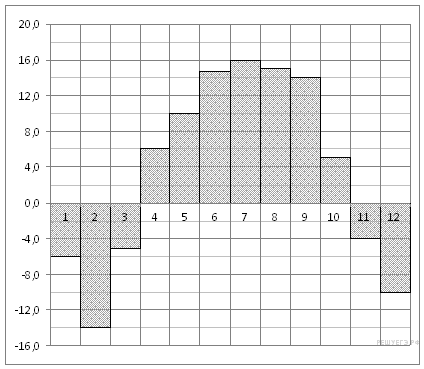
11. На диаграмме показана среднемесячная температура в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия.
12. В трёх салонах сотовой связи один и тот же телефон продаётся в кредит на разных условиях. Условия даны в таблице.
| Салон | Цена телефона (руб.) | Первоначальный взнос (в % от цены) | Срок кредита (мес.) | Сумма ежемесячного платежа (руб.) |
| Эпсилон | 15 400 | 25 | 12 | 1390 |
| Дельта | 16 200 | 5 | 6 | 3240 |
| Омикрон | 16 000 | 25 | 12 | 1350 |
Определите, в каком из салонов покупка обойдётся дешевле всего (с учётом переплаты). В ответе запишите эту сумму в рублях.
13. 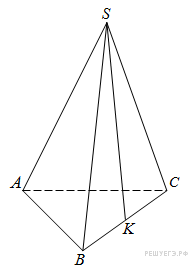 В правильной треугольной пирамиде SABC точка K – середина ребра BC, S – вершина. Известно, что SK = 4, а площадь боковой поверхности пирамиды равна 54. Найдите длину ребра AC.
В правильной треугольной пирамиде SABC точка K – середина ребра BC, S – вершина. Известно, что SK = 4, а площадь боковой поверхности пирамиды равна 54. Найдите длину ребра AC.
14. На графике показана зависимость крутящего момента автомобильного двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту. На оси ординат — крутящий момент в H · м.
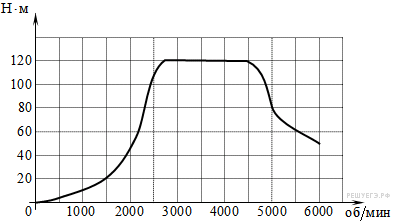
Пользуясь графиком, поставьте в соответствие каждому интервалу количества оборотов двигателя характеристику зависимости крутящего момента двигателя на этом интервале.
| ХАРАКТЕРИСТИКИ ПРОЦЕССА |
| ИНТЕРВАЛЫ ОБОРОТОВ |
| А) крутящий момент не менялся Б) крутящий рос быстрее В) крутящий момент падал Г) крутящий момент не превышал 20 H · м |
| 1) 0 − 1500 об/мин. 2) 2000 − 3000 об/мин. 3) 3000 − 4000 об/мин. 4) 4000 − 6000 об/мин. |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б | В | Г |
|
|
|
|
|
15. 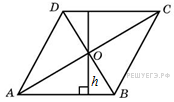 Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
16. 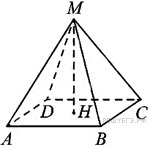 Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно ![]() .
.
17. Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
| ЧИСЛА |
| ОТРЕЗКИ |
| А) Б) В) Г) |
| 1) [1;2] 2) [2;3] 3) [3;4] 4) [5;6] |
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
| А | Б | В | Г |
|
|
|
|
|
18. В посёлке городского типа всего 12 жилых домов. Высота каждого дома меньше 30 метров, но не меньше 9 метров. Выберите утверждения, которые следуют из данной информации.
1) В посёлке есть жилой дом высотой 30 метров.
2) Разница в высоте любых двух жилых домов посёлка больше 3 метров.
3) В посёлке нет жилого дома высотой 8 метров.
4) Высота любого жилого дома в посёлке не меньше 7 метров.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Найдите трехзначное натуральное число, большее 600, которое при делении на 4, на 5 и на 6 дает в остатке 3, и цифры которого расположены в порядке убывания слева направо. В ответе укажите какое-нибудь одно такое число.
20. В корзине лежит 50 грибов: рыжики и грузди. Известно, что среди любых 28 грибов имеется хотя бы один рыжик, а среди любых 24 грибов хотя бы один груздь. Сколько груздей в корзине?

 Получите свидетельство
Получите свидетельство Вход
Вход











 Проверочная работа (Базовый уровень) (101 KB)
Проверочная работа (Базовый уровень) (101 KB)
 0
0 781
781 14
14 Нравится
0
Нравится
0






