1. Назначение работы – оценить подготовку по математике студентов 1 курса СПО по теме: «Связь между свойствами функции и графиком».
2. Документы, определяющие содержание работы.
Содержание работы определяется на основе следующих документов:
Обязательный минимум содержания среднего (полного) общего образования по предмету (Приказ Минобразования России № 56 от 30. 06. 1999 г. ) ;
Федеральный компонент государственного стандарта общего образования. Математика (Приказ Минобразования России № 1089 от 05. 03. 2004 г. ).
Программы для общеобразовательных школ, гимназий, лицеев: Математика. 5-11 кл. / Сост. Г. М. Кузнецова, Н. Г. Миндюк. – М. : Дрофа, 2000, 2002.
Примерные программы вступительных экзаменов (испытаний) в высшие учебные заведения Российской Федерации / Автор-составитель Г. В. Арсеньев и др. – М. : Высш. шк., 2000;
Оценка качества подготовки выпускников основной школы по математике / Г. В. Дорофеев и др. – М. : Дрофа, 2000;
Оценка качества подготовки выпускников средней (полной) школы по математике / Г. В. Дорофеев и др. – М. : Дрофа, 2002;
3. Условия применения.
Работа рассчитана на студентов 1 курса СПО, изучивших курс математики, отвечающий обязательному минимуму содержания среднего (полного) общего образования по математике.
4. Структура работы.
Работа состоит из 15 заданий, которые различаются по назначению, а также по содержанию, сложности, числу и форме включаемых в них заданий.
1, 2, 4, 5, 8-10, 12, 13 задания – с выбором ответа (из предложенных);
3, 11 задания – с кратким ответом (в виде целого числа или числа, записанного в виде десятичной дроби или в виде графика);
6, 7, 15 задания - с развернутым ответом (запись решения);
14 задание – с развернутым ответом (полная запись решения с обоснованием).

5. Время выполнения работы.
На выполнение работы отводится 45 минут (1 урок).
6. Система оценивания выполнения отдельных заданий и работы в целом.
Верное выполнение заданий базового уровня (1, 2, 4, 5, 8-10, 12, 13 задания) и повышенного уровня с кратким ответом (3, 11 задания) оценивается 1 баллом. Выполнение задания с развернутым ответом повышенного уровня (6, 7, 15 задания) в зависимости от полноты и правильности ответа оценивается от 0 до 2 баллов.
Выполнение задания с развернутым ответом высокого уровня (14 задание) в зависимости от полноты и правильности ответа оценивается от 0 до 4 баллов.
Таким образом, за верное выполнение всех заданий теста можно максимально получить 21 балл.
Отметка за выполнение работы определяется по 5-балльной шкале.
«2» - 0- 7 баллов
«3» - 8-14 баллов
«4» - 15-18 баллов
«5» - 19-21 балл
7. Дополнительные материалы и оборудование
Не используются. Использование калькуляторов не разрешается.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



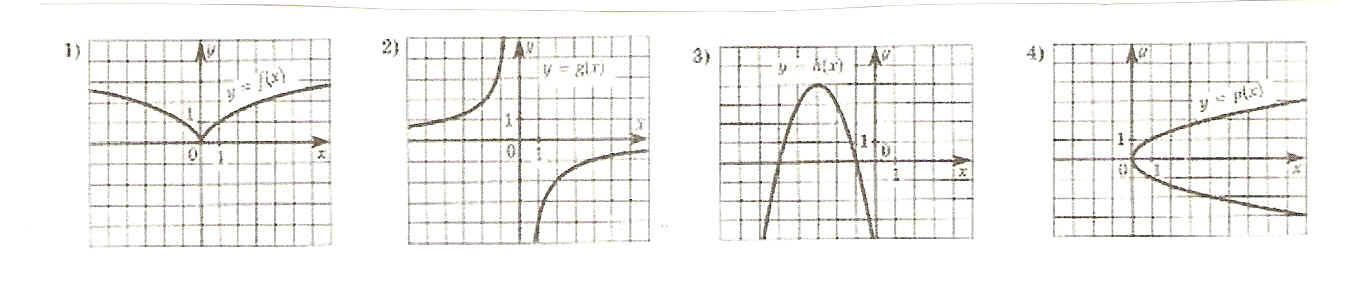
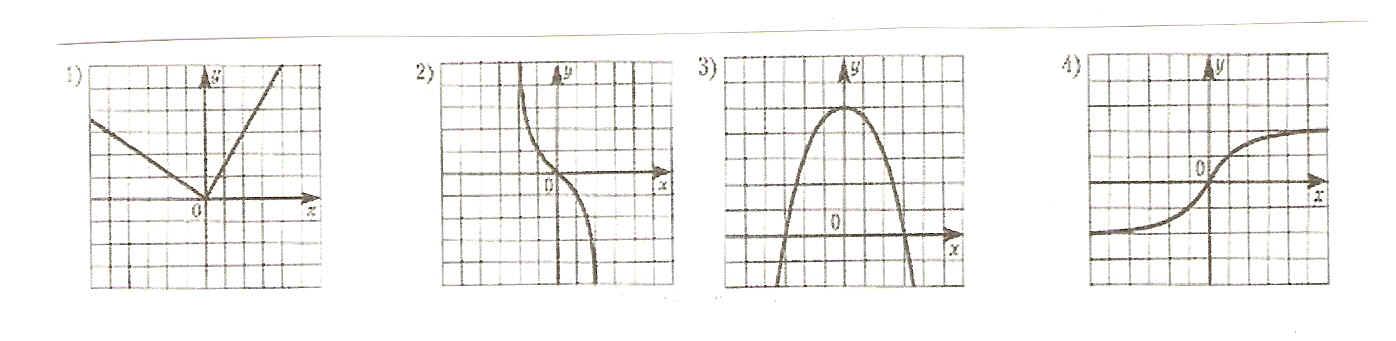
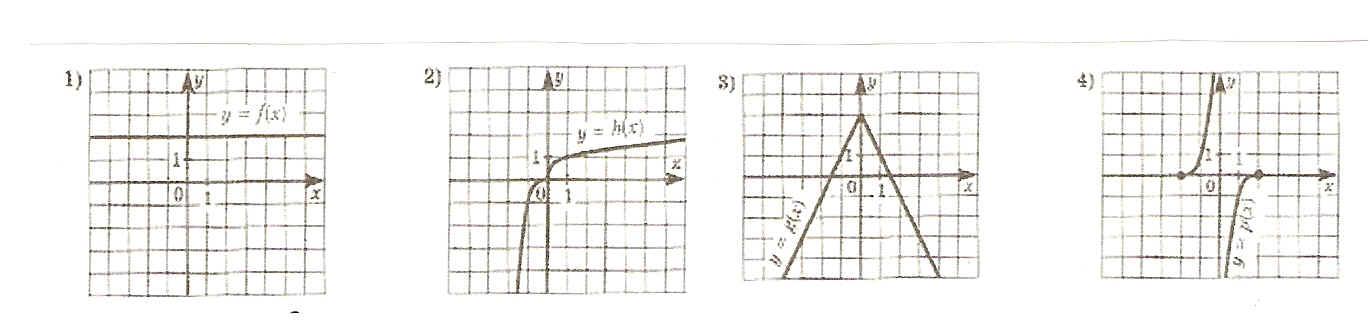
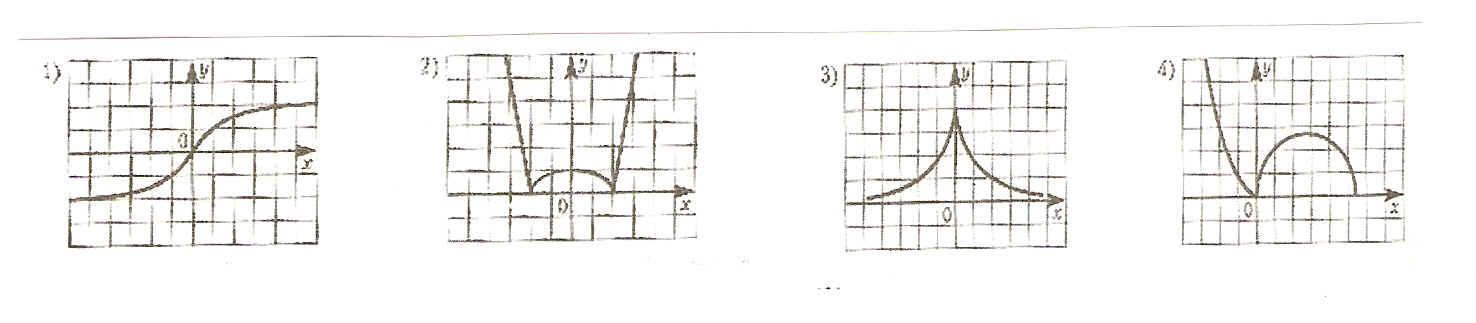
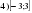
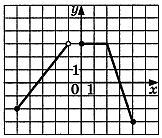
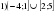
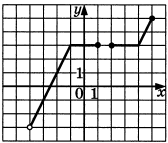
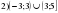
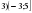
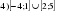
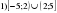
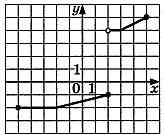
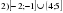
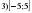
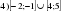
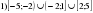









 Проверочная работа по математике «Связь между свойствами функции и графиком» (0.48 MB)
Проверочная работа по математике «Связь между свойствами функции и графиком» (0.48 MB)
 0
0 833
833 51
51 Нравится
0
Нравится
0




