Программа курса по математике "Математика на компьютере"

Курс по выбору "Математика на компьютере", включающий одну из тем "Решение систем линейных уравнений", предназначен для учащихся 9 класса (предпрофильное обучение). Курс рассчитан на 16 часов.

Предварительный уровень подготовки: знание основ решения систем линейных уравнений, знание основ аппаратного обеспечения персональных компьютеров, применение компьютерных технологий для решения математических задач, знание основ алгоритмизации и программирования.

Курс предполагает познакомить учащихся с новыми методами решения систем линейных уравнений (Метод Крамера, Метод Гаусса), с применением ПК.

Курс поможет учащемуся оценить свой потенциал с точки зрения образовательной перспективы, поможет ученику проверить себя, ответить на вопросы: "Могу ли я, хочу ли я учить это, заниматься этим?".

Курс будет полезен ученику для совершения осознанного выбора профиля обучения в старшей школе, так как включает показ специфики данного профиля через практическую исследовательскую деятельность, поисковую деятельность, анализ с применением компьютерных технологий.

Данный курс не дублирует базовый курс.

Преподавание данного курса будет проводиться при наличии УМК: учебное пособие "Алгебра и начала анализа 9 - 10" под редакцией А. Н. Колмогорова, Москва: "Просвещение", 1983 г., п. 73. Решение систем линейных уравнений, стр. 224 - 228; справочник по элементарной математике под редакцией М. Я. Выгодского, Москва "Наука", Главная редакция физико-математической литературы, 1978 г., лабораторные работы с применением ЭТ, средства программирования. В обучении можно использовать программно - методический пакет по математике Maple.

Динамика интереса к курсу будет идти через интеграцию обучения (математика + информатика).

Форма отчётности - решение учеником систем линейных уравнений разными методами, которые он освоил и умеет применить (зачётная система).

Цель курса:

формирование у учащихся практических умений в применении компьютерных технологий, позволяющих исследовать нестандартные методы решения систем линейных уравнений.

Задачи курса:

Формирование у учащихся ключевых компетентностей в области математики и информатики.

Развитие у учащихся интеллектуальных и практических умений и навыков в области математики.

Реализация творческих исследовательских умений школьников в программировании.

Построение индивидуальных траекторий образовательного пути учащихся в области математики.

Оказание учащимся педагогической поддержки в проектировании и выборе направления дальнейшего обучения.

Тематическое планирование.

Весь материал - в документе.

Рассмотрено на заседании ШМО учителей естественно – математического цикла Руководитель ШМО: Е.С. Сапожникова Протокол № ___ от «____»___________2014 г.

Согласовано на заседании методического совета протокол № ___ от_____2014 г. Утверждено на заседании Управляющего совета протокол № ___ от _____2014 г.

Программа курса по выбору

" Математика на компьютере"

с элементами информатики

для учащихся 9 класса средней школы

(в рамках предпрофильного обучения)

(16 часов)

Учитель математики и информатики: Сапожникова Елена Семеновна

2014-2015 учебный год

Содержание

1. Пояснительная записка	3
2. Тематическое планирование	5
3. Приложение. Краткие рекомендации по изучению курса	7
4. Литература	18

Пояснительная записка

Курс по выбору "Математика на компьютере", включающий одну из тем "Решение систем линейных уравнений", предназначен для учащихся 9 класса (предпрофильное обучение). Курс рассчитан на 16 часов.

Предварительный уровень подготовки: знание основ решения систем линейных уравнений, знание основ аппаратного обеспечения персональных компьютеров, применение компьютерных технологий для решения математических задач, знание основ алгоритмизации и программирования.

Курс предполагает познакомить учащихся с новыми методами решения систем линейных уравнений (Метод Крамера, Метод Гаусса), с применением ПК.

Курс поможет учащемуся оценить свой потенциал с точки зрения образовательной перспективы, поможет ученику проверить себя, ответить на вопросы: "Могу ли я, хочу ли я учить это, заниматься этим?".

Курс будет полезен ученику для совершения осознанного выбора профиля обучения в старшей школе, так как включает показ специфики данного профиля через практическую исследовательскую деятельность, поисковую деятельность, анализ с применением компьютерных технологий.

Данный курс не дублирует базовый курс.

Преподавание данного курса будет проводиться при наличии УМК: учебное пособие "Алгебра и начала анализа 9 - 10" под редакцией А. Н. Колмогорова, Москва: "Просвещение", 1983 г., п. 73. Решение систем линейных уравнений, стр. 224 - 228; справочник по элементарной математике под редакцией М. Я. Выгодского, Москва "Наука", Главная редакция физико-математической литературы, 1978 г., лабораторные работы с применением ЭТ, средства программирования. В обучении можно использовать программно - методический пакет по математике Maple.

Динамика интереса к курсу будет идти через интеграцию обучения (математика + информатика).

Форма отчётности - решение учеником систем линейных уравнений разными методами, которые он освоил и умеет применить (зачётная система).

Цель курса: формирование у учащихся практических умений в применении компьютерных технологий, позволяющих исследовать нестандартные методы решения систем линейных уравнений.

Задачи курса:

1. Формирование у учащихся ключевых компетентностей в области математики и информатики.

2. Развитие у учащихся интеллектуальных и практических умений и навыков в области математики.

3. Реализация творческих исследовательских умений школьников в программировании.

4. Построение индивидуальных траекторий образовательного пути учащихся в области математики.

5. Оказание учащимся педагогической поддержки в проектировании и выборе направления дальнейшего обучения.

Тематическое планирование

№	Содержание	Кол - во часов	Цель	Теоретич. часть (основн. понятия)	Практич. часть	Форма отчётности
1	Введение в тему "Системы лин. ур."	3	Обобщение и диагностика уровня знаний, полученных в базовом курсе	Линейное уравнение. Решение лин.ур. Равносильные уравнения. Системы лин. ур. Равнос. сист. ур. Решение систем лин. уравнений. Суть методов решения систем лин.уравнений (подстановка, сложение, графический способ).	Практикум по решению систем лин. уравнений разными методами	Решение в тетради
2	Графическая интерпретация систем лин. ур. с двумя переменными	2	Формирование у учащихся умений использовать комп. технологии в учебном процессе	Что значит графически решить сист. уравнений? График лин. ур. Когда система имеет одно реш., не имеет реш., имеет бесконечно много решений?	Лаборат. работа - использование ЭТ для граф. реш. систем лин. ур..	Вывод решения систем на бумагу и анализ результатов
3	Системы линейных ур. с двумя перем. с параметром	2	Развитие умения нестандартно мыслить через нестандартные задания	Угловой коэффициент прямой. Параметр.	Исследование систем лин. ур. с параметром. Для конкрет- ных систем найти ответы на вопросы: При каком знач. параметра a сист. имеет бесконечно много реш., не имеет реш., имеет одно решение?	Отчёт о решении в тетради и на ПК.
4	Правило Крамера	1	Ознакомить учащихся с выводом формул Крамера и их практическим применен. при реш. сист. лин.ур..	Определитель второго порядка. Формулы Крамера.	Исследование формул Крамера. Поиск в Интернете сведений о жини и деятельности Крамера в области математики.	Отчёт о выводе формул и решение систем в тетради.
5	Метод Крамера. Задача программирования на ЭВМ решения системы лин. ур.с двумя неизвестными.	2	Побудить учащихся к творческому нестандарт-ному мышлению через нестандартные вопросы и задания. Реализация творческих исследоват-х умений школьников в программир - и.	Алгоритм, блок - схема, алгоритмические структуры.	Разработка алгоритма решения систем лин. ур. методом Крамера и программы на языке программирования QBASIC, реализация на ЭВМ.	Отчёт о решении систем лин. уравнений на ПК.
6	Метод Гаусса	4	Выработка умений применять метод Гаусса при решении систем лин. ур. с 2 неизвестными, с 3 неизвестными, с N незивестн.	Суть метода Гаусса. Применение метода Гаусса в геодезии.	Лабораторная работа по готовому алгоритму (решение систем из 3 лин уравнений). Исследова-тельская работа по разработке алгоритма решения системы из N лин.уранен. Программи-рование на ЭВМ метода Гаусса.	Отчёт о решении систем лин. уравнений методом Гаусса в тетради и на ПК.
7	Итоговое занятие	2	Повторение и обобщение по применению новых методов решения систем линейных уравнений. Контроль знаний.	Повторить идеи новых методов решения систем линейных уравнений.	Самост. раб. - решение систем линейных уравнений разного уровня сложности	Отчёт о решении в тетради и на ПК.
	Всего	16

Приложение

Краткие рекомендации по изучению курса

Сначала учащимся предлагается вспомнить: какое уравнение называется линейным, что называют решением линейного уравнения, какие уравнения называются равносильными, что представляет собой система линейных уравнений, что является решением системы двух линейных уравнений с двумя неизвестными, какие системы уравнений называются равносильными; три метода решения систем линейных уравнений: метод сложения, метод подстановки, графический метод (при этом вспомнить правила - замены, подстановки, сложения). Приводятся примеры решения систем линейных уравнений. Возможно использование компьютерных информационных технологий: ЭТ и специальных пакетов.

Графический способ решения систем линейных уравнений полезно выполнить с помощью ЭТ на компьютере.

Пусть заданы следующие системы линейных уравнений:

1









. 7х - 3 = у 2. у = 7х - 3 3. у + 3 = 7х 4. -3 +7х = у

у = - 2х - 6 5х + 4 = у у = 7х + 4 х - 0, 3 = у

Каждое из уравнений в представленных четырёх системах может быть записано в виде функции:

f = y(x).

Очевидно, что первое уравнение в каждой из систем описывается функцией

f = 7x - 3.

Остальные уравнения описываются функциями f_i , где i отвечает порядковому номеру системы:

f1 = -2x - 6;

f2 = 5x +4;

f3 = 7x +4;

f4 = x - 0, 3.

Для графического решения заданных систем уравнений выполните следующие шаги:

1. Создайте шапку таблицы со столбцами x, f1, f2, f3, f4.

2. Заполните столбец x значениями из интервала [ -6; 6] с шагом 1.

3. Запишите в первую строку столбцов f1, f2, f3, f4 соответствующие формулы и скопируйте их в остальные ячейки столбцов.

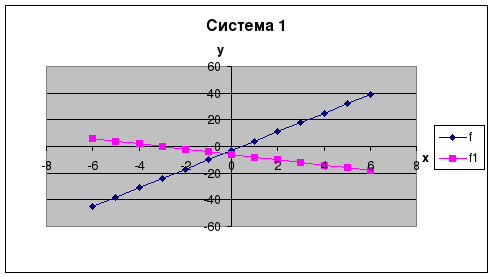
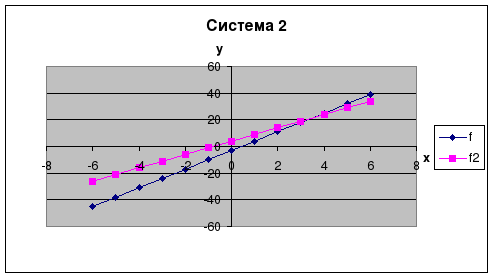
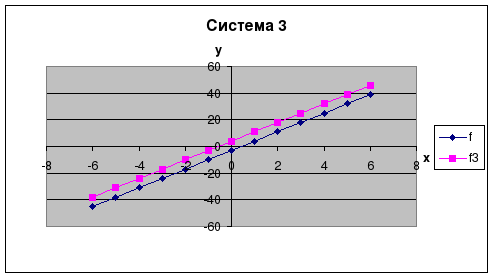
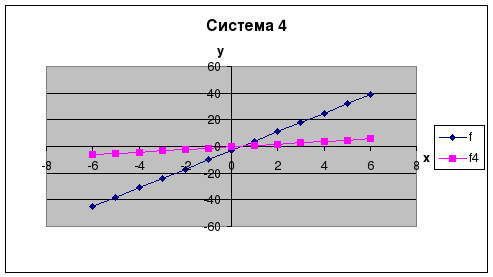
4. Составьте диаграммы для первой системы линейных уравнений на основе данных столбцов x, f, f1 и для второй системы - на основе данных столбцов x, f, f2. Аналогичным образом постройте диаграммы для третьей и четвёртой систем, используя данные столбцов x, f, f3; x, f, f4.

5. Рассмотрите графики функций и проанализируйте полученные решения систем.

Для проверки - результаты выглядят так: (см ниже)

    Графическое решение линейных систем уравнений
1. Y= 7x - 3 2. Y= 7x - 3 3. У= 7х -3 4. У= 7х - 3
Y=-2x - 6 Y= 5x + 4 У= 7х + 4 У= х - 0, 3
x	f	f1	f2	f3	f4
-6	-45	6	-26	-38	-6,3
-5	-38	4	-21	-31	-5,3
-4	-31	2	-16	-24	-4,3
-3	-24	0	-11	-17	-3,3
-2	-17	-2	-6	-10	-2,3
-1	-10	-4	-1	-3	-1,3
0	-3	-6	4	4	-0,3
1	4	-8	9	11	0,7
2	11	-10	14	18	1,7
3	18	-12	19	25	2,7
4	25	-14	24	32	3,7
5	32	-16	29	39	4,7
6	39	-18	34	46	5,7

С помощью ЭТ предложить учащимся решить более сложные системы линейных уравнений графическим методом. Например,







А) 7x - 2y = -1 B) 2x + 3y = -1 C) x + 1,5y = 4

3x - 5y = 12 5x + 4y = 1 4x + 6y = 3, 7

и другие.

При исследовании систем линейных уравнений с двумя переменными учащиеся с помощью компьютера получают геометрическую интерпретацию и делают вывод.

Вывод: линейные уравнения системы определяют две прямые на плоскости. Они либо пересекаются, либо параллельны и не имеют общих точек, либо параллельны и совпадают.

Д



алее полезно рассмотреть решение задачи следующего типа: при каком значении параметра а система

х + у = 1

а х - 2у = 3

имеет решение?

Ответ: при а  - 2.

Можно предложить решить учащимся следующие упражнения:

П





ри каком значении параметра а система имеет бесконечно много решений?

А) х + а у = 2 Б) х + 1, 5 у = 4

3х - 2у =6 4х + 6у = а

П







ри каком значении параметра а система не имеет решений?

А) 2х + ау = 8 Б) х - у = 2 В) х - у = 3

3х - 5у = 6 2х - 2у = а ах + 2у = -6

Можно ли указать значение параметра а, при котором система имеет решение?







А) х - 5у = 7 Б) х + 2у = а В) 3х - 2у = 6

ах + у = -3 2х +4у =5 ах +у = -3

В число задач, которые следует обязательно проработать на занятиях элективного курса, входит задача программирования решения на ЭВМ систем линейных уравнений. Система линейных уравнений является математической моделью многих прикладных задач, и умение грамотно работать с такой моделью необходимо.

Целесообразно начать с решения системы двух линейных уравнений с двумя неизвестными и вместе с учащимися разобрать использование формул Крамера, введя понятие об определителе второго порядка. В последнее время этот метод не включается в число обязательных для изучения на уроках математики в базовом курсе.



Систему можно записывать в виде, удобном для дальнейшего программирования:

а₁₁х₁ +а₁₂х₂= а₁₃

а₂₁х₁ +а₂₂х₂= а₂₃

Преподаватель вводит понятия об определениях системы и двух вспомогательных определителях. Сделать это целесообразно, рассмотрев решение данной системы методом алгебраического сложения.



Приводим соответствующие выкладки:

а₁₁х₁ +а₁₂х₂= а₁₃ умножаем обе части уравнения на а₂₂

а₂₁х₁ +а₂₂х₂= а₂₃ умножаем обе части уравнения на а₁₂



а₁₁ а₂₂ х₁ +а₁₂ а₂₂ х₂= а₁₃ а₂₂

а₂₁ а₁₂ х₁ +а₂₂ а₁₂ х₂= а₂₃ а₁₂ (вычитаем одно уравнение из другого)

(а₁₁ а₂₂ - а₂₁ а₁₂) х₁= а₁₃ а₂₂ - а₂₃ а₁₂

Аналогично получаем

(а₁₂ а₂₂ - а₂₁ а₁₂) х₂= а₁₃ а₂₁ - а₂₃ а₁₁

Вводим обозначения:

D = а₁₁ а₂₂ - а₂₁ а₁₂

D_x1 = а₂₂ а₁₃ - а₂₃ а₁₂

D_x2 = а₁₃ а₂₁ - а₂₃ а₁₁

О

D_x1

D_x2

тсюда получаем формулы Крамера для вычисления х₁ и х₂:

D

D

х₁ = ; х₂ =

После таких разъяснений составляется схема алгоритма реше­ния системы двух линейных уравнений с двумя неизвестными. При этом обращается внимание на роль определителя системы D; подчеркивается, что если D=0, то система единственного решения не имеет.

Разработка программы может стать темой практического занятия для всего класса в целом (схема алгоритма должна быть у каждого учащегося или в виде плаката на стене).

Приводим возможный вариант текста программы:

CLS

REM Решение систем линейных уравнений

DIM A (2, 3)

FOR I = 1 TO 2

FOR J =1 TO 3

INPUT A (I, J)

NEXT J

NEXT I

D = A (1, 1) * A (2, 2) - A (2, 1) * A (1, 2)

IF D =0 THEN PRINT "единственного решения нет": END

Dx = A (1, 3) * A (2, 2) - A (2, 3) * A (1, 2)

Dy = A (1, 1) * A (2, 3) - A (2, 1) * A (1, 3)

X = Dx / D: Y = Dy / D

PRINT X, Y

END

Решите системы и проверьте найденные корни:





А) 5х - 3у = 16 Б) 9, 21х - 5, 41у = 34,1436

7х + 2у = 41 17, 39х + 11, 56у = 47, 0372

Для закрепления темы рекомендуется приготовить карточки - задания. В карточках - заданиях можно затронуть проблему значительного влияния на решение точности вводимых коэффициентов, особенно если определитель близок к нулю.

Школьникам следует пояснить, что в этом случае небольшое изменение коэффициентов может значительно изменить величину искомых корней. Полезно все рассуждения иллюстрировать геометрически.

Более практичные методы решения линейных систем предложил К. Ф. Гаусс (1777 - 1855). По методу Гаусса вычислители могли за день работы решить систему с десятью переменными, но решение систем из нескольких сот линейных уравнений, встречающихся в геодезии, занимало иногда много месяцев работы нескольких вычислителей. Только с появлением ЭВМ решение больших линейных систем стало вполне доступным.

Теперь можно остановиться на сути метода Гаусса (методе последовательного исключения неизвестных для нахождения решений системы линейных алгебраических уравнений или приведение системы к треугольному виду - решения систем линейных уравнений). Методы подстановки и алгебраического сложения являются основными, которые рассматриваются на уроках математики.

П



ример. Дана система

2х - 4у + 4z = 10

-3x + 8y - 10 z = - 25 (1)

4x - 3y +z = 1

Преобразуем её в равносильную систему так, чтобы в первом уравнении переменная х стояла с коэффициентом единица, а в другие уравнения не входила вовсе. Для этого разделим почленно первое уравнение системы (1) на коэффициент при х, т. е. на 2. Получим первое уравнение новой системы:

x - 2y + 2z = 5.

Прибавляя почленно это уравнение, умноженное на 3, ко второму уравнению исходной системы и, умноженное на - 4, к третьему уравнению исходной системы, получим равносильную исходной систему, в которой переменная х будет исключена из второго и третьего уравнений:



x - 2y + 2z = 5

2y - 4z =-10 (2)

5y - 7z = -19.

Второе и третье уравнения системы (2) содержат только переменные у и z. Деля почленно второе уравнение на 2, получим уравнение

y - 2z = -5

с коэффициентом единица при переменной у. Прибавляя почленно это уравнение, умноженное на - 5, к третьему уравнению системы (2), получим:

3z = 6.

В результате мы получили систему:



x - 2y +2z = 5

y - 2z = -5 (3)

3z = 6



Разделив последнее уравнение на 3, приходим, наконец, к системе:

x - 2y +2z = 5

y - 2z = -5 (4)

z = 2,

в которой коэффициенты на диагонали равны единице, а коэффициенты влево от диагонали равны нулю (их мы не пишем). Такая система легко решается:

z =2, y = - 5 + 2z = - 1, x = 5 + 2y - 2z = -1.

Ответ: (- 1; - 1; 2)

З





адания. Решите системы уравнений.

x +y +z = -2 x + 2y -z = 7

a) x - y + 2z = -7 б) 2x - y + z = 2

2x + 3y - z = 1 3x - 5y + 2z = -7





x - y - z = 5 x - 3y + z = 7

в) 2x + y +3z = 3 г) 3x + y - 2z = 3





x - 4y - 6z = 7 x + 7y - 4z = 0

3х - 2у + 5z = 7 2х - 5у + z = -2

д) 7х + 4у - 8z = 3 е) 4х + 3у - 6z = 1

5х - 3у - 4z = -12 2х + 21y -15z = 8

Можно предложить учащимся практическую исследовательскую работу на разработку алгоритма решения систем из четырёх, пяти и более линейных уравнений, т. е. N уравнений, а затем программы на языке программирования QBASIC и реализации на ЭВМ. Если работа окажется трудноватой для учащихся, то учитель предлагает алгоритм решения и демонстрирует программу на ЭВМ.

В этом случае учителю рекомендуется разработать схему алгоритма.

Ниже приводится возможный вариант текста программы. Учитель должен сам решить, в какой мере он будет его анализировать. Можно ограничиться демонстрацией решения конкретной системы из трех или четырех уравнений. Можно подробно рассмотреть каждую строку программы и главным считать технику подготовки таких программ.

CLS

REM РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

INPUT "N = "; N

DIM A ( N, N), B ( N), X ( N)

FOR I =1 TO N

FOR J =1 TO N

PRINT"A ("; I; "," ; J;") =";

INPUT A ( I, J)

NEXT J

PRINT "B(" ; I ") = "; : INPUT B( I): NEXT I

REM ИСКЛЮЧЕНИЕ НЕИЗВЕСТНЫХ

FOR K = 1 TO N - 1

FOR I = K + 1 TO N

M = A( I, K)/A( K, K)

FOR J= K +1 TO N

A( I, J) = A( I, J) - M*A( K, J)

NEXT J

B( I )= B( I ) - M* B( K )

NEXT I

NEXT K

REM ОБРАТНАЯ ПОДСТАНОВКА

X (N) = B (N) / A (N, N)

FOR I = N - 1 TO 1 STEP - 1

S = 0

FOR J = I + 1 TO N

S = S + A (I, J) *X (J)

NEXT J

X (I) =(B (I) - S) / A (I, I)

NEXT I

FOR I = 1 TO N

PRINT "X ("; I; ")="; X( I )

NEXT I

END



Для примера можно рассмотреть решение методом Гаусса с применением ПК ниже приводимые системы:

А) 2, 1x₁ + 3, 4x₂ = - 4, 522

3, 5x₁ - 2, 3 x ₂= 9, 751 Ответ: (6, 160396; - 5, 13495)



1. 2, 73x₁ - 6, 2x ₂ + 1, 7x₃= 29, 1

2, 56x₁ + 3, 2x ₂ - 2, 5x ₃= 3, 805

1, 79x₁ - 2, 59x₂ + 6, 54x₃ = 24, 049



Ответ: (5, 333815; - 1, 948555; 1, 445675)

1. 4x₁ - 2x₂ + 3x₃ - 4x₄ = 14

2x₁ + 3x₂ - 2x₃ - x₄ = -1

x ₁+ 4x₂ +2x₄ = - 1

2x₁ - x₂ + x₃ = 4 Ответ: (1; 0; 2; -1)



1. x₁ + 2x₂ - x₃ - 2x₄ = - 6

3x₁ - x₂ + 3x₃ + x₄ = 4

2x₁+ x₂ - 2x₃ = 2

2x₂ - x₃ + 3x₄= 3 Ответ: (1; -2; -1; 2)

Литература:

1. Учебное пособие "Алгебра и начала анализа 9 - 10" под редакцией А. Н. Колмогорова, Москва: "Просвещение", 1983 г., п. 73. Решение систем линейных уравнений, стр. 224 - 228.

2. Справочник по элементарной математике под редакцией М. Я. Выгодского, Москва "Наука", Главная редакция физико - математической литературы, 1978 г.

3. Математический энциклопедический словарь под редакцией Ю. В. Прохорова, Москва "Советская энциклопедия", 1988 г.

4. Научно - методические журналы "Информатика и образование", "Математика в школе".

18