Щербакова Алена Вячеславовна
Учитель математики
Ясиноватская общеобразовательная школа I-II ступеней №5 -дошкольное образовательное учреждение Администрации города Ясиноватая
Город Ясиноватая
Программа факультативного курса для 7 класса
«УДИВИТЕЛЬНАЯ ГЕОМЕТРИЯ»
Программа факультативного курса для 7 класса
«УДИВИТЕЛЬНАЯ ГЕОМЕТРИЯ»
Вычисления и геометрические построения невозможны без логических рассуждений. Значит, в геометрии невозможно обойтись без логики. Каждому школьнику надо упорно учиться правильно мыслить. Учиться логически рассуждать нужно много и постоянно во всех классах средней школы. Для учеников 7 класса в этом отношении будет очень полезен предлагаемый элективный курс по геометрии содержащий большое количество нестандартных задач, развивающих логическое мышление и дающий представление о геометрии как одной из составляющей окружающего нас мира.
Актуальность создания факультативного курса.
Современному обществу нужна личность с творческим, неординарным мышлением, широким кругозором, умеющим ставить и решать нестандартные и оригинальные задачи.
Факультатив, как одна из форм внеурочных занятий, открывает большиевозможности по расширению математического кругозора учащихся, обобщению и систематизации знаний учащихся по отдельным темам математической дисциплины, способствует развитию интереса к изучению предмета, развивает творческие способности детей, знакомит с вариантами новых нетрадиционных подходов решения математических заданий.
Основные цели проведения факультативных занятий:
-углубление и расширение знаний по математике;
-развитие математического кругозора, мышления, исследовательских
умений учащихся;
-привитие интереса учащимся к математике.
Обучающие задачи:
-учить добывать и грамотно обрабатывать информацию;
-учить грамотной математической речи, умению обобщать и делать выводы;
-достигать более высоких показателей в основной учебе.
Развивающие задачи:
-развивать мышление в ходе усвоения таких приемов мыслительной деятельности как умение анализировать, сравнивать, синтезировать, обобщать, выделять главное, доказывать, опровергать;
-развивать умение быстрого счёта, быстрой реакции;
-развивать навыки успешного самостоятельного решения проблемы.
Воспитательные задачи:
-воспитывать активность, самостоятельность, ответственность, культуру общения;
-формировать умения строить математические модели реальных явлений, анализировать построенные модели, исследовать явления по заданным моделям;
-воспитывать трудолюбие.
Учебно-тематическое планирование
| № п/п | Содержание | К-во часов | Дата |
| 1 | Вводное занятие. Что такое геометрия. История развития. (1 час) | 1 |
|
|
| Удивительные задачи на разрезание (6 часов) |
|
|
| 2 | Задачи на клетчатой бумаге. | 1 |
|
| 3 | Задачи на нахождение площадей фигур способом разрезания | 1 |
|
| 4 | Задачи на нахождение площадей фигур способом разрезания и смещения частей фигуры. | 1 |
|
| 5 | Задачи на разрезание и моделирование геометрических фигур. | 1 |
|
| 6 | Танграм. | 1 |
|
| 7 | Пентамино. | 1 |
|
|
| Решение задач повышенной трудности(11 ) |
|
|
| 8 | Решение олимпиадных задач. | 1 |
|
| 9 | Разбор заданий школьного тура математической олимпиады. | 1 |
|
| 10 | Задачи на доказательство | 1 |
|
| 11 | Методы доказательства теорем. Доказательство от противного. | 1 |
|
| 12 | Разбиение плоскости. | 1 |
|
| 13 | В одной фигуре разные многоугольники. | 1 |
|
| 14 | Превращение многоугольника в квадрат. | 1 |
|
| 15 | Превращение правильного шестиугольника в равносторонний треугольник. | 1 |
|
| 16 | Построения с помощью циркуля и линейки | 1 |
|
| 17 | Решение задач на местности | 1 |
|
| 18 | Замечательные кривые | 1 |
|
|
| Решение геометрических задач (16 часов) | 1 |
|
| 19 | «Измерительные инструменты всегда при тебе». | 1 |
|
| 20 | Не отрывая карандаша… | 1 |
|
| 21 | Построение с препятствиями и ограничениями | 1 |
|
| 22 | Задачи со спичками. | 1 |
|
| 23 | Задачи по готовым рисункам. | 1 |
|
| 24 | Разбор заданий городского тура математической олимпиады. | 1 |
|
| 25 | Разбор заданий городского тура математической олимпиады. | 1 |
|
| 26 | Основные геометрические понятия. | 1 |
|
| 27 | Виды углов, построение углов. | 1 |
|
| 28 | Построение углов заданной величины. Деление угла в заданном соотношении. | 1 |
|
| 29 | Упражнения с листом бумаги. | 1 |
|
| 30 | Решение задач на местности | 1 |
|
| 31 | Параллельные и перпендикулярные прямые. | 1 |
|
| 32 | Задачи на построение. | 1 |
|
| 33 | Практические задания. | 1 |
|
| 34 | Итоговое занятие. Игра «Геометрический поединок». | 1 |
|
Ожидаемый результат
В результате изучения курса учащиеся:
Обобщат и систематизируют знания по отдельным темам геометрии.
Познакомятся с новыми методами решения задач.
Научатся грамотно отвечать на вопросы к задачам, выбирать и записывать полученный ответ, оформлять решение, в результате полученного опыта не будут испытывать чувство страха при решении задач различного уровня.
Овладеют навыками решения задач на построение с помощью циркуля и линейки.
Занятие 6. Танграм
Цель: познакомить учащихся с китайской головоломкой «Танграм». Попрактиковаться в геометрическом исследовании, конструировании. Развивать комбинаторные навыки.
Говоря о задачах на разрезание, нельзя не упомянуть о древней китайской головоломке «Танграм», возникшей 4 тыс. лет назад. В Китае ее называют «читао ту», то есть «умственная головоломка из семи частей» и о современных головоломках. «Танграм» из четырех частей тоже очень увлекательная. 
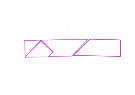

Методические рекомендации. Для проведения этого урока желательно иметь раздаточный материал: головоломку (которую могут изготовить сами школьники), рисунки фигур, которые нужно будет сложить. Разрезав квадрат так, как показано на рисунке, и соблюдая два правила:
1) при складывании фигурок использовать все части-«танов»;
2) «таны» нельзя накладывать друг на друга (они могут только касаться друг друга) можно сложить немало занимательных фигурок.
1. Изготовьте головоломку сами: переведите на плотную бумагу квадрат, разделенный на семь частей, и разрежьте его.
2. Используя все семь частей головоломки, составьте фигурки, изображенные на рис.

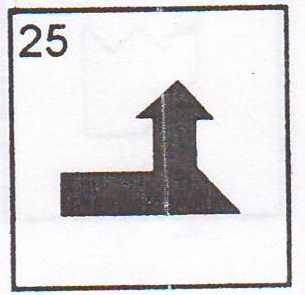
Рис. 2
Методические рекомендации. Детям можно раздать рисунки фигур (рис. 2) в натуральную величину. Поэтому школьник может решать задачу, накладывая части головоломок на рисунок фигуры, таким образом подбирая нужные части, что упрощает задачу.
3. Попробуйте придумать свою фигурку, используя все семь частей танграма.
4. В танграме среди его семи частей уже есть треугольники разных размеров. Но из его частей можно и еще сложить различные треугольники. Сложите треугольник, используя четыре части танграма:
а) один большой треугольник, два маленьких треугольника и квадрат;
б) один большой треугольник, два маленьких треугольника и параллелограмм;
в) один большой треугольник, один средний треугольник и два маленьких
треугольника.
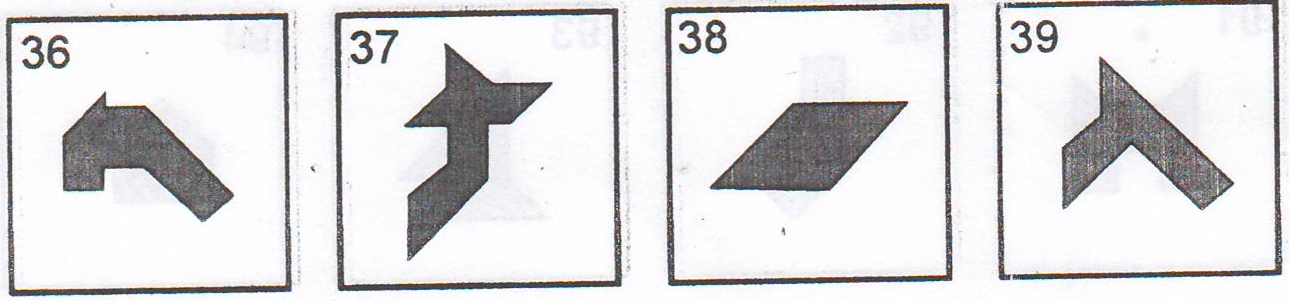

Чтобы сложить фигурку, нужно быть внимательным и проявить и настойчивость, аккуратность и терпение. Предлагаемые фигуры-задачи можно объединить по темам и сюжетам. Этого количества задач достаточно, чтобы сформировать у учащихся устойчивые навыки решения задач на разбиение и складывание.
Список используемой литературы:
Перельман Я.И. Занимательная арифметика. Триада-Литера Москва 2000 год.
Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия: Учебное пособие для учащихся V –VI классов. М.МИРОС,1995 год.
Геометрия ,7-9: учеб. Для общеобразоват. Учреждений/ [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]- М.: Просвещение, 2016.
Ткачева М.В. Домашняя математика: Кн. Для учащихся 7 кл. сред. шк.- М.: Просвещение, 1993.
Фарков А.В. Математические кружки в школе 5-8 класс. Москва. Айрис-пресс 2007 год.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Программа факультативного курса для 7 класса «УДИВИТЕЛЬНАЯ ГЕОМЕТРИЯ» (1.4 MB)
Программа факультативного курса для 7 класса «УДИВИТЕЛЬНАЯ ГЕОМЕТРИЯ» (1.4 MB)
 0
0 2608
2608 267
267 Нравится
0
Нравится
0




