Ханты-Мансийский автономный округ-Югра
Администрация города Мегиона
МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ №5 «ГИМНАЗИЯ» Научно-практическая конференция «Шаг в будущее-2014»
Направление работы:
«Математика и информационные технологии»
Тема: Новый способ нахождения наименьшего общего кратного чисел.
Автор: Смолянинов Юрий Юрьевич
ученик 7 А класса
Руководитель:
Савинкина Ирина Владимировна.
учитель математики
Мегион 2014г.
Аннотация
Цель работы: исследовать экспериментальным путём и статистически достоверно установить, что новый способ облегчает и ускоряет нахождение наименьшего общего кратного ( далееНОК чисел), используя методы математической статистики. Представить буклет с описанием нового способа в качестве приложения-вкладыша к учебнику математики 6 класса.
Методы и приёмы:
Экспериментальная проверка нового способа: выполнение ряда математических расчётов, направленных на получение данных, подтверждающих справедливость нового способа нахождения НОК для определённой группы чисел.
Экспериментальная проверка нового способа нахождения НОК чисел, работая в двух группах, одна из которых находит НОК традиционным ранее изученным способом (контрольная группа), а другая – используя новый способ (экспериментальная группа).
Статистическая обработка результатов с последующим построением соответствующих диаграмм.
Анализ статистически обработанных результатов, формулировка выводов, подтверждающих или опровергающих выдвинутую ранее гипотезу.
Выводы:
Новый способ значительно упрощает нахождения НОК чисел, экономит время, давая тем самым возможность увеличить объём выполненных на уроке заданий.
Статистически достоверно установлено, что шестиклассники, участвующие в эксперименте, отдают предпочтение новому способу, что подтверждает его актуальность практическую ценность.
План исследований
Актуальность: При сложении и вычитании обыкновенных дробей необходимо найти наименьший общий знаменатель (НОЗ). С 6 класса мы умеем это делать и знаем, что НОЗ – это не что иное, как наименьшее общее кратное (НОК) знаменателей. В ходе решений примеров и задач мы складывали или вычитали дроби, находя НОК знаменателей, и заметили, что для некоторых знаменателей НОК можно находить гораздо проще и быстрее, нежели традиционное разложение на простые множители.
Проблема: Определились два вопроса: во-первых - можно ли предложить для школьной программы математики 6 класса новый, более рациональный способ нахождения НОК чисел, упростив тем самым сложение и вычитание обыкновенных дробей с разными знаменателями; во-вторых – будет ли это нововведение полезным и нужным.
Гипотеза: На основании собственных вычислений НОК чисел новым способом была выдвинута следующая гипотеза:применение этого способа облегчает и ускоряет нахождение НОК чисел, а значит, он будет востребован при сложении и вычитании обыкновенных дробей с разными знаменателями.
Объект – Нахождение НОК чисел.
Предмет – новый способ нахождения НОК чисел.
Цель работы: На основании существующей проблемы и выдвинутой нами гипотезы была сформулирована следующая цель работы: исследовать экспериментальным путём и статистически достоверно установить эффективность и рациональность нового способа нахождения НОК чисел с использованием методов математической статистики.
Методы исследования: 1. Экспериментальный метод, состоящий из двух частей:: экспериментальной проверки нового способа нахождения НОК самостоятельно (индивидуально) путём выполнения расчётных математических задач по данной теме с последующим теоретическим анализом, и экспериментальной проверки нового способа в группах экспериментальной (по новому способу) и контрольной (по традиционному способу) и последующего сравнения результатов работы групп.
Метод социологического исследования - анкетирование участников эксперимента для объективной оценки эффективности нового способа нахождения НОК.
Статистическая обработка, полученных из анкеты, данных с последующим построением соответствующих диаграмм.
Анализ и обсуждение статистики обработанных результатов, формулировка выводов, подтверждающих или опровергающих выдвинутую ранее гипотезу.
Сравнительный метод исследования : изучение литературы и источников в интернете.
Библиография работы:
А.П.Савин. Энциклопедический словарь юного математика. М.: «Педагогика-Пресс» 1999г.
Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурд. Математика 6. М.:2009г.
Научная статья
Состояние изучаемой проблемы. Выбор объектов и методов исследования
Родоначальником наименьшего общего кратного был Евклид (3 в. до н.э.) В своей книге «Начала» он впервые вводит это понятие.
Для того, чтобы находить общий знаменатель при сложении и вычитании дробей с разными знаменателями необходимо уметь рассчитывать наименьшее общее кратное (НОК).
Кратное числу a - это число, которое само делится на число a без остатка.
Например: Числа кратные 8 (то есть, это числа, делящиеся на 8 без остатка):
8, 16, 24, 32 ...
Кратные 9: 9, 18, 27, 36, 45 ... Чисел, кратных числу a бесконечно много, в отличии от делителей этого же числа. Делителей - конечное множество.
Кратные и делители числа.
Общим кратным натуральных чисел называется число, которое делится на эти числа нацело.
Наименьшим общим кратным (НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел.
Как найти НОК
НОК можно найти и записать двумя способами.
Первый способ нахождения НОК
Данный способ обычно применяется для небольших чисел.
Выписываем в строчку кратные для каждого из чисел, пока не найдётся одинаковое кратное для обоих чисел.
Кратное числа a обозначим большой буквой «К».
К (a) = {...,...}
Пример. Найти НОК 6 и 8.
К (6) = {6, 12, 18, 24, 30, ...}
К (8) = {8, 16, 24, 32, ...}НОК (6, 8) = 24
Второй способ нахождения НОК
Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.
Разложить данные числа на простые множители. Подробнее правила разложения на простые множители вы можете прочитать в теме как найти наибольший общий делитель (НОД).разложение чисел на простые множители
Выписать в строчку множители, входящие в разложение самого большого из чисел, а под ним - разложение остальных чисел.
Количество одинаковых множителей в разложениях чисел может быть разное.
60 = 2 • 2 • 3 • 5
24 = 2 • 2 • 2 • 3
Подчеркнуть в разложении меньшего числа (меньших чисел) множители, которые не вошли в разложение бóльшего числа (в нашем примере это 2) и добавить эти множители в разложение бóльшего числа.
НОК (24, 60) = 2 • 2 • 3 • 5 • 2
Полученное произведение записать в ответ.
Ответ: НОК (24, 60) = 120
Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом.
Найдём НОК (12, 16, 24).
пример нахождения наименьшего общего кратного (НОК) 24 = 2 • 2 • 2 • 3
16 = 2 • 2 • 2 • 2
12 = 2 • 2 • 3
Как видим из разложения чисел, все множители 12 вошли в разложение 24 (самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из разложения числа 16.
НОК (12, 16, 24) = 2 • 2 • 2 • 3 • 2 = 48
Ответ: НОК (12, 16, 24) = 48
Удобнее оформлять нахождение НОК чисел так, как нам показывает учитель.
Например:
Разложив числа 441 и 700 на простые множители, найдите наименьшее общее кратное этих чисел.
Решение.
Разложим числа 441 и 700 на простые множители:
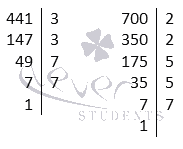
Получаем 441=3·3·7·7 и 700=2·2·5·5·7.
Теперь составим произведение из всех множителей, участвующих в разложениях данных чисел: 2·2·3·3·5·5·7·7·7. Исключим из этого произведения все множители, одновременно присутствующие в обоих разложениях (такой множитель только один – это число 7): 2·2·3·3·5·5·7·7. Таким образом, НОК(441, 700)=2·2·3·3·5·5·7·7=44 100.
Ответ:
НОК(441, 700)= 44 100.
Правило нахождения НОК с использованием разложения чисел на простые множители можно сформулировать немного иначе.
Если ко множителям из разложения числа a добавить недостающие множители из разложения числа b, то значение полученного произведения будет равно наименьшему общему кратному чисел a и b.
Особые случаи нахождения НОК
Если одно из чисел делится нацело на другие, то наименьшее общее кратное этих чисел равно этому числу.
Например, НОК (60, 15) = 60
Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее кратное равно произведению этих чисел.
Пример.
НОК (8, 9) = 72 [2], [3].
Как видим, существуют частные случаи, позволяющие отойти от общего способа. Этот факт сыграл свою роль, расширив поле деятельности при решении нашей проблемы. Желание найти более рациональный способ нахождения НОК чисел не покидало меня в течение нескольких дней. И вот однажды вечером, во сне пришла идея, как можно осуществить желаемое – находить НОК быстро и просто. Проснувшись среди ночи, я записал числа, которые увидел во сне, ещё не понимая до конца, что с ними можно сделать. Понадобилось ещё два дня и две ночи, чтобы сформулировать способ и определить – для каких чисел он будет применим.
Осталось этот способ «выпустить в мир».
Это и является целью моего проекта.
2.Экспериментальная часть
Объект исследования - наименьшее общее кратное чисел. Предмет – новый способ нахождения НОК чисел.
Эксперимент 1
Цель: Установить, что новый способ рациональный, прост в использовании.
Убедимся, что новый способ справедлив для разных пар чисел: двузначных, однозначных, трёх-, четырёхзначных, и т.д.
Мы рассмотрим сейчас нахождение НОК двузначного и однозначного чисел.
Найдём НОК (70 и 6). По традиционному способу, разложив эти числа на простые множители мы получаем следующее: 70 = 2*5*7 и 6 = 3*2 НОК (70 и 6) = 2*5*7*3= 210
А новым способом: НОК (70 и 6) = (70*6) : 2 = 210
Как видим, результат тот же. Но гораздо быстрее и легче это сделать новым способом, с этим нельзя не согласиться.
Точно так же можно показать, что новый способ справедлив и для других пар чисел: (30 и 4) ; (50 и 6) ; (8 и 90) …
Но, к сожалению, у нового способа есть один минус: он применим не ко всем числам.
Для того, чтоб воспользоваться новым способом нужно помнить условия: Одно из чисел – однозначное и чётное, т.е вида (2n), а другое – двузначное, нечётное в разряде десятков и оканчивается на 0.
Т.е. вида (2к -1)*10, то НОК равен половине произведения этих чисел.
((2n) * (2к-1)*10) / 2.
Обратите внимание: Я сформулировал сейчас условия для пары чисел – двузначное и однозначное.
Вывод: Новый способ позволяет более рационально находить НОК некоторых чисел.
Эксперимент 2.
Цель: Доказать, что по новому способу нахождение НОК чисел можно выполнить намного быстрее, чем по традиционному способу.
Чтобы ответить на второй вопрос проблемы мы провели эксперимент, в котором участвовало 23 человека
1 группа экспериментальная – 12 человек
2 группа контрольная – 11 человек
(список см. приложение 1)
Одни и те же числа мы предложили обеим группам.
Контрольная группа находила НОК обычным способом, экспериментальная - новым. Числа мы подобрали удовлетворяющие нашим условиям :
Найти НОК (70 и 6)
НОК (30 и 4)
НОК (8 и 10)
Чтобы закончить задание первому человеку из экспериментальной группы понадобилась 1 минута, а последнему 2 минуты (от начала эксперимента).
В контрольной группе первому человеку понадобилось 4 минуты, а последнему 9 минут.
Вывод: новый способ облегчает, а следовательно и ускоряет нахождение НОК.
3. Социологическое исследование и статистическая обработка данных, полученных из анкеты
Цель: выяснить - насколько новый способ будет востребован среди учащихся.
Я провел анкетирование, в котором участвовали 2 группы:
1)вопрос: Какой способ нравится больше?
Экспериментальный (т.е - мой) - 86,957% (20 человек)
Традиционный - 13,043% (3 человека)
вопрос: Почему?
Ответы: Легче, удобней, быстрей
Удобно- 21,7 % (5чел.)
Легко - 65,2% (15 чел.)
Быстро - 65,2% (15 чел.)
Был назван только один минус: данный способ применим не ко всем парам чисел.
На этот минус указали 22 человека из 23 - 95,7%.
1 человек вообще минусов не увидел.
И затем был задан следующий вопрос:
3)Будете ли использовать новый способ в их вычислениях?
Да - 65,2% (15чел)
Иногда - 34,8% (8чел)
Нет - 0% (0чел)
(Диаграммы см. приложение 2).
Вывод: Данный способ будет востребован обучающимися при нахождении НОК чисел, а значит и для приведения дробей к НОЗ.
Единственный минус моего способа – он применим не для всех чисел.
Я сформулировал и показал, что НОК чисел равен половине их произведения, используя пару: двузначное и однозначное число. Но он справедлив и для таких чисел, как например :
(98 и 990)
(96 и 970)
(112 и 1110)
(244 и 2450)
И Т.Д.
Если быть более точными, то для ВСЕХ чисел, у которых общий делитель только один = 2!
4. Доказательство уникальности нового способа.
Цель: выяснить – существовал ли ранее сформулированный нами способ нахождения НОК чисел.
Для этого я изучил ряд источников и выяснил, что подобный способ уже был сформулирован ранее, и он основан на связи наименьшего общего кратного с наибольшим общим делителем (далее НОД).
Вычисление наименьшего общего кратного (НОК) через НОД
Один из способов нахождения наименьшего общего кратного основан на связи между НОК и НОД. Существующая связь междуНОК и НОД позволяет вычислять наименьшее общее кратное двух целых положительных чисел через известный наибольший общий делитель. Соответствующая формула имеет вид
НОК(a, b)=a•b:НОД(a, b).
Рассмотрим примеры нахождения НОК по приведенной формуле.
Пример.
Найдите наименьшее общее кратное двух чисел (126 и 70).
Решение.
В этом примере a=126, b=70. Воспользуемся связью НОК с НОД, выражающуюся формулой НОК(a, b)=a•b:НОД(a, b).
То есть, сначала нам предстоит найти наибольший общий делитель чисел 70 и 126, после чего мы сможем вычислить НОК этих чисел по записанной формуле.
Найдем НОД(126, 70), используя алгоритм Евклида: 126=70•1+56, 70=56•1+14,56=14•4, следовательно, НОД(126, 70)=14.
Теперь находим требуемое наименьшее общее кратное:
НОК(126, 70)=126•70:НОД(126, 70)=126•70:14=630.
Ответ:
НОК(126, 70)=630.Пример.
Чему равно НОК(68, 34)?
Решение.
Так как 68 делится нацело на 34, то НОД(68, 34)=34.
Теперь вычисляем наименьшее общее кратное:
НОК(68, 34)=68•34:НОД(68, 34)=68•34:34=68.
Ответ:
НОК(68, 34)=68.
Заметим, что предыдущий пример подходит под следующее правило нахождения НОК для целых положительных чисел a и b: если число a делится на b, то наименьшее общее кратное этих чисел равно a. [1]
Вывод:
Получается, что я самостоятельно вывел, сформулировал и проверил способ нахождения НОК, который в школьной программе не применяется, но существует.
Только у меня более частный случай: он сформулировал способ для чисел с одним общим делителем - 2. А в представленный выше способ применим для всех чисел, и нужно найти их наибольший общий делитель.
Но, как бы там ни было, новый способ нахождения НОК свой я нашёл сам. Напомним, какая была первоначальная формулировка этого способа у меня:
Если одно из чисел – однозначное и чётное, т.е. вида (2n), а другое – двузначное нечётное в разряде десятков и оканчивается на 0.
т.е. вида (2к -1)*10, то НОК равен половине произведения этих чисел.
НОК = ((2n) * (2к-1)*10) / 2.
Именно эту формулировку способа я представляю в буклете-вкладыше, предлагая его в качестве приложения к учебнику Математика 6.
Социологическое исследование и статистическая обработка данных, полученных из итоговой контрольной работы
Цель: Убедиться по результатам итоговой контрольной работы в актуальности и эффективности моего способа.
В итоговую контрольную работу без предупреждения было включено одно задание, для которого было возможно применение нового способа.
После проверки и обработки результатов итоговой работы получили:
Из 81 обучающихся 38 решили использовать новый способ для нахождения НОК чисел (47%).
Из них – 36 обучающихся выполнили задание правильно, получив верный результат (95%)
Получили неверный результат – 2 обучающихся (5%). Причина в вычислениях, что не связано с применением моего способа.
Оставшиеся 43 человека не применяли новый способ. Из них – 22 обучающихся выполнили задание правильно, получив верный ответ (52 %) (Диаграммы см. в приложении 3)
Вывод:
52% против 95% - наглядный результат! Новый способ нахождения НОК чисел даёт отличные результаты! С применением моего способа можно упростить и ускорить выполнение соответствующих заданий, а так же повысить качество выполнения контрольных работ.
Вывод общий:
Новый способ нахождения НОК чисел подтвердил свою актуальность, востребованность и рациональность.
Достоинства нового способа: - лёгкость
- быстрота
Новый способ доступен даже ученику с низким уровнем математической грамотности.
Новый способ вполне может применяться и для нахождения общего знаменателя при сложении и вычитании обыкновенных дробей с разными знаменателями.
Предлагаю включить этот способ нахождения НОК чисел в учебное пособие в учебнике математики 6 класса как один из оптимальных способов нахождения общего знаменателя обыкновенных дробей.
Интернет-ресурсы:
http://www.cleverstudents.ru/divisibility/nok_finding.html - cleverstudents.ru - математика доступна каждому!
http://math-prosto.ru/?page=pages/find_nod_and_nok/find_nok.php - Школьная математика.
http://elenanikolaeva.ru/spravochnik-shkolnika/pravilo-naxozhdeniya-nok-neskolkix-chisel.html - Сайт репетитора по математике Елены Николаевой для школьников и их родителей.
Самооценка
Не только Менделееву снились его научные труды!
Работа над способом интересна не только потому, что упрощает нахождение НОК, но и тем, что в ходе работы выяснился факт, позволяющий расширить границы применения этого способа.
Всем, кто участвовал в эксперименте, мой способ очень понравился. Особенно экспериментальной группе, когда они быстро и легко, благодаря новому способу нахождения НОК, справились с поставленной задачей, гораздо быстрее контрольной группы. А затем его оценили и все те, кто был в контрольной группе, как только им о нём рассказали.
Перспективы.
Я определил, что нахождение НОК чисел вида (2450 и 244); (990 и 98); (14430 и 1442) и т.п., тоже можно сформулировать отдельным правилом. Это поле ещё не освоено, есть предмет для исследования. А значит, исследовательскую работу можно продолжить.
Кроме того, при работе с ресурсами я обнаружил, что существует алгоритм нахождение НОК отрицательных чисел, что мной ещё не изучено.
Впереди ещё много интересного!
Приложение 1
Контрольная группа Экспериментальная группа
1)Нестеров Никита 1) Зайцев Максим
2)Алиева Мадина 2) Бородынкина Валерия
3)Нагибин Данил 3)Липкин Данил
4)Швецов Евгений 4)Николаева Анастасия
5)Гноянко Яна 5)Зубаилова Айзанат
6)Симонова Маргарита 6)Стретович Семен
7)Тотолина Кристина 7)Сулейманов Тамерлан
8)Белоусова Анастасия 8)Львов Егор
9)Лысая Диана 9)Сабитов Марат
10)Александрова Екатерина 10)Ковальчук Илья
11)Огурцова Настя 11)Куприянчук Виктория
12)Сачан Виктория
Приложение 2


Приложение 3
![]()
![]()
![]()
![]()

 Получите свидетельство
Получите свидетельство Вход
Вход



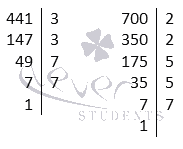











 Проектная работа по математике "Новый способ нахождения наименьшего общего кратного чисел" (0.39 MB)
Проектная работа по математике "Новый способ нахождения наименьшего общего кратного чисел" (0.39 MB)
 0
0 1596
1596 74
74 Нравится
0
Нравится
0


