Проектная деятельность при изучении величин в курсе математики в начальной школе как средство формирования познавательной активности учащихся
Учитель начальных классов : Якубова Юлия Валерьевна
СОДЕРЖАНИЕ
ВВЕДЕНИЕ……………………………….…….……………………….………..3
ГЛАВА 1. ТЕОРЕТИЧЕСКИЙ ОБЗОР СТРУКТУРЫ И ОСОБЕННОСТЕЙ ПРОЕКТНОЙ ДЕЯТЕЛЬНОСТИ ПРИ ИЗУЧЕНИИ ВЕЛИЧИН В МАТЕМАТИКЕ В КУРСЕ НАЧАЛЬНОЙ ШКОЛЫ……...……………………………………………………………...…....6
1.1. Понятие, структура и сущность проектной деятельности……………….6
1.2. Характеристика принципов, критериев и этапов проектной деятельности……………………………………………………………………16
1.3. Характеристика методики организации проектной деятельности в начальной школе …………………………..………………………………......23
1.4. Анализ особенностей изучения величин в математике как средстве формирования познавательной активности…………………….…………….39
Выводы……………………………………………………………....................44
ГЛАВА 2. ИССЛЕДОВАНИЕ ОСОБЕННОСТЕЙ ПРОЕКТНОЙ ДЕЯТЕЛЬНОСТИ ПРИ ИЗУЧЕНИИ ВЕЛИЧИН В КУРСЕ МАТЕМАТИКИ В НАЧАЛЬНОЙ ШКОЛЕ, КАК СРЕДСТВА ФОРМИРОВАНИЯ ПОЗНАВАТЕЛЬНОЙ АКТИВНОСТИ…….………45
2.1. Цели, задачи исследования……………………………………………….45
2.2. Методика и этапы программы исследования…………………………..48
2.3. Анализ результатов………………………………………………………..63
Выводы………………….………………………………………………………81
ЗАКЛЮЧЕНИЕ……………………………………………………………….83
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ……………………….85
ПРИЛОЖЕНИЕ……………………………………………………………….88
ВВЕДЕНИЕ
Актуальность работы обусловлена тем, что процессы глобализации, становление постиндустриального, информационного общества поставили перед школьным образованием новые задачи. Роль школы в решении этих задач определена в современных образовательных стандартах и примерных программах основного общего и среднего (полного) общего образования по всем учебным предметам.
Сегодня учитель призван не только сформировать у учеников системные знания, но и научить применять усвоенные знания и умения в практической деятельности и повседневной жизни, создать условия для всестороннего развития личности.[7]
Для успешного решения задач модернизации образования необходимы новые подходы к конструированию содержания школьных предметов, совершенствование технологий и методик обучения. Одним из вариантов комплексного решения задач современного школьного образования является проектная деятельность, позволяющие формировать у учащихся способность к осуществлению практической деятельности – способность определять цель деятельности и планировать пути ее достижения, анализировать и оценивать результаты.
Этот метод способствует формированию у учащихся следующих умений: составлять план работы по выполнению проекта, разбиваться на группы, распределять роли внутри группы, определять сроки выполнения проекта, определять необходимые для реализации проекта материалы, данные и выяснять места, откуда они будут браться, обобщать полученную информацию, представлять результат проделанной работы.[29]
В работах Н. Ю. Пахомовой, Е. С. Полат, И. Д. Чечель, И.К. Баталиной. М.А. Барсуковой, С. Шишова раскрыт педагогический потенциал проектной деятельности школьников; Г.В. Нарыковой, Е.А.Гилевой, Ю.С. Егоровым, Е.В. Клоковым Н.Мансуров охарактеризованы этапы учебного проекта, роль учителя на каждом из них; И.Д. Чечель, С. Лернер предложили различные подходы в оценивании проектной деятельности.
Наконец, Е.С. Полат, М.В. Игнатьевым, М.А. Барсуковой, Н.И. Заикиной, Е.А. Адаричевой рассмотрены особенности проектной деятельности на уроках математики.
Проблема, поставленная в данном исследовании, заключается в необходимости выявления условий формирования познавательной активности, необходимой для осуществления проектной деятельности младших школьников в обучении математике.
Объект исследования – процесс организации учебной проектной деятельности школьников начальных классов.
Предмет исследования – формирование познавательной активности в процессе организации проектной деятельности младших школьников при обучении курса математике.
Цель работы - изучить сущность и особенности проектной деятельности школьников начальных классов, которая способствует развитию активности, формирующейся в ходе работы над проектами.
Задачи:
- рассмотреть сущность и структуру проектной деятельности:
- охарактеризовать принципы, этапы и форму организации проектной деятельности;
- описать методику и программу организации проектной деятельности в начальной школе;
- проанализировать особенности изучения величин в математике в младшей школе как средства формирования познавательной активности;
- в практической части на конкретной примере провести исследования проектной деятельности при изучении величин в курсе математике в начальной школе как средства формирования познавательной активности.
Работа состоит из двух глав, введения, заключения и приложений. В ведение описывается актуальность, цель работы, предмет и объект исследования. Первая глава представляет собой теоретический и эмпирический обзор по теме работы.
Во второй главе проведено практическое исследование по данной теме. Заключение представляет собой выводы о проделанной работе. В приложении описывается программа исследования и результаты исследования (таблицы и диаграммы).
При выполнении данной работы использовались статьи, журналы, а также литература таких авторов, как Пахомова Н.Ю., Мансуров Н., Заикина Н.И., Бантова М.А., Волкова С.И. и т.д.
ГЛАВА 1. ТЕОРЕТИЧЕСКИЙ ОБЗОР СТРУКТУРЫ И ОСОБЕННОСТЕЙ ПРОЕКТНОЙ ДЕЯТЕЛЬНОСТИ ПРИ ИЗУЧЕНИИ ВЕЛИЧИН В МАТЕМАТИКЕ В КУРСЕ НАЧАЛЬНОЙ ШКОЛЫ
1.1. Понятие, структура и сущность проектной деятельности
В настоящее время в образовательную деятельность школ вводят новые педагогические технологии, используют активные методы обучения, в том числе и метод проектов. Это происходит потому, что обычная школа, в которой ученик выступает объектом обучения, теряет свою актуальность. На ее место приходит другая школа, в которой учащиеся могут проявить свои таланты и индивидуальность, научиться выбирать и принимать решения.
О.В Рыбина [31] считает, что перед такой школой стоят новые задачи. Педагог должен создать среду, которая бы мотивировала учащихся самостоятельно добывать, обрабатывать информацию, обмениваться ею, а также быстро и свободно ориентироваться в окружающем информационном пространстве.
Для учащихся должны быть созданы условия, которые способствуют их развитию по разным предметам, но в тоже время необходимо снизить нагрузку учащихся.
Для осуществления этих задач необходимо сделать учебный процесс более увлекательным и интересным, раскрыть значение получаемых в школе знаний и их практическое применение в жизни.
Т. Громова и О. Быкова [15] утверждают, что в соответствии с требованиями новой парадигмы образования главной задачей школы является подготовка образованной, творческой личности, способной к непрерывному развитию и самообразованию.
Это предполагает поиск новых форм и методов обучения, обновление содержания образования, в том числе использование наряду с традиционными, методов развивающего обучения и, в первую очередь, метода проектов.
Метод проектов имеет давнюю историю.
Над этим вопросом работали такие ученные, как Б.Валясэк, В.А. Кальней, Т.М. Матвеева, Е.А. Мищенко, С.Е. Шишов, И. Трухин , А.Н. Бренчугина-Романова, Е.С. Полат, В. Рохлов, Л.О. Филатова, И.А. Колесникова, М.П. Горчакова-Сибирская , В.А. Кальней, Т.М. Матвеева, Е.А. Мищенко, С.Е. Шишов, В. Рохлов, Г.В. Нарыкова, В.Н. Рязанова, Н.К. Солопова [32].
Со временем идея метода проектов изменилась, отмечает В. Рохлов. Из компонента свободного воспитания она становится важной частью вполне разработанной и структурированной системы образования.
Но суть ее остается прежней - стимулировать интерес учащихся к определенным проблемам, предполагающим владение определенной суммой знаний через проектную деятельность.
В современной педагогике метод проектов рассматривают как одну из личностно ориентированных технологий обучения, интегрирующую в себе проблемный подход, групповые методы, рефлексивные, презентативные, исследовательские, поисковые и прочие методики. Он используется не вместо систематического предметного обучения, а наряду с ним как компонент системы образования.
На сайте Интернет говориться, что формирование проектной деятельности учащихся необходимо для вооружения их универсальным умением решения различных проблем, в том числе и образовательных.
В современной педагогике проектная деятельность должна использоваться не вместо классно – урочной системы обучения, а наряду с ней, как компонент системы образования, как на уроке, так и во внеурочной деятельности. При этом педагогическая эффективность метода учебного проекта может быть представлена схемой:
Реализует деятельностный подход в обучении
Основан на принципе индивидуально сконцентрированного обучения
Построен на принципах проблемного обучения


Педагогические возможности проектного метода


Способствует развитию внутренней мотивации к учению
Способствует развитию конструктивного критического мышления школьников
Обеспечивает формирования основных компетенций учащихся, т.е. умений:
-проблематизации;
-целеполагания;
-планирования деятельности;
-самоанализа и рефлексии;
- сравнения, анализа, синтеза, прогнозирования;
-самостоятельного поиска, хранения и практического применения необходимой информации (в т.ч. с использованием электронных носителей);
-презентации хода самостоятельной деятельности
и её результатов;
-коммуникативности и толерантности.
Схема 1. Педагогическая эффективность метода проектов
Метод учебного проекта способствует развитию самостоятельности ученика, всех сфер его личности, обеспечивает субъектность ученика в образовательном процессе, следовательно, проектное обучение может рассматриваться как средство активизации познавательной деятельности учащихся, средство повышения качества образовательного процесса.
Таким образом, сегодня метод проектов понимается не только как один из способов организации взаимосвязанной деятельности учителя и учащихся («метод обучения»), но и как целостная «педагогическая технология», которая:
а) предполагает возможность диагностического целеполагания, планирования и проектирования процесса обучения, поэтапной диагностики, варьирования средств и методов с целью коррекции результатов;
б) включает в себя обоснованную систему приемов и форм деятельности учителя и учащихся на различных этапах реализации учебного проекта, сформулированные критерии оценки результатов этой деятельности;
в) применяется при изучении разных школьных предметов в образовательных учреждениях различного типа.
В настоящее время авторы дают различные определения проекту (см. Приложение 2).
Л. Иванова [20] дает следующее определение. Проект – это самостоятельная творческая работа учащегося, выполненная от идеи до ее воплощения в жизнь с помощью консультаций учителя.
В нашем исследовании за рабочее определение примем определение проекта, данное Л. Ивановой.
Процесс выполнения творческих проектов на каждом из этапов обучения предполагает не только комплексное использование учащимися изученного на каком-то определенном предмете, но и опору на знания и умения, полученные из других школьных дисциплин, а также свой личный опыт.
Это создает благоприятные условия для осуществления личностно-ориентированного подхода в обучении, формирования у школьников таких ценностных качеств, как самостоятельность, ответственность, критичность и требовательность к себе и другим, настойчивость в достижении поставленной цели, умение работать в команде.
Под проектной деятельностью будем понимать такую деятельность, в основе которой лежит активизация познавательной и практической составляющих, в результате которой школьник производит продукт, обладающий субъективной (иногда объективной) новизной. [14]
Проектное обучение – организация образовательного процесса, направленная на решение обучающимися учебных задач на основе самостоятельного сбора по данным признакам и интерпретации информации, обязательного обоснования и корректировки последующей продуктивной учебной деятельности, ее самооценки и презентации результата. Обучение при этом принимает большой личностный смысл, что заметно повышает мотивацию собственно учения.
Основной формой проектного обучения является метод проектов, которому в литературе даются различные определения.
Л.О.Филатова представляет определение В.В.Копыловой: «Метод проектов - целенаправленная, в целом самостоятельная деятельность учащихся, осуществляемая под гибким руководством учителя, направленная на решение исследовательской или социально значимой прагматической проблемы и на получение конкретного результата в виде материального и (или) идеального продукта». Примем его в качестве основного.
В методической литературе существует две точки зрения на то, что лежит в основе метода проектов.
В основе метода проектов лежит идея о направленности учебно-познавательной деятельности школьников на результат, который достигается благодаря решению той или иной практически или теоретически значимой для ученика проблемы.
Внешний результат можно будет увидеть, осмыслить, применить на практике. Внутренний результат - опыт деятельности - достояние учащегося, соединяющий знания и умения, компетенции и ценности.
Вторая, точка зрения представлена у Т. Громовой и О. Быковой, Г.В.Нарыковой, Л. Ивановой.
В основе метода проектов лежит развитие познавательных навыков учащихся, умений самостоятельно конструировать свои знания, развитие критического и творческого мышления, умение увидеть, сформулировать и решить проблему.
Говорится именно о решении какой-то проблемы, предусматривающей с одной стороны использование разнообразных приемов, с другой – интегрирование знаний и умений из различных областей науки, техники, творческих областей.
Результаты выполненных проектов должны быть «осязаемыми», т.е. если это теоретическая проблема, то ее конкретное решение, если практическая – конкретный результат, готовый к внедрению.
В своей работе Г.В. Нарыкова приводит точки зрения авторов В.В.Гузеева и Г.К.Селевко на основы проектного метода. В.В.Гузеев отмечает, что технология обучения на основе метода проектов представляет один из возможных способов проблемного обучения. По мнению автора, суть данной технологии заключается в следующем.
Учитель ставит школьникам учебную задачу, представляя тем самым исходные данные и очерчивая планируемые результаты. Все остальное учащиеся выполняют самостоятельно: намечают промежуточные задачи, ищут пути их решения, действуют, сравнивают полученное с требуемым результатом, корректируют деятельность.
Такого же мнения придерживается и Н.Ю. Пахомова. Г.К. Селевко [25] рассматривает метод проектов как системообразующий компонент при описании и характеристике различных технологий.
Он этот метод представляет так:
вариант технологии проблемного обучения;
комплексный обучающий метод, позволяющий индивидуализировать учебный процесс, дающий возможность ученику проявить самостоятельность в планировании, организации и контроле своей деятельности;
способ группового обучения;
альтернативная технология свободного труда;
технология развивающего обучения с направленностью на развитие творческих качеств личности;
технология саморазвивающего обучения.
Таким образом, Г.К. Селевко шире определяет сущность метода проектов в условиях современного образования, нежели В.В. Гузеев.
Большинство авторов отмечают, что использование метода проектов способствует развитию самостоятельности у школьников, учит объективно оценивать свою деятельность, развивает коммуникативные навыки, в процессе работы над проектом у школьников развиваются организационные и рефлексивные способности.
Н.В. Матяш и В.А. Кальней, Т.М. Матвеева, Е.А. Мищенко, С.Е. Шишов [23] полагают, что в процессе проектная деятельность способствует развитию следующих способностей у школьников:
коммуникативных, которые развиваются в процессе обсуждения творческих заданий, организации консультации с учителем, защиты в общении со сверстниками самых смелых идей;
личностных, а именно самобытности и гибкости мышления, фантазии, любознательности, здоровых творческих амбиций;
социальных: способности к коллективной деятельности, готовности соблюдать самодисциплину, терпимости к мнению других;
литературно-лингвистических: описание идеи, разработка рекламного прайс-листа, импровизация в процессе защиты;
математических: расчет затрат, соотнесение формы и объема, пространства и времени;
художественно-соматических: разработка изделий, их дизайн;
манипулятивных: умение пользоваться инструментами и приспособлениями, координация движений;
технологических: наглядно-образная память, абстрактно-логическое мышление.
С. Герасимова [11] говорит, что наряду с вышеперечисленными способностями у учащихся развиваются операционные структуры умственной деятельности (способность к анализу, синтезу, конкретизации и т.д.).
Е.А. Гилева, Ю.С. Егоров [13] отмечают, что метод проектов способствует формированию у учащихся чувства ответственности за принятые ими решения, способность работать в группе (при коллективном проекте), а также обучение анализу своей деятельности и ее результатов, при этом у школьников формируется умение описать процесс своей деятельности, способность применять на практике полученные знания по базовым предметам.
В то же время у учеников развиваются организационные и рефлексивные способности.
Таким образом, метод проектов позволяет формировать технологическую культуру и элементы проектного мышления и проектной культуры учащихся.
Можно заметить, что метод проектов способствует развитию различных способностей у учащихся, сбережению их здоровья.
Но в методической и педагогической литературе имеется материал, в котором описаны причины, мешающие успешному внедрению метода проектов в педагогическую практику школы, а также проблемы, возникающие при внедрении данного метода.
Этот вопрос освещают в своих работах Т.Н. Гуленко [18], И.С. Сергеев, С. Шишов, Н.В. Матяш [29], В. Рохлов.
В.Стрельцов отмечает, что метод проектов нужно применять на различных этапах становления личности ученика, начиная с младшего школьного возраста.
По его мнению, проектную деятельность следует организовывать для младших учащихся во внеурочное время. Это тоже не всегда возможно.
По мнению О.В. Швецова, младший школьный возраст является начальным этапом вхождения в проектную деятельность, закладывающим фундамент дальнейшего овладения ею. Проектная деятельность в младшей школе должна осуществляется поэтапно.
На каждом этапе следует использовать определенные методы обучения.
Автор говорит о сущности:
метода демонстрации образцов ранее выполненных проектов,
метода информационной поддержки,
метода мозговой атаки,
метода мини-маркетингового исследования,
метода мини-маркетингового сравнения,
метода информационной поддержки,
метода дизайна,
метода морфологического анализа,
метода фокальных объектов, алгоритмического метода исследования проектируемого объекта,
метода упражнений и других.
Несмотря на перечисленные трудности внедрения метода проектов, некоторые учителя применяют его в своей образовательной практике.
Для привлечения учителей к овладению методом проектов существует система проведения конкурсов проектов.
В.А.Кальней, Т.М.Матвеева, Е.А.Мищенко, С.Е.Шишов [23] отмечают, то, что метод проектов имеет особую значимость в учебно-воспитательном процессе технологической подготовки учащихся.
Он позволяет школьникам в системе овладеть организацией практической деятельности по всей проектно-технологической цепочке - от идеи до ее реализации в модели, изделии (продукте труда).
Очевидно, что метод проектов отличается от традиционных методов обучения, Б. Валясэк представляет точку зрения Мирослава С. Шиманськи, который выделил категории, по которым можно отличить метод проектов от других методов обучения:
прогрессивная роль учителя, который руководит деятельностью учеников, оказывает им помощь и вмешивается лишь только в том случае, если в этом есть необходимость;
субъективность учащегося. В проектах, над которыми он работает, важен не его результат (конечный продукт), а сам процесс работы над проектом, когда ученики осваивают новые знания, умения, учатся самостоятельности, ответственности, сотрудничеству;
сведение на нет границы между школьной и внешкольной жизнью. Проекты, которые учащиеся решают в социальной среде, учат целостному видению мира, поскольку ученики в процессе выполнения проекта должны самостоятельно овладеть содержанием различных областей знаний с помощью умственной и физической работы, а также с помощью эмоций;
отсутствие традиционной оценки. Само участие в осуществлении проекта свидетельствует о прогрессе учащегося, и оценка становится лишней. Мы считаем, что метод проектов по ряду признаков превосходит традиционные методы обучения. Он позволяет показать школьникам не только теоретические аспекты изучаемого предмета, но и научить их применять свои знания на практике, в жизни.
1.2. Характеристика принципов, критериев и этапов проектной деятельности
Метод проектов в методической и педагогической литературе освещен достаточно полно, но возможность его реализации в процессе обучения математике затронута лишь некоторыми авторами.
Исходя из природы проектирования, следует осознавать факт отсутствия однозначных решений в педагогических проектах, т.е. содержательную и технологическую вариативность проектной деятельности. При внедрении метода проектов в образовательную практику следует учитывать некоторые принципы.
Е.С. Полат под принципами проектной деятельности подразумевает общие регулятивы, которые нормируют проектную деятельность. Он формулирует и раскрывает их следующим образом.
Принцип прогностичности обусловлен самой природой проектирования, ориентированного на будущее состояние объекта.
Особенно ярко он проявляется при использовании проектирования для создания инновационных образцов. В этом смысле проект может быть определен как пошаговое осуществление потребного будущего.
Принцип пошаговости.
Природа проектной деятельности предполагает постепенный переход от проектного замысла к формированию образа цели и образа действий. От него – к программе действий и ее реализации. Причем каждое последующее действие основывается на результатах предыдущего.
Принцип нормирования
требует обязательности прохождения всех этапов создания проекта в рамках регламентированных процедур, в первую очередь связанных с различными формами организации мыследеятельности.
Принцип обратной связи
напоминает о необходимости после осуществления каждой проектной процедуры получать информацию по ее результативности и соответствующим образом корректировать дейс
твия.
Принцип продуктивности
подчеркивает прагматичность проектной деятельности, обязательность ее ориентации на получение результата, имеющего прикладную значимость. Иными словами, на «продуктную оформленность» результатов процесса проектирования.
Принцип культурной аналогии
указывает на адекватность результатов проектирования определенным культурным образцам. Опасность получения проектного результата, лежащего вне культурного поля, снимается, если у участников проектной деятельности есть понимание того, что индивидуальное творчество ученика или педагога не является самодостаточным.
Чтобы быть включенным в культурный процесс, необходимо научиться понимать и чувствовать свое место в нем, формулировать собственный взгляд на достижения человечества на основе изучения культурно-исторических аналогов.
При этом получение научных знаний и знакомство с культурными ценностями важно осуществлять в сопоставлении с собственными суждениями и результатами познавательной деятельности.
Принцип саморазвития
касается как субъекта проектирования на уровне ветвящейся активности участников, так и порождения новых проектов в результате реализации поставленной цели.
Решение одних задач и проблем приводит к постановке новых задач и проблем, стимулирующих развитие новых форм проектирования.
Рассмотрим дидактические принципы, о которых говорит Л. Иванова [20].
Принцип детоцентризма.
В центре творческой деятельности находится ученик, который проявляет активность. В проектном обучении у него имеется возможности реализовать себя, ощутить успех, продемонстрировать другим свою компетентность.
Принцип кооперации.
В процессе работы над проектом организуется и осуществляется широкое взаимодействие учащихся с учителем и между собой в проектных группах; возможно привлечение консультантов из различных сфер деятельности.
Принцип опоры на субъектный опыт учащихся.
Каждый школьник, работая над проектом, имеет хорошие возможности применить уже имеющиеся у него собственный опыт и знания.
Принцип учёта индивидуальности учащихся.
В работе важно учитывать интересы учеников, темп работы, уровень обученности.
Принцип свободного выбора.
Ученики имеют право выбирать темы проекта, подтемы, партнёров, источники и способы получения информации, методы исследования, формы представления результатов. Возможность выбора способствует повышению ответственности учащихся, их мотивации и познавательной активности.
Принцип связи исследования с реальной жизнью.
Происходит соединение академических знаний и практических действий. Предполагается, что проектная работа в той или иной степени направлена на улучшение окружающего мира; проект имеет прагматическую направленность на результат.
Принцип трудной цели.
Этот принцип важно учитывать, поскольку легко достижимый результат не является для многих учащихся мобилизующим фактором. Этих же принципов придерживается и Е.В. Петухова .
Н.А. Беломестнова [6] также говорит о существовании определённых принципов проектной деятельности:
вариативности (использование индивидуальной, парной, групповой форм работы, выбор темы и различных форм представления результатов);
решения проблемы (проблема заставляет учащихся думать, а значит – учиться);
самостоятельности (уточнение формулировки задачи, выбор формы проекта, распределение заданий в группе, систематизация промежуточных материалов);
создания комфортной обстановки на уроке (отсутствие страха перед общением математике помогает лучше усваивать трудные темы программы);
учения с увлечением (усвоение материала идёт легче, если процесс учащимся нравится);
личностного фактора (проектная работа предоставляет ребятам возможность думать и говорить о себе, своей жизни, своих интересах, увлечениях);
адаптации заданий (нельзя предлагать ученику задание, с которым он не сможет справиться, при выборе задания следует учитывать возрастные особенности, учебные возможности, этап работы над проектом).
За основу примем принципы, предложенные Е.С. Полат.
Авторы Рязанова В.Н., Солопова Н.К. , Н.М. Чумичева , А.В. Хуторской, Е.С. Полат в своих исследованиях помимо принципов отмечают также требования к использованию метода проектов.
Е.С. Полат выделяет следующие требования:
Наличие значимой в исследовательском плане проблемы (задачи), требующей интегрированного знания, исследовательского поиска для ее решения;
Практическая, теоретическая, познавательная значимость предполагаемых результатов;
Самостоятельная (индивидуальная, парная, групповая) деятельность учащихся;
Структурирование содержательной части проекта (с указанием поэтапных результатов);
Использование исследовательских методов, предусматривающих определенную последовательность действий:
определение проблемы и вытекающих из нее задач исследования (использование в ходе совместного исследования метода «мозговой атаки», «круглого стола»);
выдвижение гипотез и их решение;
обсуждение методов исследования (статистических методов, экспериментальных, наблюдений и пр.);
обсуждение способов оформления конечных результатов (презентации, защиты, творческих отчетов, просмотров и т.д.);
сбор, систематизация и анализ полученных данных;
подведение итогов, оформление результатов, их презентация;
выводы, выдвижение новых проблем исследования.
За основу примем требования, которые выдвигает Е.С. Полат.
Авторы отмечают, что в процессе реализации проектной деятельности учет принципов и требований необходим и обязателен.
В литературе существуют различные классификации проектов.
В качестве основной примем классификацию, предложенную Е.С.Полат.
В реальной практике чаще всего встречаются смешанные типы проектов. Каждый тип проекта характеризуется тем или иным видом координации, сроками исполнения, этапностью, количеством участников.
Поэтому, разрабатывая проект, надо иметь в виду признаки и характерные особенности каждого из них.
В ходе осуществления проектной деятельности в исследованиях некоторых авторов выделены фазы проектной деятельности.
Например, С.Н. Поздняк выделяет такие фазы осуществления проектной деятельности, как проектировочная, технологическая, рефлексивная, Б. Валясэк [10] выделяет пять фаз, а Г.В. Степанова – 7
В методической литературе авторы наряду с фазами проектной деятельности выделяют этапы организации проектной деятельности. Рассмотрим их подробнее.
Предлагаются рассмотрению этапы организации проектной деятельности аналогичные тем, которых придерживаются Н. Мансуров, Т. Герасимова, В. Рохлов [19].
Рассмотрим их подробнее.
1. Планирование начинается с его коллективного обсуждения.
Это, прежде всего обмен мнениями и согласованиями интересов учащихся; выдвижение первичных идей на основе уже имеющихся знаний и разрешения спорных вопросов. Затем предложенные учащимися темы проектов выносится на обсуждение.
2. Аналитический этап.
Этот этап самостоятельного проведения исследования, получения и анализа информации.
На этом же этапе членам группы необходимо договориться о распределении работы и формах контроля работы над проектом. Каждый ученик может вести «индивидуальный журнал», в котором он будет записывать ход работы. Можно вести общий журнал для всех участников проекта.
Это поможет учителю (да и самому ученику) оценить индивидуальный вклад каждого в работу над проектом, а также облегчить контроль. Введение индивидуального журнала для ученика, на наш взгляд, зависит от конкретных ситуаций и не является обязательным.
3. Этап обобщения информации.
На этом этапе осуществляются структурирование полученной информации и интеграции полученных знаний, умений, навыков.
4. Этап представления полученных результатов работы над проектом (презентация).
На этом этапе учащиеся осмысливают полученные данные и способы достижения результата; обсуждают и готовят итоговое представление результатов работы над проектом (в школе, округе, городе и т.д.).
Учащиеся представляют не только полученные результаты и выводы, но и описывают приемы, при помощи которых была получена и проанализирована информация; демонстрирует приобретенные знания и умения; рассказывают о проблемах, с которыми пришлось столкнуться в работе над проектом.
Мы за основу примем этапы, предложенные Н. Мансуровым, Т. Герасимовой, В. Рохловым.
В методической литературе есть информация о применении метода проектов в общеобразовательной практике школы на уроках математики. Проанализируем литературу, содержащую данную информацию.
И.К. Баталина и М.В. Игнатьев [5] говорят, что наибольшие проблемы внедрения метода проектов возникают в преподавании математики. Дело в том, что современная «школьная» математика, на первый взгляд, представляет из себя свод жестких непреложных правил и методов, точное и аккуратное следование которым порождает у школьников иллюзию успеха.
Но самое интересное и самое трудное возникает тогда, когда ученик сталкивается со сложной нестандартной задачей, из условия которой не видно, какая именно комбинация стандартных приемов приведет к правильному решению.
И главным препятствием для поиска решения такой задачи является результат тяжелого учительского труда: набор шаблонов и стереотипов, неизбежно выработанный на уроках, а также страх совершить ошибку, парализующий фантазию и естественное стремление ребенка к творчеству.
М.А. Барсукова [4] утверждает, что использование метода проектов на уроках математики позволяет реализовать деятельностный подход в обучении учащихся, интегрировать знания и умения, полученные ими при изучении различных школьных дисциплин на разных этапах обучения.
Главная цель организации проектной деятельности — развитие у учащихся глубоких, устойчивых интересов к предмету математики, на основе широкой познавательной активности и любознательности.
В достижении этой цели можно выделить тактические задачи, такие, как мотивация учебной деятельности с доминированием мотивов ее совершенствования, развитие познавательной самостоятельности; формирование и развитие творческих способностей; усвоение обобщенных и рациональных способов деятельности; формирование опыта самообразования и т. д.
Однако необходимо отметить, что если будет развиваться только стремление к познанию, то это может привести к отрицательным результатам. Люди, у которых развита только эта мотивация и не развита потребность в труде, могут испытывать нежелание работать. Одно из средств решения этих задач на уроках математики — творческие проекты учащихся.
В литературе очень мало разработанных проектов. Статьи, в которых есть методика проведения проектов по математике, включают в себя описание организации проектной деятельности. Рассмотрим некоторые из них.
1.3. Методика организации проектной деятельности школьников в процессе обучения
Как уже отмечалось выше, метод проектов отличается от классических методов обучения. Рассмотрим подробнее организацию проектной деятельности школьников в процессе обучения курсу математики.
Основная цель метода проектов состоит в предоставлении учащимся возможности самостоятельного приобретения знаний в процессе решения практических задач или проблем, требующего интеграции знаний из различных предметных областей.
М.А.Агафонова и О.В.Рыбина выделяют следующие основные цели метода проектов:
научить самостоятельному достижению намеченной цели, а также конструированию полученных знаний;
научить предвидеть мини-проблемы, которые предстоит решить;
сформировать умение ориентироваться в информационном пространстве: находить источники, из которых можно почерпнуть информацию;
получить навыки обработки информации;
сформировать навыки проведения исследований; сформировать навыки работы и делового общения в группе;
сформировать навыки передачи и презентации полученных знаний и опыта.
По мнению Е.Л. Касьяк [24] проектная методика основана на цикличной организации учебного процесса. Отдельный цикл рассматривается как законченный самостоятельный период обучения, направленный на решение определенной задачи в достижении общей цели овладения учебного предмета.
Автор рекомендует перед использованием проектной технологии обучения точно определить цели, к которым будет стремиться выбранный вид деятельности.
Автор выделяет главные цели введения метода проектов в школьную практику:
показать умения отдельного ученика или группы учеников использовать приобретенный в школе исследовательский опыт;
реализовать свой интерес к предмету исследования, приумножить знания о нем;
продемонстрировать уровень обученности по предмету;
подняться на более высокую ступень, образованности, развития, социальной зрелости.
Б.Р. Ниязова и С.И. Горлицкая выделяют следующие цели: способствовать формированию системы знаний и умений, воплощённых в конечный интеллектуальный продукт; содействовать умению логически мыслить; видеть проблемы и принимать решения; заниматься планированием; развивать грамотность и многое другое.
Н.Ю. Пахомова [39] главной целью использования метода проектов называет обучение умениям и навыкам проблематизации, целеполагания, выдвижения гипотез, структурирования и систематизации, планирования и организации мышления и деятельности по решению разнообразных теоретических и практических задач.
Также предлагается считать целью проектной деятельности понимание и применение учащимися знаний, умений и навыков, приобретенных при изучении различных предметов.
К описанию организации работы над проектами существуют различные подходы.
Но большинство авторов считают важным описать деятельность учителя и учащихся на каждом их этапов организации проектной деятельности. Приведем примеры таких описаний.
Обобщим методику работы над проектами, предложенную Н. Мансуровым, Т. Герасимовой, В. Рохловым, и Н.Ю. Пахомовой.
I. Планирование.
Предлагается начать работу над проектом с обсуждения темы будущего проекта. При этом, как уже отмечалось выше, происходит обмен мнениями между участниками проектной деятельности, выдвигаются первые гипотезы, и только после этого предложенные учащимися темы проектов выносится на обсуждение.
Цели первичного обмена мнениями:
Стимулирование потока идей.
Для стимулирования потока идей актуален метод мозговой атаки. Учителю следует по возможности воздержаться от комментариев, записывать на доске идеи, направление работы по мере их высказывания, а также выдвигаемые учащимися возражения.
Учитель предлагает ребятам проблемную ситуацию или задачу, решение которой важно для определенного круга людей, тем самым мотивирую проектную деятельность. Здесь будут уместны чертежи, схемы, плакаты и другие виды наглядных пособий.
Следующим шагом, ребята выделяют проблему, учитель им в этом помогает наводящими вопросами, и пытаются найти возможные способы решения этой проблемы. Когда таких способов предложено достаточно для решения поставленной задачи, учитель предлагает проанализировать каждую из идей.
2. Определение общего направления исследовательской работы.
Когда определены все возможные направления исследований, учитель предлагает учащимся высказать свое отношение каждому из них.
Затем учитель предлагает учащимся поработать над наиболее удачными направлениями; определяет сроки, необходимые для получения конечных результатов; помогает ученикам сформулировать 5-6 связанных друг с другом подтем.
Учителю необходимо продумать вариант объединения выделенных подтем в единый проект для класса (параллели, несколько параллелей и так далее). Каждый участник проекта выбирает ту подтему для будущего исследования, работа над которой буден ему наиболее интересна.
Таким образом формируются группы, работающие по одной подтеме. Задача учителя на данном этапе – проследить, чтобы в каждой создающейся группе работали учащиеся с различным уровнем знаний, творческим потенциалом, различными склонностями и интересами.
Далее учащиеся совместно с учителем выявляют потенциальные возможности каждого (коммуникативные, артистические, публицистические, организаторские, спортивные и т. д.). Учителю следует построить работу так, чтобы каждый мог проявить себя и завоевать признание окружающих.
Можно также выбрать консультантов, т.е. ребят, которые будут помогать исследовательским группам в решении тех или иных задач на тех или иных этапах работы.
Для успешной организации этого этапа учителю рекомендуется: подготовить проблемную задачу, которая бы подтолкнула ребят к обсуждению; рассмотреть возможные способы и сред
ства для поддержания мотивации учащихся (задачи практического характера, наглядные пособия и т.д.), продумать вопросы, которые подтолкнули бы ребят к новой идее, необходимой для осуществления проекта.
В качестве таких вопросов могут быть вопросы, представленные в таблице 2.
Таблица 2. Вопросы, которые может задать учитель участникам проектной деятельности на этапе планирования
| Для выявления уже имеющихся знаний:
| Что вы можете сказать по этой теме (проблеме)? Что вы читали (слышали, изучали на уроках, самостоятельно) по этой теме, проблеме? Как вы относитесь к этой теме (проблеме)? Какие способы решения этой проблемы вы знаете? Что, по- вашему, необходимо для этого сделать? Что еще вы бы хотели изучить (понять), чтобы найти способ решения этой проблемы? |
| Для выявления склонности и интересов учащихся: | Что еще интересно вам было бы узнать в этой области? В чем вы хотели бы лучше разобраться? Ваше любимое занятие вне школы? Чему вы больше всего хотели бы научиться? Кем бы вы хотели стать? В чем вы хотели бы разбираться профессионально? Что бы вы хотели предпринять для осуществления вашего замысла? При каких условиях это было бы возможно? |
| Для выявления затруднений у учащихся:
| О чем (или о ком) вы бы хотели получить более подробную информацию? Что нового вам было бы интересно узнать? В каких вопросах вы бы хотели стать более компетентными? |
| Для определения темы проекта:
| Какие из предложенных тем больше всего отвечают вашим склонностям, интересам? Почему вы предпочли именно эту тему? Каким образом вы могли бы помочь классу (группе) раскрыть эту тему? Какие, по-вашему, существуют критерии итоговой оценки работы над проектом? Как можно определить «программу-максимум» и «программу-минимум»? |
Также учитель должен познакомить учащихся с условиями работы над проектом (количество человек в группах, сроки выполнения проекта); если в работе над проектом принимает участие большое количество человек, то необходимо продумать и организовать несколько направлений работы, при этом обязательно обозначив область рассмотрения каждого из них.
Некоторые методисты рекомендуют завести журнал проекта для записи мероприятий, сроков выполнения определенной деятельности, возникшие вопросы, затруднения, примечания. При этом учитель выступает в роли консультанта и наставника для ребят.
II. Аналитический этап.
Этот этап самостоятельного проведения исследования, получения и анализа информации, во время которого каждый ученик уточняет и формулирует собственную задачу, исходя из цели проекта в целом и задачи своей группы в частности, ищет и собирает информацию, учитывая:
собственный опыт;
результат обмена информацией с другими учащимися, учителями, родителями, консультантами и т.д.;
сведения, полученные из специальной литературы, Интернета и т.д.;
А также анализирует и интерпретирует полученные данные.
На этом же этапе членам группы необходимо договориться о распределении работы и формах контроля работы над проектом. Каждый ученик может вести «индивидуальный журнал», в котором он будет записывать ход работы. Можно вести общий журнал для всех участников проекта.
Это поможет учителю (да и самому ученику) оценить индивидуальный вклад каждого в работу над проектом, а также облегчить контроль. Мы считаем, что ведение индивидуального журнала для ученика зависит от конкретных ситуаций и не является обязательным.
Предлагается следующая последовательность работы:
1. Уточнение и формулировка задач.
Правильная формулировка задачи проекта (т.е. проблемы, которую предстоит решить) предопределяет результативность работы группы. Здесь необходима помощь учителя.
Сначала члены каждой группы обмениваются уже имеющимися знаниями по выбранному ими направления работы, а также соображениями о том, что ещё, на их взгляд, необходимо узнать, исследовать, понять. Затем учитель при помощи проблемных вопросов подводит учащихся к формулировке задачи.
Если учащиеся априорно знают решение поставленной проблемы и легко отвечают на вопросы учителя, задачи для группы поставлены не правильно, так как не отвечают основной цели проекта – обучению навыкам самостоятельной работы и исследовательской деятельности.
Во время работы над проектом учителю необходимо следить, чтобы каждая группа и каждый её член чётко понимали свою собственную задачу, поэтому рекомендуется оформить стенд, на котором были бы вывешены: общие темы проекта, задачи каждой группы, списки членов групп, консультантов, ответственных и т.д.
Такой стенд способствует также осознанию каждым учащимся ответственности за выполняемую работу перед остальными участниками проекта.
2. Поиск и сбор информации.
Здесь учащиеся определяют, где и какие данные им предстоит найти. Затем начинается непосредственно сбор данных и отбор необходимой информации. Этот процесс может осуществляться различными способами, выбор которых зависит от времени, отведённого на данный этап, материальной базы и наличия консультантов.
Учащиеся (с помощью учителя) выбирают способ сбора информации: наблюдение, анкетирование, социологический опрос, интервьюирование, проведение экспериментов, работ со средствами массовой информации, с литературой. Задача учителя – обеспечить, по мере необходимости, консультации по методике проведения такого вида работы.
Здесь необходимо уделить особое внимание обучению учащихся навыкам конспектирования.
На данном этапе учащиеся получают навыки поиска информации её сравнения, классификации; установления связей и проведения аналогий; анализа и синтеза; работы в группе, координации разных точек зрения посредством:
- личных наблюдений и экспериментирования;
- общения с другими людьми (встречи, интервьюирование, опросы);
- работы с литературой и средствами массовой информации.
Учитель играет роль активного наблюдателя: следит за ходом исследований, соответствием цели и задачам проекта; оказывает группам необходимую помощь, не допуская пассивности отдельных участников; обобщает промежуточные результаты исследования для подведения итогов на конечном этапе.
3. Обработка полученной информации.
Необходимое условие успешной работы с информацией – ясное понимание каждым учеником цели работы и критериев отбора информации. Задача учителя – помочь группе определить эти критерии.
Обработка полученной информации – ее понимание, сравнение, отбор наиболее значимой для выполнения поставленной задачи.
Учащимся потребуются умение интерпретировать факты, делать выводы, формировать собственные суждения.
Именно этот этап наиболее труден для учащихся, особенно если они привыкли находить в книгах готовые ответы на все вопросы учителя. Учителю могут помочь в работе вопросы, приведенные в Таблице 3.
Таблица 3. Вопросы, которые может задать учитель на аналитическом этапе
| Определение задач: | Что вам уже известно о теме? Чем конкретно вам будет интересно заниматься в работе над этим проектом? По каким вопросам вы могли бы проконсультировать свою группу (другую группу, весь класс)? Какую помощь вы можете оказать в процессе работы над проектом? Попытайтесь сформулировать задачу так, чтобы все члены вашей группы поняли, какие исследования необходимы для успешной реализации проекта. |
| Поиск и сбор информации: | Какие способы поиска и сбора информации вы знаете? Где можно найти необходимую информацию? Кто может в этом помочь? Кого можно пригласить для консультации? В какие организации можно обратиться за консультацией? Какие конкретно сведения вы там запросите? Какие документы могут содержать нужную вам информацию? Где их можно найти? Подумайте, чем будет заниматься каждый член группы? Какие работы могут выполняться параллельно? Какие исследования требуют больше (меньше) времени? Чем необходимо заняться в первую очередь? В каком порядке будет выполняться работа? Как распределить работу между членами группы? Кто и за что будет отвечать? Где будет проводиться работа? В какие сроки? |
| Интерпретация полученных данных: | Какая информация необходима для решения поставленной задачи? Без какой информации можно обойтись? Обоснуйте ваше мнение. Каковы критерии оценки полученной информации? Установите связь (если она есть) между собранными данными. |
III. Этап обобщения информации.
На этом этапе осуществляются структурирование полученной информации и интеграции полученных знаний, умений, навыков.
При этом учащиеся: систематизируют полученные данные; объединяют в единое целое полученную каждой группой информацию; выстраивают общую логическую схему выводов для подведения итогов.
Это могут быть: рефераты, доклады, проведение конференций, показ видеофильмов, спектаклей; выпуск стенгазет, школьных журналов, презентация в интернете и т.д..
Учителю необходимо проследить, чтобы учащиеся обменивались знаниями и умениями, полученными в процессе различных видов работ с информацией (анкетирование и обработка полученных знаний, проведение социологического опроса, интервьюирование, экспериментальная работа и т.д.).
Все необходимые мероприятия данного этапа должны быть направлены на обобщение информации, выводов и идей каждой группы. Учащиеся должны знать порядок, формы и общепринятые нормы представления полученной информации (правильное составление конспекта, резюме, реферата, порядок выступления на конференции и т.д.).
И на этом этапе учителю необходимо предоставить учащимся максимальную самостоятельность выбора форм представления результатов проекта, поддерживать такие, которые дадут возможность каждому ученику раскрыть свой творческий потенциал.
Если случиться так, что ребята испытывают затруднения в процессе решения какой-либо проблемы, учитель должен прийти им на помощь, но только с личного приглашения ребят. Не следует вмешиваться в их творческий исследовательский процесс без их согласия.
В то же время следует помнить, что пускать все на самотек, допускать стихийную самостоятельность нельзя.
Процесс обобщения информации важен потому, что каждый из участников проекта как бы «пропускает через себя» полученные всей группой знания, умения, навыки, так как в любом случае он должен будет участвовать в презентации результатов проекта.
Варианты вопросов:
Какие данные и выводы целесообразно обобщить и вынести на презентацию?
Кому, по – вашему, будет интересна проблема над которой вы работали?
В какой форме вы хотели бы представить итоги вашей работы? Составьте план.
В чем вы могли бы помочь (исходя из личных склонностей, интересов, способностей) при подготовке презентации итогов проекта?
В чем будет состоять «изюминка» вашей презентации?
Какие формы презентации вы считаете наиболее приемлемыми, и учитывая содержание, цель проекта, возраст и уровень знаний предполагаемой аудитории, а также ваши способности и интересы?
Какие затраты предполагает выбранная форма презентации?
Сколько времени потребуется на подготовку выбранной вами формы презентации?
Чем необходимо заняться в первую очередь? В каком порядке будет выполняться работа? Как она будет распределяться между участниками мероприятия? Кто и за что будет отвечать?
IV. Представление полученных результатов работы (презентация).
На этом этапе учащиеся осмысливают полученные данные и способы достижения результата; обсуждают и готовят итоговое представление результатов работы над проектом (в школе, округе, городе и т.д.).
Учащиеся представляют не только полученные результаты и выводы, но и описывают приемы, при помощи которых была получена и проанализирована информация; демонстрирует приобретенные знания и умения; рассказывают о проблемах, с которыми пришлось столкнуться в работе над проектом.
Любая форма презентации также является учебным процессом, в ходе которого учащиеся приобретают навыки представления итогов своей деятельности.
Основные требования к презентации каждой группы и к общей презентации: выбранная форма должна соответствовать целям проекта, возрасту и уровню аудитории, для которой она проводится.
В процессе работы по обобщению материала и подготовки к презентации у учащихся, как правило, появляются новые вопросы, при обсуждении которых может быть даже пересмотрен ход исследований.
Задача учителя – объяснить учащимся основные правила ведения дискуссий и делового общения; научить их конструктивно относиться к критике своих суждений; признавать право на существование различных точек зрения решения одной проблемы.
Работая над проектом, учителю не следует забывать, что основными критериями успешности являются радость и чувство удовлетворения у всех его участников от осознания собственных достижений и приобретенных навыков. Как видно из вышесказанного степень активности учеников и учителя на разных этапах разная. В учебном проекте ученики должны работать самостоятельно.
Степень активности и самостоятельности учащихся можно представить в виде схемы (см. рис.1).
Рис. 1. Степень активности и самостоятельности учащихся при осуществлении проектной деятельности
Как видим, роль учителя, несомненно, велика на первом и последнем этапах, и от того, как учитель выполнит свою роль на первом этапе – этапе погружения в проект, — зависит судьба проекта в целом. Здесь есть угроза свести работу над проектом к формулированию и выполнению задания по самостоятельной работе учащихся.
На последнем этапе роль учителя велика, поскольку ученикам не под силу сделать обобщение всего того, что они узнали или исследовали, протянуть мостик к следующей теме, прийти, может быть, к неожиданным умозаключениям, которые поможет сделать учитель с его богатым житейским опытом, научным кругозором, аналитическим мышлением.
Как отмечает И.Д. Чечель , на последних этапах проектирования и учащийся, и педагог анализируют и оценивают результаты деятельности, которые часто отождествляются лишь с выполненным проектом.
На самом деле при использовании метода проектов существуют, по крайней мере, два результата. Первый (скрытый) - это педагогический эффект от включения школьников в «добывание знаний» и их логическое применение: формирование личностных качеств, мотивация, рефлексия и самооценка, умение делать выбор и осмыслять как последствия данного выбора, так и результаты собственной деятельности. [18]
Именно эта результативная составляющая часто остается вне сферы внимания учителя, и к оценке предъявляется только сам проект. Поэтому Чечель советует начинающему руководителю проектирования записывать краткие резюме по результатам наблюдений за учащимися, это позволит быть более объективными на самой защите.
Вторая составляющая оценки результата - это сам проект. Причем оценивается не объем освоенной информации (что изучено), а ее применение в деятельности (как применено) для достижения поставленной цели.
Таким образом, обычная пятибалльная система не очень подходит для оценивания проектов. Для оценивания проектов И.Д. Чечель советует использовать рейтинговую оценку. Автор рассматривает два варианта оценки, критерии оценки.
Интересен способ оценки, разработанный доцентом МПГУ П.С. Лернером, который представляет И.Д. Чечель [5].
В ходе анализа методической и педагогической литературы нами проанализированы и выделены параметры оценки результатов проектной деятельности и критерии оценки защиты проекта.
Параметры оценки результатов проектной деятельности:
значимость и актуальность выдвинутых проблем и предлагаемых решений, адекватность их изучаемой тематике;
реальность, практическая направленность и значимость работы;
корректность используемых методов исследования и обработки полученных результатов;
необходимая и достаточная глубина проникновения в проблему, привлечение знаний из других областей;
соответствие содержания целям, задачам и теме проекта;
логичность и последовательность изложения;
четкость формулировок, обобщений, выводов;
аргументированность предлагаемых решений, подходов, выводов;
стилистическая и языковая культура изложения;
полнота библиографии;
наличие собственных взглядов на проблему и выводов;
активность каждого участника проекта в соответствии с его индивидуальными возможностями;
характер общения, взаимопомощи участников в ходе выполнения проекта;
доказательность принимаемых решений, умение аргументировать свои заключения;
авторство;
умение отвечать на вопросы оппонентов, корректность в дискуссии;
перспектива доработки (потенциал);
эстетичность оформления результатов выполненного проекта, качество эскизов, схем, рисунков;
соответствие оформления проекта стандартным требованиям.
Критерии оценки защиты проекта:
качество доклада: композиция, полнота представления работы, подходов, результатов; его объём;
объём и глубина знаний по теме, эрудиция, межпредметные связи;
культура речи;
чувство времени;
использование наглядных средств;
умение удерживать внимание аудитории;
умение отвечать на вопросы: полнота, аргументированность, корректность в дискуссии;
готовность к дискуссии;
доброжелательность, контактность.
Имеется перечень общеучебных умений и навыков, которые развиваются в проектной деятельности.
1. Рефлексивные умения: умение осмысливать задачу, для решения которой недостаточно знаний; умение отвечать на вопрос: чему нужно научиться для решения поставленной задачи?
2. Поисковые (исследовательские) умения:
умение самостоятельно генерировать идеи, т.е. изобретать способ действия, привлекая знания из различных областей;
умение самостоятельно находить недостающую информацию в информационном поле;
умение запрашивать необходимую информацию у эксперта (учителя, консультанта, специалиста);
умение находить несколько вариантов решения проблемы;
умение выдвигать гипотезы;
умение устанавливать причинно-следственные связи.
3. Умения и навыки работы в сотрудничестве:
навыки коллективного планирования;
умение взаимодействовать с любым партнером; навыки взаимопомощи в группе в решении общих задач;
навыки делового партнерского общения;
умение находить и исправлять ошибки в работе других участников группы.
4. Менеджерские умения и навыки:
умение проектировать процесс (изделие);
умение планировать деятельность, время, ресурсы;
умение принимать решения и прогнозировать их последствия;
навыки анализа собственной деятельности (ее хода и промежуточных результатов).
5. Коммуникативные умения:
умение инициировать учебное взаимодействие со взрослыми - вступать в диалог, задавать вопросы и т.д.;
умение вести дискуссию;
умение отстаивать свою точку зрения;
умение находить компромисс;
навыки интервьюирования, устного опроса и т.д.
6. Презентационные умения и навыки:
навыки монологической речи;
умение уверенно держать себя во время выступления;
артистические умения;
умение использовать различные средства наглядности при выступлении;
умение отвечать на незапланированные вопросы.
Видно, что организация проектной деятельности требует от учителя тщательной подготовки, больших временных затрат.
В ходе ее подготовки необходимо соблюдать принципы, требования к проектам, особое внимание уделить интересам и склонностям учащихся, исходя из всего этого, подобрать такой тип проекта, который максимально удовлетворит потребности, склонности, интересы и любознательность учеников.
Но в то же время учитель должен создать условия, способствующие развитию различных качеств и способностей у школьников.
В ходе анализа литературы, нами выявлено, что для успешной реализации проектной деятельности учащихся должны обладать следующими качествами: умение ставить проблемы, выделять цель и задачи своей работы, а также оценивать результат, осуществлять поиск информации, обрабатывать ее, владеть навыками письменной, групповой коммуникации, не бояться публичных выступлений.
1.4 Анализ особенностей изучения величин младшими школьниками как средства формирования их познавательной активности
Особое содержание геометрического материала, включенного в программу и реализованного в системе тщательно отобранных задач, направлено на формирование достаточно полной системы геометрических представлений (включающей образы геометрических фигур, их элементов, отношений между фигурами, их элементами).
На этой основе формируются пространственные представления и воображение, развивается речь и мышление учащихся, организуется целенаправленная работа по формированию важных практических навыков.[15]
Важнейшей задачей учителя является определение методики, раскрывающей содержание геометрического материала на том уровне, который должен быть достигнут учащимся к моменту их перехода в 4 класс, а также ведущих направлений изучение этого материала.
Для формирования геометрических представлений работа должна проводится следующим образом: свойство фигур учащиеся выявляют экспериментально, одновременно усваивают необходимую терминологию и навыки; основное место в обучении должны занимать практические работы учеников, наблюдения и работы с геометрическими объектами.
Оперируя разнообразными предметами, моделями геометрических фигур, выполняя большое число наблюдений и опытов, учащиеся подмечают наиболее общие их признаки (не зависящие от материала, цвета, положения, массы и т.п.).
В методики формировании геометрических представлений важно идти от "вещей" к фигуре (к её образу), а также, наоборот – от образа фигуры к реальной вещи.
Это достигается систематическим использованием приёма материализации геометрических образов. Например, прямая линия не только вычерчивается с помощью линейки, представление о ней даёт и край – ребро линейки, натянутая нить, линии сгиба листа бумаги, линия пересечения двух плоскостей (например, плоскости стены и плоскости потолка).
Отвлекаясь от конкретных свойств материальных вещей, учащиеся овладевают геометрическими представлениями.
Так, например, можно видоизменять способ деления многоугольника отрезком на части. В начале этого может быть перегибание бумажного многоугольника.
В первом классе в основном завершается первоначальное ознакомление с фигурами и их названиями. Это делается на основе рассмотрения окружающих вещей, готовых моделей и изображений фигур. У детей постепенно вырабатывается схема изучения фигур, схема анализа и синтеза, облегчающая усвоение свойств каждой фигуры.
Значительное место в методике должно отводится применению приема сопоставления и противопоставления геометрических фигур. В 1 классе это позволит из множества фигур наглядно выделят множество кругов, множество многоугольников, множество линий и т.д.; во 2 и 3 классах – уточнять свойства фигур, классифицировать их.
Большое внимание следует уделять противопоставлению и сопоставлению плоских фигур (круг – многоугольник, окружность – круг и т.д.), плоских и пространственных фигур (квадрат – куб, круг – шар и пр.)
Уже при первоначальном ознакомлении детей с геометрическими фигурами в 1 классе дети выполняют умственные операции анализа и синтеза.
Важной задачей учителя, определяющей методику обучения в этот момент, является анализ фигуры, на основе которого выделяются ее существенные свойства (признаки) и несущественные.[29]
В процессе обучения возникает потребность применения геометрической и логической терминологии, символики, чертежей.
Так, уже во 2 классе введение буквенной символики помогает не только различать фигуры и их элементы, но и является одним из средств формирования обобщений.
Например, запись ОК
В 1 классе фигуры следует применять наряду с другими материальными вещами как объекты для перечисления. Несколько позже такими объектами должны стать элементы фигур, например вершины, стороны, углы многоугольников.
Учащиеся постепенно знакомятся с измерением отрезков. Это устанавливается прямая связь между отрезками (точками) и числами.
Геометрические фигуры используются при ознакомлении учащихся с долями. В указанных выше случаях открывается больше возможностей органически связать изучение геометрических объектов с арифметическим материалом, включенным в курс математики для 1-3 классов.
Уже в 1-3 классах выполняются простейшие классификации углов (прямые и непрямые), многоугольников (по числу углов) и т.д. Изучение родовых и видовых понятий готовит детей к пониманию определений, построенных на указании рода и видовых отличий.
Использование упражнений, в которых дети отмечают точки, принадлежащие или не принадлежащие фигуре или нескольким фигурам, помогает в дальнейшем трактовать геометрическую фигуру как множество точек.
А это позволяет более осознанно выполнять операции деления фигуры на части или получение фигуры из других (складывание), т.е. выполнять по существу операции объединения, пересечения, добавления над точечными множествами.
Важной общей методической линией осуществления связи в изучении геометрического материала с остальными вопросами курса начальной математики является, таким образом, неявная опора на теоретико-множественные и простейшие логико-математические представления в изучении фигур, их отношений, свойств.
Общим методическим приемом, обеспечивающим прочные геометрические знания, является формирование пространственных представлений через непосредственное восприятие учащимися конкретных реальных вещей; материальных моделей геометрических образов.
В 1 классе пространственные представления вырабатываются в процессе приобретения детьми практического опыта при изучении отношений взаимного положения предметов, выражаемых словами "выше", "ниже", "справа", "сверху", "спереди", "сзади" и т.д.
Во 2-3 классах характер работы по формированию пространственных представлений усложняется.
Например, представления об одной фигуре формируется с опорой на другую. Так, опираясь на представления о треугольнике вообще, можно получить представления о прямоугольном треугольнике.
Результатом обучения в 1-3 классах должно быть формирование первоначальных представлений о точности построений и измерений.
В 1 классе учащиеся овладевают навыками измерения и построения отрезков с помощью линейка (с точностью до 1 см). При этом детям предъявляется не меньшее требования, тем это обычно делается, например, в отношении навыков письма.
Во 2-3т классах в практику измерений и построений постепенно вводятся новые инструменты: циркуль, циркуль – измеритель, чертежный треугольник, рулетка.
Повышаются требования к точности построений и измерений, качеству чертежей и моделей, выполняемых детьми, к описанию хода и результатов проделанной работы.
личина, так же как и число, является основным понятием курса математики начальных классов, в задачу которого входит формирование у детей представления о величине как о некотором свойстве предметов и явлений, которое прежде всего связано с измерением.
В 1-3 классах учащиеся получают представление о таких величинах, как длина, масса, емкость, время, площадь, и о единицах ее измерения. В процессе решения задач они знакомятся с ценой, количеством, стоимостью, скоростью, расстоянием, производительностью и т.д.
В процессе изучения темы важно добиться, чтобы учащиеся научились четко дифференцировать такие тесно связанные между собой, но разные по своей сути понятия, как "величина" и "число".
Хотя формирование представлений о той или иной конкретной величине и о способах ее измерения имеет свои особенности, тем не менее, целесообразно выделить общие этапы, которые имеют место при изучении каждой из величин:[3]
Выяснение и уточнение имеющихся у детей представлений о данной величине (обращение к опыту ребенка).
Сравнение однородных величин (визуально, с помощью ощущений, наложением, приложением, путем использования различных мерок).
Знакомство с единицей измерения данной величины и с измерительным прибором.
Формирование измерительных умений и навыков.
Сложение и вычитание однородных величин, выраженных в единицах одного наименования.
Знакомство с новыми единицами величины, перевод однородных величин, выраженных в единицах одних наименований, в другие, перевод величин, выраженных в единицах одного наименования, в величины, выраженные в единицах двух наименований, и наоборот.
Сложение и вычитание величин, выраженных в единицах двух наименований.
Умножение и деление величины на число.
С целью формирования представлений о разного рода величинах проводятся практические работы, используются упражнения, применяются демонстрационные и индивидуальные наглядные средства, при этом варьируются коллективные, индивидуальные и групповые формы работы на уроке.
Значение с величинами единицами их измерения имеет не только практическое значение: оно предоставляет большие возможности для формирования умения видеть проблему и находить пути ее решения, тем самым способствуя развитию познавательных способностей учащихся.
ГЛАВА 2. ИССЛЕДОВАНИЕ ОСОБЕННОСТЕЙ ПРОЕКТНОЙ ДЕЯТЕЛЬНОСТИ ПРИ ИЗУЧЕНИИ ВЕЛИЧИН В КУРСЕ МАТЕМАТИКИ В НАЧАЛЬНОЙ ШКОЛЕ, КАК СРЕДСТВА ФОРМИРОВАНИЯ ПОЗНАВАТЕЛЬНОЙ АКТИВНОСТИ
2.1. Цели, задачи исследования
На основе анализа педагогической и методической литературы, опыта преподавания математики в школе нами разработана структура проектной деятельности при изучении математики в начальной школе.

Сложность для реализации во время уроков составляют темы с большим информационным объемом, поскольку ученику освоить весь материал за один учебный час будет довольно затруднительно, здесь возможен вариант спаренных уроков или выполнение проекта в виде домашнего задания.
Автор сообщила учащимся, что в конце года вместо итоговой контрольной работы будет оценивать их проекты по данному разделу.
В любом случае эта работа должна включать в себя:
связь с математикой (это будет способствовать поддержанию интереса к предмету, изучению материала, выходящего за рамки школьной программы),
реализацию творческого потенциала учащихся,
обязательно самостоятельную работу школьников, направленную на приобретение новых знаний и умений.
Думаем целесообразным осуществлять проектную деятельность пошагово.
На первом шаге организуем подготовительную работу, цель которой познакомить школьников с сутью проектной деятельности, ее этапами, критериями оценки. Здесь необходимо собрать весь багаж знаний, необходимых для успешной работы над предстоящим проектом.
Цели проекта:
Образовательная: способствовать формированию умения применять математические знания в нестандартных практических задачах.
Развивающая: способствовать развитию мыслительных операций: аналогия, систематизация, обобщение, наблюдение, планирование.
Воспитательная: способствовать поддержанию интереса к предмету, формированию умения трудиться в коллективе.
Учащиеся должны научиться:
ставить цели и задачи проекта,
составлять план работы по выполнению проекта,
разбиваться на группы, распределять роли внутри группы,
определять сроки выполнения проекта,
определять необходимые для реализации проекта материалы, данные и выяснять места, откуда они будут браться,
обобщать полученную информацию, представлять результат проделанной работы.
Количество участников: 10 человек
2.2 Методы и этапы программы исследования
Методика обучения измерению величин
В начальных классах рассматриваются величины: длина, площадь, масса, емкость, время и др. Учащиеся должны получить конкретные представления об этих величинах, ознакомиться с единицами их измерения, овладеть умениями измерять величины, научиться выражать результаты измерения в различных единицах, выполнять арифметические действия над величинами.
Изучение величин имеет большое значение, так как понятие величины является важнейшим понятием математики. Каждая изучаемая величина – это некоторое обобщенное свойство реальных объектов окружающего мира.
Упражнения в измерениях развивают пространственные представления, вооружают учащихся важными практическими навыками, которые широко применяются в жизни. Следовательно, изучение величин – это одно из средств связи обучения с жизнью.
Длина отрезка.
Первые представления о длине как свойстве предметов у детей возникают задолго до школы. К началу обучения в школе дети правильно устанавливают отношения: длиннее – короче, шире – уже, дальше – ближе и т.п., если различия в этом плане ярко выражены, а по другим свойствам предметы сходны.
С первых дней обучения в школе ставится задача уточнять пространственные представления детей. Этому помогают упражнения на сравнение предметов по протяженности, например: "Какая книга тоньше (книги прикладываются друг к другу)?
Кто ниже: Саша или Оля (дети ставятся рядом)? Что глубже: ручей или река (по представлению)? В процессе этих упражнений отрабатывается умение сравнивать предметы по длине, а также обобщается свойство, по которому происходит сравнение – линейная протяженность, длина.
Важным шагом в формировании данного понятия является знакомство с прямой линией и отрезком как "носителем" линейной протяженности. Сравнивая отрезки на глаз, дети получают представление об одинаковых по длине отрезках.
На следующем этапе происходит знакомство с первой единицей измерения отрезков. Из множества отрезков выделяется отрезок, который принимают за единицу. Дети узнают его название и приступают к измерению с помощью этой единицы.
В жизненной практике дети наблюдают чаще всего измерение с помощью метра. Метр – основная единица длины. Метр существует виде отдельного эталона (мерки). С помощью его учитель легко показывает процесс измерения (как откладывается мерка на отрезке, как происходит подсчет единиц измерения). Поэтому некоторые методисты рекомендуют первой единицей измерения вводить метр.
Однако при рассмотрении метра трудно провести достаточное количество упражнений в измерении отрезков так, чтобы работал каждый ученик, что совершенно необходимо для понимания самого процесса измерения.
Другие методисты предлагают ввести первой единицей измерения ввести сантиметр (так дано в программе), что позволит каждому ученику выполнить, сидя за партой большое количество работ по измерению. Это не исключат возможности на подготовительном этапе, опираясь на жизненные наблюдения детей, вспомнить, как и чем измеряют тесьму, ткани, ленту и т.п., отмерить для примера 2 – 3 м шпагата или измерить длину доски.
Не устанавливая соотношений между метром и сантиметром, можно ввести сантиметр как мерку измерения небольших отрезков, длина которых меньше метра.
Чтобы дети получили наглядное представление о сантиметре, следует выполнить ряд упражнений. Например, полезно, чтобы они сами изготовили модели сантиметра (нарезать из узкой полоски бумаги в клетку полоски длиной 1 см), начертили отрезки длиной 1 см в тетрадях (по клеточкам), нашли, что ширина мизинца примерно равна 1 см.
Далее учащихся знакомят с измерением отрезков. Чтобы дети ясно поняли процесс измерения и что показывают числа, получаемые при измерении, целесообразно постепенно переходить от простейшего приема укладывания моделей сантиметра и их подсчета к более трудному – отмериванию ("прошагать меркой по отрезку и подсчитать, сколько раз отложилась единица измерения). Только затем приступать к измерению способом прикладывания линейки или рулетки к измеряемому отрезку.
Многие методисты (Н.С. Попова, П.С. Исакова, А.М. Пышкало и др.) советуют сначала пользоваться линейками, которые изготавливаются детьми из листа бумаги в клеточку.
На этих листах наносятся сантиметровые деления, но цифры не пишутся. Пользуясь этими линейками, дети измеряют отрезки, чертят отрезки на нелинованной бумаге, показывают отрезки заданной длины на самой линейки.
При работе с масштабной линейкой обращается внимание на правильность положения линейки при измерении (начало отрезка должно совпадать с нулевым делением на линейке).
Следует научить детей выполнять округление результатов измерения: если сантиметр уложился 5 раз и остался отрезок, меньше половины сантиметра, то его отбрасывают и называют длину отрезка так: "немного больше 5 см", "около 5 см"; если остался отрезок, который равен половине сантиметра или больше, то его засчитывают за целый сантиметр и результат измерения называют так: "немного дольше 6 см", "приблизительно 6 см".
Для формирования измерительных навыков включается система разнообразных упражнений. Это измерение и черчение отрезков; сравнение отрезков, чтобы ответить на вопрос: на сколько сантиметров длиннее один отрезок, чем другой; увеличение и уменьшение их на несколько сантиметров. В процессе этих упражнений у учащихся формируется понятие длины как числа сантиметров, которые укладываются в данном отрезке.
Позднее, при изучении нумерации чисел в пределах 100, вводятся новые единицы измерения – дециметр, а затем метр. Работа проходит в таком же плане, как и при знакомстве с сантиметром.
Затем устанавливают отношения между единицами измерения (сколько сантиметров содержится в 1 дм, в 1м, сколько дециметров в 1 м). дети упражняются в измерении с помощью двух различных мерок (например, длина крышки парты 4дм 5см, длина доски 2м 8 дм). С этого времени приступают к сравнению длин на основе сравнения соответствующих отрезков.
Затем рассматривают преобразование величин: замену крупных единиц мелкими (3дм 5 см = 35см) и мелких единиц крупными (48см = 4дм 8 см).постепенно учащиеся осознают, что числовое значение длины зависит от выбора единицы измерения (например, длина одного и того же отрезка может быть обозначена и как 3 дм, и как 30см).
Сравнение двух длин, выраженных в единицах двух наименований, теперь выполняют на основе преобразования их и сравнения числовых значений, при которых стоят одинаковые наименования единиц измерения (4дм 8см 39см, так как 48см 39см, или 4дм 8см 3дм 9см).
Во II классе знакомство с единицами длины продолжается: дети знакомятся с миллиметром, а позднее с километром.
Введение миллиметра обосновывается необходимостью измерять отрезки, меньше 1см. наглядное представление о миллиметре дети получают, рассматривая деление на обычной масштабной линейке или на миллиметровой бумаге.
Сразу же устанавливается, сколько миллиметров содержится в 1 с, и дети приступают к измерениям с точностью до миллиметра (с помощью циркуля, а также с помощью линейки).
При этом особое внимание обращается на то. Чтобы дети правильно располагали глаз при совмещении концов отрезка с делениями на шкале линейки. Для формирования измерительных навыков включаются упражнения на измерения не только на уроках математики, но и на других уроках.
При знакомстве с километром полезно произвести практические работы на местности, чтобы сформировать представление об этой единицы измерения. Чаще всего дети с учителем проходят расстояние, равное 1км (или 500м). измеряют пройденное расстояние либо шагами (2 шага примерно составляют 1м), либо с помощью рулетки или мерной веревки.
Попутно дети упражняются в определении некоторых расстояний на глаз. Если есть возможность, проводят экскурсию на автобусный или железнодорожный вокзал, чтобы узнать данные о расстояниях до ближайших населенных пунктов и городов. Этот материал потом используется на уроках при составлении задач.
В III классе учащиеся составляют и заучивают таблицу всех изученных единиц длины и их отношений.

Таблица усваивается в процессе многократных и систематических упражнений вида: сколько метров в 1 км? Во сколько раз метр дольше дециметра? На сколько сантиметров 1 м больше, чем 1 см? Сколько метров составляет половина километра? Четверть километра? Десятая часть километра? и т.п. кроме того, продолжается работа по преобразованию и сравнению длин, выраженных в единицах двух наименований, изучаются письменные приемы вычислений над ними.
Начиная со II класса дети в процессе решения задач знакомятся с нахождением длины косвенным путем. Например, зная длину одного класса и число классов на одном этаже, вычисляют длину здания школы; зная высоту комнат и количество этажей дома, можно вычислить приблизительно высоту дома и т.п.
Позднее, в III классе, после ознакомления со скоростью движения и изучения связи между величинами скорость – время – расстояние, учащиеся узнают о том, что можно вычислять расстояние, зная скорость и время движения.
В методике работы над площадью фигуры имеется много общего с работой над длиной отрезка.
Прежде всего, площадь выделяется как свойство плоских предметов среди других их свойств. Уже дошкольники сравнивают предметы по площади и правильно устанавливают отношения "больше", "меньше", "равно", если сравниваемые предметы резко отличаются друг от друга или совершенно одинаковые. [20]
При этом дети пользуются наложением предметов или сравнивают их на глаз, сопоставляя предметы по занимаемому месту на столе, на земле, на листе бумаги и т.п. однако, сравнивая предметы, у которых форма различна, а различие площадей не очень четко выражено, дети испытывают затруднения.
В этом случае они заменяют сравнение по площади сравнением по длине или по ширине предметов, т.е. переходят на линейную протяженность, особенно в тех случаях, когда по одному из измерений предметы сильно отличаются друг от друга.
В процессе изучения геометрического материала в I – II классах у детей уточняются представления о площади как о свойстве плоских геометрических фигур. Более четким становится понимание того, что фигуры могут быть различными и одинаковыми по площади.
Этому способствуют упражнения на вырезание фигур из бумаги, черчение и раскрашивание их в тетрадях и т.п. В процессе решения задач с геометрическим содержанием учащиеся знакомятся с некоторыми свойствами площади. Они убеждаются, что площадь не изменяется при изменении положения фигуры на плоскости (фигура не становится ни больше, ни меньше).
Дети многократно наблюдают соотношение между всей фигурой и ее частями (часть меньше целого), упражняются в составлении различных по форме фигур из одних и тех же заданных частей (т.е. построение равносоставленных фигур).
Учащиеся постепенно накапливают представления о делении фигур на неравные равные части, сравнивая наложением полученные части, сравнивая наложением полученные части. Все эти знания и умения дети приобретают практическим путем попутно с изучением самих фигур.
Ознакомление с площадью можно провести так:
"Посмотрите на фигуры, прикрепленные к доске, и скажите, какая из них занимает больше всего места на доске (квадрат AMKD занимает места больше всех фигур). В этом случае говорят, что площадь квадрата больше, чем площадь каждого треугольника и квадрата CDMB. Сравните площадь треугольника АВС и квадрата AMKD (площадь треугольника меньше, чем площадь квадрата).
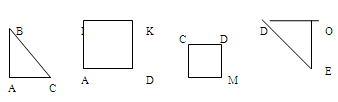
Эти фигуры сравниваются наложением – треугольник занимает только часть квадрата, значит, действительно площадь его меньше площади квадрата. Сравните на глаз площадь треугольника ФВС и площадь треугольника DOE (у них площади одинаковые, они занимают одинаковое место на доске, хотя расположены по-разному). Проверьте наложением.
Аналогично сравниваются по площади другие фигуры, а также предметы окружающей обстановки.
Однако не всегда так легко установить, какая из двух фигур имеет большую (меньшую) площадь или они одинаковы по площади. Чтобы показать это учащимся, можно предложить им сравнить вырезанные из бумаги прямоугольник и квадрат, незначительно отличающиеся по площади, например: размеры квадрата 4х4 дм, а прямоугольника 5х3 дм, при этом фигуры с обратной стороны разбиты на квадратные дециметры. [7]
Сначала учащиеся пытаются сравнить эти фигуры на глаз, а также путем наложения. Однако оба способа не помогают детям решить вопрос убедительно. Выслушав различные предположения, учитель поворачивает фигуры той стороной, на которой сделана разбивка на квадраты, и предлагает сосчитать, сколько одинаковых квадратов содержит каждая фигура.
На этой основе дети устанавливают, площадь какой фигуры больше, а какой меньше. Аналогичные упражнения на сравнивание площади фигур, составленных из одинаковых квадратов, выполняются по учебнику, а также по чертежам, данным на доске. Дети убеждаются в том, что если фигуры состоят из одинаковых квадратов, то площадь той фигуры больше (меньше), которая содержит больше (меньше) квадратов.
Полезно на этом же уроке рассмотреть такой случай, когда разные по форме фигуры имеют одинаковую площадь, так как содержат одинаковое число квадратов. На последующих уроках включаются упражнения на подсчет квадратов, содержащихся в заданных фигурах, предлагается начертить в тетрадях фигуры, которые состоят из заданного числа квадратов (клеточек тетради).
В процессе таких упражнений начинает формироваться понятие о площади как о числе квадратных единиц, содержащихся в геометрической фигуре.
На следующем этапе учащихся знакомят с первой единицей площади – квадратным сантиметром . Учащиеся чертят в тетрадях, вырезают из бумаги в клеточку квадраты со стороной 1см. учитель сообщает: "это единица площади – квадратный сантиметр". Используя бумажные модели квадратного сантиметра, дети составляют из них различные геометрические фигуры и находят подсчетом их площадь.
Сравнивая площади составленных фигур, дети еще раз убеждаются, что площадь той фигуры больше (меньше), которая содержит больше (меньше) квадратных сантиметров. Площади фигур содержащих одинаковое число квадратных сантиметров, равны, хотя фигуры могут не совмещаться наложением.
Эффективен на этом этапе прием сопоставления знакомых детям величин – длины отрезка и площади фигуры, который помогает предупредить смещение этих величин. Выполняя конкретные упражнения, обнаруживают некоторое сходство и существенное различие этих величин: сантиметр – единица длины; квадратный сантиметр – единица площади; длина отрезка – число сантиметров, которые содержаться в данном отрезке; площадь фигуры – число квадратных сантиметров, содержащихся в этой фигуре.
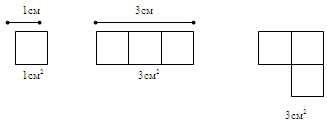
В дальнейшем наглядное представление о квадратном сантиметре и понятие о площади фигур закрепляются. Включаются упражнение на площади фигур, разбитых на квадратные сантиметры. Предлагается при подсчете квадратных сантиметров группировать их по рядам или столбцам, чтобы ускорить нахождение их общего числа.
Рассматриваются и такие фигуры, которые на ряду с целыми квадратными сантиметрами содержат и нецелые – половины, а также доли больше или меньше, чем половина квадратного сантиметра.
Следует также ознакомить учащихся с нахождением приближенной площади фигуры таким способом: сосчитать все нецелые квадратные сантиметры и общее число их разделить на два, затем полученное число сложить с числом целых квадратных сантиметров, которые содержатся в данной фигуре.
Для нахождения площади геометрических фигур, не разделенных на квадратные сантиметры, используют палетку. Палетка – это прозрачная пластинка, разбитая на равные квадраты. Сетка может быть нанесена на кальку или состоять из нитей, натянутых на рамку.
На данном этапе используют палетку, каждое деление которой равно квадратному сантиметру.[36]
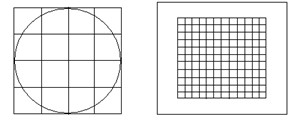
Наложив палетку на геометрическую фигуру, подсчитывают число целых и нецелых квадратных сантиметров, которые в ней содержатся. Для нахождения площади фигур, начерченных в тетрадях, в качестве палетки используют разлиновку тетрадей. Каждый раз подчеркивают, что найденная площадь равна приблизительно такому – то числу (около 20 см2).
В это же время приступают к сопоставлению площади и периметра многоугольников с тем, чтобы дети не смешивали эти понятия, а дальнейшем четко различали способы нахождения площади и периметра прямоугольника. Выполняя практические упражнения с геометрическими фигурами, дети подсчитывают число квадратных сантиметров и тут же измеряют периметр многоугольника в сантиметрах.
На следующем этапе учащиеся знакомятся с приемом вычисления площади прямоугольника (квадрата) (Приложение №2). Сначала рассматривают прямоугольники, которые уже разделены на квадратные сантиметры.
Их площадь находят путем подсчета квадратных сантиметров в одном ряду, а затем полученном число умножают на число рядов. Очень важно при этом установить соответствие между длиной прямоугольника и числом квадратных сантиметров, прилегающих к длине; шириной прямоугольника и числом рядов.
Затем дети чертят прямоугольник по заданным длинам сторон, разбивают его на ряды, а один ряд на квадраты и снова убеждаются в соответствии: если длина 4 см, то в одном ряду, прилегающем к этой стороне, содержится 4 кв.см, если ширина 3 см, то таких радов оказывается 3. число квадратных сантиметров равно произведению чисел 4 и 3. делается вывод: чтобы вычислить площадь прямоугольника, нужно знать его длину и ширину (в одинаковых единицах) и найти произведение этих чисел (Приложение № 1, 2).
В процессе решения задач на вычисление площади и периметра прямоугольников следует показать, что фигуры, имеющие одинаковую площадь, могут иметь неодинаковый периметры, и что фигуры, имеющие одинаковые периметры, могут иметь неодинаковые площади.
Например, это легко наблюдать при заполнении таблицы вида:
| Длина | 7 см | 6 см | 5 см | 4 см |
| Ширина | 1 см | 2 см | 3 см | 4 см |
| Периметр | 16 см | 16 см | 16 см | 16 см |
| Площадь | 7 см2 | 12 см2 | 15 см2 | 16 см2 |
Далее учащиеся знакомятся с дм2. Как и при введении см2, прежде всего формируется наглядный образ новой единицы: дети чертят на клетчатой бумаге квадрат со стороной 1 дм и затем вырезают его, составляют фигуры из нескольких квадратных дециметров, называя их площадь и периметр.
Устанавливается соотношение между квадратным дециметром и квадратным сантиметром: 1 дм2 = 100 см2. для этого просто вычисляется площадь квадрата со стороной 1 дм = 10 см (10*10 = 100). Учащиеся сами вычисляют площадь квадрата со стороной 1 дм в квадратных сантиметрах и записывают: 1 дм2 = 100 см2 затем дети учатся заменять мелкие единицы крупными и наоборот.
Для достижения возможности решать задачи с данными, полученными путем непосредственных измерений при выполнении практических работ, необходимо выполнить ряд упражнений: "Выразить в см2: 2 дм2; 1 дм2 74 см2 и т.п. Выразить в дм2 и см2: 570 см2; 1250 см2".
На следующем этапе аналогично рассматривается квадратный метр. Обращается особое внимание на решение практических задач . Должна быть составлена и усвоена таблица всех изученных единиц площади и их отношений.
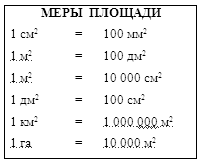
Наряду с решением задач на нахождение площади прямоугольника по данным длине и ширине решают обратные задачи на нахождение одной из сторон по известной площади и другой стороне прямоугольника.
2.3 Анализ результатов
В ходе этого занятия учащиеся познакомились с правилами, этапами работы над проектами, с видами проектов и критериями их оценивания. Для реализации был выбран метод беседа, учащиеся осваивали новую для них информацию, отвечая на вопросы учителя.
Первым вопросом был: Что такое проект? Учащиеся отвечали совершенно неожиданно. Одни говорили, что это схема (приводя в пример проект дома), другие, что это шоу из телевидения (имея в виду «Фабрику звезд»), третьи – что это план выполнения каких-то действий.
Обобщая и дополняя полученные «определения», совместно пришли к выводу. Что проект – это самостоятельная творческая работа учащегося, выполненная от идеи до ее воплощения в жизнь с помощью консультаций учителя.
Принимали ли вы когда-нибудь в них участие? Это был второй вопрос к ребятам. Школьники сказали, что никогда не участвовали в организации проекта, то есть у них не было опыта проектной деятельности. Но им были знакомы некоторые проекты из повседневной жизни. В качестве примеров приводили различные проекты телевидения.
Отвечая на вопрос, как организовывается работа над проектом, учащиеся испытали затруднения. Сначала мы вместе с ними выяснили, что существует несколько этапов. Их жизненный опыт подсказывал, что сначала надо спланировать всю работу. В ходе беседы, отвечая на вопросы, учащиеся следующим этапом назвали работу над выполнением проекта.
Здесь было предложено разбить этот этап на два: аналитический и этап обобщения полученной информации.
Исходя из названий этапов, ребята смогли самостоятельно определить вид деятельности на каждом из них. И последним этапом учащиеся назвали этап представления результатов.
Они попытались самостоятельно предложить возможные варианты презентаций. На этом этапе занятия затруднений не возникло.
Следующим шагом рассмотрены виды проектов. Ребятам были предложены основания для классификаций и учащиеся пробовали самостоятельно определить эти проекты. У них не всегда это получалось, тогда предлагались сами названия видов проекта, и учащиеся рассуждали о сущности этого вида.
На этом теоретический блок занятия закончился. Учащимся были выданы брошюрки «Проектное портфолио», в которых зафиксирован основной теоретический материал по проектной деятельности. Ребята познакомились с критериями оценивания.
Анализируя проведенное занятие, можно сказать, что у учащихся возник интерес. Они активно принимали участие в беседе, интересовались, что именно будут они делать на следующих занятиях, рассказывали о своем прошлом опыте проектной деятельности.
Задание 2
Цель занятия: сформировать у учащихся умение описывать работу над проектом на каждом этапе. На этом занятии ученики попробовали себя в проектной деятельности по математики. Они применили полученные на прошлом занятии теоретические знания на практике.
Чтобы успешнее это сделать, с ребятами была проведена работа по теоретическому блоку, здесь они могли обратиться за помощью к брошюре, если испытывали затруднения.
Каждый шаг организации проектной деятельности имел вполне определенную цель. Так, целью первого шага было познакомить школьников с сутью проектной деятельности, ее этапами, критериями оценки, провести закрепление полученного теоретического блока знаний на практике.
Эта цель была достигнута и реализована, поскольку учащиеся успешно самостоятельно организовали работу над проектом «Расчет затрат на еду в месяц семьей из 3 человек», на презентации осознанно оперировали полученными теоретическими знаниями.
Но здесь нельзя говорить о том, что учащиеся овладели прочными умениями и навыками, так как продолжительность этого этапа мала, и он не включал в себя весь объем материала по проектной деятельности.
Теоретический блок материала. Изложенного на данном этапе содержал лишь необходимые данные для организации проектной деятельности в рамках кружка по математике.
Цель второго шага нашей работы заключалась в осуществлении работы над проектом «Строительство дачи». Цель была достигнута, поскольку учащимися выполнен предложенный проект на достаточно высоком уровне. Деятельность школьников носила самостоятельный и творческий характер.
Учитель на этом этапе выступал в роли консультанта, наставника, его задачей на данном этапе была организация деятельнос
ти учащихся в соответствии с этапами проектной деятельности и не допустить стихийный характер самостоятельности учащихся. Д
ополнительной целью для себя мы выдвинули: определить, насколько сформированы умения ставить проблемы, выделять цель и задачи своей работы, а также оценивать результат, осуществлять поиск информации, обрабатывать ее; навыки письменной, групповой коммуникации, умение вести себя в публичном выступлении. Эта цель была реализована на последнем девятом занятии кружка.
На каждом занятии учащимся предлагалась анкета, по ответам на которую получены следующие результаты.
Всем участникам кружка понравилось осуществлять проектную деятельность.
Можно посмотреть тенденцию развития интереса школьников к проектной деятельности на предложенной ниже диаграмме. Причем, если ученик отвечал не уверенное «да», то мы считали ответ отрицательным.
Диаграмма «Развитие познавательной активности школьников к проектной деятельности»
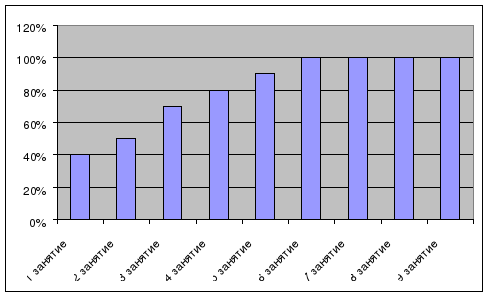
Отвечая на второй вопрос анкеты, ребята говорили, что проведенные занятия дали им:
Возможность ознакомиться с процессом разработки плана садового участка;
Знания и умения из области проведенных расчетов;
Позволили увидеть реальность осуществления идеи проекта;
Знания по решению задачи, не знакомые ранее;
Знания по проектной деятельности;
Умение составлять план предстоящей работы;
Воплощать идеи в реальность;
Умение работать с информацией.
В качестве предложений ребята выдвинули идеи об организации проектной деятельности во время уроков, предложили темы проектов.
Критерии эффективности проведенной работы определялись на основе формирования умений, представленных в таблице.
Критерии сформированности умений
| Решение проблемы |
| Постановка проблемы |
| Уровень I | называет причины, по которым он приступил к работе над проектом |
| Уровень II | описывает идеальную с его точки зрения (желаемую) ситуацию |
| Уровень III | самостоятельно формулирует противоречие между реальной и идеальной ситуацией, обращая его в проблему с помощью учителя |
| Уровень IV | самостоятельно формулирует проблему на основе анализа ситуации |
| Целеполагание и планирование |
| Уровень I | демонстрирует понимание цели проекта, выработанной совместно с учителем |
| Уровень II | самостоятельно ставит задачи на основе цели, сформулированной с помощью учителя |
| Уровень III | самостоятельно ставит цель проекта на основании проблемы, оценивает промежуточные результаты |
| Уровень IV | предлагает стратегию (технологию, процедуру) достижения цели на основе анализа альтернатив; |
| Оценка результата |
| Уровень I | сравнивает полученный продукт с его описанием |
| Уровень II | определяет соответствие полученного продукта запланированному, на основе заранее заданных критериев |
| Уровень III | дает рекомендации по использованию полученного продукта, обоснованно указывает на сильные стороны своей работы, анализирует причины неудач |
| Уровень IV | определяет возможные дальнейшие действия, связанные с полученным продуктом, оценивает степень достижения цели выступления на основе обратной связи с аудиторией |
| Работа с информацией |
| Поиск информации |
| Уровень I | следует технологии работы с конкретным источником информации, предложенной учителем |
| Уровень II | определяет, какие его знания могут быть использованы при работе над проектом, определяет «белые пятна» в имеющейся информации, |
| Уровень III | определяет общее направление поиска и возможные источники недостающей информации |
| Уровень IV | указывает противоречия или неполноту информации, которой он располагает на предпроектном этапе |
| Обработка информации |
| Уровень I | делает выводы, касающиеся темы проекта, аргументируя их на основе полученной информации |
| Уровень II | определяет необходимость той или иной информации для реализации проекта |
| Уровень III | делает самостоятельные выводы на основе полученной информации с использованием основных логических операций (анализ, синтез, аналогия) |
| Уровень IV | делает аргументированный вывод на основе информации |
| Коммуникация |
| Публичное выступление |
| Уровень I | готовит выступление и грамотно рассказывает о цели, ходе или результатах работы по проекту, отвечает на уточняющие вопросы |
| Уровень II | делает публичное выступление о цели, ходе, результатах проекта, обращает аудиторию к наглядным материалам, отвечает на вопросы, нацеленные на понимание содержания выступления. |
| Уровень III | самостоятельно ставит цель публичного выступления, использует средства невербального воздействия на аудиторию, отвечает на вопросы |
| Уровень IV | демонстрирует владение способами воздействия на аудиторию, отвечает на вопросы, направленные на дискредитацию его позиции, организует обратную связь с аудиторией |
| Письменная коммуникация |
| Уровень I | соблюдает правила оформления документов (материалов, выводов и т.п.), предложенные учителем |
| Уровень II | демонстрирует владение способами представления информации в различных формах (текст, графики, схемы, таблицы и т.п.) |
| Уровень III | Определяет цель и аудиторию для предъявления информации |
| Уровень IV | Самостоятельно определяет адекватные форму и структуру представления информации и носители информации, в зависимости от цели ее предъявления и предполагаемых потребителей продукта. |
| Решение задачи практического характера |
| Уровень I | умение не сформировано. Задача не решена |
| Уровень II | задача решена, учащийся затрудняется обосновать решение или даны верные рассуждения, но ответ задачи неверный |
| Уровень III | задача решена верно, даются пояснения по ходу решения не всегда верные |
| Уровень IV | задача решена верно, даны пояснения всем этапам решения |
К предложенным критериям нами добавлен критерий сформированности решения задачи практического характера на оптимизацию.
Анализируя последнее занятие , его результаты и работы учащихся получены следующие результаты:
Сформированность умения ставить проблему
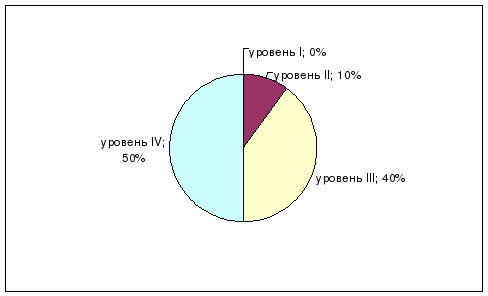
Сформированность умения определять цель и задачи работы
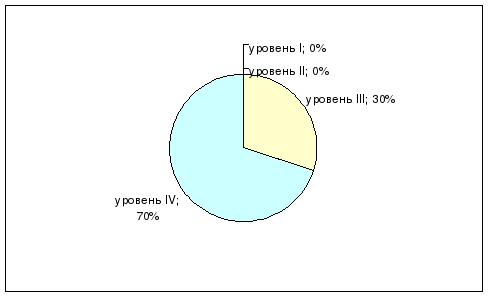
Сформированность умения определять результат проектной деятельности:
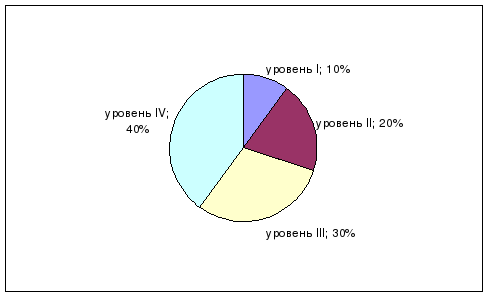
Сформированность умения осуществлять поиск информации
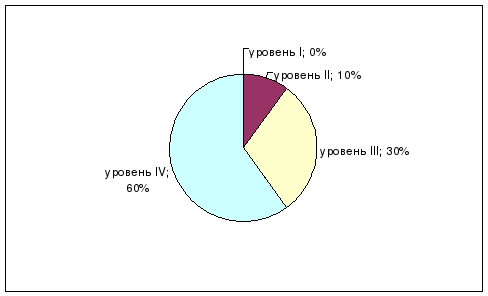
Сформированность умения обрабатывать информацию

Качество публичного выступления
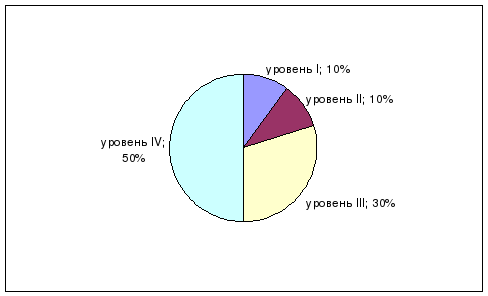
Качество письменного оформления проекта
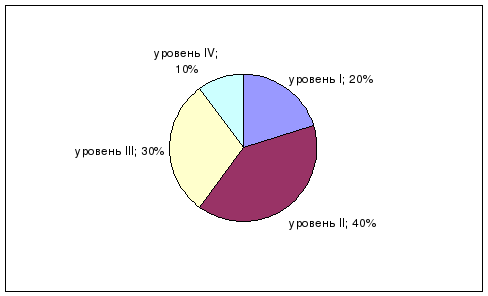
Решение задач практического характера
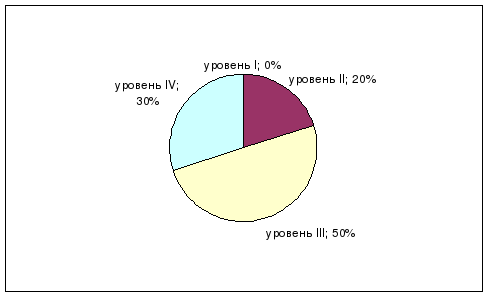
Из вышеприведенных диаграмм видно, что все участники проектной деятельности в той или иной мере овладели умениями, формируемыми в процессе реализации проектной деятельности. У всех учащихся сформировалось умение решать простейшую задачу на максимизацию.
Таким образом, можно сказать, что организованная проектная деятельность дала положительные результаты.
Для полного формирования рассмотренных актиуности считаем необходимым, включать элементы проектной деятельности в процесс обучения математике, это удобнее реализовать в цикле внеклассных мероприятий.
Проведенная нами работа имеет логическое продолжение, поскольку способствует развитию таких умений и качеств личности ученика, которые необходимо найдут применение в повседневной практической жизни ребенка, в курсе изучения многих других дисциплин.
Т. Громова, О. Быкова процесс работы над созданием творческого проекта представляют в виде таблицы
| Этап работы над проектом | Содержание работы | Деятельность учащихся | Деятельность учителя |
| 1. Подготовка | а) Определение темы и целей проекта, его исходного положения; б) Подбор рабочей группы | Обсуждают тему проекта с учителем и получают при необходимости дополнительную информацию. Определяют цели проекта. | Знакомят со смыслом проектного подхода и мотивирует учащихся. Помогает в определении цели проекта. Наблюдает за работой учеников. |
| 2. Планирование | а) Определение источников необходимой информации; б) Определение способов сбора и анализа информации; в) Определение способа представления результатов (Формы проекта); г) Установление процедур и критериев оценки результатов проекта; д) Распределение задач (обязанностей) между членами рабочей группы | Формулируют задачи проекта. Вырабатывают план действий. Выбирают и обосновывают критерии успеха проектной деятельности. | Предлагает идеи, высказывает предложения. Наблюдает за работой учащихся. |
| 3. Исследование | а) Сбор и уточнение информации (основные инструменты: интервью, опросы, наблюдения, эксперименты и т.д.); б) Выявление («мозговой штурм») и обсуждение альтернатив, возникающих в ходе выполнения проекта; в) Выбор оптимального варианта хода проекта; г) поэтапное выполнение исследовательских задач | Поэтапно выполняют задачи проекта. | Наблюдает, советует, руководит деятельностью учащихся. |
| 4. Выводы | а) Анализ информации; б) Формулирование выводов | Выполняют исследование и работают над проектом. Анализируя информацию. Оформляют проект. | Наблюдает, советует (по просьбе учащихся). |
| 5. Представление (защита) проекта и оценка его результатов | а) Подготовка отчета о ходе выполнения проекта с объяснением полученных результатов (возможные формы отчета: устный отчет с демонстрацией материалов, письменный отчет); б) Анализ выполнения проекта, достигнутых результатов (успехов и неудач) и причин этого | Представляют проект, участвуют в его коллективном анализе и оценке. | Слушает, задает вопросы в роли рядового участника. При необходимости направляет процесс анализа. Оценивает усилия учащихся, качество отчета, креативность, качество использования источников, потенциал продолжения проекта. |
И в виде последовательности шестнадцати шагов, на каждом из которых выделена ведущая роль учеников и учителя.
Формулировка учителем темы проекта (учитель) → Выбор возрастной категории учащихся (учитель) → Формулировка основополагающего вопроса и проблемных вопросов учебной темы (учитель) → Формулировка дидактических целей проекта (учитель) → Формулировка дидактических задач (учитель) → Формулировка проблемы или выбор темы индивидуальных исследований учащихся (учащиеся) → Выдвижение гипотез решения проблемы (учащиеся) → Определение творческого названия проекта (учащиеся вместе с учителем) → Формирование групп для проведения исследований и определение формы представления результатов (учащиеся) → Обсуждение плана работы учащихся индивидуально или в группе (учащиеся) → Обсуждение со школьниками возможных источников информации, вопросов защиты авторских прав (учитель совместно с учениками) → Самостоятельная работа учащихся в группах, обсуждение задания каждого в группе (учащиеся, учитель - консультант) → Самостоятельная работа групп (учащиеся, учитель - консультант) → Подготовка учащимися презентации по отчету о проделанной работе (учащиеся) → Защита полученных результатов и выводов (учащиеся) → Оценивание результатов проекта школьниками и учителем (учащиеся с учителем).
Пахомова Н.Ю. , деятельность каждого участника проектной работы на разных этапах представляют также в виде таблицы.
| Учитель | Учащиеся |
| 1-й этап – погружение в проект |
| Формулирует: (формулирование учебного проекта производится с учетом возраста учащихся) | Осуществляют |
| 1) проблему проекта; | 1) личностное присвоение проблемы; |
| 2) сюжетную ситуацию; | 2) вживание в ситуацию; |
| 3) цель и задачи; | 3) принятие, уточнение и конкретизация цели и задач; |
| 2-й этап – организация деятельности |
| Организует деятельность – предлагает (оснащает всем необходимым и создает условия для самостоятельной работы): | Осуществляют: |
| 4) организовать группы; | 4)разбивку на группы; |
| 5) распределить амплуа в группах; | 5)распределение ролей в группе; |
| 6) спланировать деятельность по решению задач проекта; | 6)планирование работы; |
| 7) возможные формы презентации результатов. | 7)выбор формы и способа презентации предполагаемых результатов. |
| 3-й этап – осуществление деятельности |
| Не участвует, но: | Работают активно и самостоятельно: |
| 8) контролирует учащихся по необходимости; | 8) каждый в соответствии со своим амплуа и сообща; |
| 9) ненавязчиво контролирует; | 9) консультируются по необходимости; |
| 10) дает новые знания, когда у учащихся возникает в этом необходимость; | 10) «добывают» недостающие знания; |
| 11) репетирует с учениками предстоящую презентацию результатов. | 11) подготавливают презентацию результатов. |
| 4-й этап – презентация |
| Принимает отчет | Демонстрируют |
| 12) обобщает и резюмирует полученные результаты; | 12) понимание проблемы, цели и задач; |
| 13) подводит итоги обучения; | 13) умение планировать и осуществлять работу; |
| 14) оценивает умения: общаться, слушать, обосновывать свое мнение, толерантность и т.д. | 14) найденный способ решения проблемы; |
| 15) акцентирует внимание на воспитательном моменте: умении работать в группе на общий результат и т.д. | 15) рефлексию деятельности и результата; |
|
| 16) дают взаимооценку деятельности и ее результативности. |
Автор в своей работе подробно рассматривает весь ход осуществления проектной деятельности. Особое внимание уделяет рассмотрению организации первого этапа осуществления проектной деятельности, поскольку именно в ходе реализации этого этапа у учителя возникают наибольшие затруднения.
Оценивать проектную деятельность И.Д. Чечель предлагает по двум направлениям:
1. Индивидуальный проект. Перед защитой на каждого учащегося составляется индивидуальная карта. В ходе защиты она заполняется педагогом и одноклассниками. После этого подсчитывается среднеарифметическая величина из расчета баллов, выставленных в таблице.
|
| Достигнутый результат | Оформление (из 15 баллов) | Защита | Процесс проектирования |
| Представление (из 15 баллов) | Ответы на вопрос (из 15 баллов) | Интеллектуальная активность (из 10 баллов) | Творчество (из 10 баллов) | Практическая деятельность (из 10 баллов) | Умение работать в команде (из 10 баллов) |
| Самооценка |
|
|
|
|
|
|
|
|
| Педагог |
|
|
|
|
|
|
|
|
| Коллеги по команде (классу) |
|
|
|
|
|
|
|
|
Суммирование в этом случае выглядит следующим образом:
85 - 100 баллов - «5»;
70 - 85 баллов - «4»;
50 - 70 баллов - «3»;
менее 50 баллов - «2».
Если ученик получает двойку, то, конечно же, проектирование повторить невозможно, нет времени, но оставлять такой пробел просто недопустимо. Итоговый проект можно и нужно предложить переделать, доделать, заменить дифференцированным зачетом с оценкой. В любом случае необходимо вместе с учеником тщательно разобраться, что произошло, кто и где допустил ошибку. Ученик ли не понял или педагог не смог объяснить?
Избежать таких последствий можно, если в ходе проектирования проводить проблемные семинары, «открытые» консультации, использовать другие интерактивные виды обучения, насыщая учебную деятельность элементами самостоятельного познания и получения информации.
Для старшеклассников И.Д. Чечель предлагает более сложный рейтинговый подход, где выделены и оцениваются 10 критериев на 4 уровнях (0, 5, 10, 20 баллов). Сложность заключается не в оценке, а в повышенных критериях, приближающихся к вузовским.
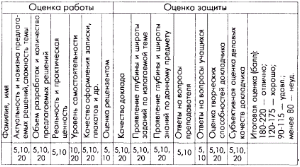
Сама оценка складывается из суммы среднеарифметической величины коллективной оценки, самооценки и оценки преподавателя (естественно, для получения средней величины сумма делится на три). Выделяются 5 критериев выполнения и 5 критериев защиты проекта, и каждый из них оценивается отдельно. Правда, при таком подходе исключена оценка собственно деятельности учащихся в процессе проектирования.
Критерии оценки проектной деятельности
| Критерии оценки | Оценка |
| Актуальность темы |
|
| Реальность проекта |
|
| Оригинальность и разнообразие подходов разработки и реализации проекта |
|
| Раскрытие темы, выполнение поставленных задач |
|
| Качество оформления |
|
| Результат, его анализ, что еще можно сделать? |
|
| Полнота представления работы, наглядность, культура речи, умение отвечать на вопросы, поддерживать интерес к предлагаемой работе. |
|
| Общая оценка |
|
ЗАКЛЮЧЕНИЕ
Организация проектной деятельности должна включать в себя связь с математикой (это будет способствовать поддержанию интереса к предмету, активности изучению материала), реализацию творческого потенциала учащихся, обязательно самостоятельную работу школьников, направленную на приобретение новых знаний и умений
Проектную деятельность целесообразнее осуществлять в три этапа. Первый этап – знакомство с проектной деятельностью,
второй - непосредственная самостоятельная работа над проектом,
третий – анализ проведенной работы, выявление уровня овладения навыками проектной деятельности, определение уровня сформированности «проектных умений».
Необходимо организовать постоянную работу над проектами с целью развития и углубления приобретенных знаний, умений, навыков.
Рассмотрены сущность проектной деятельности и различные точки зрения на определения проекта, метода проектов, изучены положительные аспекты использования метода проектов, возможные трудности, возникающие в ходе организации проектной деятельности.
Выявлен уровень разработанности исследуемого вопроса в методической и педагогической литературе. Определены принципы и требования организации проектной деятельности, цели. Рассмотрены классификации проектов по различным основаниям.
Рассмотрена методика организации проектной деятельности в учебной литературе. В ходе анализа литературы, установлено, что возможность организации проектной деятельности в процессе обучения математике в литературе освещена недостаточно полно.
Разработана и внедрена в процесс обучения математике начальной школы методика организации проектной деятельности . Проведен анализ занятий, выявлены положительные результаты проведенного внедрения. Занятия способствовали формированию познавательной акьтивности , выделенных в дипломной работе.
Задачи исследования решены. Цель работы достигнута.
Для дальнейшего формирования познавательной активности при изучении величин считаю необходимым организацию проектной деятельности в дальнейшем обучении школьников.
В качестве продолжения работы предлагаю рассмотреть возможность установления межпредметных связей учебных предметов в процессе организации проектной деятельности, методику организации проектной деятельности в математике, например, с применением ЭВМ.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Ананченко Н.Ю. Методика преподавания математики. – СПб.: Новая литература, 2010
Антонов Н.С. Современные методики преподавания математики в начальной школе. – СПб.: Новая литература, 2010
Бантова М.А. Методика преподавания математики в начальных классах: .- М.:Просвещение, 2008.
Блон А.А. Методика преподавания математики. – М.: Просвещение, 2008
Берлянд И.Е. Загадки и числа: воображаемые уроки в 1-м классе: – М.: Академия, 2008.
Вернье Ж. Ребенок, математика и реальность: проблемы преподавания математики в начальной школе. – М.: Институт психологии РАН, 2008.
Воропаева Р.Н. Методические советы из опыта преподавания математики начальной школе. – Математика, 2010, № 35
Волкова С.И. Математика и конструирование в 1 классе: – М.: Просвещение, 20088
Волкова С.И. Развитие познавательных способностей детей на уроках математики в 1 классе:– М.: Просвещение, 2008
Волкова С.И. Развитие познавательных способностей детей на уроках математики во 2 классе: – М.: Просвещение, 2009
Груденов Я.И. Психолого-дидактические основы методики обучения математики. – М.: Педагогика, 2008.
Епишева О.Б. Формирование приемов учебной деятельности. – М.: Просвещение, 2008
Еникеева А.М.. Учить школьников учиться математике. – СПб.: Новая литература, , 2010
Ефимова А.И. Проблемы преподавания математики в начальной школе. – СПб.: Новая литература, 2010
Зильберг Н.И. Урок математики в 1-м классе. – М: Наука, 2008
Истомина Н.Б. Активизация учащихся на уроках математики в начальных классах: . – М.: Просвещение, 2008.
Истомина Н.Б. Методика преподавания математики в начальной школе. – М.: Просвещение, 2008
Карп А.П. Даю уроки математики: из опыта работы. - М.: Просвещение, 2008
Корешкова Т.А. Формирование познавательной активности и интереса к математике в школе. – Математика, 2010, № 14
Костицын В.Н. Моделирование на уроках математики: теория и методические рекомендации. – М.: Владос, 2009.
Кошкин Ю.Л. Методика преподавания математики в начальной школе. – М.: Поосвещение, 2009
Лейкина Т.Н. Научиться продумывать!:– СПб.: Питер, 2009
Методика преподавания математики в начальных классах. – М.: Просвещение, 2008.
Моро М.И. Математика в 1-м классе: . – М.: Владос, 2009
Моро М.И. Математика во 2-м классе: – М.: Просвещение, 2008
Моро М.И. Средства обучения математике в начальных классах. – М.: Просвещение, 2009.
Пчелко А.С. Математика в 3 классе: . - М.: Просвещение, 2008.
Пчелко А.С. Основы методики начального обучения математики. М.: Просвещение, 2009
Практикум по методике преподавания математики в средней школе. Под ред. Мишина В.И. – М.: Просвещение, 2008
Рыжик В.И. 25000 уроков математики, 2—е издание. – СПб.: Питер, 2009
Рогоновский Н.М. Методика преподавания математики. – СПб.? Новая литература, 2010
Рохман В.А. Энциклопедия математики. – М.: Наука, 2009
Столяр А.А. Проблемы преподавания математике. – М.: Высшая школа 2010
Уткина Н.Г. Изучение трудных тем по математике в 1 – 3 классах: сборник. – М.: Наука, 2008
Уткина Н.Г. Математическая лаборатория. – М.: Просвещение, 2008
Фрейндентайль Г. Математика как педагогическая задача. – М.: Просвещение, 2008
Тесленко И.Ф. Методика преподавания планиметрии. – М.: Владос, 2009
Чилингирова Л.К. Играя, учимся математике: пособие для учителя. – М.: Владос, 2010.
Шевченко И.Н. Методика обучения математике. – М.: Высшая школа, 2008
Энциклопедический словарь юного математика. – М. Педагогика, 2008
Приложение № 1
Урок математики по теме: "Квадратный сантиметр"
ТЕМА: Площадь фигуры; квадратный сантиметр.
ЦЕЛИ: Ознакомить уч-ся с квадратным сантиметром как единицей, и научить пользоваться этой единицей измерения.
ОБОРУДОВАНИЕ: геометрические фигуры, карточки с заданием, записи на доске, учебник, образец кв.см.
ХОД УРОКА:
Организационный момент.
Индивидуальная работа.
Геометрический материал.
(На наборном полотне выставлены геометрические фигуры).
Круг, прямоугольник, треугольник, квадрат, многоугольник.
Назовите фигуры.
Какое общее название можно дать этим фигурам?
Чем они отличаются?
Что знаете про стороны квадрата?
( У него все стороны равны).
Сообщение новой темы и цели урока.
Сегодня на уроке вы познакомитесь с единицей измерения площади, которая называется квадратный сантиметр и научитесь пользоваться единицей измерения.
(Образец на доске)
Это кв. см.- стороны которого равны 1см.
Он очень маленький, но играет огромную роль в математике.
А сейчас мы научимся чертить кв.см. в тетради.
(Учитель на доске чертит, а дети в тетради).
Повторяю ещё раз:
Это кв.см., при помощи которого мы будем измерять S фигур, короче можно записать так 1 кв.см.
(Учитель подписывает на доске, дети в тетрадях).
ВЫВОД: если в одном кв.см. измеряют S фигур, то в линейных см. измеряют длину отрезка.
Закрепление новой темы.
Начерти фигуру площадью 8 см2.
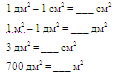
Решение задачи: Площадь одной из комнат трехкомнатной квартиры равна 20 м2, а площадь второй – на 4 м2 меньше. Площадь первых двух комнат на 17 м2 больше площади третьей комнаты. Какова площадь третьей комнаты?
а) Чтение задачи. б) Состав схемы задачи.
(Учитель составляет схему на доске, дети в тетрадях).
в) Решение задачи.
Итог урока.
С какой новой единицей измерения S вы познакомились?
Приложение № 2
Урок математики по теме: "Площадь параллелограмма"
ТЕМА: Площадь параллелограмма.
ЦЕЛИ: Расширить знания учащихся о многоугольниках. Создать ситуацию для нахождения площади параллелограмма. Вывести формулу. Развивать конструктивные навыки и воображение. Воспитывать аккуратность, точность, внимание.
ХОД УРОКА:
Закрепление. Подготовка материала для будущей работы.
Устный счет.
На конверт наклеили марку, длиной 26 мм. Какую площадь она занимает на конверте?
Чем занимаемся на уроках математики? (Находим площади фигур). Хорошо умеете находить площадь? (Да).
Найдите площади фигур.
Умеете находить S?
По какой формуле нашли первую площадь S 1? ( S = а х в: 2)
По какой формуле нашли вторую площадь S 2? (S = а х h: 2)
Что такое h?
2. Актуализация.
Молодцы! А теперь найдите площадь этой фигуры.
Смогли выполнить задание?
Что вас удивило?
Чем это задание не похоже на предыдущее? (Это не треугольник).
3. Постановка проблемы и формулирование темы урока.
Какой возникает вопрос? (Как найти площадь новой фигуры)
Сообщаю детям, что новая фигура называется параллелограмм, вывешиваю карточку с новым термином.
Какая тема урока? (Как найти площадь параллелограмма?)
4. Поиск решения.
Какие у вас есть гипотезы?
Обсудите в группе план решения задачи (оформляют решение на листе).
Представление группами работ, коллективное обсуждение, поиск правильного решения.
Как искали площадь параллелограмма? (Использовали способ перекроя).
Запись в тетради:
а = 8 см
h = 6 см
8 х 6 = 48 (см 2)
Ответ: 48 см 2
Кто может записать формулу для нахождения параллелограмма? (S = a х h)
5. Закрепление.
Найдите площадь, если а = 17 см, h = 8 см.
6. Итог работы.
Что узнали на уроке?
Кто может рассказать, как найти площадь параллелограмма?
Оцените на шкале, как вы поработали сегодня на уроке.
Приложение № 3
Урок математики по теме: "Единица измерения площади. Квадратный метр"
ТЕМА: Единица измерения площади. Квадратный метр.
ЦЕЛИ: Дать предоставление о квадратном метре; закрепить умение учащихся находить площади различных фигур (многоугольник); воспитывать чувство взаимоподдержки и выручки; продолжить работу над формированием вычислительных навыков; развивать логическое мышление.
ОБОРУДОВАНИЕ: карточки с геометрическими фигурами на парте; карточки с монетами на парте; волшебные квадратные очки, картинки фруктов; шагомер или ватерпас, рулетка, складной метр, задачники Г. Остера, его книги; задачник, тетради, линейки, простой карандаш.
ХОД УРОКА:
Если к нам приходят гости Не здоровайся ни с кем. Отвернись и на вопросы Ни на чьи не отвечай.
Хороший совет я вам дала? Как называются такие советы? А чтобы совет стал хорошим, что нужно сделать? Сделайте наоборот.
Кто сочинил такие вредные советы? (Г. Остер). Какие произведения Г. Остера вы прочитали и вам понравились? (Выставка книг).
Но у нас сейчас урок математики, и чем может быть интересен Г. Остер? Нынче этому задачнику исполняется 10 лет. Он даже старше вас. А чтобы нам работать с этим учебником, нужно вооружиться карандашом и надеть наши волшебные очки. Что вы можете сказать о них? (Если мы посмотрим через них, все должно казаться квадратным).
Рисунок 1
Открываю доску, показываю яблоко, грушу, банан.
Рисунок 2
Какой формы будет вот то яблоко? Это груша? Это банан? Почему? Докажите.
А сейчас у вас на столах лежат листочки с фигурами квадратной формы.
Рисунок 3
Кто это может быть? Хотите дорисовать? Мне тоже интересно узнать, что же у вас получится. (Отметить разных животных. Вот какие разные у нас получились животные).
А какое задание можно предложить по этим фигурам? Что можно определить? (Определить S).
Определите разными способами (3 х 3 = 9 см2, 4 х 5 = 20, 9 +20 = 29 см2). Какой способ самый рациональный? Почему?
Работа с задачником.
Теперь вы вооружились. У вас есть палетки и волшебные очки. Давайте посмотрим, что же нам предлагает Г. Остер? Откройте задачу с красной закладкой на странице 39 № 88. Прочитайте внимательно текст 88.
Длина стороны зеркала квадратной формы 10 дм. Скольким квадратным метрам будет равна площадь отражения лица царевны Несмеяны, если, когда она любуется собой, это отражение занимает как раз всю площадь зеркала?
О чем эта задача? Объясни свой ответ. Понравился вам вопрос задачи? Можно ли сократить вопрос?
Давайте уберем лишние слова. Какой вопрос тогда получится? А достаточно ли данных? (Да). Почему? (У квадрата все стороны равны). Что можно сказать о другой длине?
Прочтите еще раз вопрос задачи. В вопросе есть слова (на доске пишу слова – Квадратный метр). Квадратный метр. Найдите корень слова.
Вот квадрат. Похоже на форму зеркала Царевны-Несмеяны? (Показываю полиэтиленовую пленку размером 1м х 1м).
Что сказано в задаче о длине сторон квадратного зеркала? (10 дм – это что? 1 м). Есть у нас такая мерка, которая поможет найти площадь этого зеркала? Как это сделать? Выложим. Сколько квадратных дециметров мы выложили? 100 дм2 = 1 м2. А как узнаем? 10 х 10 = 100. Вот у нас получилась новая мера площади – 1 м2.
Вот такое лицо было у Царевны-Несмеяны. А может быть, такое лицо у человека?
Рисунок 4
Какой литературный прием использовал Г. Остер в своей задаче? (Преувеличение). Лицо большое, как будто смотрится в увеличительное стекло.
А сейчас откройте последнюю страницу тетради, где наш справочник. Какие единицы измерения площади у нас записаны? Давайте запишем в наш справочник новую единицу измерения площади – 1 м2 = 100 дм2. У нас уже есть мерка, это палетка – 1 дм2. Сегодня новая мерка 1 м2.
А следующая задача еще интереснее. Откройте задачу с зеленой закладкой. Прочитайте.
На кухне площадью 6 кв.м. дедушка рассыпал мелочь. С каждого квадратного метра бабушка собрала по 45 копеек. Каков общий урожай?
Какие данные нам известны? S – 6 м2, 1м2 – по 45 к.
Что мы должны найти? Что это означает? Вот наши квадратные метры. Какой формы может быть кухня. Давайте выложим. А по-другому как можно переставить? Сколько возможных вариантов может быть?
Давайте в тетради нарисуем возможные варианты. Ребята, 1 м2 войдет в тетрадь? Нет. Значит, что нужно сделать? Было преувеличение, а теперь нужно уменьшить до 1 клетки. Кто сколько вариантов найдет?
Рисунок 6
Проверка и показ нескольких работ.
У кого другая форма? Вот какие формы могли быть у кухни. А теперь разберемся с мебелью. Что в задаче сказано про копейки? С каждого метра по 45 коп. Какие сейчас у нас копейки есть? 1, 5, 10, 50. Есть еще другие. 50 копеек нам понадобится? Нет. Значит отбрасываем. Какой набор копеек могла собрать бабушка с каждого метра?
Я сейчас раздам вам задание, а вы подумайте, какими копейками можно собрать 45 к.
Рисунок 7
Работаем в паре. Кто закончит, поднимите руку. Покажите, как вы набрали. Выложите 1 м2 на полу. А теперь мы можем подсчитать, каков общий урожай монет. Найдите результат наиболее рациональным, удобным способом. Решение запишите в тетради.
Вызвать к доске учащихся, у которых разные варианты.
45 х 6 = 270 к, 45 + 45 + 45 + 45 + 45 + 45 = 270
Как вы думаете, трудно было бабушке собрать столько мелочи?
Ну, как вам понравились задачки Г. Остера? Какой литературный прием он любит применять?
А сами смогли бы придумать такие задачки? Вот домашнее задание. Подумайте, постарайтесь придумать для соседа такие задачки на листочке (А4) с рисунком. Написать условие. Тогда у нас завтра получится свой классный задачник.
Вот теперь вы знаете, что чем можно измерять, и можете помочь своими родным измерять площади.
Урок окончен.
52

 Получите свидетельство
Получите свидетельство Вход
Вход






















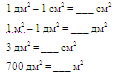









 Проектная деятельность при изучении величин в курсе математики (0.39 MB)
Проектная деятельность при изучении величин в курсе математики (0.39 MB)
 1
1 5101
5101 138
138 Нравится
0
Нравится
0


