КГУ «Литвинская школа-интернат для детей-сирот и детей, оставшихся без попечения родителей»
Составление исследовательских задач по математике для учащихся 5-6 классов.
Проект.
Учитель: Тимофеева С.А.
Целью решения задач является развитие
математического мышления и выработка
начального этапа творческой исследовательской
работы.
В.М.Брадис
Смена парадигм образования затронула не только цели и задачи, стоящие перед общеобразовательной школой, но и организацию деятельности учителя, разносторонность учебно-познавательной деятельности учащихся, а также и такой компонент педагогического процесса, как задания, предлагаемые учащимся. В современных условиях поиск путей изменения целей, форм, методов, объема заданий по математике ориентируется на обучаемого, строится с учетом интересов, склонностей, возможностей ученика. Несмотря на достаточный резерв дидактических возможностей математических заданий из учебника, реализация учителями этого потенциала в практической деятельности осуществляется порой недостаточно. Между тем такой вид заданий, как исследовательские, имеет большие возможности в достижении цели развития качеств личности и субъективных черт ребенка.
Сейчас, когда предметно-ориентированная парадигма образования сменяется на личностно-ориентированную, следует определить роль учащегося, его главную задачу не только в получении знаний о существующих в окружающем мире и описываемых математическими моделями зависимостях, но и в овладении методологией творческого поиска. Заметим, что изучение математики в массовой школе осуществляется традиционно и, несмотря на использование элементов дифференцированного и вариативного обучения, приспособлено в основном для обучения учащихся фактам, а не для процесса получения фактов, тогда как C. Рубинштейн отмечал, что «процесс накопления знаний и умений называется учением, а процесс приобретения способностей - развитием» [137, с. 221].
Результаты проведенного анкетирования учителей математики общеобразовательных школ показывают, что большинство педагогов считают необходимым систематическое вовлечение учащихся в учебные исследования при изучении математики, но испытывают трудности, связанные с отсутствием соответствующего методического обеспечения. Кроме того, исследовательская, работа обычно занимает много учебного времени и напрямую не связана с усвоением изучаемого материала, поэтому в теории методики обучения она рассматривается в рамках исследовательского метода, а в практике обучения математике исследовательская работа проводится эпизодически и спонтанно.
Таким образом, в настоящее время имеют место противоречия:
- между концептуальной установкой на развитие учащихся с помощью средств математики (образование с помощью математики) и существующими пробелами в разработке методического обеспечения обучения математике в условиях новой парадигмы образования;
- между возможностями исследовательских заданий, способствующих развитию творческой самостоятельности учащихся, и складывающейся практикой их применения в условиях отсутствия разработанной методики реализации учебных исследований при обучении математике в 5-6 классах.
Сформулированные противоречия обусловливают актуальность данного проекта и определяют проблему, состоящую в разрешении противоречия между существующим методическим подходом к обучению математике, при котором акцент сделан на обучающие функции, и необходимостью такой организации процесса обучения математике, при которой акцент был бы сделан на развивающие функции заданий, предлагаемых учащимся.
Цель исследования: обоснование процессов проектирования и реализации методики обучения проведению учебных исследований по математике, способствующих развитию творческой самостоятельности учащихся 5-6 классов.
Объект исследования: процесс обучения математике в 5-6 классах общеобразовательной школы.
Предмет исследования: учебные исследования по математике как средство развития творческой самостоятельности учащихся 5-6 классов.
Гипотеза исследования: если в систему работы по математике в 5-6 классах целенаправленно и систематично включать задания, выполнение которых предполагает проведение учебных исследований, то это позволит повысить степень обученности учащихся и развить их творческую самостоятельность, будет способствовать развитию у учащихся мыслительных процессов, в том числе творческого мышления.
Для реализации поставленной цели в свете выявленной проблемы исследования потребовалось решить следующие задачи:
1. Выявить сущность понятия «исследовательское задание» и обосновать его роль в условиях смены парадигм образования.
2. Выявить роль и место учебных исследований в процессе обучения математике учащихся 5-6 классов.
3. Разработать методику обучения учащихся решению поисково-исследовательских задач и рекомендации для учителя по составлению таких задач.
4. Определить основные формы учебной работы при обучении учащихся решению поисково-исследовательские задачи, направленных на развитие творческого мышления.
5.Отобрать и составить поисково-исследовательские задачи для построения содержательно-методической линии этих задач.
Глава 1. Исследовательские задачи: теория, методика составления и их роль в развитии исследовательских навыков у учащихся.
Исследовательские задачи
Исследовательскую деятельность следует рассматривать как особый вид интеллектуально-творческой деятельности, порождаемый в результате функционирования механизмов поисковой активности и строящийся на базе исследовательского поведения. Успешное осуществление исследовательской деятельности требует наличия у субъекта специфического личностного образования – исследовательских способностей. Под способами и приемами исследовательской деятельности следует понимать способы и приемы, необходимые при осуществлении исследовательской деятельности. Это умение видеть проблемы, умение вырабатывать гипотезы, умение наблюдать, умение проводить эксперименты, умение давать определения понятиям и др.
Сегодня важно учить детей использовать свой опыт, знания, умения и качества личности для решения конкретных проблем, формировать научную картину мира, научить находить путь от научного описания к способностям ориентироваться в конкретных явлениях. Главная проблема школы – это переход от информативного метода обучения к активной творческой деятельности всего педагогического сообщества, т.е. педагогического коллектива, учащихся и родителей.
Один из компонентов исследовательской деятельности – исследовательские умения, которые определяются как система интеллектуальных, практических умений и навыков учебного труда, необходимого для самостоятельного исследования или его части. Для их формирования можно решать учебно-исследовательские задачи (задачи, процесс решения которых требует выполнения одного или нескольких исследовательских умений), используя традиционные технологии в сочетании с информационными, уделяя последним больше внимания, когда они имеют преимущества.
Учебная исследовательская деятельность определяется как деятельность учащихся по исследованию различных объектов с соблюдением процедур и этапов, близких научному исследованию, но адаптированных к уровню познавательных возможностей учащихся.
Учебная исследовательская деятельность – это специально организованная учебная деятельность под руководством педагога, направленная на исследование различных объектов с соблюдением процедур и этапов, близких научному исследованию, но адаптированных к уровню познавательных возможностей школьников
Таким образом, можно выделить два подхода к обучению. При одном – назовем его традиционным – ученик изучает новую теорию, решает задачу, получает оценку и ждёт от учителя новой задачи. Предполагается, что у задачи есть единственный правильный ответ и учитель его знает. При другом подходе – назовём его исследовательским – ученик сам ставит вопросы и ищет на них ответы, выдвигает гипотезы, доказывает и опровергает их. Всякий полученный ответ может стать основанием для новых вопросов. Результат может быть не известен учителю заранее. Можно сказать, что ученик попадает в новый математический мир и учится жить в нем.
Существует несколько мнений об исследовательских задачах:
«Они доступны только старшеклассникам» 25% опрошенных
«Они нужны только сильным школьникам» 18 % опрошенных
«Учёба отдельно, исследования отдельно» 18 % опрошенных
«Исследовательские задачи доступны учащимся 5-6 классов» 39 % опрошенных
Подавляющее большинство учителей все-таки придерживаются мнения, что для того, чтобы начинать решать такие задачи, не надо ждать старших классов, уже материал 5-6 классов позволяет вводить элементы исследования. Полезно начинать с самого простого, с вещей, доступных несильным ученикам. Далее, хорошее обучение должно дать понятие о методах, характерных для изучаемой науки. При работе с исследовательскими задачами ученикам неизбежно приходится иметь дело с методами науки математики, поэтому исследовательские задачи могут стать органической частью обучения математике и существует объективная возможность для начала формирования общих исследовательских умений на самых ранних стадиях обучения, а именно в 5-6 классах, и даже в начальной школе. Закладка основных содержательных линий математического образования, включающего в себя, в том числе, и общие исследовательские умения, происходит на начальном этапе обучения. Уже на нем возможно формирование интеллектуальных навыков высокого уровня, способствующих выработке научного стиля мышления, творческому развитию личности. Научный стиль мышления и присущие ему исследовательские качества формируются в процессе активной познавательной деятельности, одним из компонентов которой является учебно-исследовательская. Уже на начальном этапе изучения математики возможно использование элементов учебных математических исследований, организованных как задачи определенного вида.Для активизации познавательной деятельности и развития математического мышления в 5-6 классах детям должны предлагаться задачи разных видов. Среди них выделяются поисковые задачи, результатом решения которых, как правило, является догадка, т.е. нахождение пути (способа) решения. Появление догадки свидетельствует о развитии у учащихся таких качеств умственной деятельности, как смекалка и сообразительность. Смекалка определяется в педагогике как особый вид проявления творчества в нахождении способа решения. Она проявляется в результате анализа, сравнений, обобщений, установления связей, аналогий, выводов, умозаключений. Большая роль отводится интуиции обучаемого.О проявлении сообразительности свидетельствует умение обдумывать конкретную ситуацию, устанавливать взаимосвязи, на основе которых ученик самостоятельно приходит к выводам, обобщениям, оперируя знаниями. Наиболее полно такие приемы умственной деятельности, как сравнение, обобщение, абстрагирование проявляются при решении задач следующих видов: задачи на нахождение общего признака изображенных предметов, нахождение отличий между ними, на продолжение числового ряда или ряда фигур, поиск недостающей в ряду фигуры, нахождение признака отличия одной группы фигур от другой. Для решения таких задач ученик должен уметь проводить последовательный анализ фигур обеих групп с выделением и обобщением признаков, свойственных каждой из них. Помимо этих, учащимся могут быть предложены задачи на составление орнаментов, игровые задания с использованием геометрического конструктора, логические задачи. Так, например, А.В.Хуторской [8] рассматривает элементы математических исследований учащимися начальной школы в виде составления собственных числовых рядов, числовых таблиц, выявления связей чисел и геометрических фигур, обнаружения математических закономерностей в окружающих явлениях и календарях, придумывания и применения собственных мер измерения.
Типы исследовательских задач.
Произведем следующее условное разделение заданий, предлагаемых в учебнике математики на два типа, взаимно дополняющих друг друга. В некоторых случаях они могут быть объединены в общее задание.
1 тип - стандартные задачи, обеспечивающие деятельность учащихся по образцу или изученному правилу (выполнение вычислений, измерений, практических заданий и т.п.)
П тип - задачи, обеспечивающие деятельность по выработке интеллектуальных навыков, включающих в себя ряд исследовательских умений:
а) умение проводить анализ наблюдаемых объектов и выполнять описание наблюдений;
б) умение классифицировать объекты (выделять существенные признаки объекта или последовательности объектов, устанавливать основание классификации или делать выбор основания);
в) умение обобщать и находить закономерности;
г) умение конструировать математические объекты.
Наличие задач второго типа в учебниках по математике 5-6 классов способствует формированию научного стиля мышления, что соответствует основным положениям концепции развивающего обучения, обеспечивают пропедевтику формирования исследовательских умений в ходе обучения математике в 7-11 классах .
Характеризуя принципы организации задачного материала в этом учебном комплекте, обратим внимание на задания, с помощью которых вводятся новые понятия. Большей частью новые понятия формируются в процессе поиска ответа к поставленной задаче на основе наблюдения вводимых новых объектов и описания наблюдаемых свойств, их первоначального анализа. Роль наблюдений существенна при принятии решения о выборе метода решения задачи, она тесно связана с математической интуицией обучающихся и зависима от наглядности предъявляемых объектов. С помощью наблюдений над результатами выполняемых действий учащиеся подводятся к усвоению приемов поиска закономерностей в числовых последовательностях. На этой связи построены двухкомпонентные задания, одной из частей которых служит алгоритмическое задание, а второй частью - исследовательское по обнаружению характера зависимости между величинами.
Примером таких заданий может служить задание:
Пример 1. Увеличивай дробь 0,6 в 10 раз, в 100 раз, в 1000 раз. Наблюдай, что будет изменяться. Сделай вывод».
Большое значение для последующего интеллектуального формирования личности имеют задачи на выделение существенных признаков объекта, поиск сходства и отличия нескольких объектов. Тем самым осуществляется пропедевтика умений классифицировать объекты по выбранному основанию . Для составления таких задач авторы привлекают как арифметические, так и геометрические объекты.
Пример 2. . По какому признаку числа 12,17,18,16,45,98,21,20,45 разбили на две группы? Учащиеся могут выделить следующие признаки: по четности и нечетности последней цифры.
Не менее важны и задачи, формирующие умения обобщать факты, обнаруживать общие правила, т.е. подводящие к задачам на формирование обобщенного способа действий.
Пример 3. «Разгадай правило, по которому записан каждый ряд чисел, и продолжи его:
а) 123, 246, 492, 984, …
б) 15, 75, 375, 1875,…
в) 3020 , 3220, 3420, 3620,… »
Пример 4. « Какую закономерность ты заметил в построении ряда чисел: 3545, 3550, 3555, 3560, 3565,… ? Продолжи ряд по тому же правилу. Можно ли утверждать, что каждое число этого ряда делится на 5 ?»
К задачам, формирующим исследовательские умения, мы отнесли и задания на конструирование математических объектов: новых фигур, уравнений, неравенств, сюжетных задач, схем к сюжетным задачам.
Пример 5. «Придумай выражения, в которых уменьшаемое равно 9, и найди их значения».
Пример 6. « В одном альбоме 48 марок, в другом 37. Поставь вопросы к данному условию. Запиши решение каждой задачи выражением. Вычисли значения этих выражений».
Пример 7. «Составь верные равенства на деление, в которых:
а) делитель - двузначное число, а значение частного - трехзначное число;
б) делитель - однозначное число, значение частного - трехзначное число;
в)делитель- трехзначное число, значение частного - однозначное число».
Соотношение задач исследовательского характера, предложенных в учебнике, очень даже невелико, поэтому возникает необходимость проектирования системы таких заданий самим учителем.
Проектирование заданий исследовательского характера
При составлении исследовательской задачи должны соблюдаться определенные правила:
*Содержание задачи должно учитывать разнообразные интересы учащихся, охватывать объем учебной темы или иметь интегрированный характер (внутрипредметный, межпредметный).
* Задача должна иметь уровневый характер, и ее выполнение подразумевать технологическую готовность школьника.
* Качественная задача должна содержать противоречие, иметь достаточное условие для его решения.
* В тексте задачи, исходя из необходимости, может быть указана литература, которая обязательно должна быть в наличии в рабочем кабинете или в библиотеке школы, а также даны ссылки на возможность использования помощи при возникновении затруднений в его выполнении;
* Задача должна предусматривать различные формы работы, в том числе сотрудничество с другими участниками поиска.
* Время выполнения задачи может быть различно из-за сложности, объема, содержания, условий выполнения (на уроке, дома).
* В комментариях к задаче должны быть предусмотрены этапы рефлексии (осознания поиска).
* Выполнение задания может происходить с использованием не только теоретических, но и экспериментальных методов исследования.
* Задача может иметь неполное условие в случае, если имеется доступ в процессе его решения к носителям информации в электронном и печатном виде.
* Задача может иметь многовариантное решение.
В основу проектирования системы учебных исследований должны быть положены принципы системного подхода. Проектирование системы учебных исследований проведено в соответствии с такими этапами:
1) целеполагание и выявление логической структуры учебного исследования с учетом разработанной классификации исследований;
2) отбор средств и методов, используемых при организации учебных исследований;
3) разработка содержания дифференцированных заданий для учебных исследований, соответствующих уровню развития творческой самостоятельности учащихся;
4) определение форм учебной деятельности и дозирования помощи учащимся при самостоятельном решении исследовательских заданий;
5) итоговый анализ (рефлексия).
Спроектированная система домашних учебных исследований, должна быть направлена на развитие творческой самостоятельности и отвечать следующим требованиям:
• система учебных исследований построена с учетом принципа целостности, т. е. обладает свойством структурной полноты;
• каждый компонент системы соответствует конкретной дидактической цели формирования определенного приема учебной деятельности;
• система учебных исследований направлена на развитие творческой самостоятельности учащихся, способствует формированию исследовательских умений и обеспечивает постепенное возрастание уровня развития самостоятельности учащихся;
• учебные исследования соответствуют содержанию программного материала и учебным возможностям школьников;
• задания приводятся по нарастающей степени трудности;
• содержание учебных исследований имеет положительную мотивацию.
В процессе реализации этих положений нами были выделены три вида исследовательских заданий по математике, отличающиеся друг от друга присутствием в решении исследовательских компонентов, продолжительностью выполнения и числом учащихся, вовлеченных в решение задания, названные нами условно «урок-исследование», «мини-исследование» и «исследовательский комплекс». Основное назначение этой классификация - выбор оптимального для конкретной ситуации варианта включения исследовательских заданий в процесс обучения, а также демонстрация различных приемов составления исследовательских заданий.
Включение исследовательских заданий в процесс обучения происходит с учетом стимулов возникновения и развития познавательного интереса к математике. При этом способы организации познавательной деятельности учащихся, играющие основную роль в воспитании познавательного интереса, усиливаются стимулами, связанными с содержанием изучаемого материала и с отношениями между участниками учебного процесса.
Основные виды задач:
Логическая цепочка связанных между собою задач, построенная на основе ключевой задачи учебной программы.
Учебно-исследовательские задачи, организованные по принципу пучка задач, связанных общностью идеи решения, которую и должны самостоятельно выдвинуть ученики.
Многокомпонентное задание, созданное на основе ключевой задачи, в котором главной является обобщенная задача.
Учебно-исследовательская задача аналог опорной. Целью постановки является формирование умений поиска сходства и отличия.
Многокомпонентные задачи межпредметного характера.
Самостоятельно составленная учащимся новая задача по изученному материалу.
На основе этой типологии учебно-исследовательских математических задач приведем виды конструирования задач по этой классификации:
Подготовительные (пропедевтические) задачи для средних классов (5-7). В основном это задачи на формирование обобщенного способа действий, на смекалку, сюжетные, задачи на конструирование математических объектов.
Можно составить и следующие задачи: 1) Исключите лишнюю фигуру {по приведенным геометрическим фигурам).
Исключите лишнее число: 2, 12, 17,23.,
Творческое задание: Составить самостоятельно задачи на исключение лишнего. Чем большим числом способов решаются задачи, тем лучше.
Логическая цепочка связанных мезду собой задач, построенная на основе ключевой задачи.
Рассмотрим исследовательскую задачу.
Задание. Исследовать некоторые свойства произведения двух последовательных натуральных чисел и составить задачи, основанные на этих свойствах.
В результате ученики могут составить такие задачи.
Доказать, что ни при каком натуральном п число вида п2 + п +1 не делится на 5.
Доказать, что при любой перестановке цифр в числе 54178931 не получится числа, являющегося произведением двух последовательных натуральных чисел.
В данном возрасте также работа над литературой, а именно, самостоятельное изучение какой-либо темы, способствует формированию у учащихся умений и навыков исследовательской деятельности. В этом возрасте можно применить следующие виды исследовательской деятельности:1. проблемное видение и постановка проблемы;2. построение и выдвижение гипотез;3. творческая переработка и применение знаний. Необходимо подбирать задания таким образом, чтобы процесс решения способствовал возрастанию творческой активности, познавательного интереса к математике и смежным предметам, позволял повысить творческий характер учебного процесса.
К числу заданий исследовательского характера могут быть отнесены:
- фокусы с разгадыванием задуманных чисел, со скоростным сложением трех или пяти многозначных чисел, со скоростным умножением или делением некоторых чисел;
- задания с занимательными рамками и магическими квадратами;
- софизмы (например, доказательство того, что 2 + 2 = 5);
- игры типа "Кто первым получит 50" и т.п.
Исследовательский характер этих заданий относится к разгадыванию способа выполнения фокуса или к выработке выигрышной стратегии игры.
Фокусы с разгадыванием задуманных чисел могут быть разного уровня сложности, который в основном определяется числами, набором и количеством выполняемых над ними действий. Простейшие фокусы включают 2–3 действия сложения и вычитания над числами в пределах 10, затем 20. Достаточно сложные фокусы предполагают действия с многозначными числами, например, одновременное сложение большого количества чисел или последовательное выполнение 5–6 разнородных действий. В одном фокусе может быть разгадано сразу несколько чисел, например, чей-то день, месяц и год рождения. Приведем примеры фокусов разного уровня сложности.
Фокус 1. Задумайте число, прибавьте к нему 14, к результату прибавьте 6, вычтите задуманное число. У вас получилось 20.
Формула для разгадывания фокуса:
а + 14 + 6 – а = 20. Ее можно проиллюстрировать на схематическом чертеже. Для обоснования можно воспользоваться доступными ученикам знаниями – сочетательным свойством сложения: а + 14 + 6 = = а + (14 + 6) =
= а + 20; а также взаимосвязью суммы и слагаемых: а + 20 – а = 20 (из суммы а + 20 вычли слагаемое а, получили другое слагаемое 20).
Фокус 2. (старинный фокус из главы "Об утешных неких действиях, через арифметику употребляемых" учебника "Арифметика" Л.Ф. Магницкого) состоит в угадывании, у кого из восьми человек (n1), на каком пальце (n2), на каком суставе (n3) находится перстень. Загадывающий умножает на 2 номер человека, прибавляет 5, умножает результат на 5, прибавляет номер пальца, умножает результат на 10, прибавляет номер сустава и сообщает полученное число тому, кто отгадывает. Пусть перстень находится у четвертого человека (n1 = 4), надет на пятый палец (n2 = 5), на второй сустав (n3 = 5). Выполнив вычисления, приведенные в таблице, можно отгадать, у кого находится перстень.
| n1-2 | +5 | -5 | +n2 | -10 | +n3 |
| 4-2=8 | 8+5=13 | 13-5=65 | 65+5=70 | 70-10=700 | 700+2 |
Если из результата (у нас число 702) вычесть 250, то в ответе (452) первая цифра обозначает номер человека, вторая – номер пальца, третья – номер сустава.
Формула для разгадывания в общем случае выглядит так:
((n1 ∙ 2 + 5) ∙ 5 + n2) ∙ 10 + n3 = n1 ∙ 100 + n2 ∙ 10 + n3 + 250, в нашем случае: ((4 ∙ 2 + 5) ∙ 5 + 5) ∙ 10 + 2 = 400 + 50 + 2 + 250.
Разгадывание этого фокуса, описанного Л.Ф. Магницким более трехсот лет назад (1703), вызывает у младших школьников интерес и своим содержанием, и происхождением.
Фокус 3. (фокус с числом Шехерезады). Участвуют пять человек. Первый участник задумывает трехзначное число и записывает его на бумаге. Второй приписывает к нему-то же самое трехзначное число. Третий делит шестизначное число на 7. Четвертый делит то, что получилось, на 11. Пятый делит то, что получилось, на 13 и передает ведущему. Ведущий отдает результат первому участнику, который видит задуманное им трехзначное число. (Последовательность деления шестизначного числа на 7, 11, 13 может быть произвольной.) Пусть задумано число 583; после приписывания его же получаем 583583. Выполняем деление: 583583: 7 = 83369, 83369: 11 = 7579, 7579: 13 = 583 – задуманное число. Разгадка фокуса основана на:
а) том, что для нахождения результата умножения трехзначного числа на 1001 (число Шехерезады) достаточно это трехзначное число записать дважды, например:462 ∙ 1 001= 462462;
б) том, что произведение чисел 7, 11, 13 равно 1001;
в) свойстве деления числа на произведение: abcabc: 7: 11: 13 =
= abcabc: (7 ∙ 11 ∙ 13) = abc.
Участие в фокусе не обеспечивает исследовательской деятельности школьника, он решает исследовательскую задачу только при разгадывании его сути. После чего он сам может показать фокус другим. Эта перспектива стимулирует его активную деятельность. Однако, прежде чем приступить к разгадыванию фокуса, целесообразно несколько раз проверить его с разными числами. В этом случае ученики закрепляют свои вычислительные умения, не испытывая усталости (как при решении обычного столбика примеров), поскольку они заинтересованы в результате.
Исследовательский характер некоторых игр тоже кроется не в процессе игры (играть можно, просто выполняя вычисления в соответствии с правилами), а в поиске способа выигрыша. Например, в игре "Кто первый получит 50?" участвуют два человека. Первый может назвать любое целое число от 1 до 5. Второй прибавляет к нему свое число в тех же пределах и т.д. (каждый игрок прибавляет свое число к предыдущей сумме). Выиграет тот, кто первым получит сумму 50.
Для того чтобы победить, надо решить исследовательскую задачу по выработке стратегии игры. Надо подумать, какое число должен назвать победитель в свой предпоследний ход. Если он назовет 45 (46, 47, 48, 49), то его противник прибавит 5 (4, 3, 2, 1) и выиграет. Если он назовет меньше, например 43 (или 42), то противник может прибавить 1, тогда получится 44 (43), т.е. до 50 будет не хватать 6 (7). Эту разницу за один ход не преодолеть, так как нельзя прибавить больше 5. Значит, победа будет отдана противнику. Тот, кто в свой предпоследний ход назовет результат на 5 + 1 меньше, чем 50, т.е. число 44, тот и выиграет. Какое бы число от 1 до 5 ни назвал затем второй игрок, первый может дополнить его число до 6 и получить 50. Рассуждая так же и вычитая из числа 44 по 6, получим ключевые суммы 38, 32, 26, 20, 14, 8. Их получение обеспечит победу первому игроку, если он начал игру с числа 2.
Эту игру можно варьировать, изменяя "шаг" (число, которое прибавляют за один ход) и конечную сумму. Подчеркнем, что ее исследовательский характер проявляется в процессе разработки стратегии выигрыша.
Особый интерес представляют игры, исследовательская суть которых проявляется во время их проведения. Например, суть игры с номерами билетов состоит в том, что из цифр билета для проезда на транспорте надо получить число 100, используя арифметические действия и скобки. Любые две (и даже три) соседние цифры при желании можно рассматривать как одно число. Если с одним номером играет несколько человек, то выигрывает тот, кто находит больше вариантов (время можно ограничить). Так, имея билет с номером 114455, можно составить несколько выражений со значением 100:
1) 1: 1 + 44 + 55 = 100;
2) 1 + 1 ∙ 44 + 55 = 100;
3) 114 – (4 + 5 + 5) = 100;
4) (1 + 1 + 4 + 4) ∙ (5 + 5) = 10 ∙ 10 = 100;
5) (11 – 4: 4) ∙ (5 + 5) = 10 ∙ 10 = 100;
6) (1 – 1) ∙ 4 + 4 ∙ 5 ∙ 5 = 4 ∙ 5 ∙ 5 = 100.
Подбор вариантов может происходить по-разному. Сначала целесообразно предоставить учащимся возможность осуществить поиск самостоятельно, хаотично. Потом его можно частично упорядочить, взяв за основу определенное арифметическое действие (чаще сложение или умножение, реже вычитание). При этом в записи имеющихся шести цифр можно увидеть ключевое, как правило, двузначное, число, к которому подбирают остальные слагаемые или множители (комбинация остальных цифр должна дополнить имеющееся число до 100). Например, в вариантах 1 и 2 основу суммы составляют сразу два числа – 44 и 55. Варианты отличаются тем, что в первом случае из двух оставшихся единиц получили 1 (это можно было сделать умножением или делением), а во втором – одну из единиц использовали в качестве нейтрального элемента в произведении. В основе варианта 3 лежит вычитание из числа 114 "лишних" 14 единиц. Остальные варианты получены на основе умножения: 100 = 10 ∙ 10 (варианты 4, 5), 100 = 4 ∙ 5 ∙ 5 (вариант 6). В варианте 6 первые три цифры оказались лишними, их можно убрать за счет умножения или деления нуля, полученного вычитанием одинаковых чисел. На множестве целых чисел могут быть еще другие варианты, например:
(– 1 • 1 + 4 ∙ 4 + 5) ∙ 5 = 20 ∙ 5 = 100;
(– 1 – 1 + 4) ∙ (45 + 5) = 2 ∙ 50 = 100.
Постепенно поиск усложняется тем, что слагаемые получают умножением и делением как однозначных, так и двузначных чисел.
В данной игре развиваются такие качества творческого мышления, как вариативность (способность находить несколько способов решения теоретических и практических задач при отсутствии специальных указаний на это и выбирать из них оптимальный); гибкость (способность легко переходить от явлений одного класса к явлениям другого класса, часто далеким по содержанию); оригинальность (способность выдвигать новые, неожиданные идеи, отличающиеся от широко известных, общепринятых).
Эта игра также развивает общие умственные действия (анализ, сравнение, обобщение), умение устанавливать причинно-следственные связи. Кроме того, она способствует более глубокому проникновению в процесс вычислений, формированию "чувства числа", усвоению правила порядка выполнения действий, формированию вычислительных умений.
Известно, что для развития личности важно, чтобы в основе ее творческой деятельности лежали мотивы, непосредственно связанные с содержанием деятельности. Во время описанной выше игры есть возможность увлечь младших школьников процессом поиска разных вариантов. Играть с номером билета можно одному, с друзьями или родителями в транспорте, в школе, дома. Многолетний опыт использования этой игры показывает, что ребенка (и взрослого) увлекает сам процесс, радует каждый найденный вариант вычисления. Положительные эмоции от интеллектуальной работы – важный фактор приобщения к культуре. Для того чтобы подготовить детей к игре, можно использовать знакомое задание:
"Расставьте скобки так, чтобы равенства стали верными:
120 – 90: 15 ∙ 2 + 1 = 5;
120 – 90: 15 ∙ 2 + 1 = 118;
120 – 90: 15 ∙ 2 + 1 = 112;
120 – 90: 15 ∙ 2 + 1 = 107;
120 – 90: 15 ∙ 2 + 1 = 2;
120 – 90: 15 ∙ 2 + 1 = 6;
120 – 90: 15 ∙ 2 + 1 = 229".
Это упражнение проще описанной выше игры тем, что в нем уже зафиксированы числа и арифметические действия.
Занимательные здания исследовательского характера развивают учащихся в перечисленных выше направлениях, а также способствуют более осмысленному выполнению арифметических действий, их обоснованию изученными теоретическими знаниями.
Исследовательские задания на основе старинных задач
В качестве примера приведем одну из старинных задач и покажем возможность организации деятельности детей на каждом этапе исследования.
Задача. Журавли обыкновенно летают так, что образуют правильный треугольник: впереди один журавль (вожак), за ним 2, потом 3 журавля и т.д. Сколько летело в стае журавлей, если в последнем ряду можно было их насчитать 15 штук?
Схематический рисунок ситуации представлен на рис. 1.

На этапе анализа информации после составления интересующей нас суммы 1 + 2 + + 3 + … + 15 можно рассказать ученикам про великого немецкого математика Карла Фридриха Гаусса (1777-1855), которого называли "королем математики". Он нашел способ решения подобных примеров в возрасте девяти лет.
Для того чтобы учащиеся могли догадаться, как это легче сделать, можно сначала взять 10 слагаемых или меньше, например, 8 или 6.
На этапе постановки проблемы обращаем внимание, что складывать все числа подряд долго и неудобно. Надо найти более легкий способ сложения. В ходе его поиска можно использовать меньшее количество слагаемых, изобразив их кругами или квадратами.
На этапе выдвижения гипотезы можно провести дополнительный анализ каждой суммы, используя предметные или графические модели. Предметная модель суммы чисел от 1 до 8 предложена в книге Н.Н. Аменицкого и И.А. Сахарова. Авторы предлагают сначала сделать 8 карточек с кругами от 1 до 8, потом еще 8 карточек с кругами от 8 до 1 и разложить их в 2 ряда (рис. 2).
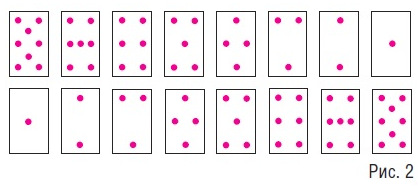
Два ряда состоят из 8 столбиков, в каждом столбике по 9 кругов. Всего 9 - 8 = 72 (круга) или (8 + 1) - 8 = 72 (круга), а в одном ряду содержится половина кругов: 72: 2 = 36.
Можно дать задание: "Рассмотри записи и объясни, как можно рассуждать при вычислении суммы 1 + 2 + 3 +... + 7 + 8".
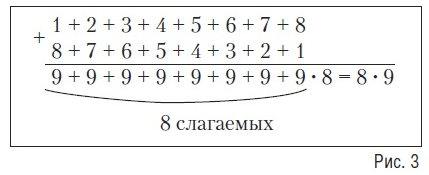
Это удвоенная сумма чисел от 1 до 8, поэтому ее надо разделить на 2. Получилось равенство
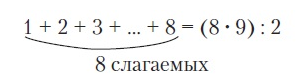
В этом равенстве сумма первых 8 чисел равна половине произведения количества слагаемых (или последнего слагаемого) на следующее число (т.е. на 1 больше последнего слагаемого).
На этапе проверки гипотезы можно изобразить аналогичную сумму
1 + 2 + 3 + 4 + 5 + 6 (с другим количеством слагаемых) в виде числовой лесенки (см. рис. 4, а) и предложить ученикам объяснить, как из двух лесенок (рис. 4, б) получили прямоугольник на рис. 4, в.
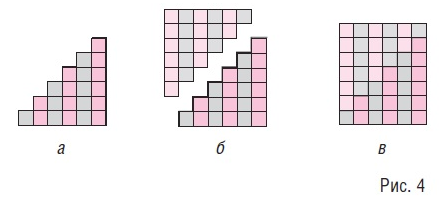
Затем учащиеся находят общее количество клеток в прямоугольнике и в одной лесенке и объясняют по рисункам следующие выражения и равенства:
1 + 2 + 3 + 4 + 5 + 6;
(1 + 2 + 3 + 4 + 5 + 6) - 2;
6 - (6+1);
(1 + 2 + 3 + 4 + 5 + 6) - 2 = 6 - (6 + 1);
1 + 2 + 3 + 4 + 5 + 6 = 6 - (6 + 1): 2.
После этого выполняются вычисления, необходимые для решения исходной задачи: 1 + 2 + 3 +... + 15 = (15 - 16): 2 = 120 (журавлей).
На этапе формулирования выводов можно перенести подмеченную закономерность на любое количество последовательных слагаемых от 1 до п, а потом решить задачу Гаусса.
Найдем сумму чисел от 1 до п: 1 + 2 + 3 +... + п, где п — какое-то натуральное число. Что тогда означает п + 1? Это следующее за п число. Запишем равенство (формулу) для нахождения суммы чисел от 1 до п:
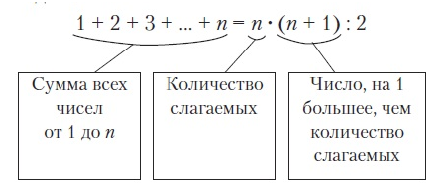
Если использовать эту формулу, то сумма всех чисел от 1 до 100 равна: S=1+2 + 3 + 4 +... + 99 + 100 = 100 - 101: 2 = 5050.
При решении данной задачи использовано графическое моделирование ситуации, что позволяет ученикам наглядно представить ее, лучше понять и решить поставленную перед ними проблему.
На этапе применения выводов можно уточнить реальность ситуации, рассмотренной в старинной задаче. На самом деле журавли летают не треугольником, а клином. На рис. 1, моделирующем ситуацию, надо убрать все серые круги, изображающие птиц внутри клина. Ученики должны догадаться, как надо применить полученные знания для вычисления количества птиц клине:
(1 + 2 +... + 15) – (1 + 2 +... + 13) = 120 – 13 - 14: 2 + 120 – 91 = 29 (птиц).
Большие возможности для развития исследовательских умений младших школьников на уроках математики дают различные интерактивные задания исследовательского характера.
Рассмотрим роль интерактивных заданий для развития одного из исследовательских умений – умения устанавливать влияние изменения условий на изменение свойств объекта. Это умение, в отличие от многих общих исследовательских умений, требующих высокого уровня мыслительной деятельности (и доступных лишь в старших классах), можно начать формировать уже в младших классах.
Математика отличается абстрактностью объектов, а исследовательская деятельность с математическим содержанием носит преимущественно мыслительный характер. С помощью интерактивных заданий можно сделать видимыми, наглядными изучаемые процессы, сложные для понимания. Интерактивные задания, как форма компьютерной поддержки обучения математике, больше всего подходят для развития исследовательского умения устанавливать влияние изменения условий на изменение объекта. Интерактивные задания хороши тем, что позволяют ученику видеть, как вводимые им данные влияют на ситуацию, к каким изменениям они приводят. При этом можно использовать разные модели: материальные, вербальные, символические, графические. Овладение моделированием как математическим методом и общим методом исследования является одной из целей начального математического образования. Главное отличие компьютерных моделей в том, что они могут быть динамическими. Их использование вместе с другими моделями позволяет ученикам наблюдать процесс изменения и по-разному фиксировать его результат.
Интерактивные задания отличаются от обычных (как на бумажных, так и на электронных носителях) еще и тем, что они направлены не столько на применение имеющихся знаний, сколько на открытие новых, на обобщение знаний. Школьник при их выполнении не может остаться пассивным потребителем знаний, применять их по образцу, ученик находится в позиции активного деятеля, открывающего для себя новое.
В виде интерактивных заданий целесообразно проводить исследования, раскрывающие различные связи и зависимости по всем содержательным линиям начального курса математики, например:
- изменения значения числа от приписывания или отбрасывания нулей в его позиционной записи (при умножении и делении на 10, 100, 1000 и т.п.) (линия числа);
- изменение значения выражения с переменной от изменения значения переменной (элементы алгебры);
- изменения результатов арифметических действий от изменения одного из компонентов (линия арифметических действий над числами);
- пропорциональная зависимость величин (цена, количество, стоимость; длины сторон прямоугольника, его площадь и др.) (линии величин и арифметических сюжетных задач).
При рассмотрении зависимости величин и результатов действий можно выделить два шага. Первый – наблюдение за характером изменения, например, чем больше время движения, тем больше пройденный путь (при постоянной скорости) или чем меньше скорость, тем больше время движения (при постоянном пройденном пути). Второй шаг – количественная характеристика изменения, например, а) при постоянной скорости: во сколько раз увеличили время движения, во столько раз увеличился пройденный путь (прямая пропорциональная зависимость); б) при постоянном пройденном пути: во сколько раз увеличили время движения, во столько раз уменьшилась скорость (пропорциональная обратная зависимость).
Работа в данном направлении вносит вклад в функциональную пропедевтику, помогает детям накопить запас доступных функциональных зависимостей. Это создает основу для изучения идеи функции в основной школе и способствует развитию детей.
В качестве примера рассмотрим интерактивное задание (в 3-х частях) из серии заданий "Что от чего зависит?", которое позволяет выявить и обобщить пропорциональную зависимость величин, связанных с движением. Это задание входит в инструментальную компьютерную среду ИКС, разработанную специалистами РГПУ им. А.И. Герцена и фирмы "Кирилл и Мефодий" Ученикам дается текстовая установка "Наблюдай изменение пройденного пути в зависимости от скорости", которая акцентирует внимание ученика именно на зависимости величин.
Часть 1. На экране видны строчка таблицы, рисунок (его схематический вариант приведен на рис. 1), текст задания: "Введи значение скорости (от 40 до 100 см/сек) и наблюдай изменение пройденного пути (при одинаковом времени)"
|
| Скорость (см/с) | Время ( с) | Пройденный путь (см) |
| 1-й раз | ? | 4 | ? |
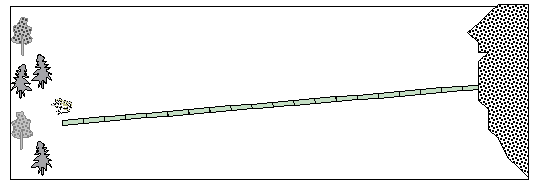
Рис. 1
Ученик вписывает в таблицу значение скорости, лягушка начинает прыгать по дорожке от леса к болоту. На картинке виден процесс движения: за каждую секунду лягушка делает прыжок, длина которого зависит от указанной учеником скорости. После каждого прыжка часть пути меняет цвет. В таблице появляется соответствующее значение пройденного пути. Эта операция повторяется несколько раз. Ученики могут работать самостоятельно, или в парах, обсуждая выбор следующего значения скорости. При этом при введении нового значения скорости можно предложить ученикам, обратить внимание, больше оно или меньше предыдущего, высказывать свои предположения о том, больший или меньший путь (по сравнению с предыдущим) преодолеет лягушка. Динамическое моделирование процесса движения сразу же подтверждает или опровергает высказанное ребенком предположение. После четырех экспериментов на экране появляются итоговый рисунок (его схематический вариант приведен на рис. 2) и итоговая таблица (2), в которой видны вписанные учеником значения скорости и вычисленный компьютером пройденный путь, например:
Таблица 2.
|
| Скорость см/с | Время с | Пройденный путь см |
| (Рис. лягушки в желтом) | 40 | 4 | 160 |
| (Рис. лягушки в красном) | 60 | 4 | 240 |
| (Рис. лягушки в синем) | 70 | 4 | 280 |
| (Рис. лягушки в голубом) | 80 | 4 | 320 |
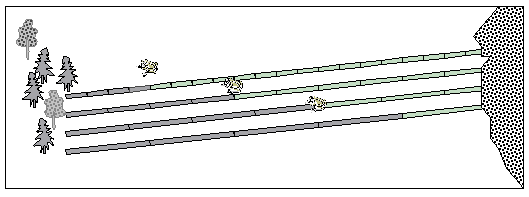
Рис. 2
Дети с учителем анализируют различные модели ситуации (схематический рисунок и заполненную таблицу), выясняют, какая лягушка (в майке какого цвета) проделала больший путь, почему. В таблице можно посмотреть, с какой скоростью она двигалась. Аналогично выясняют, какая лягушка за это же время проделала меньший путь, почему. На этом этапе работы ученики накапливают опыт наблюдений, на основе которого позже ими будет сделан вывод.
Часть 2. Задание ученику: Используя таблицу, выбери в предложении верные слова: "При одинаковом времени движения:
| чем больше скорость, тем | больше | пройденный путь" |
| меньше |
Если слово выбрано верно, оно выделяется красным цветом. (Аналогичная табличка заполняется с ключевым словом "меньше".)
Эта часть работы направлена на то, чтобы ученик подметил направление изменения пути в зависимости от изменения скорости при постоянном времени и сформулировал соответствующий вывод.
Часть 3. Задания ученику:
1) "Для каждой скорости вычисли и запиши значение пройденного пути".
Таблица 3.
|
| Скорость (см/с) | Время (с) | Пройденный путь (см) |
| Рис. лягушки в желтом | 40 | 6 | ? |
| Рис. лягушки в красном | 20 | 6 | ? |
| Рис. лягушки в синем | 10 | 6 | ? |
| Рис. лягушки в голубом | 5 | 6 | ? |
2) "Сравни скорости и пройденные пути при одинаковом времени движения".
Ученикам дается три таблички, в каждой их которых ситуация для сравнения задана рисунком двух лягушек, например:
| (Рис. лягушки в желтом) по сравнению с (рис. лягушки в синем): |
| скорость | больше | в __ раз(а), | пройденный путь | Больше | в __ раз(а), |
| меньше | Меньше |
На основе анализа заполненной таблицы 2 ученики делают вывод о количественной характеристике изменения пройденного пути: во сколько раз больше скорость, во столько же раз больше пройденный путь (при одинаковом времени движения). По таблице 1 такое задание нельзя было дать, т.к. значения скорости, подобранные учеником, могут быть не кратны друг другу.
Если ученик правильно выполнил все задания, то оживает рисунок: по небу плывут облака, на берегу колышется камыш (рогоз) и т.п. Такая реакция компьютера на правильный ответ вызывает у детей эмоциональный отклик.
После выполнения такого задания целесообразно обратить внимание детей, какая величина в данном случае была постоянной, какую величину изменяли сами, а какая изменялась в зависимости от изменений второй. Полезно выяснить, можно ли поменять зависимые величины ролями, какую другую величину сделать постоянной, какую менять по своему желанию, и как будет изменяться третья. Дети могут предложить свои варианты ответов.
Затем полезно провести работу, направленную на еще более широкое обобщение. Для этого можно выяснить с детьми, какие еще величины, известные детям (в том числе по сюжетным арифметическим задачам) связаны такой же зависимостью, как скорость, время, пройденный путь. Спрогнозировать, какую исследовательскую работу с этими величинами можно провести.
Посмотрим на организацию работы детей по выполнению данного интерактивного задания на разных этапах исследовательской деятельности. В данном задании проблема исследования поставлена перед детьми в готовом виде. Однако учитель может так организовать работу на уроке, что, прежде чем обратиться к компьютеру, школьники примут активное участие в анализе исходной информации, в обнаружении, формулировке, осознании проблемы и, может быть, сами выдвинут гипотезу. Обычно выдвижение гипотезы в начальных классах происходит под руководством учителя. Это объясняется тем, что младшие школьники только начинают овладение исследовательской деятельностью. Кларин М.В., Краевский В.В., Лернер И.Я., Фридман Л.М. и др. выделяют три уровня исследовательской деятельности учащихся (1-3) в зависимости от степени их самостоятельности в проведении исследования. Исследовательская деятельность младших школьников находится ниже первого уровня, т.е. на подготовительном уровне. В конкретном классе многое зависит от развития детей, от опыта их исследовательской деятельности, от изобретательности учителя и др. В данном задании выдвижение гипотез может происходить под руководством учителя в процессе подбора скоростей и прикидки того, как это скажется на движении лягушки. Организация эксперимента в случае интерактивного задания продумана без детей, но они целенаправленно наблюдают, как он протекает, убеждаются в его результатах. И здесь учитель может повысить активность детей, организовав предварительное обсуждение того, какой эксперимент можно провести по данной проблеме. Последующие задания (после проведения экспериментальной работы) направляют мысль ученика на анализ данных, полученных в ходе эксперимента, и формулировку выводов. Поскольку работа детей за компьютером имеет строгие ограничения во времени, то задания для применения новых знаний приведены отдельно.
Положительными моментами выполнения исследовательского задания в интерактивном виде являются:
- интерес детей, вызванный формой выполнения задания, способствует лучшему усвоению непростых математических закономерностей, составляющих содержание задания;
- динамическое моделирование процесса, схожесть анимации с реальностью,
- возможность повторения процесса (что не всегда возможно в реальной жизни),
- фиксация экспериментальных результатов для каждого отдельного процесса, что не всегда возможно в реальности и что позволяет выполнить их анализ и обобщение, подвести детей к формулировке выводов;
- использование разных видов моделирования для фиксации результатов (графического, аналитического, вербального), что позволяет детям воспринимать и обрабатывать информацию с помощью различных анализаторов, подключая не только логическое, но и образное мышление.
Главным объективным результатом использования интерактивных исследовательских заданий является развитие самого ученика за счет приобретения опыта исследовательской деятельности, за счет открытия, осмысления, новых знаний, их обобщения, за счет накопления опыта использования компьютерной поддержки в образовательных целях. У школьника эффективнее развиваются исследовательские умения, опыт творческой деятельности, мотивация, самостоятельность, формируется отношение к компьютеру как к средству познания, открытия нового. Задания исследовательского характера обеспечивают понимание школьниками учебного математического материала.
Важна роль таких заданий и в развитии вычислительной культуры школьников: они способствуют развитию мотивации вычислительной деятельности, усвоению различных видов школьного математического языка; воспитывают вдумчивое отношение к числам, раскрывают связи и зависимости между ними; позволяют осознать возможность изменения значения выражения при изменении входящих в него компонентов, способствуют функциональной пропедевтике; формируют опыт осуществления исследовательской деятельности и моделирования.
Исследовательские задачи и формы организации учебной деятельности
В процессе включения школьников в учебно-исследовательскую деятельность перед учителем встает проблема организации решения единых учебно-исследовательских задач при различном уровне развития исследовательского опыта учащихся, это и является основной целью включения школьников в учебно-исследовательскую деятельность. В решении этой проблемы следует исходить из того, что необходимо подбирать такие приемы и формы работы, в которых ученики смогли проявить и обогатить свой индивидуальный исследовательский опыт. Для этого предусмотрена организация учебно-исследовательская деятельность на основе дифференциации и индивидуализации.
Дифференциация деятельности проводится фронтально по отношению ко всему классу и предполагает сочетание как элементов частного и общего («наводящие», дополнительные вопросы и задания), так и элементов репродуктивной и продуктивной деятельности. Такая дифференциация осуществляется преимущественно при коллективном решении проблем. В процессе работы детям оказывается индивидуальная помощь и поддержка. Необходимо активно использовать групповые формы работы. Для этого дети объединяются в группы двумя способами:
способ – в группе объединяются дети с одинаковым уровнем развития исследовательского опыта (по совокупности признаков);
2 способ – в группе работают ученики с различным исследовательским опытом.
Возможны следующие варианты совместной работы:
1. группа выполняет общее задание одновременно на одном и том же «поле труда», но каждый член группы делает свою часть этой общей работы независимо друг от друга;
2. общее задание при тех же условиях выполняется последовательно каждым членом группы;
3. при тех же условиях задача решается при непосредственном одновременном временном взаимодействии каждого члена группы со всеми остальными членами.
Главное, на что стоит ориентироваться при организации групповой работы на уроке – дифференцировать не общие проблемы, а подходы к их решению путем недостающих элементов (подобранных вспомогательных задач). Степень участия каждого школьника в учебно-исследовательской деятельности будет определяться уровнем его активности.
В 5-6 классах уже можно создавать базу исследовательской деятельности:
• методологическую (усвоение структуры исследовательской деятельности и отдельных исследовательских умений и методов, общих и специальных для предмета);
• общую логическую (работа над общими умственными и логическими умениями);
• содержательную (овладение предметными знаниями и умениями);
• субъектную (накопление личностного опыта осуществления исследовательской деятельности). На этой базе легче развивать исследовательскую деятельность учащихся основной школы.
В процессе включения школьников в учебно-исследовательскую деятельность перед учителем встает проблема организации решения единых учебно-исследовательских задач при различном уровне развития исследовательского опыта учащихся, это и является основной целью включения школьников в учебно-исследовательскую деятельность. В решении этой проблемы следует исходить из того, что необходимо подбирать такие приемы и формы работы, в которых ученики смогли проявить и обогатить свой индивидуальный исследовательский опыт. Для этого предусмотрена организация учебно-исследовательская деятельность на основе дифференциации и индивидуализации.
Дифференциация деятельности проводится фронтально по отношению ко всему классу и предполагает сочетание как элементов частного и общего («наводящие», дополнительные вопросы и задания), так и элементов репродуктивной и продуктивной деятельности. Такая дифференциация осуществляется преимущественно при коллективном решении проблем. В процессе работы детям оказывается индивидуальная помощь и поддержка. Необходимо активно использовать групповые формы работы. Для этого дети объединяются в группы двумя способами:
способ – в группе объединяются дети с одинаковым уровнем развития исследовательского опыта (по совокупности признаков);
2 способ – в группе работают ученики с различным исследовательским опытом.
Возможны следующие варианты совместной работы:
1. группа выполняет общее задание одновременно на одном и том же «поле труда», но каждый член группы делает свою часть этой общей работы независимо друг от друга;
2. общее задание при тех же условиях выполняется последовательно каждым членом группы;
3. при тех же условиях задача решается при непосредственном одновременном временном взаимодействии каждого члена группы со всеми остальными членами.
Главное, на что стоит ориентироваться при организации групповой работы на уроке – дифференцировать не общие проблемы, а подходы к их решению путем недостающих элементов (подобранных вспомогательных задач). Степень участия каждого школьника в учебно-исследовательской деятельности будет определяться уровнем его активности.
В 5-6 классах уже можно создавать базу исследовательской деятельности:
• методологическую (усвоение структуры исследовательской деятельности и отдельных исследовательских умений и методов, общих и специальных для предмета);
• общую логическую (работа над общими умственными и логическими умениями);
• содержательную (овладение предметными знаниями и умениями);
• субъектную (накопление личностного опыта осуществления исследовательской деятельности). На этой базе легче развивать исследовательскую деятельность учащихся основной школы.
Деятельность учащихся на уроках математики должна быть организована в соответствии со структурой тематического исследования.
Можно выделить три вида исследовательских заданий по математике, отличающиеся друг от друга присутствием в решении исследовательских компонентов, продолжительностью выполнения и числом учащихся, вовлеченных в решение задания, названные нами условно «урок-исследование», «мини-исследование» и «исследовательский комплекс». Основное назначение этой классификация - выбор оптимального для конкретной ситуации варианта включения исследовательских заданий в процесс обучения, а также демонстрация различных приемов составления исследовательских заданий.
Формирование исследовательских умений, необходимых для успешного выполнения исследовательских заданий происходит по следующему плану:
ознакомление с исследовательским умением посредством решения заданий, содержащих прямое указание на выполнение операций, входящих в состав этого умения;
применение необходимого исследовательского умения при выполнении соответствующего этапа исследования по указанию учителя;
самостоятельный выбор и использование умения, адекватного выполняемому этапу решения исследовательского задания.
В процессе обучения в 5-6 классах происходит постепенная смена способов управления исследовательской деятельностью учащихся (прямые указания — наводящие вопросы — консультирование самостоятельного исследования) и увеличение степени самостоятельности учащихся при проведении исследования: исследование, проводимое совместно с учителем —» исследование по плану с подробными инструкциями —» исследование частных проблем —» исследование по краткому плану —» самостоятельное исследование. Учет интересов учащихся с разными способностями и возможностями обуславливает необходимость разработки исследовательских заданий разного уровня трудности.
Включение исследовательских заданий в процесс обучения математике происходит с учетом стимулов возникновения и развития познавательного интереса к математике. При этом способы организации познавательной деятельности учащихся, играющие основную роль в воспитании познавательного интереса, усиливаются стимулами, связанными с содержанием изучаемого материала и с отношениями между участниками учебного процесса.
Логично считать, что если в учебниках по математике средней школы число задач, формирующих исследовательские умения, будет незначительным, то приобретенные в 5-6 классах элементы таких умений не будут в должной степени развиваться далее, они могут быть утеряны. Тогда в старших классах проблема формирования подобных умений потребует от учителя и ученика гораздо больших усилий. Следовательно, в процессе изучения курса математики в средних классах ученики должны систематически решать задачи, формирующие исследовательские умения, как на уроках, так и во внеурочной деятельности, продолжая работу, начатую в 5-6 классах.
Организация учебно-исследовательской деятельности
Одной из основных тенденций модернизации образования в РК является активизация его развивающей функции. Предполагается, что образовательный процесс в школе должен быть направлен на достижение такого уровня образованности учащихся, который был бы достаточен для самостоятельного творческого решения мировоззренческих проблем теоретического или прикладного характера. Достижение этой цели связывается с организацией учебной деятельности, имеющей исследовательскую направленность.
Особенность профессиональной подготовки учителя к организации учебно-исследовательской деятельности школьников состоит в том, что он не только должен уметь организовывать учебно-исследовательскую деятельность учащихся, но и сам в совершенстве владеть методами научного исследования (уметь формулировать проблему, задачу, вопрос; разработать гипотезу, определить схему эксперимента, найти факторы, пути и средства научного анализа и т.д.).С позиции личностного подхода в качестве ведущего ориентира и главного критерия успешности организации учебно-исследовательской деятельности выступает обогащение исследовательского опыта школьников. Основная задача учителя при этом будет состоять не только в том, чтобы планировать общую, единую и обязательную для всех линию обогащения исследовательского опыта, а в том, чтобы помогать каждому ученику с учетом имеющегося у него опыта совершенствовать свои индивидуальные способности, развиваться как личность.
Задачный подход к организации учебно-исследовательской деятельности означает, что освоение учебного материала происходит посредством решения учебно-исследовательских задач, предполагающих выполнение определенных действий. Основной единицей учебно-исследовательской деятельности является учебно-исследовательская задача, которая формулируется на основе учебного материала, предъявляется школьнику в виде проблемной задачи, а ее решение строится адекватно логике исследования и предполагает определенные действияДля учащихся 5-6 классов основной характеристикой учебно-исследовательской задачи выступает признак проблемности, выполнение же конкретных этапов исследования может протекать с большей или меньшей степенью самостоятельности для ученика. Это связано как с объективной сложностью задачи и задания, так и уровнем подготовленности ученика к выполнению операциональных действий, приемов исследовательской деятельности. Кроме того, в начальных классах подготовка детей к выполнению отдельных исследовательских действий обеспечивается системой исследовательских заданий.
Ситуационный подход к организации деятельности предполагает управление учебно-исследовательской деятельностью как взаимодействие ее субъектов. Его суть состоит в неразрывности прямого и обратного воздействия, органического сочетания изменений воздействующих друг на друга субъектов. Ученическое исследование предполагает не только решение значимых для учащихся проблем, но и овладение способами решения этих проблем. При организации учебно-исследовательской деятельности необходимо создавать учебные ситуации, при разрешении которых учащиеся овладевают знаниями и способами решения проблем в процессе познания в большей или меньшей степени организованного учителем.
Таким образом, организация учебно-исследовательской деятельности на основе единства личностного, ситуационного и задачного подходов предполагает:
• тщательное и систематическое изучение педагогами исследовательского опыта школьников и дифференциацию этого опыта по выраженности различных его составляющих (когнитивного, деятельностного, аксиологического);
• создание учебных ситуаций, при разрешении которых учащиеся овладевают знаниями и способами решения проблем в процессе познания в большей или меньшей степени организованного учителем;
• конструирование системы учебно-исследовательских задач (заданий), сориентированных на поэтапное обогащение исследовательского опыта детей.
Анализ методической литературы показал, что учебно-исследовательская деятельность школьников должна выполнять ряд объективных педагогических требований:
• учитывать возрастные психолого-педагогические особенности мыслительной деятельности;
• основываться на базовом стандарте и служить основой для углубления и получения новых знаний;
• способствовать формированию научного мышления, которое отличается системностью, гибкостью, креативностью;
• содействовать формированию научного мировоззрения;
• стимулировать познавательную активность и развитие творческого потенциала учащихся.
Так как главной целью включения школьников в учебно-исследовательскую деятельность является обогащение исследовательского опыта младших школьников. Этот процесс проходит в несколько этапов:
1. выделение этапов обогащения опыта учащихся 5-6 классов с учетом возрастных особенностей;
2. определение совокупности задач, способов и форм организации учебно-исследовательской деятельности;
3. распределение задач, способов и форм организации учебно-исследовательской деятельности по времени в соответствии с продолжительностью каждого этапа;
4. определение предполагаемых результатов деятельности;
5. отбор содержания и составление учебно-исследовательских задач и заданий.
Из опыта работы по использованию исследовательских заданий
Большим подспорьем в работе учителя по организации творческой учебно-исследовательской деятельности на уроке могут стать нестандартные задания исследования числовых закономерностей. Работая с числовыми закономерностями, ученики открывают для себя немало интересных связей, переживают ситуацию успеха, активно сопереживают одноклассникам в поиске нестандартного решения. Помимо этого у учащихся формируются навыки анализа полученной информации, оппонирования своим товарищам. Заметим, что подобные задания могут быть использованы учителем для развития активного, самостоятельного, творческого мышления школьников на любом этапе урока: при изложении нового материала, закреплении и повторении. Их можно удачно использовать в ходе проведения устного счета, когда каждый школьник должен проявить самостоятельность суждений, смекалку, скорость вычислительных навыков, суметь установить причинно-следственные связи и перенести имеющиеся знания в новую учебную ситуацию. Более того, подобные задания становятся личностно значимыми, стимулируют в каждом ученике стремление дойти до конца, добраться до истины, предложив собственный вариант решения учебной задачи, позволяют каждому школьнику почувствовать себя ученым-первооткрывателем, что, несомненно, способствует эмоциональному подъему на уроке.
Таким образом, учебно-исследовательская деятельность, способствует выработке следующих знаний и умений:
• самостоятельно объяснять и доказывать новые факты, явления закономерности;
• классифицировать, сравнивать, анализировать и обобщать ранее изученные явления, закономерности;
• проводить эксперименты, выдвигать и обосновывать гипотезы;
• устанавливать причинно-следственные связи и отношения;
• рассматривать одни и те же факты, явления, закономерности под новым углом зрения;
• применять научные методы исследования (теоретического анализа и синтеза, экспериментального, моделирования и т.д.);
• находить несколько вариантов решения, выбирать и обосновывать наиболее рациональный;
• рецензировать и оценивать собственную работу исследовательского характера, а также работы товарищей
В приобщении детей к исследовательской деятельности учитель нацелен не на результат, а на процесс. Главное — заинтересовать ребенка, вовлечь в атмосферу деятельности, и тогда результат будет закономерен.
Уровень сформированности исследовательских умений
Один из компонентов учебной исследовательской деятельности – исследовательские умения, которые определяются как система интеллектуальных и практических умений, необходимых для самостоятельного проведения исследования.
Перечислим умения, необходимые при организации учебной исследовательской деятельности:
- умения организовать свою работу (организация рабочего места, планирование работы);
- умения и знания исследовательского характера (выбор темы исследования, умение выстроить структуру исследования, умение определить методы исследования, умение осуществить поиск информации);
- умение работать с информацией (иметь представления о видах информации и источниках информации, умение разделять на смысловые части, умение выделять главное, умение кратко излагать мысли, умение конспектировать и т.д.);
- умение представить результат своей работы (формы представления результатов, формы научных собраний, требования к докладу, речи докладчика);
- оценочные умения (умения, связанные с анализом своей деятельности и с оценочной деятельностью).
Оценить сформированность перечисленных исследовательских умений учащихся начальных классов позволяют следующие критерии:
1. Практическая готовность ученика к осуществлению исследовательской деятельности проявляется в том, что ребенок самостоятельно выбирает значимую для него тему исследования, намечает шаги работы по данной теме, применяет разные методы исследования (работа с литературными источниками, наблюдение и т.д.), оформляет и представляет результат (продукт) своей работы.
2. Мотивированность исследовательской деятельности учащихся рассматривается нами как стремление ребенка узнавать новое, совершать определенные действия для поиска интересующих знаний, участвовать в учебном исследовании. Ученик проявляет познавательную активность в процессе решения учебных проблем, интерес к новым темам и способам работы. Критерий просматривается в динамике у детей мотивов, связанных с ведением исследовательской деятельности: от узких социальных мотивов (добиться похвалы) к широким познавательным (желание найти новое знание, научиться способам нахождения информации).
3. Проявление креативности в учебно-исследовательской деятельности детей учитывалось в подходах к выбору темы, определению задач исследования, в продуктивности при нахождении решений проблем; по оригинальности подходов к выбору путей исследования, созданию нового продукта, оформлению и представлению результатов, умению с разных сторон и позиций видеть исследуемый предмет.
4. Степень проявления самостоятельности. Особенностью младшего школьного возраста является то, что в учебно-познавательной деятельности руководящая роль принадлежит учителю или другим взрослым. Как правило, предмет детского исследования лежит в пределах зоны ближайшего развития ребенка, и ему сложно справиться с исследованием без посторонней помощи. Однако по мере овладения умениями исследовательской деятельности участие взрослых в его работе сокращается, а позиция педагога меняется от руководителя к организатору, помощнику, консультанту.
Оценку каждого из данных критериев можно соотнести с уровнями сформированности умений исследовательской деятельности учащихся младших классов, выявленных и описанных в нашей работе:
1. Исходный уровень мы определяем как уже имеющийся, сформировавшийся на основе спонтанного исследовательского опыта детей и учебных умений, полученных за время обучения в первом классе. Исходному уровню можно дать следующую характеристику: низкий уровень проявления интереса к ведению учебной исследовательской работы, отсутствие знаний об исследовательской деятельности, умений учебно-исследовательской деятельности. Возможна реализация исследовательских действий по аналогии. Ученик редко проявляет инициативу и оригинальный подход в учебном исследовании, не высказывает идей, предложений, предположений по работе.
2. Начальный уровень характеризуется появлением внешних мотивов к ведению исследования, возможностью с помощью учителя находить проблему и предлагать различные варианты её решения. На начальном этапе дети способны выполнять элементарные кратковременные исследования по аналогии с помощью взрослых. Наблюдается владение основами знаний по организации своей исследовательской работы, некоторыми простыми исследовательскими умениями. Проявление креативности можно расценивать как невысокое.
3. Продуктивный уровень обладает следующими характеристиками: устойчивые внутренние и внешние мотивы к ведению исследовательской работы, есть желание вести самостоятельно (индивидуально или с группой) исследование. Учащийся имеет определенные знания об исследовательской деятельности, владеет многими умениями осуществления учебного исследования (может определить тему, цель и задачи исследования с помощью педагога или самостоятельно, работать с источниками информации); демонстрирует возможность оригинального подхода к решению проблемы, представлению результата своей деятельности.
4. Креативный уровень можно определить следующим образом: проявляется постоянный интерес к ведению различного рода исследований, возможность самостоятельно и творчески подходить к выбору темы исследования, умение ставить цель, задачи, продуктивно находить способы решения поставленных задач; высокая доля самостоятельности в реализации работы на всех этапах исследования; умение оригинально представить результат деятельности (Таблица 1).
Таблица 1.
Уровни сформированности исследовательских умений школьников.
| Критерий / Уровни | Практичность в реализации исследования | Мотивированность исследовательской деятельности | Проявление креативности в исследовател. деятельности | Самостоятельность в осуществлении исследовательской деятельности |
| Исходный | Нет знаний и конкретных умений | Низкая | Действия по аналогии | Только под руководством |
| Начальный | Первоначальные знания и элементарные умения | Преобладают внешние процессы | Коллективное творчество | Частичная индивидуальная самостоятельность |
| Продуктивный | Умения, связанные с определением темы, поиском информации в книгах, умения работать с текстом, выделять главное; умения представлять результаты учебного исследования | Внешние и внутренние мотивы к исследованию | Способность выбрать оригинальную тему, интересно представить результаты | Некоторые этапы учебного исследования может осуществлять самостоятельно |
| Креативный | Умения, связанные с определением темы, цели, задач учебного исследования, использованием доступных методов, поиском информации в библиотеке и Интернете, приемами ее фиксации и обработки, составлением графиков, таблиц, схем, рисунков, представлением результата исследования, его анализом и оценкой | Устойчивые внутренние познавательные мотивы | Способность проявлять оригинальность в выборе темы, методов поиска, форм представления результата, высказывать много идей для решения проблем, смотреть на проблему с новой позиции | Практически все этапы учебного исследования может реализовать самостоятельно |
Таким образом, учебно-исследовательская деятельность, способствует выработке следующих знаний и умений:
- самостоятельно объяснять и доказывать новые факты, явления закономерности;
- классифицировать, сравнивать, анализировать и обобщать ранее изученные явления, закономерности;
- проводить эксперименты, выдвигать и обосновывать гипотезы;
- устанавливать причинно-следственные связи и отношения;
- рассматривать одни и те же факты, явления, закономерности под новым углом зрения;
- применять научные методы исследования (теоретического анализа и синтеза, экспериментального, моделирования и т.д.);
- находить несколько вариантов решения, выбирать и обосновывать наиболее рациональный;
- рецензировать и оценивать собственную работу исследовательского характера, а также работы товарищей.
Ранее нами были выделены следующие уровни сформированности исследовательских умений школьников
- исходный уровень (низкий уровень проявления интереса к ведению учебной исследовательской работы; исследовательские умения и навыки проявляются в общей, всем присущей потребности);
- начальный уровень (появления внешних мотивов к ведению исследования; исследовательские навыки и умения появляются в сходных условиях, т.е. по образцу);
- продуктивный уровень (устойчивые внутренние и внешние мотивы к ведению исследовательской работы);
- креативный уровень (творческое проявление исследовательских навыков и умений в новых, неожиданных ситуациях).
Качественный анализ работ показал основные причины затруднения выполнения. Среди них:
а) отсутствие конкретных знаний в решении задач (в 5"А" классе 4 человека – 15%, в 5"Б" классе 3 человека – 12%)
б) недостаточное формирование исследовательских навыков ( в 5 "А" классе 7 человек – 27%, в 5 "Б" классе 8 человек – 31%.)
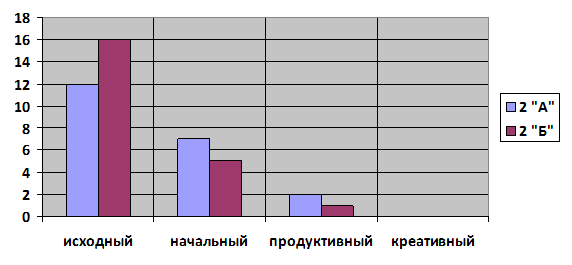
Результаты самостоятельных работ, проведенных в 5 "А" и в 5 "Б" классах представлены на диаграммах 1 и 2.
Диаграмма 1
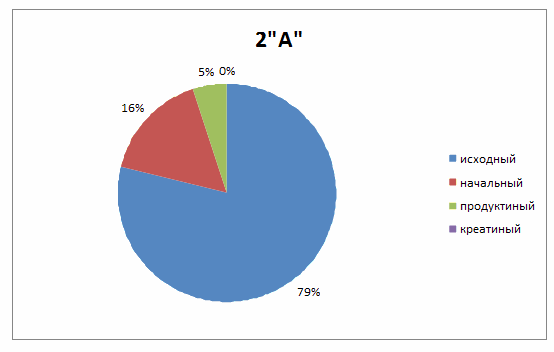
Диаграмма 2
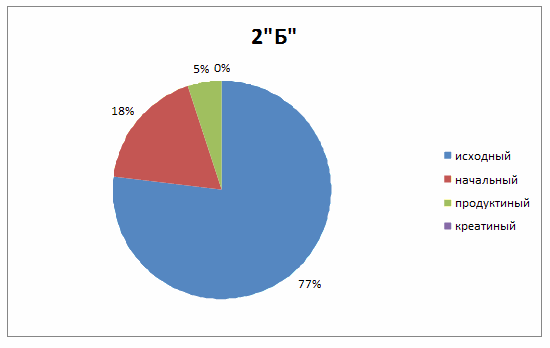
Как видим из диаграмм, средний уровень сформированности исследовательских умений учащихся 5 "А" и 5"Б" классов примерно одинаковый и недостаточно высок в обоих классах.
Гистограмма 1
Уровень сформированности исследовательских умений на первом этапе у 5 "А" и 5 "Б".
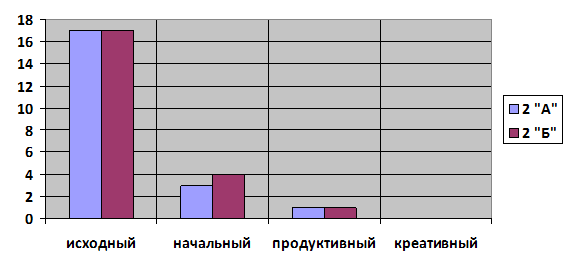
На основании полученных данных были определены экспериментальная и контрольная группы: 5 "А" класс был выбран в качестве экспериментальной группы, а 5 "Б" – в качестве контрольной.
На втором этапе (сентябрь 2014 – октябрь 2014) нами в экспериментальном классе давались различные задания, направленные на повышение уровня исследовательских умений учащихся класса.
.
На третьем этапе (ноябрь 2014) был ещё раз оценен уровень сформированности исследовательских умений учащихся 5 "А" класса (экспериментальная группа) и 5 "Б" класса (контрольная группа). С этой целью учащимся была опять предложена самостоятельная работа
Результаты повторных самостоятельных работ, проведенных в 5 "А" и в 5 "Б" классах предсталены на диаграммах 3 и 4.
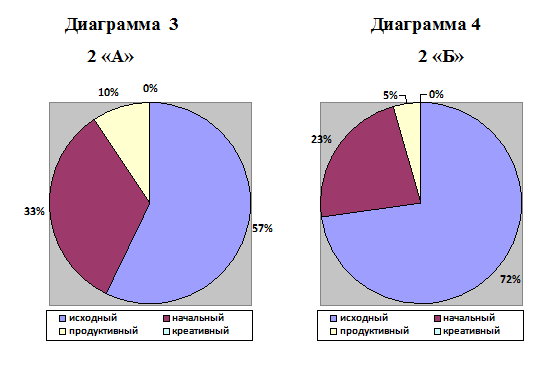
Гистограмма 2 и 3
Уровень сформированности исследовательских умений на первом и третьем этапе у 5 "А" и у 5 "Б".
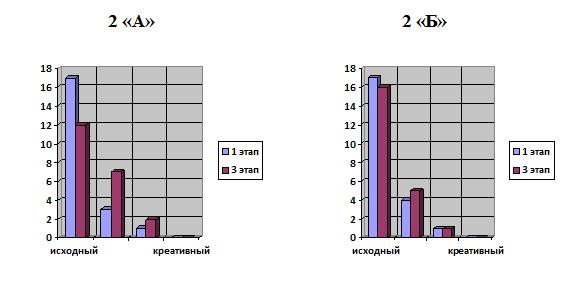
Гистограмма 4
Сравнение уровней сформированности исследовательских умений у 5 "А" и 5 "Б" на 3 этапе.
Анализируя проделанную работу можно сделать ряд выводов:
1. Занятия по развитию исследовательких умений в процессе решения специальных задач на уроках математики в экпериментальном классе были достаточно продуктивны. Нам удалось достичь основной цели данного исследования – на основе теоретического и опытно-экспериментального исследования определить наиболее эффективные формы и методы работы, способствующие развитию исследовательких умений младших школьников при решении задач.
2. Задания исследовательского характера использовались на разных этапах урока. Например, на этапе открытие новых знаний часто создавалась проблемная ситуация, в ходе которой обучающимся предлагалось выполнить задание по новой теме самостоятельно. Учащиеся сами должны осуществить поиск решения задания, а также предложить для поиска решения алгоритмические схемы, блоки и т.п.
На уроках математики некоторым обучающимся предлагается выполнить небольшие индивидуальные исследовательские задания на карточках, поработать над ошибками, которые были допущены при выполнении контрольных, самостоятельных, классных или домашних работах…
Исследовательские задания готовились к уроку заранее, записывались на доске, карточках, схемах. Делились они на два вида:
- обязательные задания - они способствуют умению найти путь выполнения задания, их должно быть огромное количество, они должны быть посильны для каждого ученика.
- дополнительные задания - они рассчитаны на тех учащихся, которые справились с обязательными заданиями и у них есть время для самостоятельной работы. Эти задания повышенной трудности на применение изученного материала, требующие сравнения, исследования, анализа, определенных выводов. Качество и количество упражнений может быть разным, но доступным для усвоения правила на данном этапе урока. В своей практике старалась прививать ученикам интерес к исследованию, тем самым вооружаю их методами научно-исследовательской деятельности. Организовываю работу детей так, чтобы они ненавязчиво усваивали бы процедуру исследования, последовательно проходя все его основные позиции:
- анализ ситуации, принимая во внимание все решения или предположения;
- осознание затруднения и формулировка проблемы, которую надо решить;
- использование предположения как гипотезы, определяющее наблюдения и сбор фактов;
- приведение аргументации и приведение в порядок обнаруженных фактов;
- проведение практической или воображаемой проверки правильности выдвинутых гипотез.
Анализ системы уроков математики выявил следующее. Урок математики, на котором применяются элементы исследования, содержит следующие учебные элементы:
- Ситуация успеха. Ученикам предлагается задачи, которые каждый ученик решает без особых затруднений.
- Ситуация затруднения (ощущения проблемы). Ученикам предлагается задача, похожая на предыдущие, но решить до конца они ее не могут, так как они не имеют еще необходимых знаний.
- Постановка учебной проблемы. Учащиеся, осознав проблему, проговаривают ее, говорят, каких знаний им не хватает, для того чтобы решить задачу, выдвигают гипотезы о возможных путях решения задачи.
- Решение учебной проблемы. Если предложено несколько путей решения проблемы, то возможно деление на группы. Организует деятельность групп лидер, тот ученик, который предложил путь решения незнакомой задачи.
Заключение
Анализ психолого-педагогической и методической литературы, апробирование заданий исследовательского характера в практической деятельности позволяют сделать выводы и обобщения по теме исследования.
Исследовательская деятельность обучающихся играет огромную роль в современных школьных программах. Учебная исследовательская деятельность - это специально организованная, познавательная творческая деятельность обучающихся, по своей структуре соответствующая научной деятельности, характеризующаяся целенаправленностью, активностью, предметностью, мотивированностью и сознательностью, результатом которой является формирование познавательных мотивов, исследовательских умений, новых для учащихся знаний или способов деятельности.
Особенность профессиональной подготовки учителя к организации учебно-исследовательской деятельности школьников состоит в том, что он не только должен уметь организовывать учебно-исследовательскую деятельность учащихся, но и сам в совершенстве владеть методами научного исследования (уметь формулировать проблему, задачу, вопрос; разработать гипотезу, определить схему эксперимента, найти факторы, пути и средства научного анализа и т.д.).
Работа над методическими рекомендациями позволила сделать следующие выводы: одна из главных задач школы и учителя состоит в том, чтобы привить учащимся умения, позволяющие им активно включаться в творческую, исследовательскую деятельность, содействовать формированию и развитию исследовательских навыков и умений у школьников.
В ходе исследования были решены все поставленные задачи и получены следующие основные результаты.
1. На основе анализа различных подходов к выявлению специфики математического мышления и их соотнесения с задачами школьного математического образования конкретизировано содержание проблемы развития математического мышления учащихся. Обоснована взаимосвязь этой проблемы с формированием познавательного интереса школьников к математике.
2. Выявлены психолого-дидактические принципы, лежащие в основе формирования познавательного интереса и развития математического мышления учащихся; ведущими мы считаем принципы деятельности, проблемности и гармонического развития компонентов мышления.
3. Изучена учебная деятельность. моделирующая процесс математического исследования, и в соответствии с ее структурой сформулировано определение исследовательского задания по математике: это учебное задание, выполнение которого предполагает прохождение учеником основных этапов математического исследования (формулировка проблемы, построение математической модели, изучение данных, выдвижение гипотезы, ее доказательство, обобщение и применение результатов), а математическое содержание соответствует курсу 5-6 класса.
4. Проведен анализ особенностей мыслительной деятельности учащихся при решении ими исследовательских заданий. Выявлены качества и компоненты математического мышления, актуализирующиеся на различных этапах учебного исследования, и учебно-исследовательские умения, необходимые для успешного выполнения исследовательских заданий.
5. На основе выделенных в результате теоретического исследования психолого-дидактических принципов развития математического мышления и формирования познавательного интереса учащихся к математике разработана методика включения исследовательских заданий по математике в учебный процесс. Разработаны различные варианты организации учебных исследований на урокахматематики в 5-6 классах и проанализированы возможности и целесообразность их использования на различных этапах обучения.
6. Выделены виды заданий, названные условно «урок-исследование», мини-исследование» и «исследовательский комплекс», отличающиеся уровнем самостоятельности учащихся при их выполнении, присутствием в структуре этих заданий исследовательских компонентов, развивающими функциями и местом в учебном процессе. Предлагаемая методика использования этих заданий на уроках математики и приемы усиления исследовательской нагрузки учебных заданий могут быть применены в практической деятельности учителей общеобразовательных школ, а также могут служить основой для создания методических материалов, реализующих развивающую функцию обучения математике.
7. Экспериментально проверено, что разработанная методика включения исследовательских заданий в процесс обучения математике оказывает эффективное воздействие на развитие математического мышления учащихся и формирование познавательного интереса к математике.
Проведенный педагогический эксперимент показал эффективность разработанной методики реализации системы учебных исследований в процессе обучения учащихся 5-6 классов математике. Таким образом, выдвинутая гипотеза получила подтверждение, и поставленные задачи исследования решены.
Проведенное исследование имеет ряд перспектив, среди которых:
- привлечение компьютерных технологий к проведению учебных исследований;
- определение роли и места метода аналогии в организации учебных исследований;
- разработка методики использования учебных исследований в процессе обучения математике в старших классах, в условиях предпрофильного и профильного обучения
- составление поисково-исследовательских задач межпредметного характера и анализа их влияния на развитие учащихся
Педагогический эксперимент показал, что если в основе решения поисково-исследовательской задачи лежит индуктивный метод, то наиболее приоритетной формой организации обучения является сочетание коллективной и индивидуальной форм учебной работы. Если в основе решения лежит сочетание индуктивного и дедуктивного методов, то наиболее оптимальной формой организации обучения является дифференцированно-групповая форма учебной работы. Дифференцированно-групповую форму учебной работы можно использовать в процессе обучения решению любого класса поисково-исследовательских задач, если использовать уровень «открытости» поисковой задачи.
ПРИЛОЖЕНИЕ 1.
Анкета для учителей математики.
1. Как вы считаете, возможна ли организация исследовательской деятельности обучающихся в 5-6 классах?
2. Какие типы заданий исследовательского характера вы используете на уроках математики (задания на составление задач на основе обобщения, на составление задач обратных данным, с использованием приема аналогии, на исследование свойств объектов, на составление алгоритма решения задач)?
3. Достаточно ли заданий исследовательского характера в учебниках математики 5-6 классов?
4. С какими трудностями сталкиваются обучающиеся при решении задач исследовательского характера?
5. Вызывают ли у школьников интерес задания исследовательского характера?
ПРИЛОЖЕНИЕ 2
Самостоятельная работа № 1
1. Посмотри внимательно на таблицу умножения на 9.
1*9=9
2*9=18
3*9=27
4*9=36
5*9=45
6*9=54
7*9=63
8*9=72
9*9=81
10*9=90
Какие закономерности вы видите?
2. Можно ли множество фигур, изображенных на рисунке, разбить:
а) на две группы – круги и четырехугольники?
3. б) на три группы – четырехугольники, круги и белые фигуры?
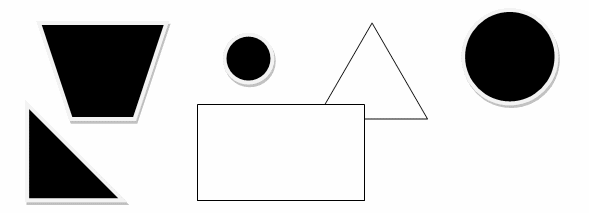
4. Назови группу чисел общим свойством.
2,8,16, 32
2, 4, 5, 7, 9
3, 7, 11, 21
13, 16, 45, 78
345, 666, 793, 900
5. В одном альбоме 48 марок, в другом 37. Поставь вопрос к данному условию. Запиши решение каждой задачи выражением. Вычисли значение всех выражений.
6. На трех этажах гаража стояло 280 автомашин. На втором этаже – 100 автомашин, на третьем – 60. Сколько автомашин стояло на первом этаже? Составь и реши задачу обратную данной.
ПРИЛОЖЕНИЕ 3
Исследование числа
Дано число 546 078.
– Что вы можете рассказать об этом числе? (Оно шестизначное, четное, в его записи использованы цифры 0, 4, 5, 6, 7, 8.) Сколько единиц первого класса, второго класса в этом числе? Найдите сумму цифр в каждом из чисел 546 и 78. (Она одинакова и равна 15.) Выполните действия: 546 + 78,
546 – 78, 546 - 78, 546: 78. (546 + 78 = 624, 546 - 78 = 42588, 546 – 78 = 468, 546: 78 = 7.) Что можно сказать о числах 624 и 468? (В их записи есть одинаковые цифры – 4 и 6.) Из цифр, используемых в записи чисел 468 и 624. оставьте неповторяющиеся цифры 8 и 2. Составьте из них двузначные числа и умножьте их на 7. (28 - 7 = 196, 82 - 7 = 574.) Что интересного вы заметили? (У чисел 196 и 574 одинаковая сумма цифр. Она равна 16.) Найдите значение суммы и разности чисел 574 и 196. (574 + 196 = 770, 574 - 196 = 378.) Определите сумму цифр чисел 770 и 378. (14 и 18.) Разделите числа 770 и 378 на их сумму цифр. (770: 14 = 55, 378: 18 = 21.) Числа 546 и 78 разделите или умножьте на 21. (78 на 21 без остатка не делится. 546 - 21 = 11 466,
78 - 21 = 1 638, 546: 21 = 26.) Что интересного вы заметили? (В записи чисел в равной части равенств есть одинаковая цифра 6.) Выполните деление и умножение с числами 1 638 и 26. (1 638: 26 = 63, 1 638 - 26 = 42 588.) Что интересного вы заметили? (В значении произведения получено число 42 588. Оно также было получено при умножении 546 на 78). Сравните равенства: 546 - 78 = 42 588, 1 638 - 26 = 42 588. (Первый множитель возрастает в 3 раза, а второй – уменьшается в 3 раза, следовательно, значение произведения остается без изменения.)
Исследование ряда чисел
Дан ряд чисел: 13, 17, 21.
– Что можно сказать об этих числах? (Двузначные, нечетные, увеличиваются на 4.) Продолжите ряд влево, уменьшая числа на 4, и вправо, увеличивая числа на 4. (1, 5, 9, 13,17, 21, 25, 29, 33, 37.) Какие числа в получившемся ряду? (Однозначные и двузначные, нечетные.) Разделите их на две равные части посередине и запишите в две строки.
Ученики выполняют запись:
1 5 9 13 17
21 25 29 33 37
– Что интересного вы заметили? (В числах, записанных в каждом столбике, одинаковое количество единиц, а количество десятков в числах второго ряда на 2 больше, чем в числах первого ряда.) Сложите числа каждого столбика (22, 30, 38, 46, 54.) Что можно сказать о них? (Они четные, увеличиваются на 8.) Почему? (Мы дважды увеличили числа на 4.) Используя числа из подчеркнутого ряда, составьте верные равенства.
(17 + 9 – 1 =25, 13 + 17 – 1 = 29, 13 + 25 – 1 = 37, 5 + 9 – 1 = 13,
17 + 5 – 1 =21, 29 + 9 – 1 = 37, 25 – 5 + 1 = 21, 29 – 9 + 1 = 21, 33 – 13 + 1 =21.) Сложите числа из подчеркнутого ряда парами, начиная с самого маленького и самого большого. (1 + 37 = 38. 5 + 33 = 38, 9 + 29 = 38, 13 + 25 = 38,
17 + 21 = 38.) Найдите разность этих чисел. (37 – 1 = 36, 33 – 5 = 28,
29 – 9 = 20, 25 – 13 = 12, 21 – 17 = 4.) Запишите результаты в строчку. (36, 28, 20, 12, 4.) Что можно сказать об этих числах? (Каждое следующее число меньше предыдущего на 8.) Найдите "лишнее" число. Чем оно отличается от других чисел? (4 – однозначное число, остальные числа двузначные.) Разделите каждое число на 4. (36: 4 = 9, 28: 4 = 7, 20: 4 = 5, 12: 4 = 3,
4: 4 = 1.) Что интересного вы заметили? (Значения частных выражены однозначными нечетными числами.)
Исследование суммы
Даны выражения:
42 + 6 35 + 6 27 + 3
46 + 20 36 + 50 23 + 70
– Что можно сказать об этих выражениях? (В выражениях, записанных в верхнем ряду, вторые слагаемые – однозначные числа. Они равны количеству единиц в двузначных числах, являющихся первыми слагаемыми в выражениях нижнего ряда. Цифра, обозначающая количество единиц в первом слагаемом в выражениях верхнего ряда, обозначает и количество десятков второго слагаемого в выражениях нижнего ряда.) Найдите значения сумм данных выражений. (42 + 6 = 48, 46 + 20 = 66, 35 + 6 = 41, 36 + 50 = 86, 27 + 3 = 30, 23 + 70 = 93.) Запишите все двузначные числа из равенств. (42, 48, 46, 20, 35, 41, 36, 50, 27, 23, 70.) На какие группы их можно разделить? (Четные числа: 42, 48, 46, 20, 36, 50, 70; нечетные числа: 35, 41, 27, 23.) Можно ли выделить еще одну группу чисел? (Из четных чисел можно выделить в новую группу числа, обозначающие круглые десятки: 20, 50, 70.) Составьте равенства и неравенства из чисел 20, 50, 70. Расположите четные числа (без круглых десятков) в порядке возрастания и определите закономерность. (36, 42, 46, 48. Числа расположены в порядке возрастания на 6, 4 и 2.) Можно ли продолжить этот числовой ряд по этой закономерности? (Вправо продолжить ряд нельзя, а влево – можно, уменьшая числа на 8, 10, 12 и т.д.) Продолжите. (6, 18, 28, 36, 42, 48.) Что можно сказать об этих числах? (Числовой ряд увеличился на три числа. Число 6, в отличие от всех других чисел, – однозначное.) Найдите пары чисел, при сложении которых не будет перехода через десяток.
Ученики записывают равенства:
36 + 42 = 78 42 + 46 = 88
9 + 6=15 6+10=16
42 + 6 = 48 6 + 6= 12
– Найдите пары чисел, при сложении которых в результате получаются круглые числа. (42 + 18 = 60, 42 + 48 = 90, 44 + 26 = 70.) Найдите пары чисел, при сложении которых необходимо выполнить сложение с переходом через десяток.
Исследование разности.
Даны выражения:
71 – 17 43 – 34 84 – 48
91 – 19 64 – 46
– Что можно сказать об этих выражениях? (В них уменьшаемые и вычитаемые – двузначные числа. Вычитаемые записаны теми же цифрами, что и уменьшаемые, но в обратном порядке). Найдите значения этих выражений. (71 – 17 = 54, 91 – 19 = 72, 43 – 34 = 9, 64 – 46 = 18, 84 – 48 = 36.) Что интересного вы заметили? (Значения разностей 54, 9, 36, 72 и 18 имеют одинаковую сумму цифр – 9. Следовательно, все эти числа делятся на 9.) Расположите значения разностей в порядке возрастания. (9, 18, 36, 54, 72.) Что интересного вы заметили? (Невозможно подобрать двузначные числа, записанные одинаковыми цифрами так, чтобы значение их разности было бы равно 81.) Определите, в каких случаях значение разности чисел, записанных одинаковыми числами, будет наименьшим, т.е. равным 9. (21 – 12, 32 – 23,
43 – 34, 54 – 45, 65 – 56, 76 – 67, 87 – 78, 98 – 89.) Что интересного вы заметили? (Значение разности будет равно 9 в том случае, если уменьшаемое и вычитаемое записаны цифрами, обозначающими числа, которые в числовом ряду расположены рядом и отличаются на одну единицу.) Запишите выражения так, чтобы количество десятков в уменьшаемых было одинаковым, и проверьте свои наблюдения.
Ученики записывают столбики равенств.
91 – 19=72 81 – 18=63
92 – 29=63 82 – 28=54
93 – 39=54 83 – 38=45
94 – 49=45 84 – 48=36
95 – 59=36 85 – 58=27
96 – 69=27 86 – 68=18
97 – 79=18 87 – 78=9
98 – 89=9
71 – 17=54 61 – 16=45
72 – 27=45 62 – 26=36
73 – 37=36 63 – 36=27
74 – 47=27 64 – 46=18
75 – 57=18 65 – 56=9
76 – 67=9
51 – 15=36 41 – 14=27
52 – 25=27 42 – 24=18
53 – 35=18 43 – 34=9
54 – 45=9
32 – 23=9 21 – 12=9
31 – 13=18
После того как будут обобщены результаты действий по всем числам, можно сделать выводы: а) значение разности, равное 9, есть во всех столбиках, равное 72 – в одном случае (91 – 19); б) с уменьшением количества десятков в уменьшаемом уменьшается и количество значений разности.
– Запишите в порядке возрастания числа, которые использовались для обозначения количества десятков и единиц в данном упражнении. (1, 2, 3, 4, 5, 6, 7, 8, 9.) Можно ли, пользуясь отрезком числового ряда, назвать результат вычитания чисел, записанных одинаковыми цифрами, не производя вычислений?
С помощью учителя школьники могут прийти к следующему выводу: "Мы сможем назвать не результат, а подсказку, которая укажет на количество десятков в значении разности. Рассмотрим, например, выражение 81 – 18. Для записи чисел 81 и 18 использованы цифры 8 и 1. Расположим соответствующие им однозначные числа 1 и 8 на числовом ряду и увидим, что между ними располагаются 6 чисел. Именно столько десятков будет в результате вычитания чисел 81 и 18. Проверим: 81 – 18 = 63".
– Проверьте этот, взяв любые пары чисел.
Затем учитель сообщает, что между рядом стоящими в ряду числами
1 и 2, 2 и 3, 3 и 4, 4 и 5, 5 и 6, 6 и 7, 7 и 8, 8 и 9 нет "промежуточного числа", значит, в значении разности чисел, записанных этими цифрами, будут отсутствовать десятки, т.е. ответ будет равен 9, и предлагает ученикам проверить это наблюдение, выполнив вычитание.
Учитель обращает внимание младших школьников на то, что если количество десятков в уменьшаемом равно 9, например, в выражении
91 – 19, то по такому же отрезку числового ряда можно найти указание на количество единиц в значении разности. Запишем отрезок числового ряда от 1 до 9: 1, 2, 3, 4, 5, 6, 7, 8. Закрываем числа 1 и 9. Между ними 7 чисел – это количество десятков в значении разности. Найдем наименьшее число в открытой части ряда. Это число обозначает количество единиц в значении разности. Проверим: 91 – 19 = 72.
Затем учитель предлагает проверить данное наблюдение на других числах.
Исследование произведения
– Найдите значения произведений 13 - 3, 19 - 3, 15 - 3, 12 - 3 и запишите их (39, 57, 45, 36.) Что вы можете сказать об этих числах? (Они двузначные, одно четное, остальные нечетные.) Расположите эти числа в порядке возрастания, определите, есть ли в полученном числовом ряду закономерность. (36, 39, 45, 57. Числа увеличиваются на 3, 6, 12.) Продолжите ряд по заданной закономерности до числа, в записи которого есть одинаковые цифры. (36, 39, 45, 57, 81, 129, 225.) Объедините эти числа в группы. (Двузначные числа: 36, 39, 45, 57, 81; трехзначные числа: 129, 225; нечетные числа: 39, 45, 57, 81, 129, 225; четное число 36.) Определите сумму цифр каждого числа.
Для наглядного выявления закономерности лучше записать это задание в две строки:
| Числа | 36 | 39 | 45 | 57 | 81 | 129 | 225 |
| Сумма цифр | 9 | 12 | 9 | 12 | 9 | 12 | 9 |
– Что интересного вы заметили? (В нижней строке числа 9 и 12 чередуются.) Вычтите все двузначные числа из подчеркнутого ряда из 129. (129 – 36 = 93, 129 – 39 = 90, 129 – 45 = 84, 129 – 57 = 72, 129 – 81 = 48.) Найдите сумму цифр значений разности. (12, 9, 12, 9, 12.) Что интересного вы заметили? (Опять повторяются числа 12 и 9.) Умножьте двузначные числа из подчеркнутого ряда на 6. (36 - 6 = 216, 39 - 6 = 234, 45 - 6 = 270,
57 - 6 = 342, 81 - 6 = 486.) Найдите сумму цифр значений произведений. (Сумма цифр всех чисел, кроме числа 486, равна 9.) Образуйте из цифр, которые использованы для записи числа 486, все возможные трехзначные числа. (486, 468, 648, 684, 846, 864.) Найдите число, в котором наибольшее количество единиц и наименьшее количество десятков. (Это число 648.) Разделите число 648 на однозначные числа. (648: 2 = 324, 648: 3 = 216,
648:4 = 162, 648: 6 = 108, 648: 8 = 81. 648: 9 = 72.) Определите сумму цифр значений частных. (Она равна 9.)
Исследование частного
– Предположите, какие числа (39, 13, 52 и 26) будут значениями частных 871: 67,
1 846: 71, 2 262: 58, 2 392: 46. Проверьте, выполнив деление. (871: 67 = 13, 2 262: 58 = 39, 1 846: 71 = 26, 2 392: 46 = 52.) Расположите значения частных в порядке возрастания. (13, 26, 39, 52) Что интересного вы заметили? (Числовой ряд является закономерностью: каждое следующее число больше предыдущего на 13.) Продолжите ряд на множестве двузначных чисел. (13, 26, 39, 52, 65. 78, 81, 94) Среди цифр, используемых при записи делимых, найдите цифры, которые использованы один раз. (7, 4, 3, 9.) Исключите лишнее число. (Это число 4, оно четное.) Используя цифры 7, 3 и 9, составьте наибольшее и наименьшее числа. (379, 973.) Найдите значение разности этих чисел. (973 – 379 = 594.) Умножьте число 594 на значения частных: 13, 26, 39, 52. (594 - 13 = 7722, 594 - 26 = 5 444, 594 - 39 = 23 166, 594 - 52 = 30 888.) Что интересного вы заметили в числах, обозначающих значения произведении? (Для их записи использованы не менее двух одинаковых цифр.) Разделите число 30 888 на числа из подчеркнутого ряда.
Ученики выполняют вычисления.
30 888:13=2376
30 888:26=1188
30 888:39=792
30 888:52=594
30 888:65=545 (ост.13)
30 888:78=396
30 888:81=381 (ост.27)
30 888:94=328 (ост.56)
– Найдите сумму цифр значений частных в случаях деления без остатка. (Она равна 18.) Разделите 30 888 на 18. (Получится 1 716.) Установите зависимость между числами: 13, 26, 39, 52 и 78.
Учащиеся записывают равенства.
78:13 = 6 52:13 = 4 26: 13 = 2
78: 26 = 3 52: 26 = 2 39: 3 = 3
78: 39 = 2
– На основании выявленной зависимости между числами предположите, какая может быть зависимость между значениями частных при делении 1 716 на 13, 26, 39, 52 и 78. (При одинаковом делимом значения частных уменьшаются во столько раз, во сколько раз увеличиваются делители.)
ПРИЛОЖЕНИЕ 4
Самостоятельная работа № 2
1. Посмотри внимательно на часть таблицы умножения на 8.
1*8=8
2*8=16
3*8=24
4*8=32
5*8=40
Какие закономерности вы видите?
2. Можно ли множество фигур, изображенных на рисунке, разбить:
а) на две группы – круги и четырехугольники?
б) на три группы – четырехугольники, круги и белые фигуры?
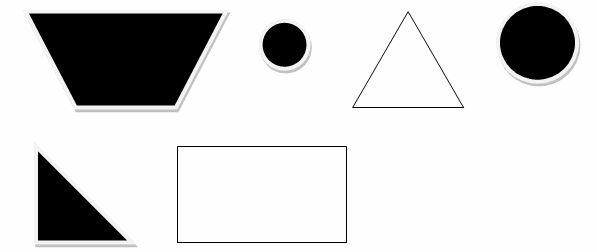
3. Назови группу чисел общим свойством.
5,7, 13, 25 –
15, 18, 47,76 –
347, 686, 893, 900 -
4. В одной корзине 36 грибов, а другой – 24. Поставь вопрос к данному условию. Запиши решение каждой задачи выражением. Вычисли значения этих выражений.
5. На трех книжных полках стояло 170 книг. На второй полке – 60 книг, на третьей – 50. Сколько книг стояло на первой полке? Составь и реши задачу обратную данной.
Приложение 5.
Займемся исследованием чисел
В разделе предлагаем изучить один класс натуральных чисел.
Задание 1. Изучите следующие натуральные числа:
11; 22; 1230, 2301; 4211; 2411; 4112; 101; 1235; 1245; 2255; 1236; 6321; 3216.
Какое из чисел является «лишним»?
Задание 2. Школьник назвал «лишним» числом 1235. Согласны ли Вы с таким решением.
Задание 3. Назовите общее свойство таких чисел:
11; 22; 1230, 2301; 4211; 2411; 4112; 101; 1245; 2255; 1236; 6321; 3216.
Задание 4. Какое из чисел 2349 или 3469 имеет то же свойство, что и числа
11; 22; 1230, 2301; 4211; 2411; 4112; 101; 1245; 2255; 1236; 6321; 3216?
Задание 5. Назовите два общих свойства чисел:
11; 101; 1001; 1100.
Назовите еще два числа, содержащих не более двух цифр, которые обладают этими же двумя общими свойствами.
Имеет ли те же свойства число 10001. Назовите другие числа, которые имеют те же свойства.
Задание 1
Исследуем и применяем последние цифры степеней
| Последняя цифра nk | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| n1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| n2 | 0 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 |
| n3 | 0 | 1 | 8 | 7 | 4 | 5 | 6 | 3 | 2 | 9 |
| n4 | 0 | 1 | 6 | 1 | 6 | 5 | 6 | 1 | 6 | 1 |
| n5 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| n6 | 0 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 |
| n7 | 0 | 1 | 8 | 7 | 4 | 5 | 6 | 3 | 2 | 9 |
Покажем, каким образом можно составить задачи, используя данные этой таблицы.
Шаг 1. С помощью таблицы находим последние цифры новых чисел. В нашем примере последовательно найдены последние цифры чисел 2n2 (Третья строка) и 2n2+n (четвертая строка).
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| n1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| n2 | 0 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 |
| 2n2 | 0 | 2 | 8 | 8 | 2 | 0 | 2 | 8 | 8 | 2 |
| 2n2+n | 0 | 3 | 0 | 1 | 6 | 5 | 8 | 5 | 6 | 1 |
Шаг 2. Выписываем все последние цифры {0; 1; 3; 5; 6; 8}.
Шаг 3. Выбираем число, которого нет в этом списке. К примеру, выбрали число 4.
4. Формулируем задание (приводим разные формулировки):
А) Существуют ли натуральные числа n такие, что 2n2+n=1004?
Б) Доказать, что не существует натуральных n таких, что 2 n2+ n=1004.
В) Сколько существует натуральных n таких, что 2 n2+ n=1004.
Г) Существует ли цифра такая, что натуральное число n оканчивается на эту цифру 2 n2+ n = 105. Сколько таких цифр?
Задание 1. Предложите свои задачи с натуральными числами.


 Получите свидетельство
Получите свидетельство Вход
Вход






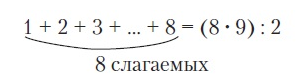




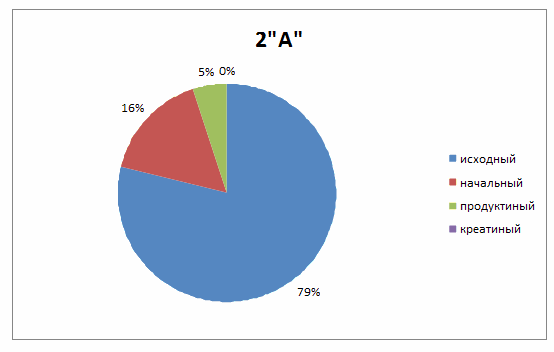
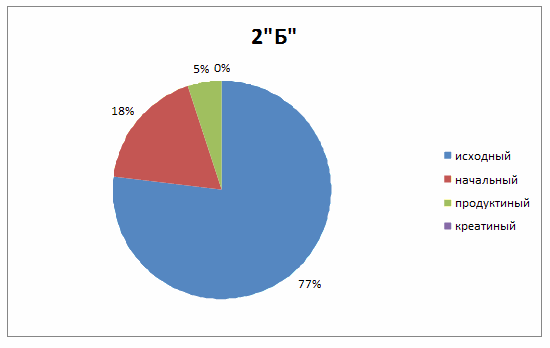















 Проект по математике "Составление исследовательских задач по математике" (0.4 MB)
Проект по математике "Составление исследовательских задач по математике" (0.4 MB)
 0
0 6472
6472 526
526 Нравится
0
Нравится
0


