Муниципальное бюджетное образовательное учреждение
«Средняя общеобразовательная школа № 68»
«Функции вокруг нас.
Необычное в привычном»
Секция: «Созидательная сила великих открытый в математике»
Автор: Синенкова
Александра Дмитриевна,
ученица 9 класса «А»
МБОУ СОШ № 68
Руководитель: Моренкова
Наталья Юрьевна,
учитель математики
I квалификационной категории
МБОУ СОШ №68
г. Дзержинск
2014 год
Оглавление
Введение …………………………………………………………………3
I. Функции в математике.
1. Из истории возникновения функции. Определения функции..4
2. Способы задания функции, особенности. График функции….5
3. Виды функций, типы функций, некоторые характеристики….6
II. Функции вокруг нас
1. Многообразие значений слова «функция»……………………..9
2. Мой первый в жизни график…………………………………….9
3. Кардиограмма – график работы сердца……………………….10
4. Мороженое и кусочно-линейная функция……………………..11
5. «Великий и могучий русский язык…»…………………………13
6. Функции и юмор
6.1. Закон Подлости……………………………………………16
6.2. Законы Мерфи……………………………………………..17
III. Заключение…………………………………………………………..21
IV. Список использованных источников и литературы………….22
Введение
«Когда математика стала изучать
переменные величины и функции,
как только она научилась
описывать процессы, движение,
так она стала необходима всем».
Ф.Энгельс
Наука неисчерпаема, но этим она и интересна. Познание ее приносит человеку настоящую радость. Каждая область знаний: физика, химия, биология, социология, лингвистика и т. д. имеет свои объекты изучения, устанавливает свойства и, что особенно важно, взаимосвязи этих объектов.
Функции – математические портреты устойчивых закономерностей природы. Функции позволяют воспринимать зависимость различных величин как живой, изменяющийся процесс. Человек, владеющий ими, способен видеть процесс взаимосвязи явлений окружающего мира в динамике. Это помогает проникать в саму суть физических явлений, заданных аналитически, позволяет решать сложные задачи графически, осуществлять переход от формулы к функциональной зависимости.
В различных науках и областях человеческой деятельности возникают количественные соотношения, и математика изучает их в виде свойств чисел. Математика рассматривает абстрактные переменные величины и в отвлеченном виде, изучает различные законы их взаимосвязи, которые на математическом языке называются функциональными зависимостями, или функциями. И где бы конкретно ни появилась эта зависимость, сделанное абстрактное математическое заключение можно применять в конкретной ситуации к любым конкретным объектам.
Наблюдая различные процессы и явления, мы стараемся разглядеть самые существенные их черты, самые глубокие закономерности. Часто они оказываются общими для широчайшего круга наблюдаемых событий. Общей оказывается и математическая модель, построенная на основе этих закономерностей.
Функция – это одно из основных общенаучных и математических понятий, выражающее зависимость между переменными величинами.
Математические формулы – лишь удобный язык для изложения идей и методов математики. Сами же эти идеи можно описать используя привычные и наглядные образы из окружающей жизни.
Систематизируя наиболее устойчивые и поддающиеся осмыслению взаимозависимости, человек научился рассматривать их, как частный случай сравнительно немногих общих соотношений. Человек назвал их законами природы. Знание законов природы дало человеку возможность объяснить и предсказывать её разнообразнейшие явления.
Всем известно, что без математики не существует ни одна наука. Как сказал К.Ф. Гаусс: «Математика – царица наук». Бесспорно, ее значение и применение в физике, химии, биологии, экономике, географии, информатике, логистике и других науках трудно переоценить. В них она нужна как строгий, необходимый инструмент, без которого существование этих наук было бы невозможно. Метапредметные и межпредметные связи между этими науками изучаются в школьном курсе. Я считаю, что в изучении любого предмета должна быть связь с реальной жизнью.
В рамках одной работы невозможно полностью показать все многообразие применений функций и их исследований, поэтому
целью моей работы является показать некоторые примеры нестандартного взгляда на применение математических понятий и функций в окружающей нас жизни.
То, что на первый взгляд ускользает из поля зрения, и на что не всегда можно обратить внимание.
Тем не менее, это очень интересно и познавательно - видеть знакомое в незнакомом!
I. Функции в математике
1. Из истории возникновения функции. Определения функции.
Люди впервые поняли, что окружающие их явления взаимосвязаны, достаточно давно. Они ещё не умели считать, писать, но уже интуитивно чувствовали, и на практике проверяли некоторые закономерности и делали выводы. С развитием скотоводства и земледелия, ремесла и обмена увеличилось количество известных людям зависимостей между величинами.
Идея функциональной зависимости восходит к древности, она содержится уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами, в первых формулах для нахождения площади и объема тех или иных фигур.
Однако явное и вполне сознательное применение понятия функции и систематическое изучение функциональной зависимости берут своё начало в XVII в. в связи с проникновением в математику идеи переменных. Оно сыграло и поныне большую роль в познании реального мира.
Чёткого представления понятия функции в XVII в. ещё не было, однако путь к первому такому определению проложил Декарт, который систематически рассматривал в своей «Геометрии» лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться таким образом с понятием аналитического выражения – формулы.
Термин «функция» (в некотором более узком смысле) был впервые использован Лейбницем (1692 год).
Первоначально понятие функции было неотличимо от понятия аналитического представления. Впоследствии появилось определение функции, данное Эйлером (1751 год), затем — у Лакруа (1806 год) — уже практически в современном виде. Наконец, общее определение функции (в современной форме, но для числовых функций) было дано Лобачевским (1834 год) и Дирихле (1837 год).
К концу XIX века понятие функции переросло рамки числовых систем. Первыми это сделали векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.
Слово «функция» (от латинского functio – совершение, выполнение) Лейбниц употреблял с 1673 г. в смысле роли (величина, выполняющая ту или иную функцию). Как термин в нашем смысле выражение «функция от x» стало употребляться впервые в 1718 г. одним из учеников и сотрудников Лейбница, выдающимся швейцарским математиком Бернулли: «Функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных». Оно привело в восхищение престарелого Лейбница, увидевшего, что отход от геометрических образов знаменует новую эпоху в изучении функций.
Многие из этих функций нельзя было явно выразить с помощью ранее известных операций. Поэтому один из самых замечательных математиков XVII в. Леонард Эйлер (1707 – 1783), вводя в своём учебнике понятие функции, говорит лишь, что «когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых».
Леонард Эйлер во «Введении в анализ бесконечных» (1748) примыкает к определению своего учителя И. Бернулли, несколько уточняя его. Определение Л. Эйлера гласит: «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего XVII в. Даламбер, Лагранж и другие видные математики.
В формировании современного понимания функциональной зависимости приняли участие многие крупные математики. Описание функции, почти совпадающее с современным, встречается уже в учебниках математики начала XIX в. Активным сторонником такого понимания функции был Н.И. Лобачевский.
Почему мы обозначаем функцию символом f, и когда он появился? Этот символ изобрел в 1733 г. французский математик Клеро. А появился этот символ, когда формировался общий подход к понятию функции, когда потребовалось обозначение «функции вообще».
Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между какими-либо значениями. Можно сказать, что функция — это «закон», по которому одна величина зависит от другой величины.
Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины.
Часто под термином «функция» понимается числовая функция; то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.
Понятие функции можно считать стержнем, вокруг которого группируется преподавание математики. Никакое другое понятие не отражает явлений реальной действительности с такой конкретностью, как понятие функциональной зависимости.
Облик каждой функции можно представить сложенным из набора характерных деталей. В них проявляются основные свойства функций. Наблюдая различные процессы и явления, мы стараемся разглядеть самые существенные их черты, самые глубокие закономерности. Часто они оказываются общими для широчайшего круга наблюдаемых событий.
Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.
1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами. Любой физический закон, любая формула отражает такую взаимосвязь величин.
Знакомое обозначение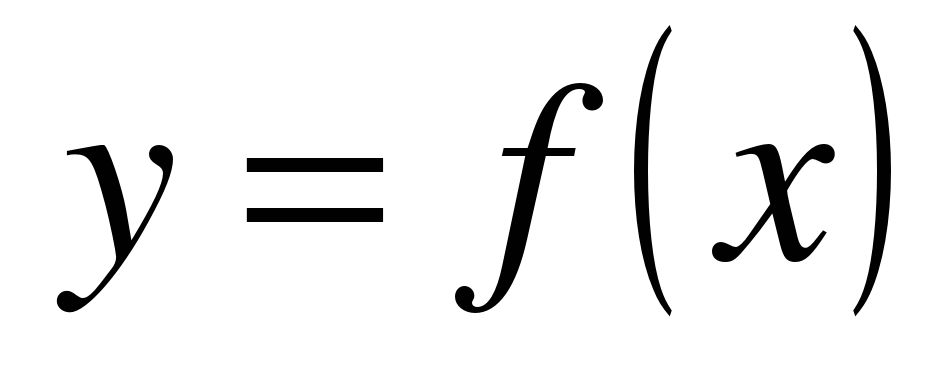 
как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины x по определенному закону, или правилу, обозначаемому f.
2. Функция – это определенное действие над переменной.
Это означает, что мы берем величину x, делаем с ней определенное действие (например, возводим в квадрат) – и получаем величину y.
3. В технической литературе встречается определение функции как устройства, на вход которого подается x, а на выходе получается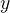 
.
Итак, в данном случае, функция – это действие над переменной.
4. Определение функции, чаще всего встречающееся в учебниках.
Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.
2. Способы задания функции. Особенности. График функции.
Задать функцию – это значит указать ее область определения и правило, при помощи которого по данному значению независимой переменной находятся соответствующие ему значения функции.
1. Табличный способ.
При табличном задании просто выписывается ряд значений независимой переменной и соответствующих им значений функции. Табличный способ особенно распространен в технике, естествознании. Числовые результаты последовательных наблюдений какого-нибудь процесса обычно группируются в виде таблицы. Можно изобразить эту функцию на плоскости, она будет дискретной.
Преимущества: для каждого значения независимой переменной, помещенного в таблице, можно сразу без всяких вычислений найти соответствующее значение функции.
Недостатки: 1. Обычно невозможно задать функцию полностью, найдутся такие значения независимой переменной, которые не помещены в таблице.
2. Отсутствие наглядности при большом объеме таблицы, трудно выявить характер изменения функции.
Пример:
| Х | -1 | 3 | 5 | 7 | 9 | 12 | 15 | 28 |
| Y | 100 | 65 | 23 | 25 | -5 | 43 | 56,9 | 1 |
2. Аналитическое задание (задание формулой).
Аналитическое задание функции состоит в том, что дается формула, с помощью которой по заданным значениям независимой переменной можно получить соотвтетстующие им значения функции. При аналитическом задании функции под областью определения понимают множество значений х, при которых формула, определяющая функцию, имеет смысл.
Аналитическое задание функции – основной способ задания в математическом анализе. Можно построить график функции, она будет не дискретной.
Пример: у = 3х2 – 2х + 5х
Преимущества: 1. Сжатость, компактность задания.
2. Возможность вычислить занчение функции для любого значения независимой переменной из области определения.
3. Возможность применить к данной функции аппарат математического анализа, так как он наилучшим способом приспособлен как раз к аналитической форме задания функций.
Неудобства: 1. Недостаточная наглядность.
2. Необходимость вычислений, нередко очень громоздких.
3. Графическое задание.
Графиком функции (в системе декартовых прямоугольных координат) называется множество всех точек, абсциссы которых являются значениями независимой переменной, а ординаты – соответствующими значениями функции. Масштабы на обеих осях координат могут быть как одинаковыми, так и различными. Графиком функции служит некоторая кривая линия. Понятия линии и функции тесно связаны. Заданием функции порождается линия – ее график; заданием линии порождается функция – та, для которой эта линия служит гарфиком.
Г
рафическое задание функции состоит в задании графика этой функции. В физике и технике функции нередко задаются графически, причем иногда гарфик является единственным доступным средством задания функции. Чаще всего это бывает при употреблении самопишущих приборов, автоматически записывающих изменение одной величины в зависимости от изменения другой. В результате на ленте прибора получается линия, графически задающая регистрируемую прибором функцию.
Преимущества: 1. Наглядность.
2. Единственный способ задания для некоторых функций.
Недостаток: не может быть непосредственно применен аппарат математического анализа.
3. Виды функций. Типы функций. Некоторые характеристики.
1. Основные элементарные функции (степенная, показательная, логарифмическая, тригонометрические, обратные тригонометрические)
2. Элементарные функции. Из основным элементраных функций можно строить другие функции при помощи арифметических действий и операции взятия функции от функции (суперпозиция).
3.Алгебраические и трансцендентные функции.
Виды функций:
1. По способу задания:
- явно заданные (когда в левой части равенства, определяющего функцию, стоит только у, а в правой –выражение, зависящее от х)
- неявно заданные (когда значения функции находятся из уравенния, связывающего и у, и х, но не разрешенного относительно у)
2. По количеству значений
- однозначные (когда каждому х ставится в соответствие только одно значение у)
- многозначные (когда значений у может быть несколько)
Основные характеристики функций.
Изучить заданную функцию –это значит охарактеризовать ход ее изменения (ее поведение) при изменении независимой переменной.
Я рассмотрю не все характеристики функции, а только те, которые мне понадобятся в моем практическом иссследовании.
1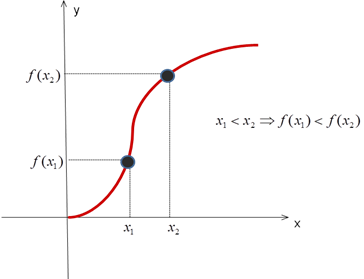
. Возрастание функции
Функция у = f(x) называется возрастающей на множестве , если для любых х1 и х2 множества Х, таких, что х1 х2 выполняется неравенство f(x1) f(x2)
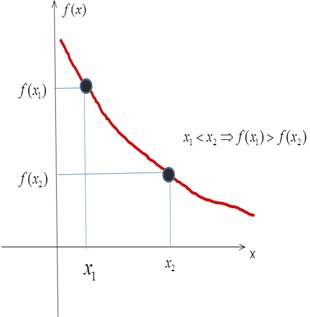
2.Убывание функции
Функция у = f(x) называется убывающей на множестве , если для любых х1 и х2 множества Х, таких, что х1 х2 выполняется неравенство f(x1) f(x2)
3. Ограниченность функции
Н
3
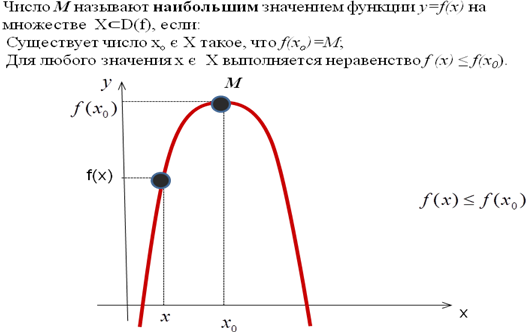
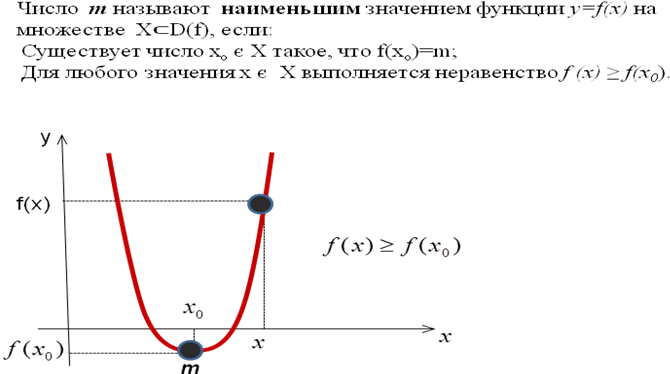
4. Наибольшее и наименьшее значения функции
II Функции вокруг нас
1. Многообразие значений слова «функция»
Значение слова «функция» разнообразно. В толковом словаре Ожегова можно прочитать следующие определения.
Функция, ж. (латин. functio - выполнение работы).
1. Явление, зависящее от другого и изменяющееся по мере изменения этого другого явления (книжн.)
2. Переменная величина, меняющаяся в зависимости от изменения другой величины (мат.).
3. Работа, производимая органом, организмом (биол., физиол.).
4. Обязанность, круг деятельности чего-нибудь, подлежащая исполнению работа (перен.)
5. Значение, назначение, роль (книжн.).
То есть функция затрагивает все сферы нашей жизни, в зависимости от толкования слова. И все эти функции находятся вокруг нас! И представляют широкое поле деятельности для исследования в различных областях, в зависимости от определения слова.
В современный динамично развивающийся мир прочно вошли в обиход различные гаджеты. Мы пользуемся сотовыми телефонами, смартфонами, планшетниками и т.д. Ни одна современная хозяйка не обходится без множества бытовых приборов и разнообразных «помощников». Как мы сравниваем их: что лучше, что удобнее? Какой вопрос мы задаем продавцу, когда хотим приобрести новый товар? Мы всегда спрашиваем о его функциях! Что мы имеем в виду? Нам хочется узнать, какие именно действия может совершать тот или иной агрегат. И слово «функция» приобретает в этом случае еще один смысл: «возможности» прибора. А с этими возможностями напрямую связана и цена, и полезность… А здесь уже можно проследить классическое математическое определение функции - зависимость. Если аппарат обладает множеством функций, значит он более функциональный, то есть удобный. (Зависимость: количество возможностей – удобство, количество возможностей – цена).
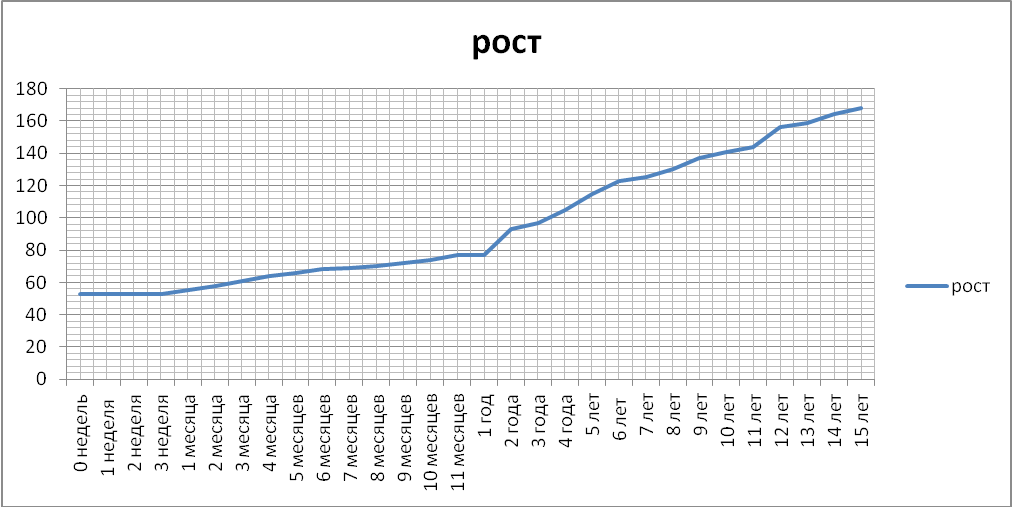
2. Мой первый в жизни график.
Мама сохранила в альбоме данные моего роста с рождения по данный момент времени. Это яркий пример табличного задания функции.
График должен быть дискретным, то есть изображаться на точками на плоскости, так как функция задана только в определенных точках. Но поскольку по физическому смыслу понятно, что при увеличении возраста рост не может уменьшаться, то, не искажая сути, можно считать, что соединение точек прямыми линиями не изменит сущности функции. Для наглядности я эти точки соединила. Получился график моего роста.
| Возраст | 0 недель | 1 н. | 2 н. | 3 н. | 1 мес. | 2 мес. | 3 мес. | 4 мес. | 5 мес. |
| Рост, см | 53 | 53 | 53 | 53 | 55 | 58 | 61 | 64 | 66 |
| Возраст | 6 мес. | 7 мес. | 8 мес. | 9 мес. | 10 мес. | 11 мес | 1 год | 2 года | 3 года |
| Рост, см | 68 | 69 | 70 | 72 | 74 | 77 | 77 | 93 | 97 |
| Возраст | 4 года | 5 лет | 6 лет | 7 лет | 8 лет | 9 лет | 10 лет | 11 лет | 12 лет |
| Рост, см | 105 | 115 | 123 | 125 | 130 | 137 | 141 | 144 | 156 |
| Возраст | 13 лет | 14 лет | 15 лет |
| Рост, см | 159 | 164 | 168 |
3. Кардиограмма – график работы сердца
К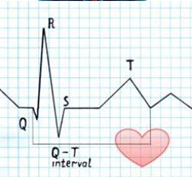
ардиограмма – график работы сердца. Это яркий пример функции, заданной графически. На графике можно увидеть максимум и минимум, фрагменты линейной функции, сглаживание линий и т.д.
Кардиограмма – это запись сокращений сердца человека, которая осуществляется при помощи какого-либо инструментального способа. Во время сокращения сердце передвигается в пределах грудной клетки, оно вращается вокруг своей оси слева направо.
Суть электрографии заключается в том, чтобы зарегистрировать разности потенциала во времени. Кривая, которая показывает нам эти изменения и есть кардиограмма. Прибор, который записывает эту кривую, именуется электрокардиографом. Кардиограмма сердца показывает возбуждение сердца и его сокращение. Во время снятия кардиограммы к телу человека прикрепляются специальные электроды, благодаря которым аппарат и получает необходимые данные.
Суть обработки сигналов данного исследования заключается в том, чтобы диагностировать имеющиеся проблемы в работе сердечных мышц, используя при этом различные аналитические методы. Чтобы диагноз был правильным, прежде всего, необходимо точно установить все особые участки электрокардиограммы в лице зубцов. Здесь в первую очередь важны точная точка их начала и конца. Благодаря этим данным можно вычислить точную ширину, а также амплитуду этих самых зубцов. Именно эти данные чрезвычайно важны для функционального анализа данного исследования. Самой главной проблемой в анализе кардиограммы является то, что все зубцы на ней имеют разную форму, ширину и амплитуду. Довольно часто на некоторых участках кардиограммы зубцов вообще нет.
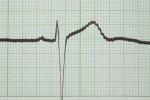
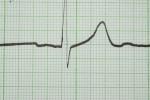
С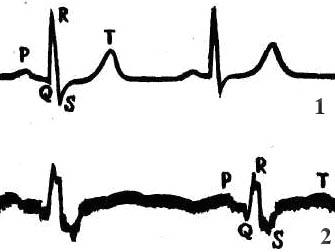
равнивая электрокардиограммы здорового (1) и больного (2) сердца, можно увидеть четкое различие между ними и судить о характере поражения сердечной мышцы. Форма и вид зубцов, длительность и вид промежутков кардиограммы напрямую связаны с фазами возбуждения и расслабления мышц сердца. Работу предсердий характеризует зубец Р (восходящий участок – возбуждение правого, нисходящий – левого предсердий), а промежуток времени, когда действуют оба предсердия, называется PQ. Зубцы Q и R показывают активность нижней и верхней частей сердца. В этот же промежуток времени активны желудочки (их наружные части). Сегмент ST – это активность обеих желудочков, а зубец Т означает переход мышц сердца в нормальное состояние….
И вот так, анализируя каждый участок кардиограммы, врач-кардиолог делает выводы и ставит диагноз. Ему приходится исследовать функцию кардиограммы по разным параметрам. Сравнивать с эталоном по всем критериям, проводить расчеты, сопоставлять цифры.
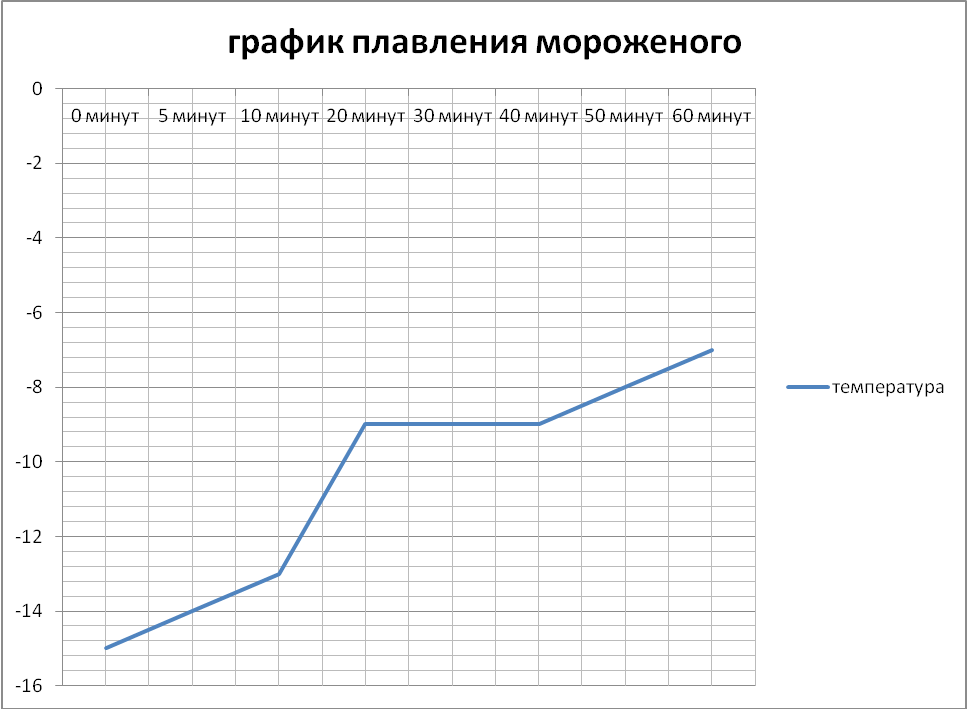
4. Мороженое и кусочно-линейная функция
Переход вещества из твердого состояние в жидкое называется плавлением. Для того чтобы тело начало плавиться, его необходимо нагреть до определенной температуры. Температура, при которой вещество плавится, называют температурой плавления вещества.
Каждое вещество имеет свою температуру плавления. У каких-то тел она очень низкая, например, у льда. А у каких-то тел температура плавления очень высокая, например, железо. Плавление кристаллического тела это сложный процесс.
Н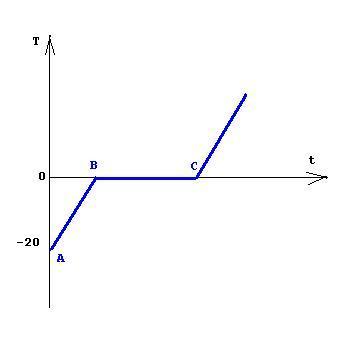
а рисунке представлен известный из курса физики график плавления льда.
График показывает зависимость температуры льда от времени, которое его нагревают. На вертикальной оси отложена температура, по горизонтальной - время.
Из графика видно, что изначально температура льда была -20 градусов. Потом его начали нагревать. Температура начала расти.
Участок АВ это участок нагревания льда. С течением времени, температура увеличилась до 0 градусов. Эта температура считается температурой плавления льда. При этой температуре лед начал плавиться, но при этом перестала возрастать его температура, хотя при этом лед также продолжали нагревать. Участку плавления соответствует участок ВС на графике.
Затем, когда весь лед расплавился и превратился в жидкость, температура воды снова стала увеличиваться. Это показано на графике лучом C. Во время плавления температура тела не изменяется, так как вся поступающая энергия идет на плавление.
Я очень люблю мороженое. Однажды после урока физики, где выполняли практическую работу по наблюдению за плавлением льда, мне захотелось проверить, а будет ли соблюдаться это же правило для мороженого… Именно лед ведь на практике не применяется, и график выглядит уж слишком идеально. Оказалось, что из-за того, что мороженое – это составной продукт, с удельной теплоемкостью, отличающейся от теплоемкости льда, и с другой температурой плавления, график несколько сгладился, но его вид и сущность оказались такими же!
5. «Великий и могучий русский язык…»
Давно замечено, что мудрость и дух народа проявляются в его пословицах и поговорках, а знание пословиц и поговорок того или иного народа способствует не только лучшему знанию языка, но и лучшему пониманию образа мыслей и характера народа.
У русского народа, как у любого другого, существует бесчисленное множество пословиц, поговорок, загадок. Они создавались и накапливались народом в течении многовековой его истории, они отражают его жизнь, условия труда, культуру и т.д. Также они отражают взаимосвязи, существующие между различными жизненными объектами, то есть являются отражениями функциональных зависимостей и доказывают, что функция - это сама жизнь!
Сравнение пословиц и поговорок разных народов показывает, как много общего имеют эти народы, что, в свою очередь, способствует их лучшему взаимопониманию и сближению. В пословицах и поговорках отражен богатый исторический опыт народа, представления, связанные с трудовой деятельностью, бытом и культурой людей.
Необходимо отметить, что многие русские пословицы и поговорки многозначны, что делает их трудными для толкования и сравнения. Тем не менее, важно помнить, что они складывались в различных исторических условиях. И не все пословицы могут быть просто изображены графически.
Главной особенностью пословицы является ее законченность и содержание. Основой пословицы или поговорки является пример жизненной ситуации и иногда подсказка, иногда прямое указание на правильное решение. Пословицы и поговорки составлялись многие столетия и воплощают в себе всю историю развития народа. Пословица всегда поучительна. В ней всегда есть вывод, который полезно помнить каждому.
Я рассмотрела некоторые пословицы и поговорки с точки зрения функциональной зависимости.
Прямая зависимость
Кто много знает, с того много и спрашивается
Еще примеры:
Каков строитель, такова и обитель
Кто много знает, с того много и спрашивается
К чему ребенка приучишь, то от него и получишь
Кто много читает, тот много знает
Как аукнется, так и откликнется
Аппетит приходит во время еды
С плохими косцами плох и укос
Разная скорость роста функции
Без детей горе, а с детьми - вдвое
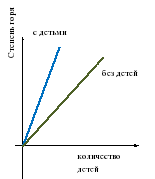
Еще примеры:
Лень, как ржавчина, разъедает быстрее, чем труд изнашивает. (Ф.Рузвельт, 32-й президент США)
О
Меньше говори, больше делай
братная зависимость
Еще примеры:
Работает – как ребенок, а ест – как детина
В умной беседе ума набраться, а в глупой свой растерять
Криво дерево, да яблоки сладки
Худой мир лучше доброй войны
Тише едешь – дальше будешь
На словах густо, а в голове пусто
Не все то золото, что блестит
О
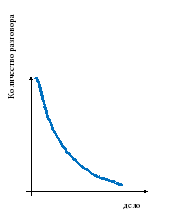
И сокол выше солнца не летает
граниченность/недостижимость
Е
ще примеры:
Бездонную бочку водой не наполнишь
Близок локоть, да не укусишь
Куда Макар телят не гонял
В поле ветра не поймаешь
Поперек себя не перепрыгнешь
Поперек батьки в пекло не суйся
На два, ни полтора
Н
И хорошее кушанье приедается
аибольшее значение функции
Еще примеры:
Крепкую дружбу и топором не разрубишь
Н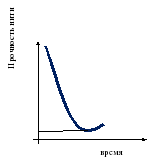
аименьшее значение функции
Где тонко, там и рвется
М
одуль
Что в лоб, что по лбу
П
Дружба дружбой, а служба - службой
араллельные прямые
Еще примеры:
Беда бедой, а еда – едой
Прямая
Для матери ребенок – до ста лет детенок
6. Функции и юмор
6.1. Закон Подлости
Мы часто произносим фразу "как по закону подлости", когда у нас что-то не получается.
Закон Подлости - один из самых древних законов, который был открыт ещё несколько тысячелетий назад. Точная дата открытия, впрочем, как и имя открывшего закон учёного, не дошла до наших дней.
Существует несколько версий относительно того, когда это произошло. Но большинство исследователей придерживаются мнения, что закон был открыт во времена Ахиллеса. Нетрудно догадаться, что привело учёных к этому выводу. Все прекрасно помнят историю непобедимого юноши, слабой стороной которого была пятка. Именно по закону Подлости стрела во время битвы пронзила её Ахиллесу.
Именно это трагическое событие многие и стали считать временем открытия закона. Учёным удалось найти несколько обрывков свитка, чудом сохранившихся до наших дней. В них они обнаружили упоминание о "старце с козлиной бородой", о необыкновенной теории этого старца, повергшей всё население в ужас, и множество ругани и проклятий, относившихся к несчастному открывателю.
В одном из обрывков было найдено имя Подлезь, которое, вероятно и принадлежало старцу. Открытие его стали называть законом Подлези, который впоследствии трансформировался в Закон Подлости.
Закон Подлости - это закон, устанавливающий прямую зависимость между желанием и неудачным стечением обстоятельств. То есть, можно задать и рассмотреть функцию нескольких переменных. Это аналитическое задание функции.
Подлость вывел формулу зависимости результата от желания и неудачного стечения обстоятельств.
Обозначим желание буквой G, неудачное стечение обстоятельств - No, а результат – Р. К - коэффициент, показывающий степень невезения. Этот коэффициент зачастую зависит от настроения (суперпозиция функций). Чем лучше настроение, тем больше коэффициент К, а следовательно больше желания и лучше результат.
Сфера действия закона
Закон действует везде, независимо от климата, рельефа и других факторов. Действие его охватывает как духовную, так и материальную сферу жизни людей.
Закон действует стихийно. Особенно часто он проявляется, когда желание человека получить что-либо внезапно возрастает, либо же близится к исполнению.
Замечено, что влияние закона на детей во много раз меньше, чем на взрослых людей. Это связано с тем, что человек с возрастом более серьёзно относится к своим проблемам. Он часто настолько загружает себя, что у него пропадают или уменьшаются желания и одновременно находится на низком уровне эмоциональный настрой, что является наиболее благоприятным условием для Подлости.
Несмотря на обширность влияния закона, действие его проявляется далеко не всегда, а зачастую сводится к нулю. Главную роль в этом играет положительный эмоциональный настрой, а так же вера в собственные силы.
Значит, чтобы достигнуть желаемого, необходимо верить в себя и притягивать к себе позитив доброжелательным настроением. Но человеку по многим причинам этого часто недостаёт. Тогда есть два выхода: либо поднять себе настроение и бороться с Подлостью, либо переждать волну собственного пессимизма во избежание отрицательного результата.
6.2. Законы Мерфи
Мерфология (Мерф/и + о + логия/ logos – наука, lego – говорить, собирать) – 1) отрасль знания, посвященная тому, что идет плохо, вкривь, вкось либо не так, как надо; 2) наука об ошибках и неправильных действиях; 3) собирание пословиц, поговорок, афоризмов и иных высказываний в данной области, а также их распространение.
Как появилось название «Закон Мерфи»? В 1949 году на базе Военно-воздушных сил США, расположенной в Мьюроке, Калифорния, велось экспериментальное исследование, посвященное так называемым разрушающим испытаниям и тестированию предельной прочности.
Человеком, в честь которого назван Закон, был капитан Эд Мерфи, инженер-исследователь. Раздасадованный неполадками, вызванными тем, что один из датчиков работал со сбоями и постоянно давал неверные показания из-за ошибки в электрическом монтаже, капитан невольно бросил: «Если существует хоть какой-то способ сделать что-либо неправильно, он обязательно так и сделает», - имея при этом в виду совершенно конкретного техника, который в его лаборатории занимался монтажом. Кто-то включил указанное высказывание в официальный отчет, назвав его Законом Мэрфи…
Спустя некоторое время, руководители проекта указали на пресс-конференции, что своими великолепными результатами, они обязаны твердой вере в Закон Мерфи, а также последовательным и упорным усилиям в борьбе с неизбежным…Так и родился «Закон Мерфи», который стал ни чем иным, как результатам ошибочного цитирования…
Сразу после этого начали появляться все новые и новые "законы Мерфи", не имеющие уже никакого отношения ни к самому капитану Мерфи, ни к проектам ВВС, ни даже к технике вообще. Авторами многих таких "законов" являются весьма известные личности, занимавшие высокие должности. Авторы других так и остались неизвестными.
Однако есть кое-что, что объединяет все эти многочисленные законы Мерфи - они прекрасно объясняют причины, по которым что-либо в вашей жизни или в делах идет не так как надо. Если дела идут вкривь и вкось, то Законы Мерфи помогут стойко переносить превратности судьбы и осознать, что в жизни случается всякое. Потенциал человека в сфере неуместных подозрений, безнадежного остроумия и пессимистической мудрости, безграничен…
Первые главные Законы Мерфи…
1. Если что-то плохое может произойти, оно непременно произойдет.
2. Ничто не бывает таким простым, как кажется вначале.
3. Любое дело занимает больше времени, чем вы думали.
4. Каждое решение порождает новые проблемы
5. Что бы ни произошло плохого, оно, скорее всего, будет потом казаться нормальным
Законов Мерфи достаточно много. Они постоянно «открываются», дорабатываются, дописываются. Я рассмотрела некоторые из них с точки зрения выявления функциональной зависимости и графического изображения.
П
Скорость ветра растет прямо пропорционально стоимости прически
рямая зависимость
Еще законы
Чем меньше делаешь, тем меньше ошибок можешь совершить
Твердость масла прямо пропорциональна мягкости батона
Тот, кто смеется последним, соображает медленнее всех
Чем больше новых законов, тем больше новых лазеек
Разная скорость роста
Продолжительность совещания растет пропорционально квадрату числа присутствующих
Еще законы:
Проблемы разрастаются в геометрической прогрессии, решения – в арифметической.
Друзья приходят и уходят, а вот враги накапливаются
О
Вероятность наступления любого события обратно пропорциональна его желательности
братная
Еще законы
Чем проще идея, тем сложнее ее излагают
Размер доклада о достигнутых результатах обратно пропорционален достигнутым результатам
Чем хуже стрижка, тем медленнее отрастают волосы
Тот, кто живет ближе всех, всегда опаздывает
Чем проще что-то выглядит, тем больше проблем таит
Чем длиннее название должности, тем менее важна связанная с ней работа
Чем короче очередь у кассы, тем медленнее она движется
Неявное задание функции, многозначная функция
Хороший начальник может принимать решения независимо от знания всех фактов
Хороший начальник может принять решение и не имея достаточного количества фактов
Идеальный начальник может руководить, будучи в полном неведении о состоянии дел
«Модуль»
Каждому действию всегда соответствует равная и противоположна направленная критика
Прямая
Если миллион человек верят в какую-то глупость, она все равно останется глупостью
Еще законы:
Любая ошибка в любых расчетах будет стремиться причинить наибольший вред
Сколько бы работы вы ни сделали, этого всегда будет недостаточно
Аналитическое задание функции
Y – усилия, Т – время,
(Если по плану на выполнение работы отведено много времени, первоначальные усилия будут мизерными. По мере того, как остающееся время приближается к нулю, усилия возрастают до бесконечности)
Выполнение первых 90 процентов каждого задания занимает 10 процентов времени, а последние 10 процентов задания занимают оставшиеся 90 процентов времени.
Вывод: и в русских народных пословицах, и в Законе Подлости, и в Законах Мерфи можно найти закономерности, которые могут быть выражены либо аналитическими функциями, либо заданы графически, либо быть наглядно изображены с помощью мощного математического аппарата исследования функций. То есть жизненные закономерности подчиняются правилам математики, что и доказывает мое небольшое исследование.
Заключение:
Казалось бы, математика-это только цифры, которые нужны нам для счёта. Но если внимательнее присмотреться, можно увидеть огромное количество случаев, когда она появляется в нашей жизни не только как сложение и вычитание. Это заставило меня посмотреть на математику чуть глубже. Эта наука, которой уже очень много лет, не перестаёт удивлять нас даже сейчас.
Наблюдая различные процессы и явления, мы стараемся разглядеть самые существенные их черты, самые глубокие закономерности. Часто они оказываются общими для широчайшего круга наблюдаемых событий. Общей оказывается и математическая модель, построенная на основе этих закономерностей.
Функция – это одно из основных общенаучных и математических понятий, выражающее зависимость между переменными величинами.
С функцией на уроках математики я познакомилась в седьмом классе, при изучении темы «Линейные функции». Но, честно сказать, меня тогда эта тема не сильно заинтересовала
Но недавно я начала замечать, что функции встречаются и вокруг нас. И этот интерес привел меня к небольшим исследованиям в области литературы, физики, медицины и юмора…
Однажды я случайно наткнулась на фотоальбом, в котором был указан мой рост за каждый год моей жизни. Я была рада этой находке, потому что никогда не думала, что цифры, сохранённые в мамином альбоме, могут быть такими интересными и облекутся в математическую форму.
Когда я писала сочинение по русскому устному народному творчеству, то появилась идея проследить связь между математикой и литературой. И оказалось, что не зря. Даже в старинных русских пословицах можно увидеть некоторые закономерности!
Жить без юмора в наше время никак нельзя. И оказывается, юмор тоже не обходится без математических функций!
В рамках одной работы невозможно рассмотреть все многообразие окружающих нас функций. Я считаю, что мне удалось показать некоторые примеры нестандартного взгляда на применение математических понятий и функций в окружающей нас жизни.
Нет лучшего чувства на свете, чем то, когда твоя любознательность получает желаемое знание!
Функции живут вокруг нас и с нами, надо только суметь это заметить…
Очень интересно и познавательно - видеть знакомое в незнакомом! Необычное в привычном…
IV. Список использованных источников:
Литература:
1. Бермант А.Ф., Араманович И.Г., «Краткий курс математического анализа для ВТУЗов», Москва, «Наука», главная редакция физико-математической литературы, 1985
2. Блох А. «Законы Мерфи»/ пер. с англ. Е.Г.Гендель, Минск, «Попурри», 2009.
3. Ушакова О.Д. «Пословицы, поговорки и крылатые выражения», С-Петербург , «Литера», 2006
4. Вся физика. Справочник школьника, 7 – 11 класс, Владимир, «Астрель», 2008
5. Пословицы, поговорки, потешки, скороговорки. Пособие для родителей и педагогов./ Сост. Тарабарина Т.И., Елкина Н.В., Ярославль, «Академия развития», 2004
Интернет-ресурсы:
1. Википедия
2. MathUs.ru
3. www.Murphy-law.net
4. www.happydoctor.ru
5. www.dpva.info
6. festival.1september.ru
25
Получите свидетельство
Вход
Проект по математике "Функции вокруг нас. Необычное в привычном" (0.81 MB)
4
16659
1338
мне очень понравилась ваша разработка, Вы молодец!