Примерный вариант переводного экзамена по информатике в 10Б классе (3 часа)
1. Анализ информационных моделей
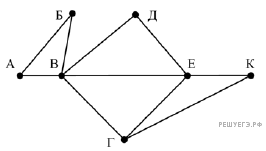
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
|
| П1 | П2 | П3 | П4 | П5 | П6 |
|
| П1 |
| 45 |
| 10 |
|
|
|
| П2 | 45 |
|
| 40 |
| 55 |
|
| П3 |
|
|
|
| 15 | 60 |
|
| П4 | 10 | 40 |
|
|
| 20 | 35 |
| П5 |
|
| 15 |
|
| 55 |
|
| П6 |
| 55 | 60 | 20 | 55 |
| 45 |
| П7 |
|
|
| 35 |
| 45 |
|
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.
Ответ: 20
2.Построение таблиц истинности логических выражений
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| ??? | ??? | ??? | ??? | F |
| 1 |
|
| 1 | 0 |
| 1 |
|
|
| 0 |
|
| 1 |
| 1 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Ответ: ywzx
3. Кодирование и декодирование информации
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0; для буквы Б – кодовое слово 10. Какова наименьшая возможная сумма длин всех шести кодовых слов?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Ответ: 19
4. Кодирование и декодирование информации
Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Закодируйте таким образом последовательность символов ББГА и запишите полученное двоичное число в шестнадцатеричной системе счисления.
Ответ: 5С
5. Передача информации
Документ объёмом 12 Мбайт можно передать с одного компьютера на другой двумя способами:
А) Сжать архиватором, передать архив по каналу связи, распаковать
Б) Передать по каналу связи без использования архиватора.
Какой способ быстрее и насколько, если
• средняя скорость передачи данных по каналу связи составляет 220 бит в секунду,
• объём сжатого архиватором документа равен 25% от исходного,
• время, требуемое на сжатие документа - 22 секунды, на распаковку - 2 секунды?
В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.
Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.
Слов «секунд», «сек.», «с.» к ответу добавлять не нужно.
Ответ: А48
6. Кодирование и декодирование информации. Передача информации (изображение или звук)
Для хранения в информационной системе документы сканируются с разрешением 300 dpi и цветовой системой, содержащей 216 = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 16 Мбайт. В целях экономии было решено перейти на разрешение 150 dpi и цветовую систему, содержащую 256 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Ответ: 2
7. Определение результатов работы простейших алгоритмов.
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси абсцисс, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 6 Направо 150 Вперёд 6 Направо 30]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
О т в е т: 12
8. Перебор слов и системы счисления
Все шестибуквенные слова, составленные из букв К, Л, Н, Т, Э, записаны в алфавитном порядке и пронумерованы, начиная с 1. Начало списка выглядит так:
1. КККККК
2. КККККЛ
3. КККККН
4. КККККТ
5. КККККЭ
...
Под каким номером в списке идёт слово ККЛКЛК?
Ответ: 131
9. Перебор слов и системы счисления
Вася составляет слова из букв слова АВТОРОТА. Код должен состоять из 8 букв, и каждая буква в нём должна встречаться столько же раз, сколько в заданном слове. Кроме того, в коде не должны стоять рядом две гласные и две согласные буквы. Сколько различных слов может составить Вася?
Ответ: 144
10. Вычисление количества информации
 При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 12-символьного набора: А, В, C, D, Е, F, G, H, K, L, M, N. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено целое число байт; это число одно и то же для всех пользователей. Для хранения сведений о 20 пользователях потребовалось 400 байт. Сколько байт выделено для хранения дополнительных сведений об одном пользователе? В ответе запишите только целое число — количество байт.
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 12-символьного набора: А, В, C, D, Е, F, G, H, K, L, M, N. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено целое число байт; это число одно и то же для всех пользователей. Для хранения сведений о 20 пользователях потребовалось 400 байт. Сколько байт выделено для хранения дополнительных сведений об одном пользователе? В ответе запишите только целое число — количество байт.
Ответ: 12
11. Поиск путей в графе
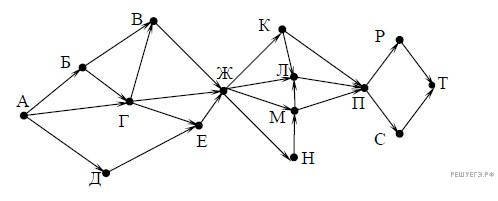
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П, Р, С, Т. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город Т, проходящих через город Н?
Ответ: 32
12. Кодирование чисел. Системы счисления
Значение выражения 496 · 719 − 79 − 21 записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи?
Ответ: 28
13. Кодирование чисел. Системы счисления
Операнды арифметического выражения записаны в системе счисления с основанием 17:
9759x₁₇ + 3x108₁₇
В записи чисел переменной x обозначена неизвестная цифра из алфавита 17-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Ответ: 95306
14. Преобразование логических выражений
Сколько существует целых значений числа A, при которых формула
((x A) → (x2 ∧ ((y2 ≤ 64) → (y ≤ A))
тождественно истинна при любых целых неотрицательных x и y?
Ответ: 3
15. Преобразование логических выражений
На числовой прямой даны два отрезка: P = [130; 171] и Q = [150; 185]. Укажите наименьшую возможную длину такого отрезка A, что формула
(x ∈ P) → (((x ∈ Q) ∧ ¬(x ∈ A)) → ¬(x ∈ P))
истинна при любом значении переменной х, т. е. принимает значение 1 при любом значении переменной х.
Ответ: 21
16. Запросы для поисковых систем с использованием логических выражений
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
| Запрос | Найдено страниц |
| Евклид & Аристотель & Платон | 120 |
| Евклид & Платон | 280 |
| Евклид & Аристотель | 780 |
Компьютер печатает количество страниц (в тысячах), которое будет найдено по следующему запросу: Евклид & (Аристотель|Платон) Укажите целое число, которое напечатает компьютер. Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Ответ: 940
17. Рекурсивные алгоритмы. (2 балла)
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(n) = n при n ≤ 2;
F(n) = F(n − 1) + 2×F(n − 2) при n 2.
Чему равно значение функции F(6)? В ответе запишите только натуральное число.
Ответ: 32
18. Обработки числовой последовательности. Задача решается с использованием прилагающегося файла с данными. (2 балла)
В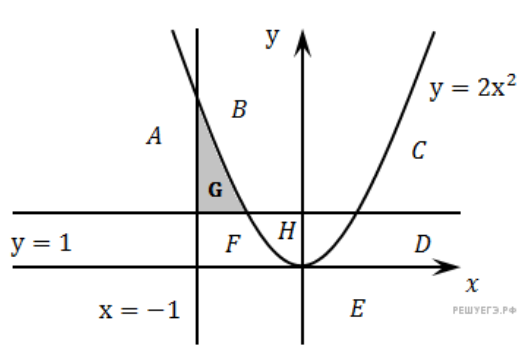 файле 18.txt содержится последовательность целых чисел. Элементы последовательности могут принимать значения от –100 до 100 включительно. Определите сначала количество пар элементов последовательности, в которых хотя бы одно число оканчивается на 7, а затем максимальную из сумм элементов таких пар. Под парой подразумевается два идущих подряд элемента последовательности. Например, для последовательности из 5 элементов: 7, 27, 17, 5, 57 ответ должен быть 4 62.
файле 18.txt содержится последовательность целых чисел. Элементы последовательности могут принимать значения от –100 до 100 включительно. Определите сначала количество пар элементов последовательности, в которых хотя бы одно число оканчивается на 7, а затем максимальную из сумм элементов таких пар. Под парой подразумевается два идущих подряд элемента последовательности. Например, для последовательности из 5 элементов: 7, 27, 17, 5, 57 ответ должен быть 4 62.
Ответ: 16 159
19. Поиск и исправление ошибок в программе с координатной плоскостью. (2 балла)
Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (х, у — действительные числа) и определяет принадлежность точки заштрихованной области. Программист торопился и написал программу неправильно.
x = float(input())
y = float(input())
if у
if x = -1:
if у = 1:
print("принадлежит")
else:
print("не принадлежит")
Укажите координаты точки, в которой программа будет работать неверно.
Укажите, как нужно доработать программу, чтобы не было случаев её неправильной работы. (Это можно сделать несколькими способами, достаточно указать любой способ доработки исходной программы.)
Ответ: Например (2,7). м/б другие
if (у = −1) and (у = 1) and (х
print ('принадлежит')
else
print ('не принадлежит')
(могут быть и другие способы доработки).
20. Поиск и исправление ошибок в вычислительной программе. (2 балла)
На вход программы поступает натуральное число N, не превышающее 109. Требуется найти и наибольшую нечётную цифру в десятичной записи этого числа или вывести «NO», если таких цифр нет. К сожалению, приведённая ниже программа неправильная.
N = int(input())
t = 0
m = t
while N 1:
d = N % 10
if d % 2 == 1 or d m:
m = d
N = N // 10
if m == t:
print("NO")
else:
print(m)
Последовательно выполните следующее.
1. Какое наименьшее число может быть выведено при работе этой программы? Приведите пример числа N, при вводе которого программа выведет такой ответ.
2. Найдите допущенные программистом ошибки и исправьте их.
Ответ: 1, например, при вводе числа 11.
В программе нужно исправить две ошибки
Было: while N 1 Исправление: while N 0
Было: if (d % 2 == 1) or (d m): Исправление: if (d % 2 = 1) and (d m):
21. Поиск символов в текстовом редакторе (файл 21.docx прилагается)
С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «долг» или «Долг» в тексте романа в стихах А. С. Пушкина «Евгений Онегин». Другие формы слова «долг», такие как «долги», «долгами» и т. д., учитывать не следует. В ответе укажите только число.
Ответ: 1.
22. Выигрышная стратегия.
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня либо увеличить количество камней в куче в пять раз. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 75 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 68.
Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу, в которой будет 68 или больше камней. В начальный момент в куче было S камней; 1 ≤ S ≤ 67.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Ответ: 3
23. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
Ответ: 9 12
17.
24. Выигрышная стратегия.
Ответ: 8.
9

 Получите свидетельство
Получите свидетельство Вход
Вход



 П7
П7








 Примерный вариант входного теста по информатике для 11 класса (140.08 KB)
Примерный вариант входного теста по информатике для 11 класса (140.08 KB)
 0
0 144
144 7
7 Нравится
0
Нравится
0


