
Приёмы развития смыслового чтения на уроках математики
Классификация текстов
Художественные
По содержанию
Нехудожественные

Виды работы с текстом на уроках математики
- Работа с объяснительным текстом учебника
- Решение текстовых задач (краткая запись условия задачи)

Работа с текстом учебника

Игра «Попробуй найти!»
В ходе игры учитель сообщают классу название главы или параграфа.
Ученики должны быстро с помощью оглавления найти данный раздел учебника и зачитать несколько строк из него.

«Банк идей (гипотез)»
Куда ученики «складывают» свои мысли о том, что будет сегодня на уроке изучаться.
Учитель при этом вывешивает заготовленные записи высказываний учеников на доску (или записывает), чтобы в конце урока проверить, верны или нет, были выдвинутые ими гипотезы.

Верю – не верю
Учащиеся, выбирая “верные утверждения” из предложенных учителем, описывают заданную тему (ситуацию, обстановку, систему правил).
В 5 классе Тема «Углы».
- Тупой угол – это угол, который нарисован тупым карандашом
- Угол – это геометрическая фигура.
- Угол состоит из двух пресекающихся прямых
- Бывают углы остроумные и тупые
- Угол состоит из двух лучей, выходящих из одной точки
- Равные углы – это те, у которых равны стороны
- Биссектриса – это такой угол, у которого три стороны.
- Бывает угол прямой
- Угол может быть тощим
- Острый угол – это угол, который меньше прямого

Способы обработки информации
Технологический прием “Инсерт” и таблица “Инсерт” сделают зримыми процесс накопления информации, путь от “старого” знания к “новому”
Знак
Значение знака
V
отмечается в тексте информация, которая уже известна ученику
+
отмечается новое знание, новая информация
―
отмечается то, что идет вразрез с имеющимися у ученика представлениями, о чем он думал иначе
?
отмечается то, что осталось непонятным и требует дополнительных сведений, вызывает желание узнать подробнее
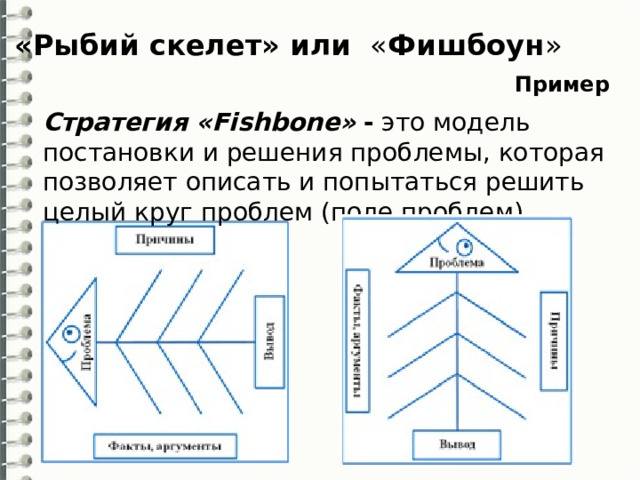
«Рыбий скелет» или « Фишбоун »
Пример
Стратегия «Fishbone» - это модель постановки и решения проблемы, которая позволяет описать и попытаться решить целый круг проблем (поле проблем).
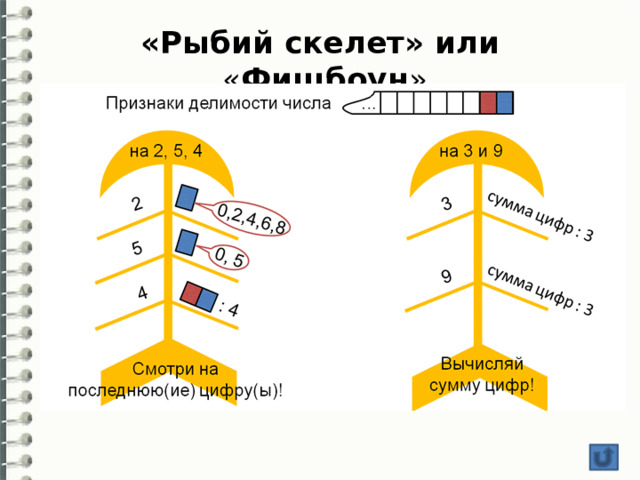
«Рыбий скелет» или « Фишбоун »

План и тезисы на примере одного и того же текста из учебника математики для 5 класса «Угол».
Тезисы.
План.
- 1. Понятие угла.
- 2. Равные углы.
- 3. Развёрнутый угол.
- 4. Прямой угол.
1. Углом называют фигуру, образованную двумя лучами, выходящими из одной точки. Лучи, образующие угол, называют сторонами угла, а точку, из которой они выходят,- вершиной угла.
2. Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
3. Два дополнительных друг другу луча образуют развёрнутый угол. Стороны этого угла вместе образуют прямую линию, на которой лежит вершина развёрнутого угла.
4. Прямым углом называют половину развёрнутого угла.
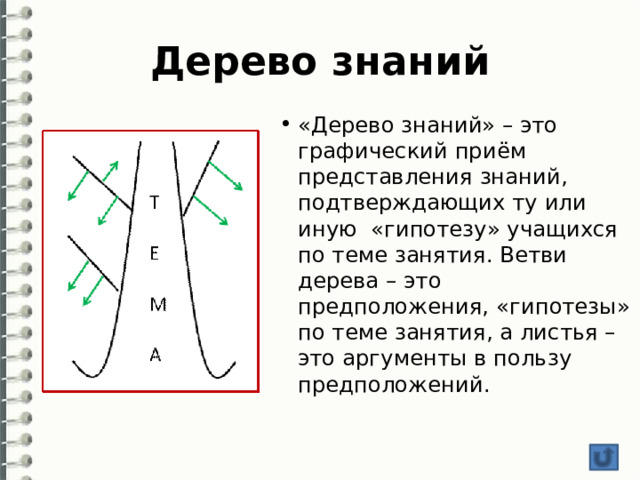
Дерево знаний
- «Дерево знаний» – это графический приём представления знаний, подтверждающих ту или иную «гипотезу» учащихся по теме занятия. Ветви дерева – это предположения, «гипотезы» по теме занятия, а листья – это аргументы в пользу предположений.

Кластер
Пример1
Пример2
Термин «кластер» происходит от английского «cluster» – гроздь, скопление.
При построении кластера
в центральном овале располагают ключевое понятие;
в овалах второго уровня – понятия, раскрывающие смысл ключевого;
в овалах третьего уровня идет детализация понятий, упомянутых на предыдущем уровне.
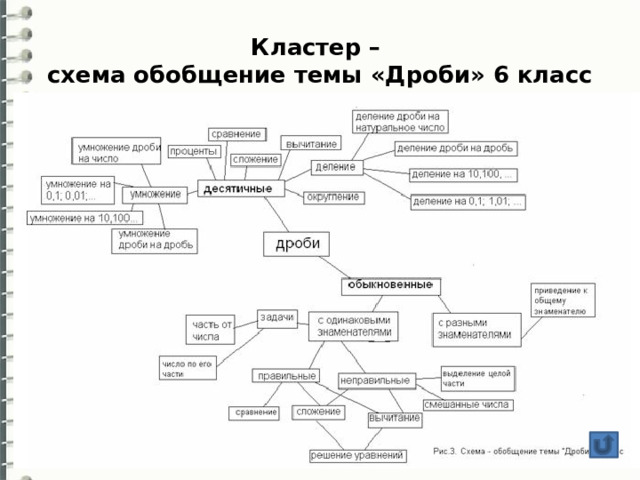
Кластер – схема обобщение темы «Дроби» 6 класс
 0, тупой угол при kГрафики двух функций пересекаются, если k 1 ≠k 2 Графики двух функций параллельны, если k 1 =k 2 " width="640"
0, тупой угол при kГрафики двух функций пересекаются, если k 1 ≠k 2 Графики двух функций параллельны, если k 1 =k 2 " width="640"
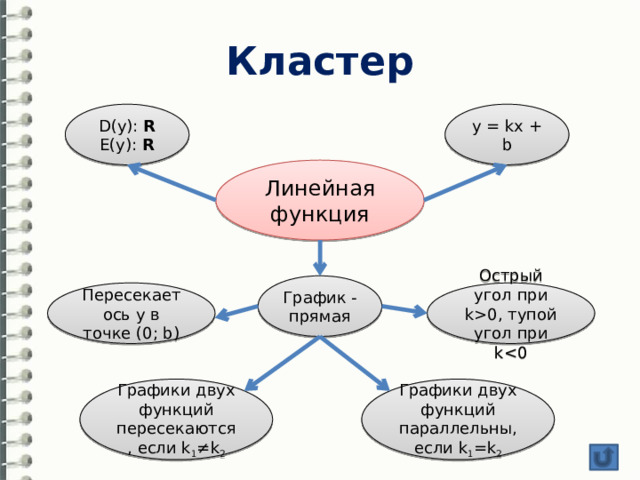
Кластер
y = kx + b
D(y): R
E(y): R
Линейная функция
График - прямая
Пересекает ось y в точке (0; b)
Острый угол при k0, тупой угол при k
Графики двух функций пересекаются, если k 1 ≠k 2
Графики двух функций параллельны, если k 1 =k 2

Денотатный граф
пример
Денотатный граф (от лат. denoto — обозначаю) — очень эффективный способ вычленения из текста существенных признаков ключевого понятия.
Правила построения:
- Выделите ключевое понятие (слово или словосочетание) и проанализируйте его существенные признаки. Впишите ключевое понятие в верхний прямоугольник.
- Как можно более точно подберите глаголы, связывающие ключевое понятие и его существенные признаки , отражающие движение от понятия к его существенным признакам. Это могут быть самые разнообразные глаголы-связки, с помощью которых осуществляется выход на определение понятия. Впишите глаголы в прямоугольники второго уровня.
- Конкретизируйте в прямоугольниках следующего уровня смысл выбранных вами глаголов для более полного раскрытия ключевого понятия.
- Следите за чередованием имени (именем может быть одно существительное или группа существительных в сочетании с другими именными частями речи) и глагола .
- Проверяйте каждый блок включенной в граф информации
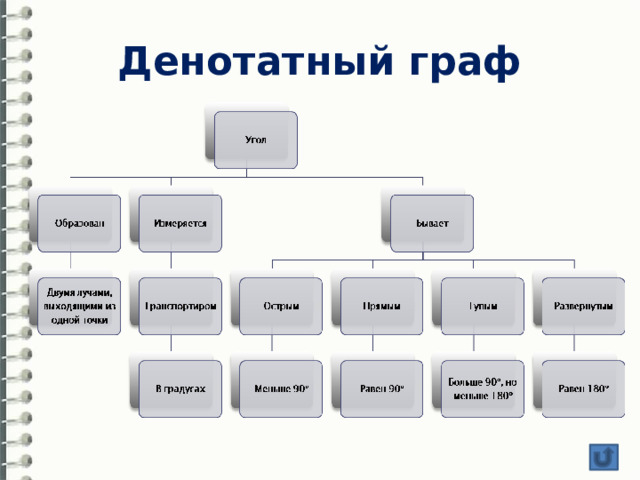
Денотатный граф
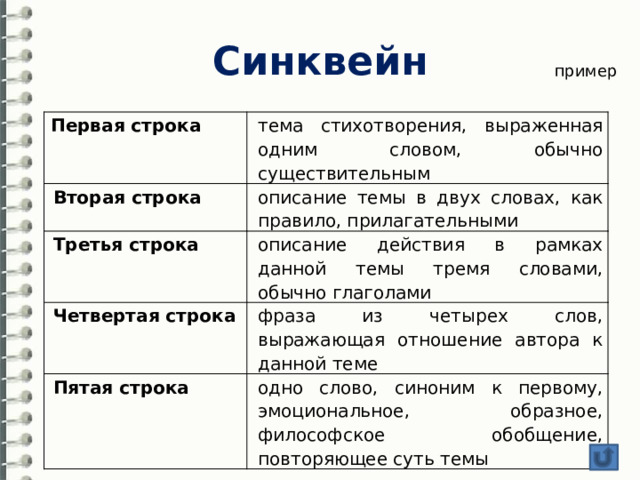
Синквейн
пример
Первая строка
тема стихотворения, выраженная одним словом, обычно существительным
Вторая строка
описание темы в двух словах, как правило, прилагательными
Третья строка
описание действия в рамках данной темы тремя словами, обычно глаголами
Четвертая строка
фраза из четырех слов, выражающая отношение автора к данной теме
Пятая строка
одно слово, синоним к первому, эмоциональное, образное, философское обобщение, повторяющее суть темы

Кубик Блума (Ромашка Блума)
На гранях кубика написаны начала вопросов:
«Почему»,
«Объясни»,
«Назови»,
«Предложи»,
«Придумай»,
«Поделись»
Учитель (или ученик) бросает кубик. Необходимо сформулировать вопрос к учебному материалу по той грани, на которую выпадет кубик

Краткая запись условия задачи
- Схема
- Ключевые слова с указанием связей
- Таблица
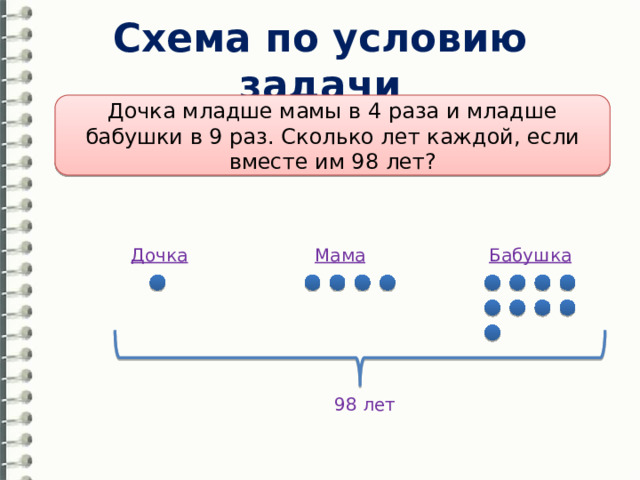
Схема по условию задачи
Дочка младше мамы в 4 раза и младше бабушки в 9 раз. Сколько лет каждой, если вместе им 98 лет?
Дочка
Бабушка
Мама
98 лет
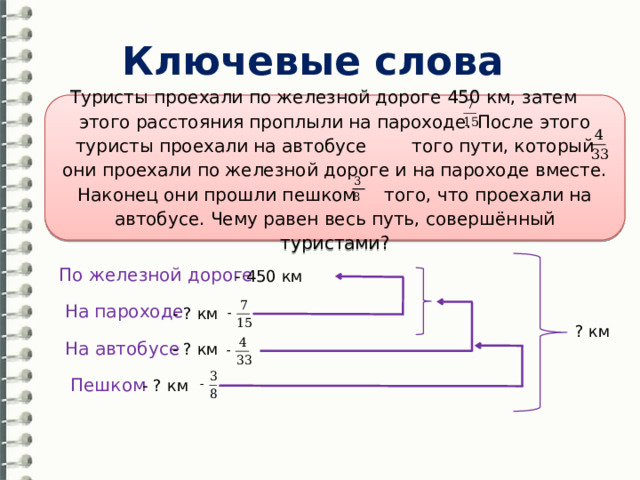
Ключевые слова
Туристы проехали по железной дороге 450 км, затем этого расстояния проплыли на пароходе. После этого туристы проехали на автобусе того пути, который они проехали по железной дороге и на пароходе вместе. Наконец они прошли пешком того, что проехали на автобусе. Чему равен весь путь, совершённый туристами?
По железной дороге
- 450 км
На пароходе
- ? км
? км
На автобусе
- ? км
Пешком
- ? км

Таблица
Два автомата должны были изготовить по 240 деталей. Первый автомат изготавливал в час на 5 деталей больше, чем второй, и поэтому закончил работу на 4 часа раньше. Сколько деталей изготавливал в час каждый автомат?
A = p t
A
p
t
240 дет.
(x + 5) дет.
I автомат
240 дет.
х дет.
I I автомат

Таблица
Мотоциклист проехал 40 км от дома до реки. Возвращаясь обратно со скоростью на 10 км/ч меньше первоначальной, он затратил на этот путь на 20 минут больше. Какова была первоначальная скорость мотоциклиста?
S = v t
S
v
t
40 км
х км/ч
Вперёд
40 км
(х – 10) км/ч
Обратно

ПРИМЕРЫ СИНКВЕЙНА
Прямые. Пересекающиеся, параллельные. Строим, переносим, совмещаем. Нет ни начала, ни конца?! Бесконечность!
Масштаб
Численный, именованный
Делить, находить, вычислять
Дробь, которую нужно понять
Отношение.

МНЕМОНИЧЕСКИЕ ПРАВИЛА (примеры)
- Число
3 1 4 1 5 9
Это я знаю и помню прекрасно:
2 6 5 3 5 8
Пи - многие знаки тут лишни, напрасны .
Число букв в каждом слове дает соответствующую цифру в десятичном представлении числа 3,14159265358

МНЕМОНИЧЕСКИЕ ПРАВИЛА (примеры)
22/7 .
Открыл это приближение древнегреческий математик Архимед. Чтобы запомнить это отношение есть строчки:
Двадцать две совы мечтали
О семи больших мышах.

МНЕМОНИЧЕСКИЕ ПРАВИЛА (примеры)
Число е
Чтобы запомнить значение этого иррационального числа используется следующая фраза:
Способ помнить е простой:
Два, семь, дважды Лев Толстой,
И углы равнобедренного прямоугольного треугольника.
е 2,7 1828 1828 45 90 45
где 1828 – год рождения Л. Н. Толстого,
45°, 90°, 45° - углы равнобедренного прямоугольного треугольника.
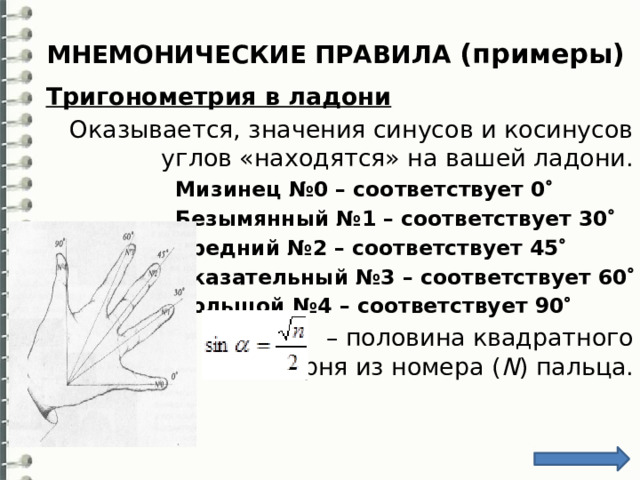
МНЕМОНИЧЕСКИЕ ПРАВИЛА (примеры)
Тригонометрия в ладони
Оказывается, значения синусов и косинусов углов «находятся» на вашей ладони.
Мизинец №0 – соответствует 0
Безымянный №1 – соответствует 30
Средний №2 – соответствует 45
Указательный №3 – соответствует 60
Большой №4 – соответствует 90
– половина квадратного корня из номера ( N ) пальца.

МНЕМОНИЧЕСКИЕ ПРАВИЛА (примеры)
Тригонометрия в ладони
.

МНЕМОНИЧЕСКИЕ ПРАВИЛА (примеры)
Римские цифры
М=1000, D=500, С=100, L=50,
X=10,V=5, I=1
М ы Д арим С очные Л имоны,
Х ватит В сем И ещё останется .
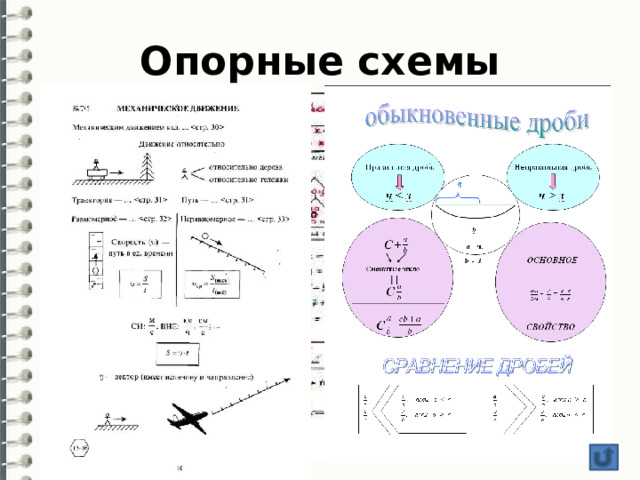
Опорные схемы
Интерактивные приёмы работы с текстом учебника
Обеспечивают усвоение учебного материала
Активизируют умственную деятельность учащихся
Прививают интерес к изучаемому предмету

Учителю необходимо:
- выбирать наиболее рациональные виды чтения для усвоения учащимися нового материала;
- формировать у учащихся интерес к чтению через внедрение нестандартных форм и методов работы с текстом;
- определять характер деятельности различных групп
учащихся при работе с учебником;
- предвидеть возможные затруднения учащихся в тех или иных видах учебной деятельности;
- повышать уровень самостоятельности учащихся в чтении по мере их продвижения вперед;
- организовывать различные виды деятельности учащихся с целью развития у них творческого мышления;
- обучать самоконтролю и самоорганизации в различных видах деятельности.

Спасибо за внимание

 Получите свидетельство
Получите свидетельство Вход
Вход












 Приёмы развития смыслового чтения на уроках математики (1.79 MB)
Приёмы развития смыслового чтения на уроках математики (1.79 MB)
 0
0 235
235 3
3 Нравится
0
Нравится
0



