Презентация "Золотое сечение"

ЗОЛОТОЕ СЕЧЕНИЕ

МОУ «Ягницкая школа»

Сёмкина Полина

7 класс

Руководитель:

Н.А. Долбилова

учитель математики

Цель: изучить теоритический материал по теме «Золотое сечение», рассмотреть применение понятия «божественная пропорция» в математике, искусстве, природе.

Задачи:

• дать определение «золотого сечения», показать его алгебраическое нахождение и геометрическое построение;
• выяснить, что такое «золотые фигуры», эталонная модель гармонически развитого тела человека;
• совершенствовать умения по применению знаний и способов действий в измененных и новых учебных ситуациях.

Методы исследования: работа с литературными источниками, обработка и систематизация информации.

• Слово «пропорция» (от латинского proportio) означает «соразмерность», «определённое соотношение частей между собой»

• Учение о пропорциях особенно успешно развивалось в IV в. до н. э. в Древней Греции

• С пропорциями связывались представления о красоте, порядке и гармонии

Пропорции

В математике пропорцией называют

равенство двух отношений: a : b = c : d

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему .

a : b = b : c или с : b = b : а

Термин "ЗОЛОТОЕ СЕЧЕНИЕ" ввёл Леонардо да Винчи (конец 15 - начало 16 вв.). Принципы золотого сечения или близкие ему пропорциональные отношения легли в основу композиционного построения многих произведений мирового искусства (главным образом произведений архитектуры античности и Возрождения).

Числа Фибоначчи

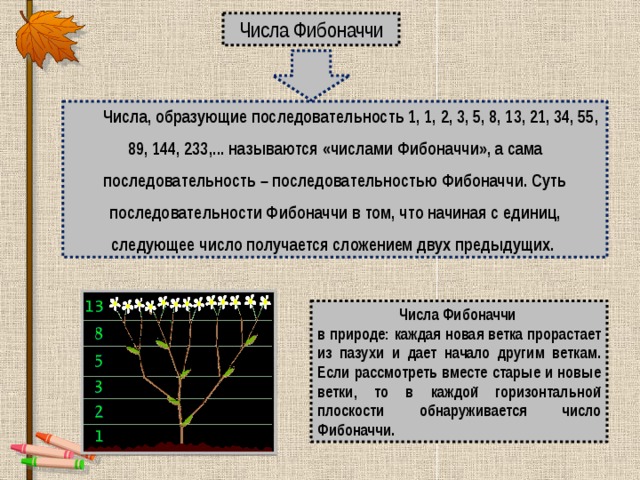
Числа, образующие последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,... называются «числами Фибоначчи», а сама последовательность – последовательностью Фибоначчи. Суть последовательности Фибоначчи в том, что начиная с единиц, следующее число получается сложением двух предыдущих.

Числа Фибоначчи

в природе: каждая новая ветка прорастает из пазухи и дает начало другим веткам. Если рассмотреть вместе старые и новые ветки, то в каждой горизонтальной плоскости обнаруживается число Фибоначчи.

Золотой прямоугольник

Прямоугольник с «золотым» отношением сторон стали называть «золотым прямоугольником. Он обладает интересным свойством. Если от него отрезать квадрат, то останется вновь золотой прямоугольник. Этот процесс можно продолжать до бесконечности.

Золотой треугольник

«Золотой треугольник» – это равнобедренный треугольник, у которого отношение длины основания к длине боковой стороны равняется 0,618.

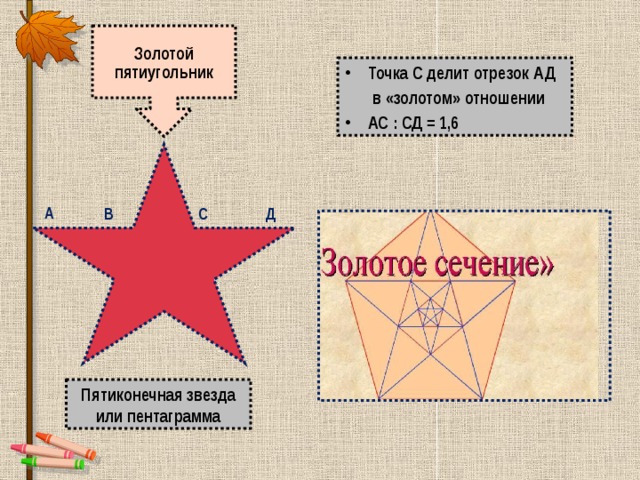
Золотой пятиугольник

• Точка С делит отрезок АД

в «золотом» отношении

• АС : СД = 1,6

А

В

С

Д

Пятиконечная звезда или пентаграмма

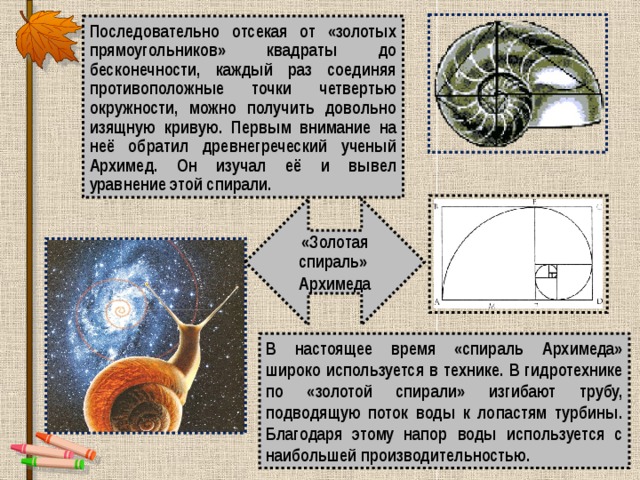
Последовательно отсекая от «золотых прямоугольников» квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, можно получить довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед. Он изучал её и вывел уравнение этой спирали.

«Золотая спираль»

Архимеда

В настоящее время «спираль Архимеда» широко используется в технике. В гидротехнике по «золотой спирали» изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды используется с наибольшей производительностью.

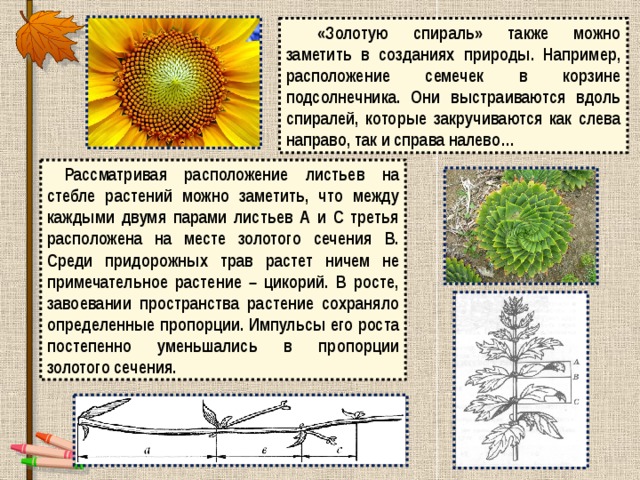
«Золотую спираль» также можно заметить в созданиях природы. Например, расположение семечек в корзине подсолнечника. Они выстраиваются вдоль спиралей, которые закручиваются как слева направо, так и справа налево…

Рассматривая расположение листьев на стебле растений можно заметить, что между каждыми двумя парами листьев А и С третья расположена на месте золотого сечения В. Среди придорожных трав растет ничем не примечательное растение – цикорий. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Однако есть предположение, что первыми к принципу золотого сечения пришли все же египтяне.

Наиболее известная пирамида Хеопса

построена с использованием, так

называемого золотого треугольника, в

котором соотношение гипотенузы к

меньшему катету равно золотому

сечению. Храмы, барельефы, предметы

быта, украшения из гробницы Тутанхамона

свидетельствуют, что египетские мастера

пользовались соотношениями золотого

деления при их создании.

Говоря о примерах «золотого сечения», нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в.

Портрет Моны Лизы (Джоконды) работы Леонардо да Винчи долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, т.е. с использованием «золотого сечения».

Витрувианский человек

Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники. Именно Леонардо да Винчи, пользуясь «золотым сечением», создал учение об идеальных пропорциях человеческого тела.

Модулор — система пропорций, предложенная Ле Корбюзье в 1940-х годах. Основу Модулора составляют: размеры и пропорции человеческого тела — за исходные величины взят условный рост человека, его высота до солнечного сплетения и с поднятой рукой приняты равными 183, 113 и 226 см, золотое сечение, ряд чисел Фибоначчи.

Немецкий ученый Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил «золотому сечению». Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный циркуль Дюрера.

Великий древнегреческий

скульптор Фидий часто

использовал «золотое

сечение» в своих

произведениях. Его статуя

Зевса Олимпийского,

считалась одним из чудес

света.

Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление совершенства целого и его частей в искусстве, науке, технике и природе.

Греческий скульптор Леохар создал знаменитую статую Аполлона Бельведерского, воплотившую представление древних греков о красоте.

Статуя Афины Парфенос дала название Парфенону – одному из самых величественных храмов Древней Греции. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

Афина Парфенос - всемирно известная статуя Фидия, созданная по законам «божественной пропорции».

Золотое сечение

в анатомии, биологии

Золотое сечение

в архитектуре

Золотое сечение в картине И.И. Шишкина «Сосновая роща»

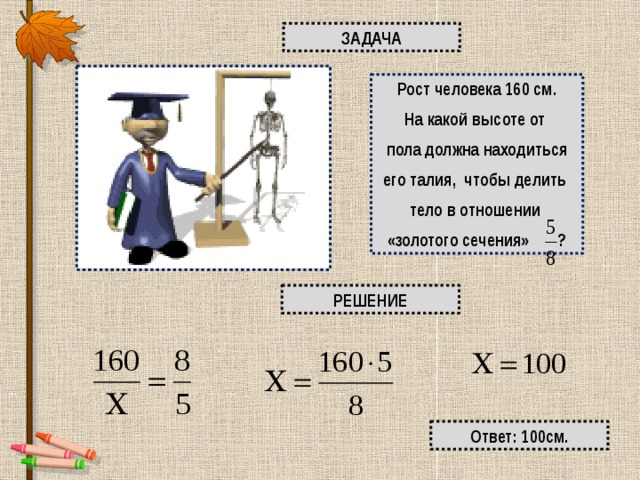
ЗАДАЧА

Рост человека 160 см.

На какой высоте от

пола должна находиться

его талия, чтобы делить

тело в отношении

«золотого сечения» ?

РЕШЕНИЕ

Ответ: 100см.

ЗАДАЧА

С давних времён размеры книг

находились в отношении «золотого сечения» (примерно ).

Найдите ширину учебника Геометрия 7, если её длина равна 17 см.

Ответ: ширина учебника Геометрия 7

27,2 см.

Выводы:

• золотое сечение – это один из основополагающих принципов природы;
• человеческое представление о красоте явно сформировалось под влиянием того, какой порядок и гармонию человек видит в природе;
• несмотря на неприятие «золотого сечения» современными «официальными науками, оно повсеместно используется в технике, во многих странах мира, в том числе в России.

Геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением. И если первое из этих двух сокровищ можно сравнить с мерой золота, то второе с драгоценным камнем. Теорему Пифагора знает каждый школьник, а что такое золотое сечение - далеко не все.

Иоганн Кеплер