Презентация "Векторы и их применение"

Векторы и их применение

Максименко Н.В., преподаватель математики

Нет ни одной области математики, как бы абстрактна она ни была, которая когда-нибудь не окажется применимой к явлениям действительного мира

Николай Иванович Лобачевский

Цель занятия

Обобщение ранее изученного материала по теме «Векторы в пространстве» и выявление уровня усвоения навыков применения знаний о векторах в пространстве при решении задач по математике и физике

План работы

• Применение векторов в различных областях
• Актуализация знаний
• Решение задач по математике и физике
• Практическая работа
• Рефлексия
• Домашнее задание

Понятие «Вектор»

Герман Грассман Уильям Гамильтон

(немецкий математик) (ирландский математик и астроном)

Современная символика для обозначения вектора

Барон Огюстен-Луи Коши

(французский математик)

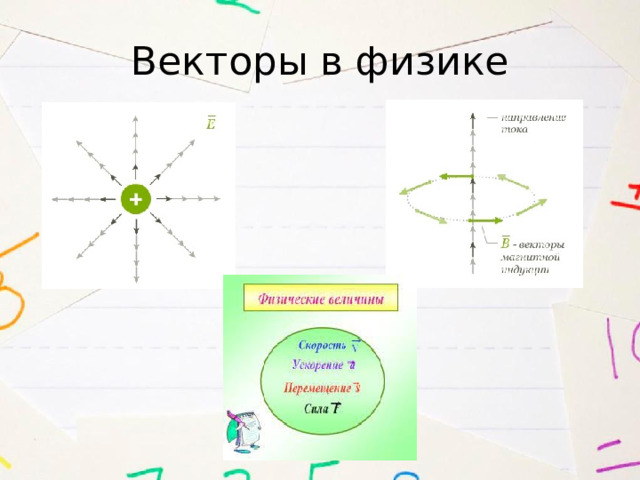
Векторы в физике

Системно-векторная психология

Векторы в повседневной жизни

Выводы:

• Каждый человек постоянно сталкивается с векторами в повседневной жизни
• Векторы необходимы нам для изучения не только математики, но и других наук
• Векторы — мощный инструмент математики и физики. На языке векторов формулируются основные законы механики и электродинамики
• Каждый должен знать, что такое вектор

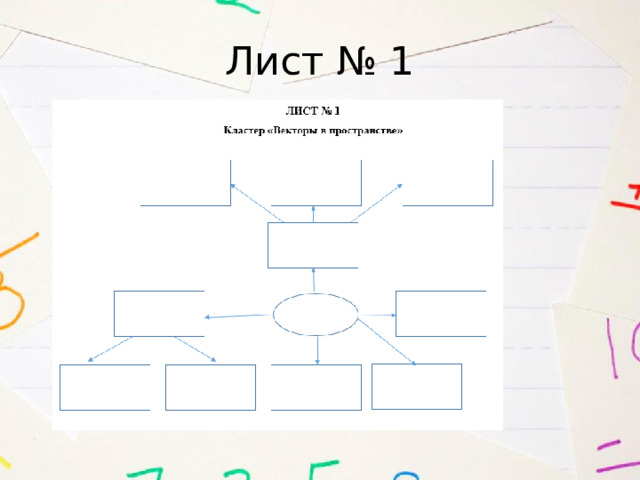
Лист № 1

Работа с кластером

• 1) Величина, которая задается своей длиной и направлением, называется …?
• Вектором
• 2) Любая точка пространства может рассматриваться как вектор. Такой вектор называется … ?
• (Нулевым)
• 3) Два ненулевых вектора, которые лежат на одной прямой или на параллельных прямых, называются …?
• ( Коллинеарными )

Работа с кластером

• 4) Коллинеарные векторы, имеющие одно направление, называются …?
• (Сонаправленными)
• 5) Коллинеарные векторы, имеющие разные направление, называются …?
• (Противоположно направленными)
• 6) Длиной ненулевого вектора называется …?
• (Длина отрезка АВ)

Работа с кластером

• 7) Даны два вектора и . Если данные векторы отложить последовательно друг за другом (начало вектора попадает в конец вектора ), то вектор суммы соединяет начало одного вектора с концом второго вектора. Такой приём сложения векторов называется …?
• (Правилом треугольника)

Работа с кластером

• 8) Величины, которые характеризуются числовым значением и направлением, называются …?
• (Векторными или векторами)
• 9) Примерами векторных величин из курса физики являются … .
• (Скорость, ускорение, сила)

Интеллектуальная разминка

• Назовите пары сонаправленных векторов
• ()
• Назовите пары противоположно направленных векторов
• ()

Интеллектуальная разминка

• Назовите пары равных векторов
• ()
• Назовите пары, не являющиеся ни сонаправленными,

ни противоположно

направленными

• ()

Понятие вектора в физике и математике

В математике

В математике

В физике

Изучаем векторы , и

В физике

Изучаем векторные величины , и

Вектор можно отложить от любой точки плоскости

Вектор можно отложить от любой точки плоскости

Вектор имеет точку приложения (на теле)

Правила сложения векторов: Правило треугольника и правило параллелограмма

Вектор имеет точку приложения (на теле)

Правила сложения векторов: Правило треугольника и правило параллелограмма

Правила сложения векторов: Правило треугольника и правило параллелограмма (чаще применяем правило параллелограмма)

Правила сложения векторов: Правило треугольника и правило параллелограмма (чаще применяем правило параллелограмма)

Длину вектора называем модулем

Длину вектора называем модулем

Длину вектора называем длиной

Длину вектора называем длиной

Лист № 2

Задача № 1

Дан тетраэдр ABCD. Докажите, что

Решение:

• По правилу треугольника найдём
• По правилу треугольника найдём
• Сравним получившиеся в результате сложения векторы. Если получатся равные векторы, то утверждение будет доказано

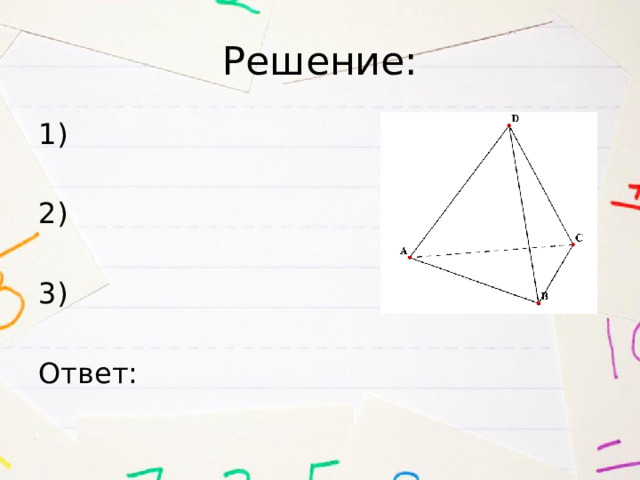
Решение:

1)

2)

3)

Ответ:

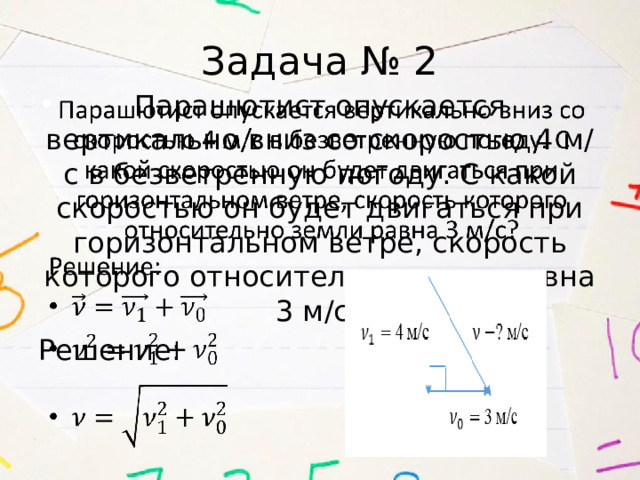
Задача № 2

Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно земли равна 3 м/с?

Решение:

Решение:

• Ответ:

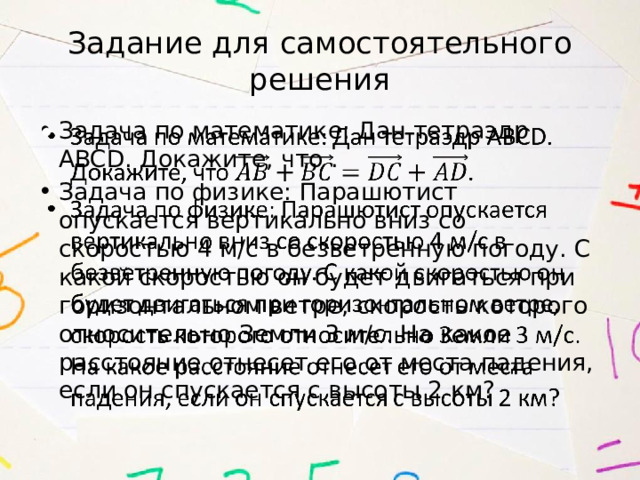
Задание для самостоятельного решения

• Задача по математике: Дан тетраэдр ABCD. Докажите, что .
• Задача по физике: Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно Земли 3 м/с. На какое расстояние отнесет его от места падения, если он спускается с высоты 2 км?

Эталоны ответа

• Задача № 1.

• Задача № 2.

Критерии оценки

• «5» - задание выполнено без ошибок
• «4» - задание выполнено с 1-2 ошибками
• «3» - задание выполнено с 3-4 ошибками

Лист № 3

Лист № 4

Рефлексия

На занятии я работал

активно / пассивно

Своей работой на занятии я

доволен / не доволен

Занятие для меня показалось

коротким / длинным

За занятие я

не устал / устал

Моё настроение

стало лучше / стало хуже

Материал занятия мне был

понятен / не понятен

Цель занятия

Обобщение ранее изученного материала по теме «Векторы в пространстве» и выявление уровня усвоения навыков применения знаний о векторах в пространстве при решении задач по математике и физике