Презентация по теории вероятностей

МБОУ «Лицей №1 им. академика Б.Н.Петрова»

«Элементы теории вероятностей при подготовке к итоговой аттестации»

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Подготовила: Рябович С.В,

учитель математики

Задачи на классическое определение вероятности

• В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике.

Решение:

11 вопросов – это число благоприятных исходов;

55 вопросов – это общее число исходов.

Тогда вероятность определяем следующим образом:

P(A) = 11/55;

P(A) = 0,2.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

2

Задачи на классическое определение вероятности

2. В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Решение:

1000-5 = 995 насосов – это число благоприятных исходов;

1000 насосов – это общее число исходов.

Тогда вероятность определяем следующим образом:

P(A) = 995/1000;

P(A) = 0,995.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

3

Задачи на классическое определение вероятности

3. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

Решение:

100 сумок – это число благоприятных исходов;

100+8 = 108 – это общее число исходов.

Тогда вероятность определяем следующим образом:

P(A) = 100/108;

P(A) = 0,9259 ≈ 0,93 .

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

4

Задачи на классическое определение вероятности

4. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.

Решение:

12+18 = 30 мест – это число благоприятных исходов;

300 – это общее число исходов.

Тогда вероятность равна P(A) = 30/300;

P(A) = 0,1.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

5

Задачи на классическое определение вероятности

5. В группе туристов 30 человек. Их вертолётом забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.

Решение:

6 человек – это число благоприятных исходов;

30 – это общее число исходов.

Тогда вероятность определяем следующим образом:

P(A) = 6/30;

P(A) = 0,2.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

6

Задачи на классическое определение вероятности

6. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?

Решение:

Поскольку один участник из России уже определен, то нужно найти вероятность выбора еще одного участника из России, а значит, Р = 9/25 = 0,36.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

7

Задачи на классическое определение вероятности

7. В ящике находятся черные и белые шары, причем черных в 4 раза больше, чем белых. Из ящика случайным образом достали один шар. Найдите вероятность того, что он белый.

Решение:

Пусть х–число белых шаров, 4х–число черных шаров.

Тогда х - это число благоприятных исходов;

х+4х = 5х – это общее число исходов.

Значит вероятность равна:

P(A) = х/5х;

P(A) = 0,2.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

8

Задачи на классическое определение вероятности

8. Андрей выбирает случайное трехзначное число. Найдите вероятность того, что оно делится на 33.

Решение:

Необходимо узнать количество трехзначных чисел, делящихся на 33.

а 1 = 132, а n = 990 ; 990 = 132 + 33 ∙ ( n – 1); n = 27.

Значит, 27 – это число благоприятных исходов;

900 – это общее число исходов.

Тогда вероятность равна

P(A) = 27/900;

P(A) = 0,03.

Значит вероятно5сть равна:

P(A) = х/5х;

P(A) = 0,2.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

9

Задача на противоположные события

9. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

Решение:

События А: ручка пишет хорошо и В: ручка пишет плохо являются противоположными, поэтому сумма их вероятностей равна единице, т.е.

P(A) + Р(В)= 1.

Следовательно, искомая вероятность равна

P(A) = 1 - 0,19 = 0,81.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

10

Задачи на кубики

10. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?

Решение:

Благоприятствуют событию только такие исходы, когда выпадет грань с 2, 4 или 6 очками, а таких граней 3, значит

3 - это число благоприятных исходов

6 - общее число исходов.

Тогда искомая вероятность будет равна

P(А) =3/6;

P(А) =0,5.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

11

Задачи на кубики

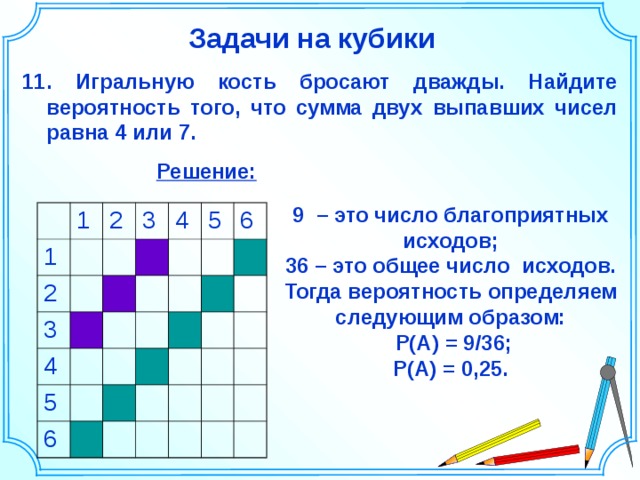
11. Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 4 или 7.

Решение:

9 – это число благоприятных исходов;

36 – это общее число исходов.

Тогда вероятность определяем следующим образом:

P(A) = 9/36;

P(A) = 0,25.

1

1

2

2

3

3

4

4

5

5

6

6

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Задачи на кубики

12. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.

Решение:

115 214 313 412 511

124 223 322 421

133 234 331

142 241

151 Тогда 15 - число благоприятных исходов;

216 – общее число исходов.

Вероятность P(A) = 15/216; P(A) = 0,0694 ≈ 0,07.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

13

Задачи на применение «И-правила», «ИЛИ-правила»

13. Вероятность того, что ручка бракованная, равна 0,05. Покупатель в магазине приобретает случайную упаковку, которая содержит две такие ручки. Найдите вероятность того, что обе ручки в этой упаковке окажутся исправными.

Решение:

Событие А: первая ручка исправна И вторая ручка исправна.

Вероятность, что ручка исправна равна 1- 0,05= 0,95.

Значит вероятность P(A) = 0,95 · 0,95;

P(A) = 0,9025.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

14

Задачи на применение «И-правила», «ИЛИ-правила»

14. Стоянка освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,4. Найдите вероятность того, что за год хотя бы одна лампа не перегорит.

Решение:

Событие А: первая лампа не перегорит И вторая перегорит ИЛИ первая перегорит И вторая лампа не перегорит ИЛИ первая И вторая лампа не перегорят.

Вероятность, что лампа не перегорит равна

p 1 = p 2 = 1 – 0,4 = 0,6.

Тогда P(A) = 0,6 ∙ 0,4 + 0,4 ∙ 0,6 + 0,6 ∙ 0,6 = 0,84.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

15

Задачи на применение «И-правила», «ИЛИ-правила»

15. В первой корзине лежат 2 яблока и 3 груши, а во второй – 3 яблока и 1 груша. Из каждой корзины вынимают наугад по одному фрукту. Какова вероятность того, что это будут два яблока?

Решение:

Событие А: яблоко из первой корзины И

яблоко из второй корзины.

Тогда вероятность достать яблоко из первой корзины p 1 = 2/5 = 0,4; из второй корзины p 2 = 3/4 = 0,75.

А значит вероятность события А равна:

P(A) = 0,4 ∙ 0,75; P(A) = 0,3.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

16

Задачи на применение «И-правила», «ИЛИ-правила»

16. Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).

Решение:

Событие А: попал ИЛИ не попал И попал.

Вероятность того, что стрелок не попадет, равна 1-0,7=0,3

Тогда вероятность события А равна:

P(A) = 0,7 + 0,3 ∙ 0,7 ;

P(A) = 0,91.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

17

Задачи на применение «И-правила», «ИЛИ-правила»

17. В реке водятся пескари и караси. Утром после дождя при однократном закидывании удочки с вероятностью 0,2 попадается пескарь, и с вероятностью 0,1 — карась. Какова вероятность, что один раз забросив удочку, рыбак ничего не поймает?

Решение:

Событие А: поймает карася ИЛИ пескаря.

Значит P(A) = 0,2 + 0,1 = 0,3.

Событие В: ничего не поймает.

Значит, P(В) = 1 - 0,3 = 0,7.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

18

Задачи на применение «И-правила», «ИЛИ-правила»

18. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг. В каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.

Решение:

Событие А: выиграла И ничья ИЛИ ничья И выиграла ИЛИ выиграла И выиграла.

Вероятность ничьи равна: 1 - 0,4 - 0,4 = 0,2.

Тогда P(A) = 0,4 ∙ 0,2 + 0,2 ∙ 0,4 + 0,4 ∙ 0,4 = 0,32.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

19

Задачи на применение «И-правила», «ИЛИ-правила»

19. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет хотя бы один раз.

Решение:

Событие А: орр ИЛИ рор ИЛИ рро ИЛИ оор ИЛИ оро ИЛИ роо ИЛИ оор

Значит вероятность равна:

P(A) = 0,5 ∙ 0,5 ∙ 0,5 + 0,5 ∙ 0,5 ∙ 0,5 + 0,5 ∙ 0,5 ∙ 0,5 + 0,5 ∙ 0,5 ∙ 0,5 + 0,5 ∙ 0,5 ∙ 0,5 + 0,5 ∙ 0,5 ∙ 0,5 + 0,5 ∙ 0,5 ∙ 0,5.

P(A) = 0,875.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

20

Задачи на применение «И-правила», «ИЛИ-правила»

20. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Решение:

Событие А: берет пристрелянный И промахивается ИЛИ берет непристрелянный И промахивается.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

21

Решение:

Вероятность промахнуться из пристрелянного составляет р п = 1-0,9 = 0,1.

Вероятность промахнуться из непристрелянного составляет р н = 1-0,2 = 0,8.

Вероятность взять пристрелянный р пр = 4/10 = 0,4.

Вероятность взять непристрелянный р нп = 6/10 = 0,6.

Значит вероятность события А равна:

P(A) = 0,4 ∙ 0,1+ 0,6 ∙ 0,8;

P(A) = 0,52.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

22

Задачи на применение «И-правила», «ИЛИ-правила»

21. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется  положительным . У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

23

Решение:

Событие А: больной И положительный результат ИЛИ

не больной И положительный результат.

Вероятность того, что пациент болен равна 5% или 0,05.

А вероятность того, что пациент не болен равна 95% или 0,95.

Получаем искомую вероятность:

P(A) = 0,05 ∙ 0,9 + 0,95 ∙ 0,01;

P(A) = 0,0545.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

24

Задачи на применение «И-правила», «ИЛИ-правила»

22. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,3, а при каждом последующем – 0,9. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,96?

Решение:

Вероятность попадания при первом выстреле равна

р 1 = 0,3; вероятность промаха q 1 = 1-0,3 = 0,7.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

25

Решение:

Вероятность попадания при следующих выстрелах равна р 2 = 0,9; вероятность промаха q 2 = 1-0,9 = 0,1.

Пусть система сделала 1 выстрел.

Тогда событие А: система попала, а значит Р(А) = 0,3.

Пусть система сделала 2 выстрела.

Тогда событие А: попала ИЛИ не попала И попала, а

значит Р(А) = 0,3 + 0,7 ∙ 0,9 = 0,93.

Пусть система сделала 3 выстрела.

Тогда событие А: попала ИЛИ не попала И попала ИЛИ не попала И не попала И попала, а

значит Р(А) = 0,3 + 0,7∙ 0,9 + 0,7 ∙ 0,1 ∙ 0,9 = 0,993. Таким образом, нужно сделать 3 выстрела.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

26

Задачи на применение «И-правила», «ИЛИ-правила»

23. Из города в село ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 15 пассажиров, равна 0,64. Вероятность того, что в автобусе окажется меньше 10 пассажиров, равна 0,46. Найдите вероятность того, что в этот день пассажиров будет от 10 до 14.

Решение:

0,64

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

10

15

0,46

х

Значит, искомая вероятность равна 0,46 + х = 0,64;

х = 0,64 – 0,46 = 0,18.

27

Задачи на применение «И-правила», «ИЛИ-правила»

24. Вероятность того, что, выполняя контрольную работу, учащийся М. верно решит больше 4 заданий, равна 0,52. Вероятность того, что М. верно решит больше 3 заданий, равна 0,61. Найдите вероятность того, что М. верно решит ровно 4 задания.

Решение:

0,61

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

3 и более

0,52

х

4 и более

Значит, искомая вероятность равна х + 0,52 = 0,61;

х = 0,61– 0,52 = 0,09.

28

Задачи на применение «И-правила», «ИЛИ-правила»

25. В секции 16 спортсменок, среди них две подруги — Оля и Маша. Спортсменок случайным образом распределяют по 4 равным группам. Найдите вероятность того, что Оля и Маша попадут в одну группу.

Решение:

Событие А: Оля и Маша попадут в первую группу ИЛИ во вторую группу ИЛИ третью группу ИЛИ четвертую группу.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

29

Вероятность того, что Оля попадет в первую группу равна р 1 = 1/4 = 0,25, значит вероятность попадания Маши в эту же группу равна р 2 = 3/15 = 0,2.

Тогда вероятность попадания двух девочек в одну группу равна р = 0,25 ∙ 0,2 = 0,05.

Аналогичная вероятность будет при попадании во 2, 3 и 4 группу, значит, вероятность того, что девочки попадут в одну группу равна

Р(А) = 0,05 + 0,05 + 0,05 +0,05 = 0,2.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

30

Задачи на полную группу событий

26. Два стрелка одновременно стреляют по мишени. Вероятность поражения цели первым стрелком равна 0,6; вторым стрелком равна 0,8. Определить вероятность: а) поражения цели первым стрелком;

б) поражения цели вторым стрелком; в) поражения цели двумя стрелками; г) промаха двумя стрелками.

Решение:

р 1 = 0,6 – вероятность поражения цели 1 стрелком;

q 1 = 1 – 0,6 = 0,4 – вероятность промаха 1 стрелком;

р 2 = 0,8 – вероятность поражения цели 2 стрелком;

q 2 = 1 – 0,8 = 0,2 – вероятность промаха 2 стрелком.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

31

а) Событие А: первый попал И второй промахнулся, значит Р(А) = 0,6 ∙ 0,2 = 0,12.

б) Событие А: первый промахнулся И второй попал, значит Р(А) = 0,4 ∙ 0,8 = 0,32.

в) Событие А: первый попал И второй попал, значит Р(А) = 0,6 ∙ 0,8 = 0,48.

г) Событие А: первый промахнулся И второй промахнулся, значит Р(А) = 0,4 ∙ 0,2 = 0,08.

Все эти события образуют полную группу событий, поэтому их сумма вероятностей равна 1, т.е.

0,12 + 0,32 + 0, 38 + 0,08 = 1.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

32

Задачи на полную группу событий

27. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение:

Событие А: кофе закончится в обоих автоматах означает, что кофе закончится И в одном и в другом, значит вероятность, что кофе закончится в другом автомате равна 0,12 / 0,3 = 0,4.

Следовательно, вероятность того, что кофе останется в одном автомате равна 1- 0,4 = 0,6.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

33

Все эти события образуют полную группу, а именно:

кофе останется в одном автомате И закончится в

другом ИЛИ кофе закончится в одном автомате И

останется в другом ИЛИ кофе останется в двух

автоматах ИЛИ кофе закончится в двух автоматах.

Получаем: 0,6 · 0,3 + 0,6 · 0,3 + х + 0,12 = 1;

х = 1 – 0,48 = 0,52.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

34

Разные задачи на нахождение вероятности

28. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Решение:

Предположим, что 2 фабрики выпускает 10 000 стекол.

• 10 000 ∙ 0, 45 = 4 500 (с.) – выпускает 1 фабрика;

2) 10 000 ∙ 0, 55 = 5 500 (с.) – выпускает 2 фабрика;

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

35

3) 4 500 ∙ 0, 03 = 135 (с.) – бракованных стекол от 1 фабрики;

4) 5 500 ∙ 0, 01 = 55 (с.) – бракованных стекол от 2 фабрики;

5) 135 + 55 = 190 (с.) – всего бракованных стекол.

Значит, общее количество стекол 10 000;

бракованных стекол – 190.

Тогда искомая вероятность равна Р = 190/10 000;

Р = 0,019.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

36

Разные задачи на нахождение вероятности

29. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Решение:

Пусть х – количество яиц из 1 хозяйства, а у – из второго. Тогда 0,4х – яйца высшей категории из 1 хозяйства, 0,2у – яйца высшей категории из второго хозяйства.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

37

Тогда 0,35 ∙ (х+у) – общее количество яиц первой категории.

Приравняем полученные выражения:

0,4х + 0,2у = 0,35 ∙ (х+у);

0,05х = 0,15у;

х = 3у.

Получили, что количество яиц из 1 хозяйства в 3 раза больше, чем из второго.

Значит, общее количество яиц равно у+3у = 4у;

яиц из первого хозяйства 3у.

Тогда искомая вероятность равна Р = 3у/4у = 0,75.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

38

Спасибо за внимание!