Презентация по теме Механические колебания

Н. А. Заболоцкий «Утро»

Рождённый пустыней,

Колеблется звук,

Колеблется синий

На нитке паук.

Колеблется воздух,

Прозрачен и чист,

В сияющих звёздах

Колеблется лист.

• Н. А. Заболоцкий «Утро» Рождённый пустыней, Колеблется звук, Колеблется синий На нитке паук. Колеблется воздух, Прозрачен и чист, В сияющих звёздах Колеблется лист.

Среди всевозможных совершающихся вокруг нас механических движений часто встречаются повторяющиеся движения. Любое равномерное вращение является повторяющимся движением: при каждом обороте всякая точка равномерно вращающегося тела проходит те же положения, что и при предыдущем обороте. Если мы посмотрим, как раскачиваются от ветра ветви и стволы деревьев, как качается на волнах корабль, как движется маятник часов, как движутся взад и вперед поршни и шатуны паровой машины, дизеля, как скачет вверх и вниз игла швейной машины, как качаются качели; если наблюдать чередование морских приливов и отливов, перестановку ног и размахивание руками при ходьбе и беге, биения сердца, пульс, то во всех этих движениях мы заметим одну и ту же черту – многократное повторение одного и того же движения.

КОЛЕБАНИЯ. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

ПЛАН УРОКА:

1.Выяснить, что такое колебание?

2.Условия возникновения колебаний.

3. Виды колебаний.

4. Гармонические колебания.

5. Характеристики гармонического

колебания.

6. Резонанс.

7. Решение задач.

ЧТО ТАКОЕ КОЛЕБАНИЕ?

Колебания- это движения, которые точно или приблизительно повторяются с течением времени.

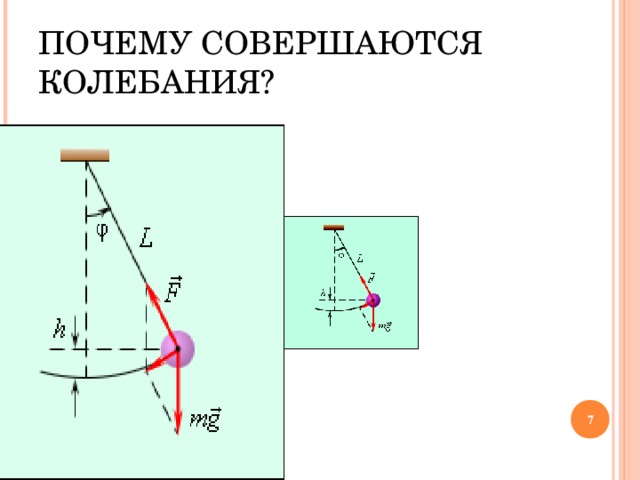
ПОЧЕМУ СОВЕРШАЮТСЯ КОЛЕБАНИЯ?

УСЛОВИЯ ВОЗНИКНОВЕНИЯ КОЛЕБАНИЙ.

1.Вывести тело из

положения равновесия.

2.Уменьшить силу

трения.

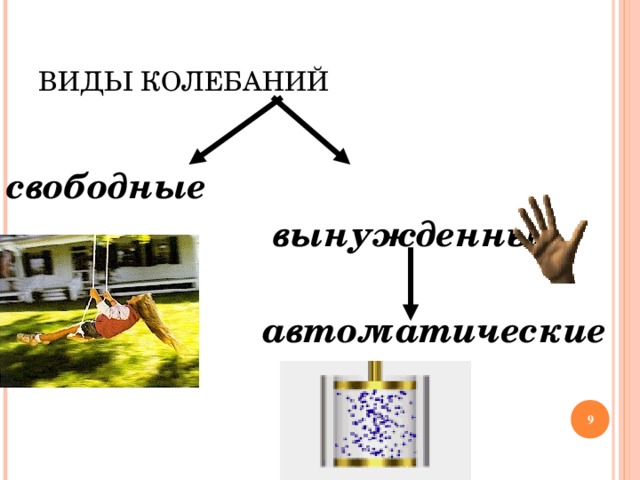
ВИДЫ КОЛЕБАНИЙ

свободные

вынужденные

автоматические

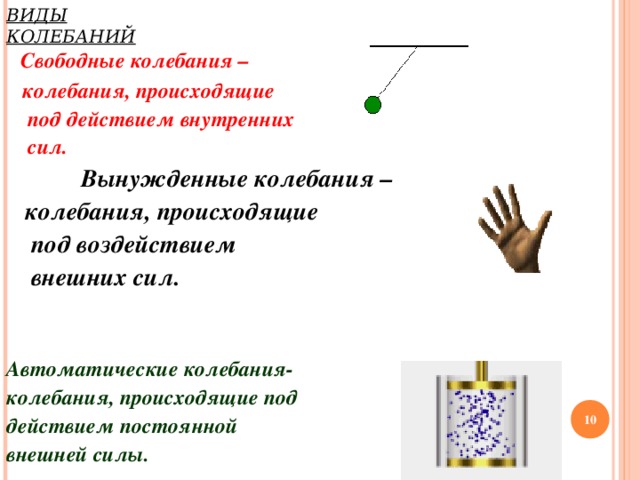
Свободные колебания –

колебания, происходящие

под действием внутренних

сил.

Вынужденные колебания –

колебания, происходящие

под воздействием

внешних сил.

Автоматические колебания-

колебания, происходящие под

действием постоянной

внешней силы.

ВИДЫ КОЛЕБАНИЙ

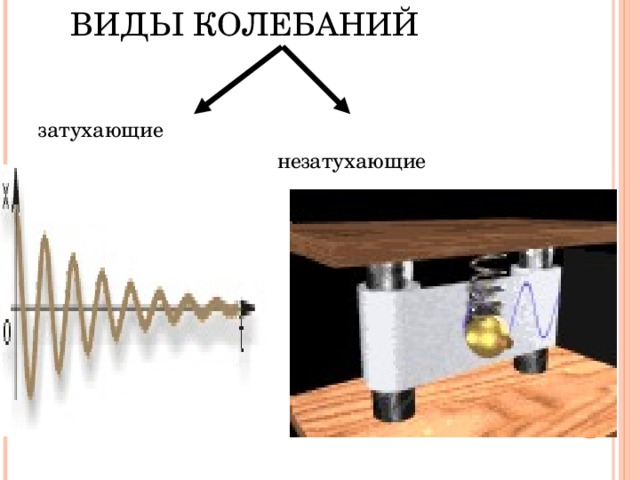
ВИДЫ КОЛЕБАНИЙ

затухающие

незатухающие

Затухающие колебания – это

колебания, которые, под

действием сил

трения или сопротивления,

со временем уменьшаются.

Чтобы затухания не было, на колеблющееся тело должно периодически воздействовать какое-либо внешнее тело. Например, рука человека, подталкивающая качели или волна, поднимающая и опускающая буек, являются такими примерами. Их называют вынужденными.

A 2 A 3 . . . = 0 10 - A 1 5 - A 3 0 t, с 5 - 2 4 6 8 10 12 14 10 - A 2 – – " width="640"

Незатухающие колебания – это колебания, которые со временем не изменяются; силы трения, сопротивления отсутствуют. Для поддержания незатухающих колебаний необходим источник энергии.

X , см

А 1 = А 2 = А 3 = . . . = const

10

A 1 5 A 3

0

t , с

5 2 4 6 8 10 12 14

10

A 2

X, см

А 1 A 2 A 3 . . . = 0

10 -

A 1

5 - A 3

0

t, с

5 - 2 4 6 8 10 12 14

10 - A 2

–

–

1 ВАРИАНТ ВЫПИСЫВАЕТ ПРИМЕРЫ СВОБОДНЫХ КОЛЕБАНИЙ. 2 ВАРИАНТ ВЫПИСЫВАЕТ ПРИМЕРЫ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ.

• колебания листьев на деревьях во время ветра;
• биение сердца;
• колебания качелей;
• колебание груза на пружине;
• перестановка ног при ходьбе;
• колебание струны после того, как её выведут из положения равновесия;
• колебания поршня в цилиндре;
• колебание шарика на нити;
• колебание травы в поле на ветру;
• колебание голосовых связок;
• колебания щёток стеклоочистителя (дворники в машине);
• колебания метлы дворника;
• колебания иглы швейной машины;
• колебания корабля на волнах;
• размахивание руками при ходьбе;
• колебания мембраны телефона;

1 ВАРИАНТ ВЫПИСЫВАЕТ ПРИМЕРЫ ЗАТУХАЮЩИХ КОЛЕБАНИЙ. 2 ВАРИАНТ ВЫПИСЫВАЕТ ПРИМЕРЫ НЕЗАТУХАЮЩИХ КОЛЕБАНИЙ.

• колебания листьев на деревьях во время ветра;
• биение сердца;
• колебания качелей;
• колебание груза на пружине;
• перестановка ног при ходьбе;
• колебание струны после того, как её выведут из положения равновесия;
• колебания поршня в цилиндре;
• колебание шарика на нити;
• колебание травы в поле на ветру;
• колебание голосовых связок;
• колебания щёток стеклоочистителя (дворники в машине);
• колебания метлы дворника;
• колебания иглы швейной машины;
• колебания корабля на волнах;
• размахивание руками при ходьбе;
• колебания мембраны телефона;

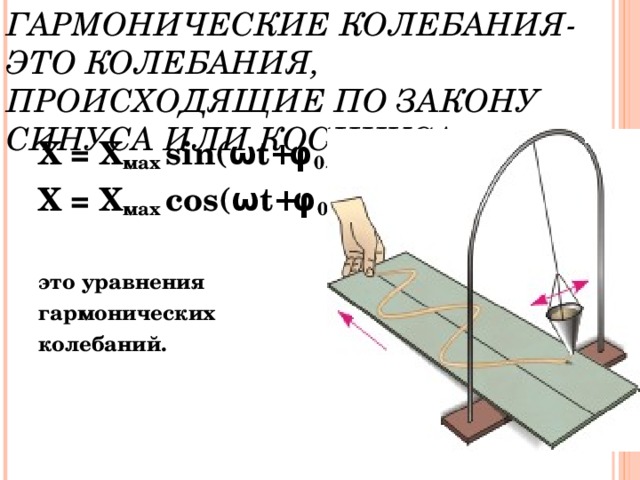
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ- ЭТО КОЛЕБАНИЯ, ПРОИСХОДЯЩИЕ ПО ЗАКОНУ СИНУСА ИЛИ КОСИНУСА.

Х = Х мах sin( ω t + φ 0 )

Х = Х мах cos( ω t + φ 0 )

это уравнения

гармонических

колебаний.

A 2 A 3 . . . = 0 10 - A 1 5 - A 3 0 t, с 5 - 2 4 6 8 10 12 14 10 - A 2 Х- смещение- отклонение тела от положения равновесия [ х ] -м. " width="640"

Х = Х МАХ SIN( Ω T + Φ 0 ) Х = Х МАХ COS( Ω T + Φ 0 )

X , см

А 1 = А 2 = А 3 = . . . = const

10

A 1 5 A 3

0

t , с

5 2 4 6 8 10 12 14

10

A 2

X, см

А 1 A 2 A 3 . . . = 0

10 -

A 1

5 - A 3

0

t, с

5 - 2 4 6 8 10 12 14

10 - A 2

Х- смещение-

отклонение тела от положения равновесия

[ х ] -м.

A 2 A 3 . . . = 0 10 - A 1 5 - A 3 0 t, с 5 - 2 4 6 8 10 12 14 10 - A 2 X , см X , см А 1 = А 2 = А 3 = . . . = const А 1 = А 2 = А 3 = . . . = const 10 10 A 1 5 A 3 A 1 5 A 3 0 0 t , с t , с 5 2 4 6 8 10 12 14 5 2 4 6 8 10 12 14 10 10 A 2 A 2 X, см X, см А 1 A 2 A 3 . . . = 0 А 1 A 2 A 3 . . . = 0 10 - 10 - A 1 A 1 5 - A 3 5 - A 3 0 0 t, с t, с 5 - 2 4 6 8 10 12 14 5 - 2 4 6 8 10 12 14 10 - A 2 10 - A 2 – – – – " width="640"

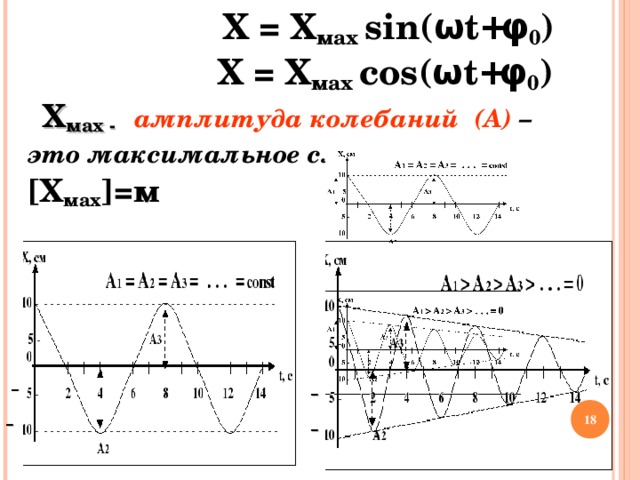
Х = Х мах sin( ω t + φ 0 )

Х = Х мах cos( ω t + φ 0 )

Х мах - амплитуда колебаний (А) –

это максимальное смещение

[ Х мах ] =м

X , см

А 1 = А 2 = А 3 = . . . = const

10

A 1 5 A 3

0

t , с

5 2 4 6 8 10 12 14

10

A 2

X, см

А 1 A 2 A 3 . . . = 0

10 -

A 1

5 - A 3

0

t, с

5 - 2 4 6 8 10 12 14

10 - A 2

X , см

X , см

А 1 = А 2 = А 3 = . . . = const

А 1 = А 2 = А 3 = . . . = const

10

10

A 1 5 A 3

A 1 5 A 3

0

0

t , с

t , с

5 2 4 6 8 10 12 14

5 2 4 6 8 10 12 14

10

10

A 2

A 2

X, см

X, см

А 1 A 2 A 3 . . . = 0

А 1 A 2 A 3 . . . = 0

10 -

10 -

A 1

A 1

5 - A 3

5 - A 3

0

0

t, с

t, с

5 - 2 4 6 8 10 12 14

5 - 2 4 6 8 10 12 14

10 - A 2

10 - A 2

–

–

–

–

Х = Х МАХ SIN( Ω T + Φ 0 ) Х = Х МАХ COS( Ω T + Φ 0 )

Период Т —

время, за которое совершается одно полное колебание.

[ Т ] = с

t время

T = n = число колебаний

=

.

Т

.

X , см

Т

15 v = 0,125 Гц

T

10

5 A

0

t , с

5 2 4 6 8 10 12 14

10

T

15 -

.

.

.

.

.

—

.

.

—

Частота  -

число полных колебаний за единицу времени.

T = v

1 v = T

v = T

1

T = v

T = v

1 v = T

[  ] = Гц (герц)

v = T

1

T = v

Х = Х мах sin( ω t + φ 0 ) Х = Х мах cos( ω t + φ 0 )

Циклической (круговой) частотой  (омега) колебаний

называется число полных колебаний, которые совершаются за 2  единиц времени.

[  ] = рад/с



ω =2 πν

Х = Х мах sin( ω t + φ 0 ) Х = Х мах cos( ω t + φ 0 )

Фаза колебания – ( ω t +  0 ) –

это величина, стоящая под знаком синуса или косинуса. Измеряется в радианах (рад).

Фаза колебания в начальный момент времени ( t =0) называется начальной фазой -  0 . Измеряется в радианах (рад).

ХАРАКТЕРИСТИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

1- название величины

2- определение величины

3- единица измерения

4- формула, по которой

считается величина

МАТЕМАТИЧЕСКИЙ МАЯТНИК

Т- период колебаний

- длина нити

=9,8 –ускорение свободного падения

ПРУЖИННЫЙ МАЯТНИК

m – масса груза

K - жесткость пружины

[K ] =Н/м

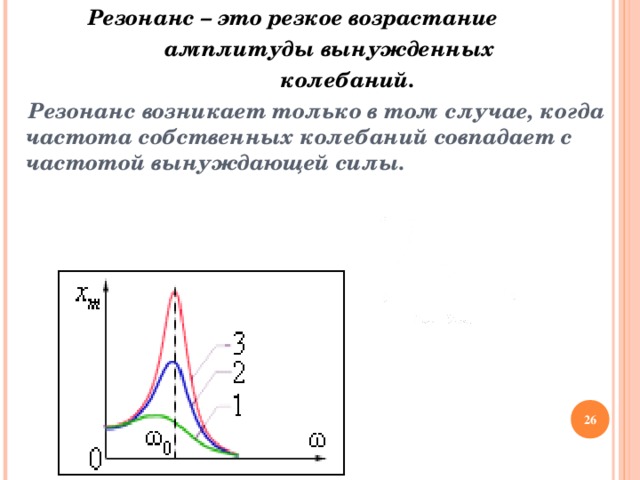
Резонанс – это резкое возрастание

амплитуды вынужденных

колебаний.

Резонанс возникает только в том случае, когда частота собственных колебаний совпадает с частотой вынуждающей силы.

A

0 v

v соб . = v вын .

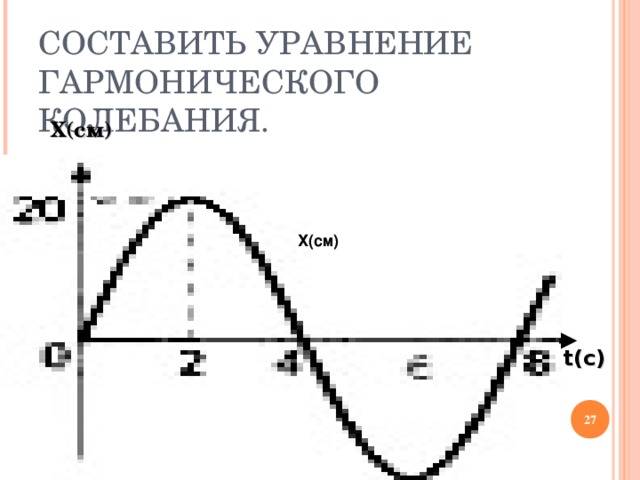
СОСТАВИТЬ УРАВНЕНИЕ ГАРМОНИЧЕСКОГО КОЛЕБАНИЯ.

Х(см)

Х(см)

t (с)

–

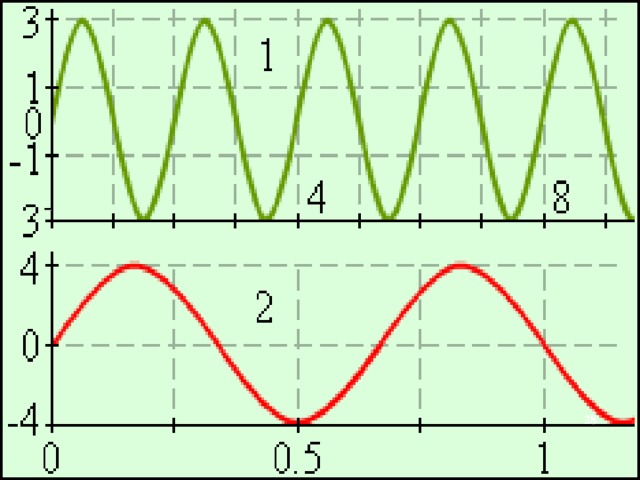
НАЙТИ ВСЁ, ЧТО МОЖНО?

Х = ― 6 cos (100 π t ― π )