
Путешествие в страну
«Рациональных чисел»

Учебник:
Математика: 6 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2018 год
Цель: обобщить полученные знания по умножению, делению, сложению, вычитанию рациональных чисел.
Знать:
правила действий с рациональными числами;
свойства действий с рациональными числами.
Уметь:
применять правила вычисления числовых выражений;
рационально применять свойства действий с рациональными числами;
представлять рациональные числа в виде бесконечной, десятичной, периодической дроби.

Ребята, сегодня мы с вами отправимся в необычное путешествие: мы посетим страну «Рациональных чисел».
В этой стране мы сделаем несколько остановок:
- в деревне Исторической
- на берегу озера Ребусного
- отдохнем на поляне Плоскости
- посетим замок Кроссвордный
- побродим в лесу Сказочном
- попробуем одолеть горы Мозгодром.
На каждой остановке вам надо будет показать свои знания, находчивость и смекалку.
Маршрут путешествия вы будете выбирать сами.
Итак, в путь!
Желаем удачи!

Горы Мозгодром
Карта страны
Лес Сказочный
Поляна Плоскости
Замок Кроссвордный
Деревня Историческая
Озеро Ребусное

Деревня
Историческая

С рациональными числами люди знакомились постепенно. Вначале при счёте предметов возникли натуральные числа. Учёные полагают, что слово для обозначения сотни появилось более 7000 лет назад, для обозначения тысячи – 6000 лет назад, а 5000 лет тому назад в Древнем Египте и в Древнем Вавилоне появляются названия для громадных чисел – до миллиона. Но долгое время натуральный ряд чисел считался конечным: люди думали, что существует самое большое число

- В Европе десятичные дроби ввел в 1585 г. Голландский математик и инженер Симон Стевин.

- Отрицательные числа рассматривал греческий математик Диофант, живший в III веке н.э.
- Ещё раньше с отрицательными числами столкнулись китайские учёные. Это было примерно во II веке н.э.

Отрицательные числа появились позднее, чем дроби. Долгое время такие числа считали «несуществующими», «ложными».
Положительные и отрицательные числа служат для описания изменений величин. Если величина растёт, то говорят, что её изменение положительно, а если она убывает, то изменение называют отрицательным.

Озеро Ребусное
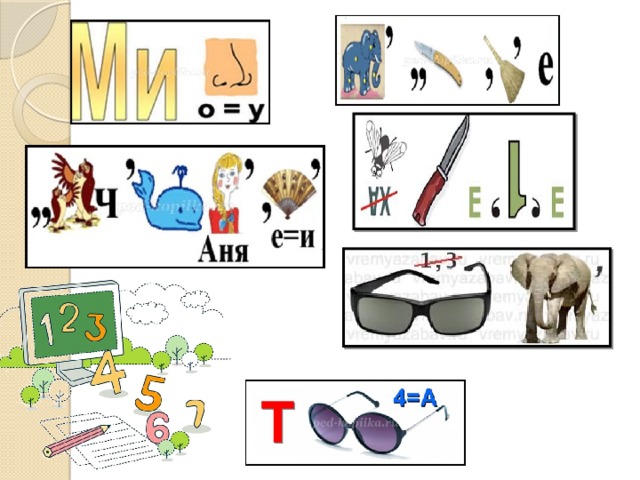

Замок Кроссвордный
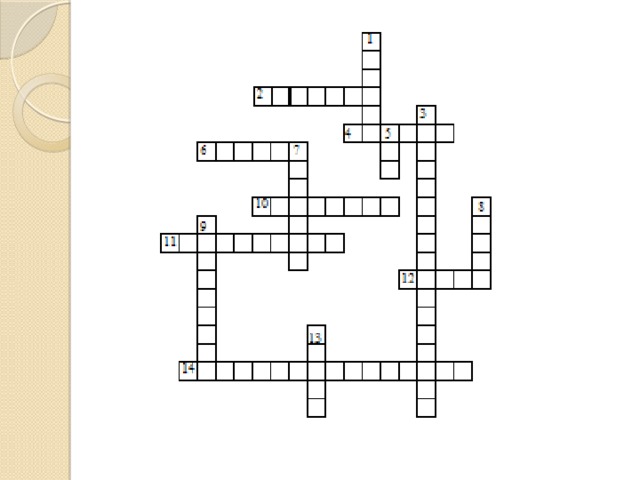

- По горизонтали: 2. Единица с шестью нулями. 4. Единица площади, равная 10000 м 2 . 6. Отрезок, соединяющий центр окружности и любую точку на ней. 10. Суммы длин всех сторон многоугольника. 11. Дробь, у которой числитель меньше знаменателя . 12. Знак, используемый для записи числа. 14. Закон сложения: а + в = в + а.
- По вертикали: 1. Фигуры, совпадающие при наложении . 3. Закон умножения (а + в) с = ас + вс. 5. Прямоугольный параллелепипед, у которого все ребра равны. 7. Название отрезков, из которых состоит треугольник. 8. Единица масс, равная 1000 кг. 9. Равенство, содержащее неизвестное. 14. Третий разряд любого класса.

Горы Мозгодром
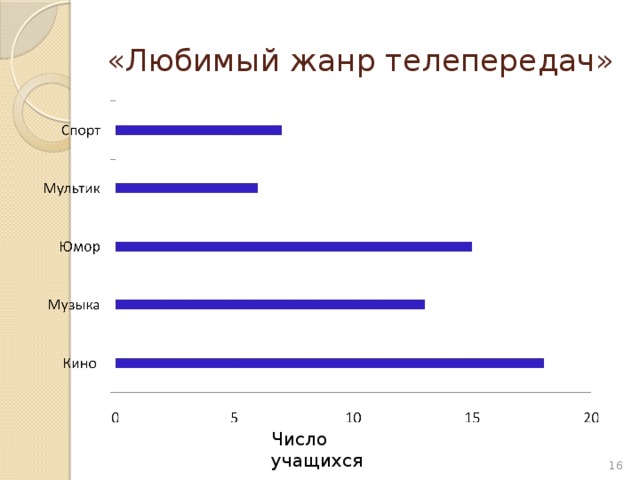
«Любимый жанр телепередач»
Число учащихся
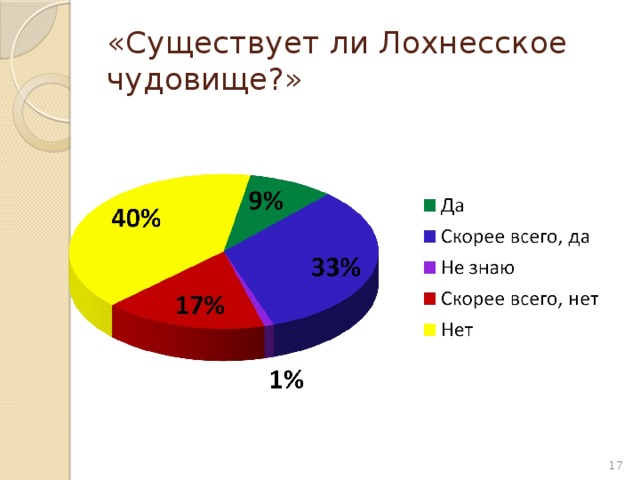
«Существует ли Лохнесское чудовище?»
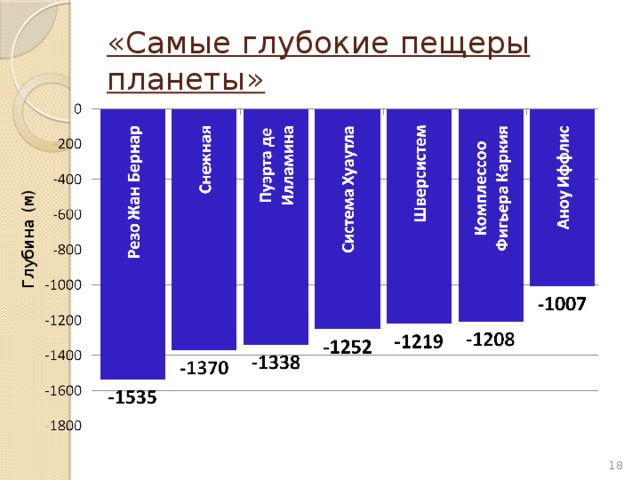
«Самые глубокие пещеры планеты»
Глубина (м)

Поляна Плоскости

- (-9;2)
- (-3;3)
- (0;8)
- (3;3)
- (9;2)
- (5;-3)
- (6;-9)
- (0;-7)
- (-6;-9)
- (-5;-3)
- (-9;2)

Лес Сказочный
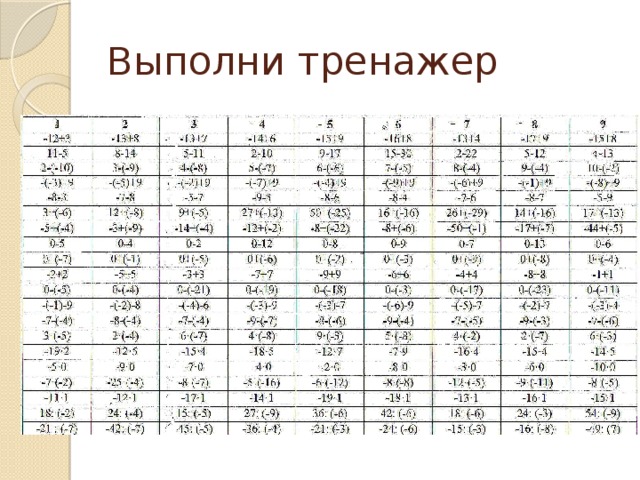
Выполни тренажер

ПОЗДРАВЛЯЕМ!
ВЫ УСПЕШНО ВЫПОЛНИЛИ ВСЕ ЗАДАНИЯ
МОЛОДЦЫ!

 Получите свидетельство
Получите свидетельство Вход
Вход












 Презентация по математике на тему "Рациональные числа и действия на ними" (6класс) (1.69 MB)
Презентация по математике на тему "Рациональные числа и действия на ними" (6класс) (1.69 MB)
 0
0 1647
1647 220
220 Нравится
0
Нравится
0


