Презентация по геометрии "Скалярное произведение векторов"

Скалярное произведение векторов

Подготовила:

Учитель математики первой квалификационной категории

МКОУ Верх-Каргатской СОШ

Балесная Ольга Сергеевна

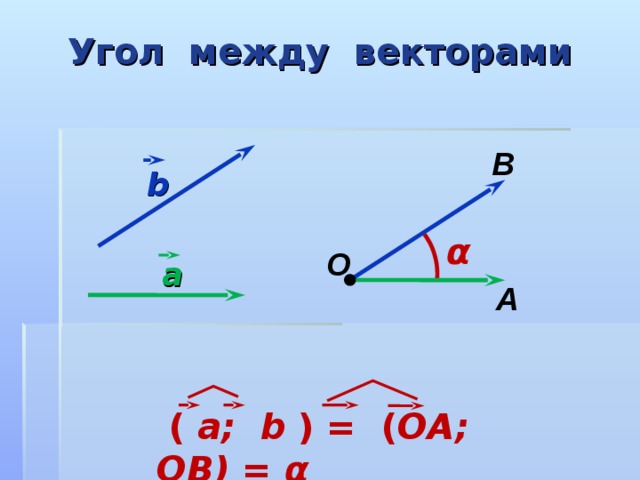
Угол между векторами

В

b

α

О

a

А

( a; b ) = ( ОА; ОВ) = α

Определение скалярного произведения

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

a ∙ b = │a│∙│b│cos ( a; b )

Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны .

a ∙ b = 0  a  b

Скалярное произведение в координатах

Скалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату его длины .

a ∙ a = a 2 = | a | 2

Теорема: скалярное произведение векторов a{x 1 ; y 1 } и b{x 2 ; y 2 } выражается формулой

a ∙ b = x 1 x 2 + y 1 y 2

Скалярное произведение в координатах

Следствие 2: косинус угла между ненулевыми векторами a{x 1 ; y 1 } и b{x 2 ; y 2 } выражается формулой

x 1 x 2 + y 1 y 2

cos α =

√ x 1 2 + y 1 2 ∙ √ x 2 2 + y 2 2

Следствие 1: ненулевые векторы a{x 1 ; y 1 } и b{x 2 ; y 2 } перпендикулярны тогда и только тогда, когда

x 1 x 2 + y 1 y 2 = 0

0 при а ≠ 0. 2 о a ∙ b = b ∙ a (переместительный закон). 3 о ( a + b ) ∙ с = а ∙ с + b ∙ с (распределительный закон). 4 о ( k a ) ∙ b = k ( а ∙ b ) (сочетательный закон). " width="640"

Свойства скалярного произведения

Для любых векторов a , b и c и любого числа k справедливы соотношения:

1 о a 2 ≥ 0 , причем a 2 0 при а ≠ 0.

2 о a ∙ b = b ∙ a (переместительный закон).

3 о ( a + b ) ∙ с = а ∙ с + b ∙ с (распределительный закон).

4 о ( k a ) ∙ b = k ( а ∙ b ) (сочетательный закон).