Презентация "Пирамида". Геометрия 11 класс

Пирамида

Выполнила: Л.В. Делидова

Учитель математики

МАОУ «СОШ №133»

г.Пермь

Пирамида - это многогранник, основание которого многоугольник, а остальные грани - треугольники, имеющие общую вершину

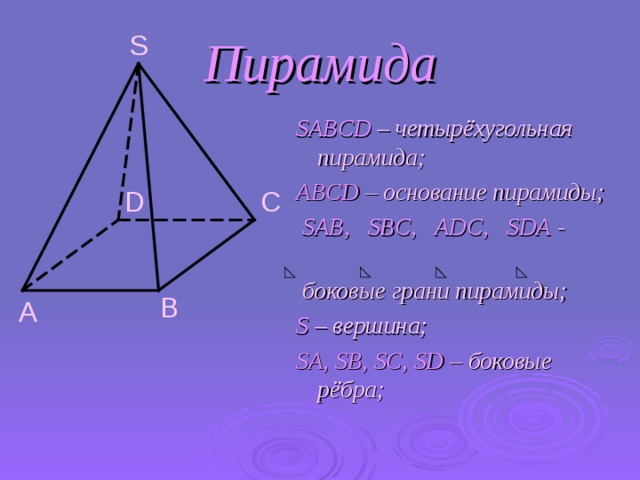
Пирамида

S

SABCD – четырёхугольная пирамида;

ABCD – основание пирамиды;

SAB, SBC, ADC, SDA -

боковые грани пирамиды;

S – вершина;

SA, SB, SC, SD – боковые рёбра;

C

D

B

A

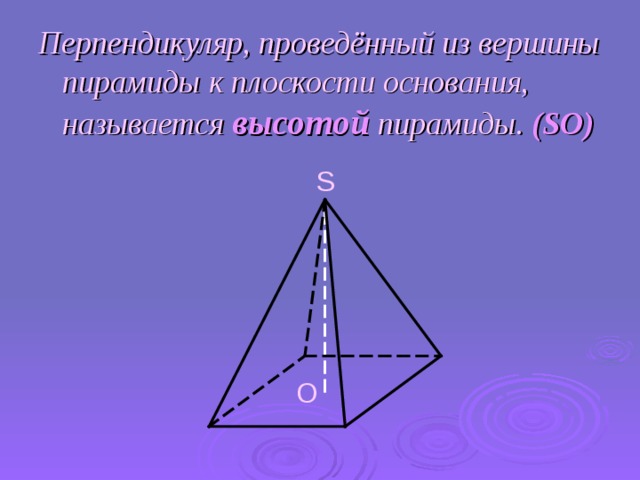
Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды. ( SO)

S

О

Площадью полной поверхности пирамиды называется сумма площадей всех её граней (т.е. основания и боковых граней), а площадью боковой поверхности пирамиды – сумма площадей её боковых граней.

Правильная пирамида

Пирамида называется правильной , если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.

Теорема

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Усечённая пирамида

Если усечённая пирамида получается из правильной пирамиды, то она называется правильной усечённой пирамидой .

Объём V усечённой пирамиды, высота которой равна h , а площади основания равны S и S , вычисляется по формуле

Треугольная пирамида

Треугольная пирамида является четырёхгранником, или тетраэдром

Объём пирамиды

Объём пирамиды равен одной трети произведения площади основания на высоту.

Самая известная на весь мир пирамида – пирамида Хеопса. Её высота составляет около 150 м. (а точнее – 146,6 м.), длина её наклонной стороны – около 235 м., а в основании – квадрат, сторона которого равна 230 м. Вес пирамиды Хеопса около 6,5 млн. тонн.