Презентация на тему "Построение биссектрисы угла"

Построение биссектрисы угла с помощью циркуля и линейки

ПОДГОТОВИЛА учитель математики МБОУ Долботовская СОШ Хатненок А.Ю.

В геометрии важную роль играет треугольник и его элементы. Мы уже умеем строить отрезок, равный данному, угол, равный данному, значит, сможем построить отрезки и углы, равные сторонам и углам данного треугольника. Изучив построение биссектрисы угла, сможем построить биссектрису треугольника.

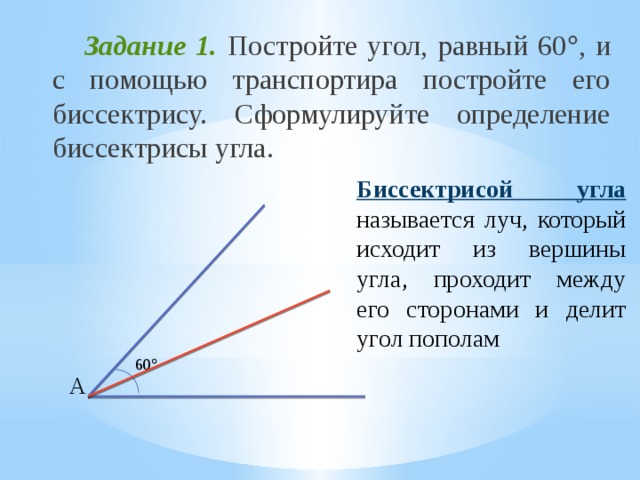
Задание 1. Постройте угол, равный 60  , и с помощью транспортира постройте его биссектрису. Сформулируйте определение биссектрисы угла.

Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам

60 

А

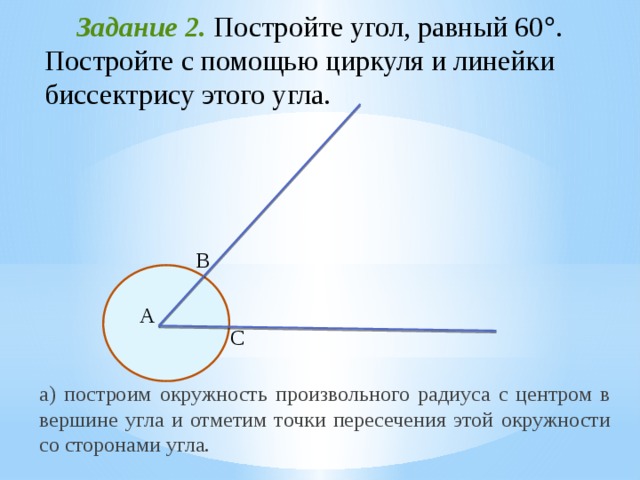
Задание 2. Постройте угол, равный 60  . Постройте с помощью циркуля и линейки биссектрису этого угла.

B

А

C

а) построим окружность произвольного радиуса с центром в вершине угла и отметим точки пересечения этой окружности со сторонами угла.

Задание 2. Постройте угол, равный 60  . Постройте с помощью циркуля и линейки биссектрису этого угла.

B

D

А

C

б) построим две окружности с тем же радиусом, но с центрами в полученных точках на сторонах угла и отметим точку их пересечения.

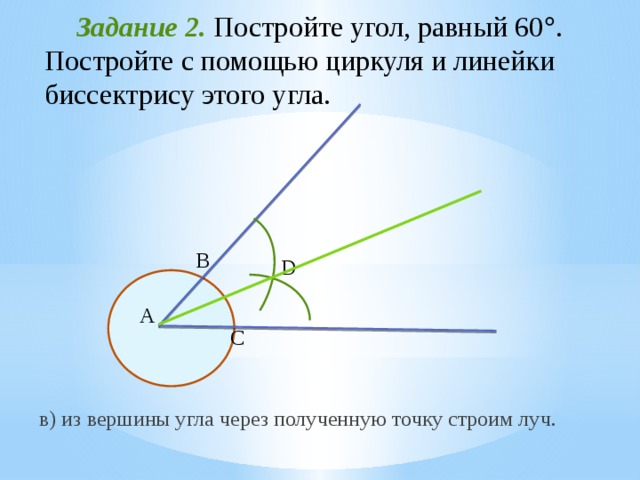
Задание 2. Постройте угол, равный 60  . Постройте с помощью циркуля и линейки биссектрису этого угла.

B

D

А

C

в) из вершины угла через полученную точку строим луч.

Проверим с помощью транспортира, что построенный луч является биссектрисой угла.

 BAD=30 

 CAD=30 

Вывод: мы нашли способ построения биссектрисы угла с помощью циркуля и линейки.

Задание 3. Постройте угол, равный 60  , и с помощью циркуля и линейки постройте биссектрису этого угла, изменив радиусы вспомогательных окружностей.

Проверьте с помощью транспортира , правильно ли построена биссектриса.

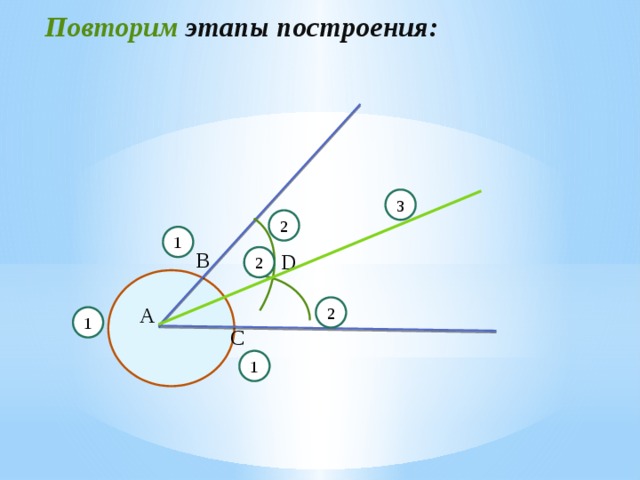
Повторим этапы построения:

3

2

1

B

D

2

2

А

1

C

1

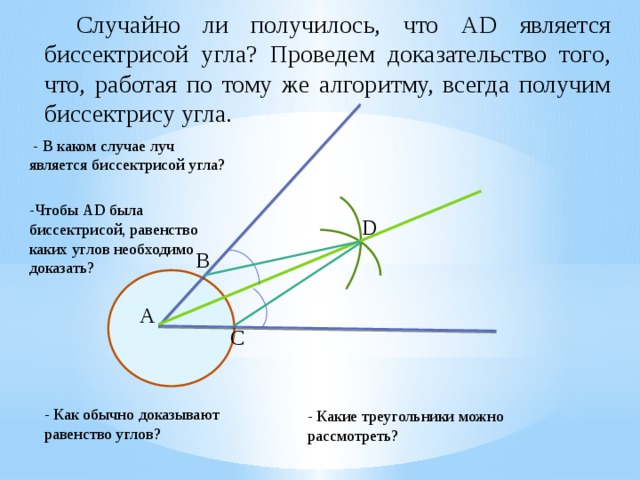
Случайно ли получилось, что АD является биссектрисой угла? Проведем доказательство того, что, работая по тому же алгоритму, всегда получим биссектрису угла.

- В каком случае луч является биссектрисой угла?

-Чтобы АD была биссектрисой, равенство каких углов необходимо доказать?

D

B

А

C

- Как обычно доказывают равенство углов?

- Какие треугольники можно рассмотреть?

Вернемся к каждому шагу построения и посмотрим, какую информацию об этих треугольниках мы можем получить.

- Итак, в нужных треугольниках мы нашли две пары равных элементов. А для равенства треугольников их нужно три. Посмотрим на чертеж, какое условие о нужных нам треугольниках можем выделить?

- Что мы делали на первом шаге и равенство каких элементов треугольников можем отметить?

-Что делали на втором шаге и равенство каких элементов треугольников можно отметить?

D

B

А

C

Доказательство.

Рассмотрим  BAD и  DAC

 BAD=  DAC (по трем сторонам).

Значит,  BAD=  DAC  AD - биссектриса угла A.

Мы построили биссектрису угла с помощью циркуля и линейки и доказали правильность построений. Повторим алгоритм построения биссектрисы угла.

Алгоритм построения биссектрисы угла:

1. построить окружность произвольного радиуса с центром в вершине угла и отметить точки пересечения этой окружности со сторонами угла;

2. построить две окружности с тем же радиусом, но с центрами в полученных точках на сторонах угла и отметить точку их пересечения.

3. из вершины угла через полученную точку построить луч. Этот луч и будет биссектрисой угла.

- Обязательно ли на втором шаге строить окружности тем же радиусом, что и первую?

- Обязательно ли на втором шаге строить окружности одним и тем же радиусом?

- На чем основано доказательство того, что построение выполнено правильно?

- Почему AB=AC?

- Почему BD=CD?

- Какой третий элемент в треугольниках выделяли для равенства треугольников?

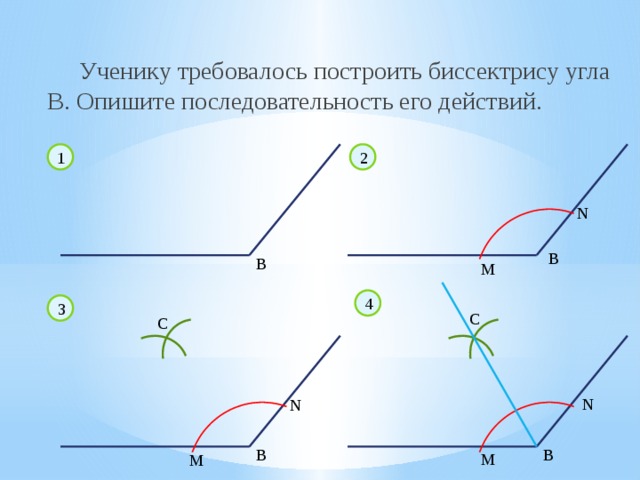
Ученику требовалось построить биссектрису угла B. Опишите последовательность его действий.

1

2

N

B

B

М

4

3

C

C

N

N

B

B

М

М

Задание 5. Постройте угол, равный 81  , и разделите его пополам.

Задание 6.  BAC разделили на четыре равные части. По чертежу объясните процесс деления данного угла на четыре равные части.

Задание 7. Дан  ABC. Постройте биссектрису угла B .

Задание 8. Дан четырехугольник ABCD. Постройте биссектрису угла D.