Презентация на тему "Комбинаторика"

Тема учебного занятия: КОМБИНАТОРИКА

Цели учебного занятия:

• Образовательные:

• познакомить учащихся с новым разделом математики: «Комбинаторика», с его историей, основными понятиями и задачами, использованием в практических целях и в жизни человека; научить в процессе реальной ситуации использовать определения следующих понятий: «перестановки», «размещения», «сочетания»
• познакомить учащихся с новым разделом математики: «Комбинаторика», с его историей, основными понятиями и задачами, использованием в практических целях и в жизни человека;
• научить в процессе реальной ситуации использовать определения следующих понятий: «перестановки», «размещения», «сочетания»
• Развивающие: формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; развивать аналитические способности, логическое мышление; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности .
• формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; развивать аналитические способности, логическое мышление; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности .
• Воспитательные: умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность
• умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность

Задачи учебного занятия:

Познакомить с основными понятиями и формулами комбинаторики и научить решать задачи на заданную тему.

Комбинаторика – это раздел математики, посвященный решению задач  выбора и расположения элементов некоторого множества в соответствии с заданными правилами. Комбинаторика изучает комбинации и перестановки предметов, расположение элементов, обладающее заданными свойствами. Обычные вопросы в комбинаторных задачах: Сколькими способами..? Сколько вариантов..?

N-факториал

N! – это воспроизведение чисел от 1 до n

Например:

5!=1*2*3*4*5=120

Подсчитать: 7! 4! 6!

Основные комбинаторные формулы

• Размещения
• Перестановки
• Сочетания

Размещения

Размещениями  из  n  элементов по  m  элементов называются комбинации, составленные из данных  n элементов по  m  элементов, которые отличаются либо самими элементами, либо порядком элементов.

• Число размещений без повторений  из  n  по  m  ( n  различных элементов) вычисляется по формуле:

• Размещениями с повторениями  из  n  элементов по  m  называются  упорядоченные   m -элементные выборки, в которых элементы могут  повторяться .

Число размещений с повторениями  вычисляется по формуле:

НАПРИМЕР

Возьмем буквы Б, А, Р. Какие размещения из этих букв, взятых по две, можно получить? Сколько таких наборов получиться, если: 1) буквы в Наборе не повторяются; 2) буквы могут повторяться?

Решение.

1) Получатся следующие наборы:  БА, БР, АР, АБ, РБ, РА .

По формуле 1

получаем:  6 наборов

2) Получатся наборы:  ББ, БА, БР, АА, АБ, АР, РР, РБ, РА.

По формуле 2

получаем 9 наборов

Решить: Вдоль дороги стоят 6 светофоров. Сколько может быть различных комбинаций их сигналов, если каждый светофор имеет 3 состояния: "красный", "желтый", "зеленый"?

Перестановки

Перестановками  из  n  элементов называются размещения из этих  n  элементов по  n  (Перестановки - частный случай размещений).

• Число перестановок без повторений  (n различных элементов) вычисляется по формуле:

• Число перестановок c повторениями  ( k  различных элементов, где элементы могут повторяться m1, m2, …, mk раз и m1 + m2 +… + mk = n, где n - общее количество элементов) вычисляется по формуле:

НАПРИМЕР

Возьмем буквы  Б, А, Р . Какие перестановки из этих букв можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) буква А повторяется два раза?

Решение.

1) Получатся наборы: БАР, БРА, АРБ, АБР, РАБ.

По формуле (1) получаем:  P3=1*2*3=6  наборов. 

2) Получатся наборы:  БАРА, БРАА, БААР, ААРБ, ААБР, АБАР, АРАБ, АРБА, АБРА, РАБА, РААБ, РБАА.

По формуле (2) получаем:   наборов

Решить: Сколькими способами можно расставить белые фигуры (2 ладьи, 2 коня, 2 слона, ферзь и король) на первой линии шахматной доски?

Сочетания

Сочетаниями из n элементов по m элементов  называются комбинации, составленные из данных  n  элементов по m  элементов, которые различаются хотя бы одним элементом (отличие сочетаний от размещений в том, что в сочетаниях не учитывается порядок элементов).

• Число сочетаний без повторений  ( n  различных элементов, взятых по  m ) вычисляется по формуле:

• Число сочетаний c повторениями  ( n  элементов, взятых по  m , где элементы в наборе могут повторяться) вычисляется по формуле:

НАПРИМЕР

Возьмем буквы  Б, А, Р . Какие сочетания из этих букв, взятых по две, можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) можно брать по два одинаковые буквы.

Решение.

1) Получатся наборы:  БА  ( БА  и  АБ  - один и тот же набор),  АР  и  РБ .

По формуле (1) получаем:    наборов. 

2) Получатся наборы: ББ, БА, БР, АА, АР, РР.

По формуле (2) получаем:   наборов

Решить: Из 20 учащихся надо выбрать двух дежурных. Сколькими способами это можно сделать?

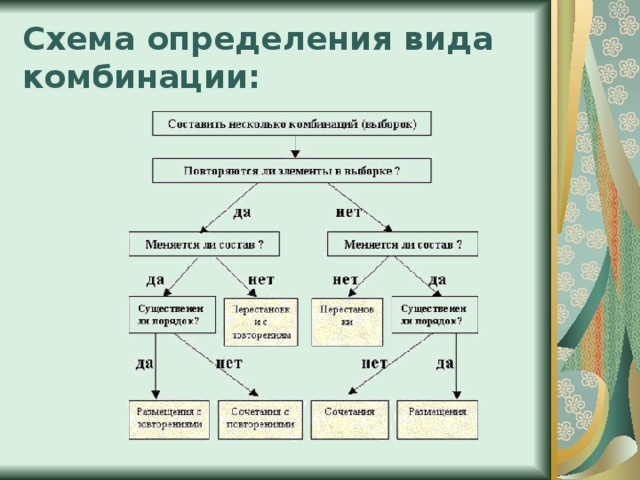
Схема определения вида комбинации:

Решение задач

• У нас есть 9 разных книг из серии “Занимательная математика”. Сколькими способами можно:

1. Расставить их на полке.

2. Подарить три из них победителям школьной олимпиады, занявшим первые три места.

• У бармена есть 6 сортов зеленого чая. Для проведения чайной церемонии требуется подать зеленый чай ровно 3 различных сортов. Сколькими способами бармен может выполнить заказ?
• В группе из 20 студентов надо выбрать 2 представителей для выступления на конференции. Сколькими способами можно это сделать?
• В группе из 20 студентов, среди которых 2 отличника, надо выбрать 4 человека для участия в конференции. Сколькими способами можно выбрать этих четверых, если отличники обязательно должны попасть на конференцию?
• Расписание одного дня содержит 5 уроков. Определить количество таких расписаний при выборе из одиннадцати дисциплин.

Закон умножения

Определение

Закон умножения  в комбинаторике: число сочетаний (способов, комбинаций) в независимых наборах умножается.

Другими словами, пусть имеется  A  способов выполнить одно действием  B  способов выполнить другое действие. Путь также эти действия независимы, т.е. никак не связаны между собой. Тогда можно найти число способов выполнить первое и второе действие по формуле: C  =  A  ·  B .

Закон умножения — это логическое «И», при котором нас интересует одновременное выполнение и первого, и второго действия.

НАПРИМЕР

В корзине лежат 8 белых шаров и 12 черных. Сколькими способами можно достать из этой корзины 2 белых шара и 2 черных?

Решение

Всего в корзине  n  = 8 белых шаров, из которых надо выбрать  k  = 2шара. Это можно сделать  C 8 2  = ... = 28 различными способами.

Кроме того, в корзине имеется  n  = 12 черных шаров, из которых надо выбрать опять же  k  = 2 шара. Число способов сделать это равно C 12 2  = ... = 66.

Поскольку выбор белого шара и выбор черного — события независимые, общее число комбинаций считается по закону умножения:  C  = 28 · 66 = 1848. Как видим, вариантов может быть довольно много.

Закон сложения

• Закон сложения  в комбинаторике: если два взаимоисключающих действия можно выполнить  A  и  B  способами соответственно, то эти события можно объединить. При этом возникнет новое событие, которое можно выполнить  X  =  A  +  B  способами.

Другими словами, при объединении взаимоисключающих действий (событий, вариантов) число их комбинаций складывается.

Можно сказать, что закон сложения — это логическое «ИЛИ» в комбинаторике, когда нас устраивает любой из взаимоисключающих вариантов.

НАПРИМЕР

В корзине лежат 9 черных шаров и 7 красных. Мальчик достает 2 шара одинакового цвета. Сколькими способами он может это сделать?

Решение

Если шары одинакового цвета, то вариантов немного: оба они либо черные, либо красные. Очевидно, что эти варианты — взаимоисключающие.

В первом случае мальчику предстоит выбирать  k  = 2 черных шара из  n  = 9 имеющихся. Число способов сделать это равно  C 9 2  = ... = 36.

Аналогично, во втором случае выбираем  k  = 2 красных шара из  n  = 7 возможных. Число способов равно  C 7 2  = ... = 21.

Осталось найти общее количество способов. Поскольку варианты с черными и красными шарами — взаимоисключающие, по закону сложения имеем:  X  = 36 + 21 = 57.

Решение задач на законы сложения и умножения

• В ларьке продаются 15 роз и 18 тюльпанов. Ученик 9-го класса хочет купить 3 цветка для своей одноклассницы, причем все цветы должны быть одинаковыми. Сколькими способами он может составить такой букет?
• Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать 2-х человек одного пола.
• Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно составить пару из юноши и девушки