Презентация к уроку Термодинамика

Thermodynamics

Born-Haber cycle

Gibbs Free energy

Entropy

Lesson objectives

• Recall the definitions and use of enthalpy and enthalpy change (ΔH) and recognise a range of specific enthalpies

• Calculation of ΔH from bond enthalpies

Success criteria

• Students will be able to:
• Define enthalpy change for different reactions
• Calculate the enthalpy changes using Hess’s law
• Calculate the enthalpy of reaction using bond enthalpies

Revision questions on Hess’s law and bond enthalpies

• 3 Stations work

Formative assessment

• 15 minutes

Lesson objectives

• To construct a Born-Haber cycle
• Calculate the lattice energy using Born-Haber cycle

Success criteria

Students will be able to:

• Construct Born-Haber cycle
• Calculate lattice energy given other energies

Key words

• Enthalpy of atomization

• Electron affinity
• Lattice energy

Definition of key terms

• Ionization energy

• First ionisation energy

The enthalpy change when one mole of gaseous atoms loses one electron per atom to produce gaseous 1+ ions.

It is endothermic (+ve)

Definition of key terms

• Ionization energy

• First ionisation energy

The enthalpy change when one mole of gaseous atoms loses one electron per atom to produce gaseous 1+ ions.

• 2 nd ionisation energy
• The second ionisation energy is when one mole of gaseous 2+ ions is produced from one mole of 1+ ions.
• It is Endothermic (+ve)

• Electron affinity

The enthalpy change when one mole of gaseous atoms gains one electron per atom to produce gaseous 1- ions .

It is exothermic (-ve) for many non-metals

Second electron affinity

The enthalpy change when one mole of gaseous 1- ions gains one electron per ion to produce gaseous 2- ions .

It is endothermic (+ve) as adding –ve electron to –ve ion

• Enthalpy of atomisation

• Enthalpy change when one mole of gaseous atoms is produced from an element in its normal state.
• It is endothermic (+ve)

• Hydration enthalpy

• Enthalpy change when one mole of gaseous ions become hydrated (dissolved in water).
• It is exothermic (-ve)

Bond dissociation enthalpy

Enthalpy change when one mole of covalent bonds is broken in the gaseous state.

e.g.

I-I bond I 2 (g) → 2 I(g)

It is endothermic (+ve)

• Lattice enthalpy

Lattice enthalpy of formation

Enthalpy change when one mole of a solid ionic compound is formed from into its constituent ions in the gas phase

It is exothermic (-ve)

Magnesium chloride

Mg 2+ (g) + 2 Cl - (g) → MgCl 2 (s)

• Lattice enthalpy of dissociation

• Enthalpy change when one mole of a solid ionic compound is broken up into its constituent ions in the gas phase
• It is endothermic (+ve)
• magnesium chloride
• MgCl 2 (s) → Mg 2+ (g) + 2 Cl - (g)

NaC l (s – 411 Enthalpy of sublimation of sodium Na(s) —— Na(g) + 108 Enthalpy of atomisation of chlorine ½C l 2 (g) —— C l (g) + 121 Ist Ionisation Energy of sodium Na(g) —— Na + (g) + e¯ + 500 Electron Affinity of chlorine C l (g) + e¯ —— C l ¯(g) – 364 Lattice Enthalpy of NaC l Na + (g) + C l ¯(g) —— NaC l (s) ? " width="640"

Born-Haber Cycle For Sodium Chloride

kJ mol -1

Enthalpy of formation of NaC l Na(s) + ½C l 2 (g) —— NaC l (s – 411

Enthalpy of sublimation of sodium Na(s) —— Na(g) + 108

Enthalpy of atomisation of chlorine ½C l 2 (g) —— C l (g) + 121

Ist Ionisation Energy of sodium Na(g) —— Na + (g) + e¯ + 500

Electron Affinity of chlorine C l (g) + e¯ —— C l ¯(g) – 364

Lattice Enthalpy of NaC l Na + (g) + C l ¯(g) —— NaC l (s) ?

NaC l (s ) 1 Na(s) + ½C l 2 (g) This is an exothermic process so energy is released. Sodium chloride has a lower enthalpy than the elements which made it. VALUE = - 411 kJ mol -1 1 NaC l (s) " width="640"

Born-Haber Cycle - NaC l

Enthalpy of formation of NaC l

Na(s) + ½C l 2 (g) —— NaC l (s )

1

Na(s) + ½C l 2 (g)

This is an exothermic process so energy is released. Sodium chloride has a lower enthalpy than the elements which made it.

VALUE = - 411 kJ mol -1

1

NaC l (s)

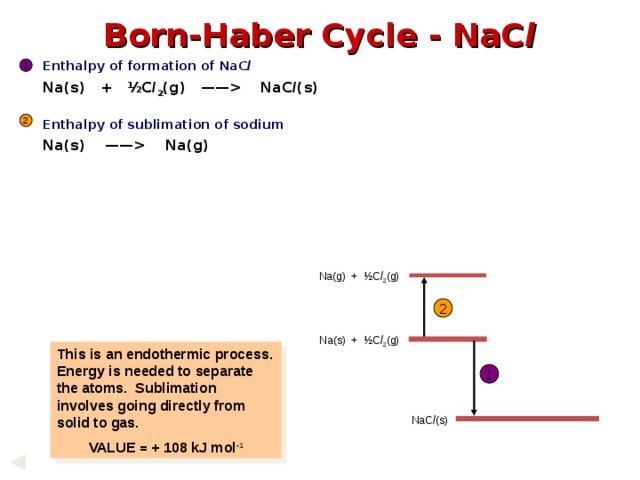NaC l (s) Enthalpy of sublimation of sodium Na(s) —— Na(g) 1 2 Na(g) + ½C l 2 (g) 2 Na(s) + ½C l 2 (g) This is an endothermic process. Energy is needed to separate the atoms. Sublimation involves going directly from solid to gas. VALUE = + 108 kJ mol - 1 1 NaC l (s) " width="640"

Born-Haber Cycle - NaC l

Enthalpy of formation of NaC l

Na(s) + ½C l 2 (g) —— NaC l (s)

Enthalpy of sublimation of sodium

Na(s) —— Na(g)

1

2

Na(g) + ½C l 2 (g)

2

Na(s) + ½C l 2 (g)

This is an endothermic process. Energy is needed to separate the atoms. Sublimation involves going directly from solid to gas.

VALUE = + 108 kJ mol - 1

1

NaC l (s)

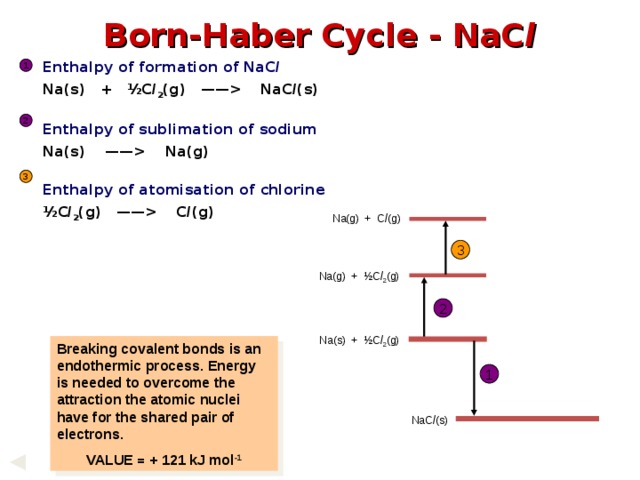NaC l (s) Enthalpy of sublimation of sodium Na(s) —— Na(g) Enthalpy of atomisation of chlorine ½C l 2 (g) —— C l (g) 1 2 3 Na(g) + C l (g) 3 Na(g) + ½C l 2 (g) 2 Na(s) + ½C l 2 (g) Breaking covalent bonds is an endothermic process. Energy is needed to overcome the attraction the atomic nuclei have for the shared pair of electrons. VALUE = + 121 kJ mol -1 1 NaC l (s) " width="640"

Born-Haber Cycle - NaC l

Enthalpy of formation of NaC l

Na(s) + ½C l 2 (g) —— NaC l (s)

Enthalpy of sublimation of sodium

Na(s) —— Na(g)

Enthalpy of atomisation of chlorine

½C l 2 (g) —— C l (g)

1

2

3

Na(g) + C l (g)

3

Na(g) + ½C l 2 (g)

2

Na(s) + ½C l 2 (g)

Breaking covalent bonds is an endothermic process. Energy is needed to overcome the attraction the atomic nuclei have for the shared pair of electrons.

VALUE = + 121 kJ mol -1

1

NaC l (s)

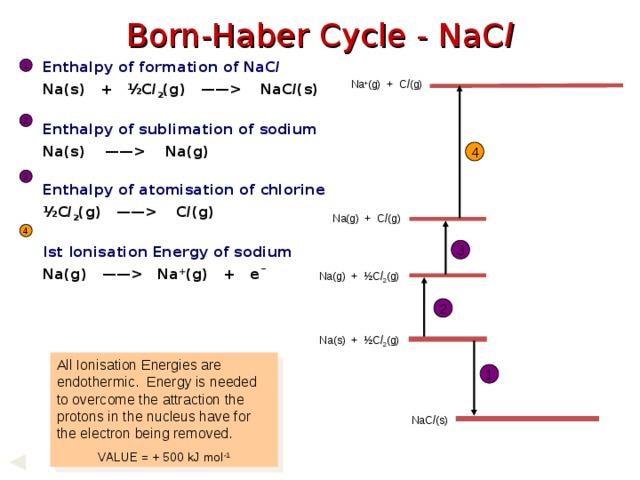NaC l (s) Enthalpy of sublimation of sodium Na(s) —— Na(g) Enthalpy of atomisation of chlorine ½C l 2 (g) —— C l (g) Ist Ionisation Energy of sodium Na(g) —— Na + (g) + e¯ 1 Na + (g) + C l (g) 2 4 3 Na(g) + C l (g) 4 3 Na(g) + ½C l 2 (g) 2 Na(s) + ½C l 2 (g) All Ionisation Energies are endothermic. Energy is needed to overcome the attraction the protons in the nucleus have for the electron being removed. VALUE = + 500 kJ mol -1 1 NaC l (s) " width="640"

Born-Haber Cycle - NaC l

Enthalpy of formation of NaC l

Na(s) + ½C l 2 (g) —— NaC l (s)

Enthalpy of sublimation of sodium

Na(s) —— Na(g)

Enthalpy of atomisation of chlorine

½C l 2 (g) —— C l (g)

Ist Ionisation Energy of sodium

Na(g) —— Na + (g) + e¯

1

Na + (g) + C l (g)

2

4

3

Na(g) + C l (g)

4

3

Na(g) + ½C l 2 (g)

2

Na(s) + ½C l 2 (g)

All Ionisation Energies are endothermic. Energy is needed to overcome the attraction the protons in the nucleus have for the electron being removed.

VALUE = + 500 kJ mol -1

1

NaC l (s)

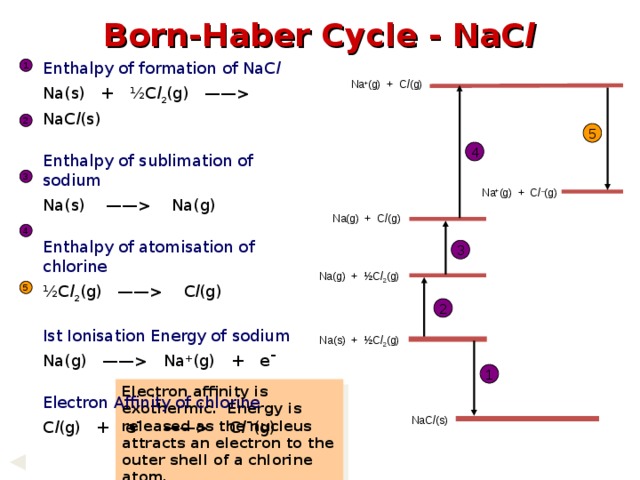NaC l (s) Enthalpy of sublimation of sodium Na(s) —— Na(g) Enthalpy of atomisation of chlorine ½C l 2 (g) —— C l (g) Ist Ionisation Energy of sodium Na(g) —— Na + (g) + e¯ Electron Affinity of chlorine C l (g) + e¯ —— C l ¯(g) 1 Na + (g) + C l (g) 2 5 4 3 Na + (g) + C l – (g) Na(g) + C l (g) 4 3 Na(g) + ½C l 2 (g) 5 2 Na(s) + ½C l 2 (g) 1 Electron affinity is exothermic. Energy is released as the nucleus attracts an electron to the outer shell of a chlorine atom. VALUE = - 364 kJ mol -1 NaC l (s) " width="640"

Born-Haber Cycle - NaC l

Enthalpy of formation of NaC l

Na(s) + ½C l 2 (g) —— NaC l (s)

Enthalpy of sublimation of sodium

Na(s) —— Na(g)

Enthalpy of atomisation of chlorine

½C l 2 (g) —— C l (g)

Ist Ionisation Energy of sodium

Na(g) —— Na + (g) + e¯

Electron Affinity of chlorine

C l (g) + e¯ —— C l ¯(g)

1

Na + (g) + C l (g)

2

5

4

3

Na + (g) + C l – (g)

Na(g) + C l (g)

4

3

Na(g) + ½C l 2 (g)

5

2

Na(s) + ½C l 2 (g)

1

Electron affinity is exothermic. Energy is released as the nucleus attracts an electron to the outer shell of a chlorine atom.

VALUE = - 364 kJ mol -1

NaC l (s)

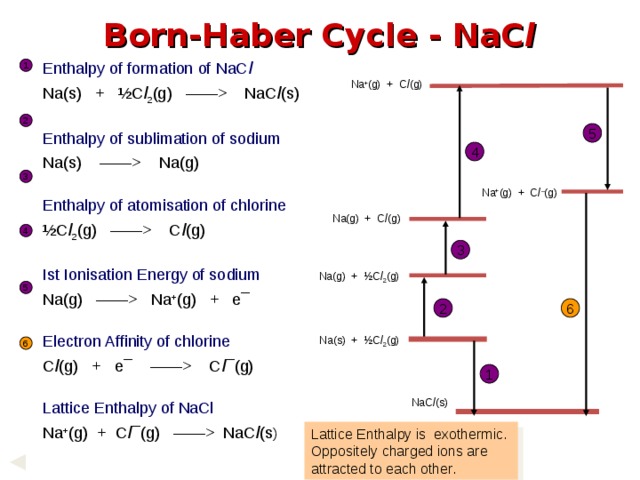NaC l (s) Enthalpy of sublimation of sodium Na(s) —— Na(g) Enthalpy of atomisation of chlorine ½C l 2 (g) —— C l (g) Ist Ionisation Energy of sodium Na(g) —— Na + (g) + e¯ Electron Affinity of chlorine C l (g) + e¯ —— C l ¯(g) Lattice Enthalpy of NaCl Na + (g) + C l ¯(g) —— NaC l (s ) 1 Na + (g) + C l (g) 2 5 4 3 Na + (g) + C l – (g) Na(g) + C l (g) 4 3 Na(g) + ½C l 2 (g) 5 2 6 Na(s) + ½C l 2 (g) 6 1 NaC l (s) Lattice Enthalpy is exothermic. Oppositely charged ions are attracted to each other. " width="640"

Born-Haber Cycle - NaC l

Enthalpy of formation of NaC l

Na(s) + ½C l 2 (g) —— NaC l (s)

Enthalpy of sublimation of sodium

Na(s) —— Na(g)

Enthalpy of atomisation of chlorine

½C l 2 (g) —— C l (g)

Ist Ionisation Energy of sodium

Na(g) —— Na + (g) + e¯

Electron Affinity of chlorine

C l (g) + e¯ —— C l ¯(g)

Lattice Enthalpy of NaCl

Na + (g) + C l ¯(g) —— NaC l (s )

1

Na + (g) + C l (g)

2

5

4

3

Na + (g) + C l – (g)

Na(g) + C l (g)

4

3

Na(g) + ½C l 2 (g)

5

2

6

Na(s) + ½C l 2 (g)

6

1

NaC l (s)

Lattice Enthalpy is exothermic. Oppositely charged ions are attracted to each other.

Born-Haber Cycle - NaC l

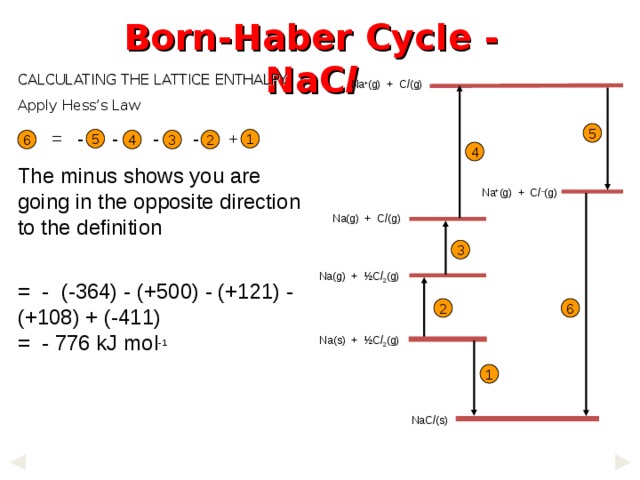
CALCULATING THE LATTICE ENTHALPY

Apply Hess ’s Law

Na + (g) + C l (g)

5

= - - - - +

The minus shows you are going in the opposite direction to the definition

= - (-364) - (+500) - (+121) - (+108) + (-411)

= - 776 kJ mol -1

1

5

2

4

3

6

4

Na + (g) + C l – (g)

Na(g) + C l (g)

3

Na(g) + ½C l 2 (g)

2

6

Na(s) + ½C l 2 (g)

1

NaC l (s)

checkup!!!

Pair (5 minutes)

Construct Born-Haber cycle and calculate the lattice enthalpy of formation of magnesium chloride given the following data:

• ΔH f of magnesium chloride = –642 kJ mol-1
• ΔH a of magnesium = +150 kJ mol-1
• ΔH a of chlorine = +121 kJ mol-1
• 1 st Ionization magnesium = +736 kJ mol-1
• 2nd ionization magnesium = +1450 kJ mol-1
• 1st E.A of chlorine = –364 kJ mol-1

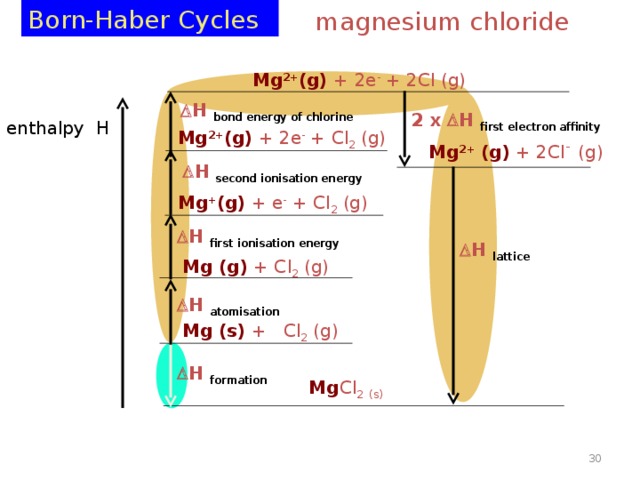
Born-Haber Cycles

magnesium chloride

Mg 2+ (g) + 2e - + 2Cl (g)

 H bond energy of chlorine

2 x  H first electron affinity

enthalpy H

Mg 2+ (g) + 2e - + Cl 2 (g)

Mg 2+ (g) + 2Cl - (g)

 H second ionisation energy

Mg + (g) + e - + Cl 2 (g)

 H first ionisation energy

 H lattice

Mg (g) + Cl 2 (g)

 H atomisation

Mg (s) + Cl 2 (g)

Mg (s) + Cl 2 (g)

 H formation

Mg Cl 2 (s)

Born-Haber Cycles

magnesium chloride

Mg 2+ (g) + 2e - + 2Cl (g)

 H bond energy of chlorine

2 x  H first electron affinity

enthalpy H

Mg 2+ (g) + 2e - + Cl 2 (g)

Mg 2+ (g) + 2Cl - (g)

 H second ionisation energy

Mg + (g) + e - + Cl 2 (g)

 H first ionisation energy

 H lattice

Mg (g) + Cl 2 (g)

 H atomisation

Mg (s) + Cl 2 (g)

 H formation

Mg Cl 2 (s)

29

Apply Hess ’ s Law to calculate ∆H Lattice Energy for MgCl 2 setting out the values in a methodical manner:

1 = 2 + 3 + 4 + 5 + 6 + 7

-641 = +148 + 738 + 1451 + 242 + (2x-364) + ∆H LE

-641 = + 1851 + ∆H LE

∆ H LE = - 1851 - 641 = - 2492 kJ mol -1

30

Lesson objectives

• To compare lattice energy from Born-Haber approach with those from other calculations

Success criteria

Students will be able to:

• Calculate lattice energy using Born Haber cycle
• Compare lattice energy using different approaches
• Account for the differences in different approaches

Keywords

• Ionic charge
• Ionic size
• Polarisation

Activity (15 minutes)

Lattice energy

Experientally (Born-Haber cycle)

Theoriticaly (Coloumbs law)

Coloumb ’s Law

charge A x charge B

distance

Electrostatic energy 

cation charge x anion charge

cation radius + anion radius

  H o lattice

Electrostatic energy 

36

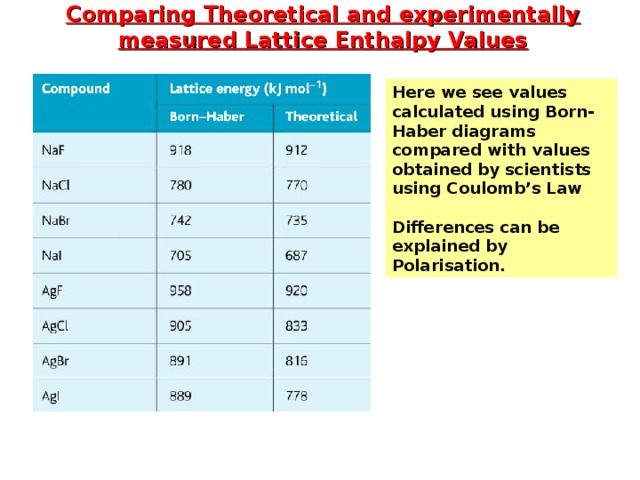
Comparing Theoretical and experimentally measured Lattice Enthalpy Values

Here we see values calculated using Born-Haber diagrams compared with values obtained by scientists using Coulomb’s Law

Differences can be explained by Polarisation.

Polarisation

Ionic bonds can be polarised by the cations strongly attracting the outer shell electrons of the anion.

What does the polarising power of a cation depend on?

• Its charge density , which depends on the size of the ions and its charge.
• Smaller the ionic radius and/or the greater the charge – the greater the charge density.
• For an anion, the larger the radius, the more easily it is polarised.
• The more polarising the positive ion, the more the covalent character.

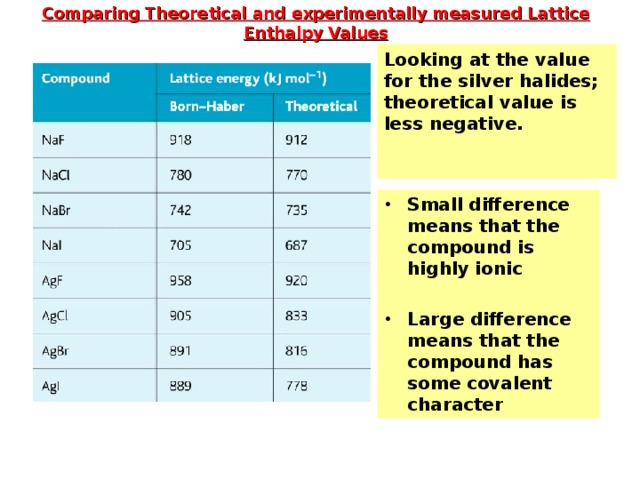
Comparing Theoretical and experimentally measured Lattice Enthalpy Values

Looking at the value for the silver halides; theoretical value is less negative.

• Small difference means that the compound is highly ionic
• Large difference means that the compound has some covalent character

Factors that affect lattice energy

• http://bilimland.kz/en/home#lesson=10363

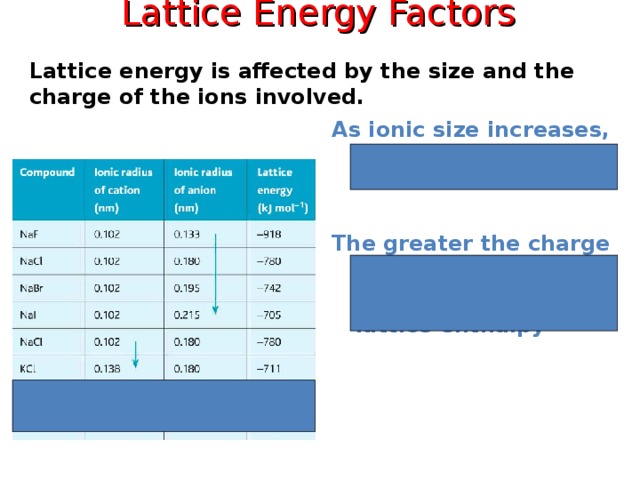
Lattice Energy Factors

Lattice energy is affected by the size and the charge of the ions involved.

As ionic size increases, lattice energy decreases.

The greater the charge on an ion ….

… .. the greater the lattice enthalpy

Lesson objectives

• To understand what are spontaneous reactions.
• To understand that enthalpy change alone is not sufficient to explain spontaneous changes
• To define and use the concept of entropy change (ΔS)

Success criteria

Students will be able to:

• Give factors that determine whether the reaction is spontaneous or not.
• Define entropy
• Calculate entropy change in reactions

Keywords

• Spontaneity
• Entropy
• Degree of disorderly

Spontaneous Processes

• Spontaneous processes occur because they release energy from the system.
• Most spontaneous processes proceed from a system of higher potential energy to a system at lower potential energy.

• Exothermic
• Exothermic

http://bilimland.kz/en/home#lesson=10366 pg 2

Melting Ice

Melting is an endothermic process, yet ice will spontaneously melt above 0 °C.

Ba(OH) 2 8H 2 O( s ) + 2NH 4 NO 3 ( s ) Ba 2+ ( aq ) + 2NO 3 - ( aq ) + 2NH 3 ( aq ) + 10H 2 O( l )

 H o rxn = + 62.3 kJ

The sign of the enthalpy change is insufficient to predict

reaction spontaneity!

.

Factors Affecting Whether Reaction Is Spontaneous

• There are two factors that determine whether a reaction is spontaneous. They are the enthalpy change and the entropy change of the system.
• The enthalpy change, Δ H the size and direction

• The entropy change, Δ S

48

Entropy

• http://bilimland.kz/en/home#lesson=10366
• Pg 3

Entropy

Entropy is a measure of the disorder of a system.

Reactions in which entropy increases as reactants form products tend to be favored. Law of disorder

Factors that affect entropy

Physical states and phase changes

• For a given substance, the entropy of the gas is greater than the entropy of the liquid or the solid. Thus, entropy increases in reactions in which solid reactants form liquid or gaseous products.

Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved.

Dissolution of a solid

• Entropy increases when a substance is divided into parts.

• For instance, entropy increases when an ionic compound dissolves in water.
• For instance, entropy increases when an ionic compound dissolves in water.

Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved.

Number of particles

Entropy tends to increase in chemical reactions in which the total number of product molecules is greater than the total number of reactant molecules.

Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved.

Temperature

• Entropy tends to increase when the temperature increases. As the temperature rises, the molecules move faster and faster, which increases the disorder.

Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved.

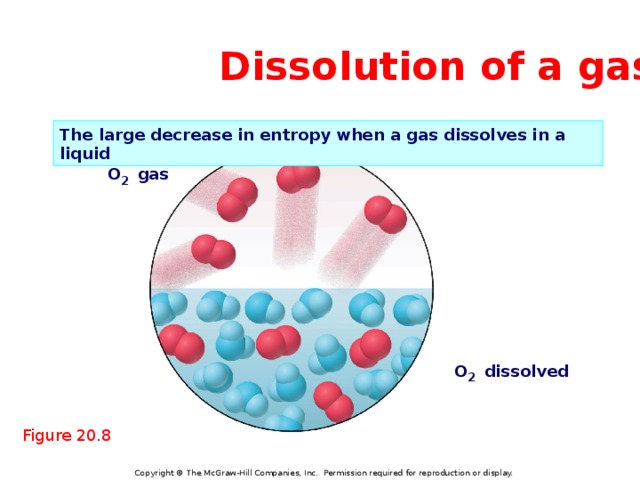
Dissolution of a gas

The large decrease in entropy when a gas dissolves in a liquid

O 2 gas

O 2 dissolved

Figure 20.8

Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display.

Atomic size and molecular complexity

• In similar substances, increases in mass relate directly to entropy e.g CI 4 has higher entropy than CF 4
• In allotropic substances, increases in complexity (e.g., bond flexibility) relate directly to entropy. e.g Carbon(diamond) has less entropy than graphite

The Standard Entropy Change,  S

• The standard entropy change is the difference in absolute entropy between the reactants and products under standard conditions.

 S º reaction = (∑n p S º products ) − (∑n r S º reactants )

• Remember, although the standard enthalpy of formation,  H f °, of an element is 0 kJ/mol, the absolute entropy at 25 °C, S°, is always positive.
• Remember, although the standard enthalpy of formation,  H f °, of an element is 0 kJ/mol, the absolute entropy at 25 °C, S°, is always positive.

Example

PROBLEM:

Calculate  S o rxn for the combustion of 1 mol of propane at 25 o C.

C 3 H 8 ( g ) + 5O 2 ( g ) 3CO 2 ( g ) + 4H 2 O( l )

C3H8(l) = 269.9, O2(g) = 205, CO2(g) = 213.7, H2O(l) = 69.9 J mol-1 K-1

SOLUTION:

 S o rxn = [( 3 mol)(S o CO 2 ) + (4 mol)(S o H 2 O)] - [(1 mol)(S o C 3 H 8 ) + (5 mol)(S o O 2 )]

 S o rxn = [( 3 mol)(213.7 J/mol . K) + (4 mol)(69.9 J/mol . K)] - [(1 mol)(269.9

J/mol . K) + (5 mol)(205.0 J/mol . K)]

 S o rxn = - 374 J/K

Checkup

Calculate the entropy change for this reaction: C2H5OH(l) + 3 O2(g) → 2 CO2(g) + 3 H2O(l)

Entropy: C2H5OH(l) = 161, O2(g) = 205, CO2(g) = 214, H2O(l) = 70 J mol-1 K-1

Activity (10 minutes)

Formative assessment