Презентация к уроку "Решение задач по теме осевая симметрия"

Задача 1.

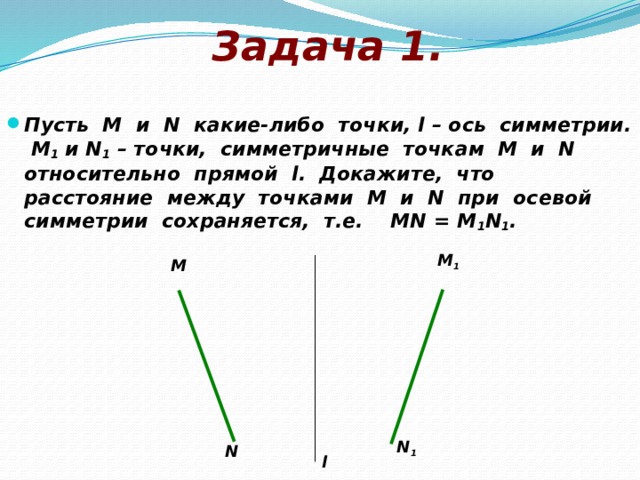
• Пусть М и N какие-либо точки, l – ось симметрии. М 1 и N 1 – точки, симметричные точкам М и N относительно прямой l. Докажите, что расстояние между точками М и N при осевой симметрии сохраняется, т.е. МN = M 1 N 1 .

M 1

M

N 1

N

l

Задача 1. Подсказки:

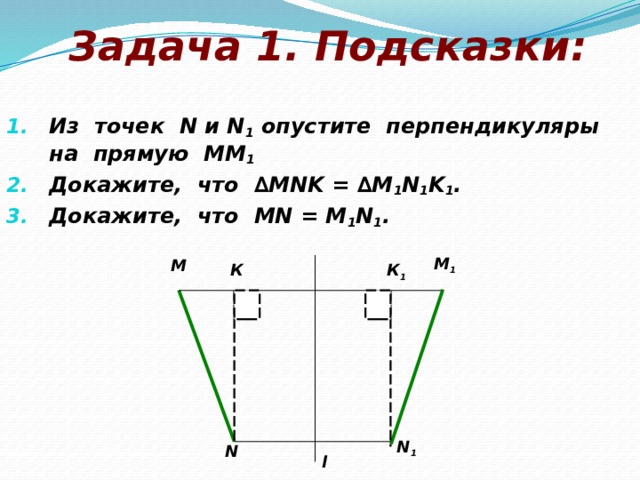
• Из точек N и N 1 опустите перпендикуляры на прямую ММ 1
• Докажите, что ∆MNK = ∆M 1 N 1 K 1 .
• Докажите, что МN = М 1 N 1 .

M 1

M

К

К 1

N 1

N

l

Самостоятельная работа

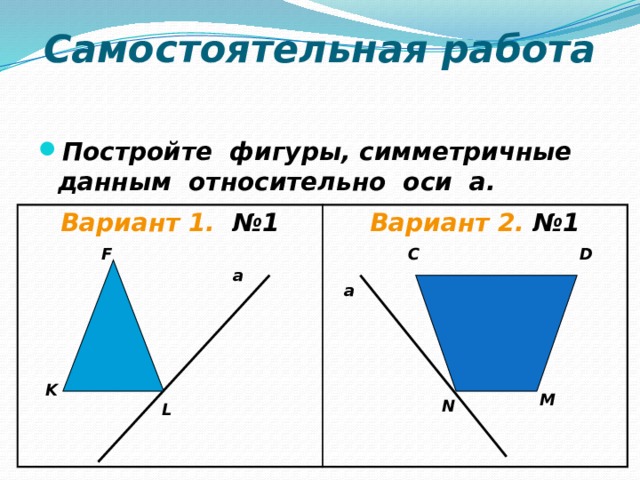
• Постройте фигуры, симметричные данным относительно оси а.

Вариант 1. №1

Вариант 2. №1

C

F

D

а

а

K

M

N

L

Ответьте на вопросы:

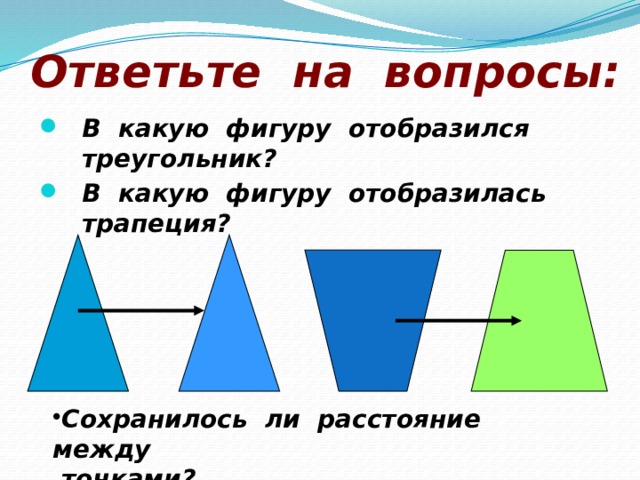
• В какую фигуру отобразился треугольник?
• В какую фигуру отобразилась трапеция?

• Сохранилось ли расстояние между

точками?

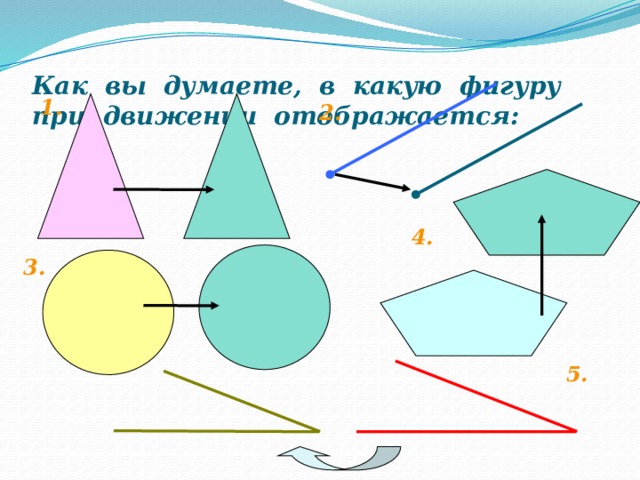
Как вы думаете, в какую фигуру при движении отображается:

1.

2.

4.

3.

5.

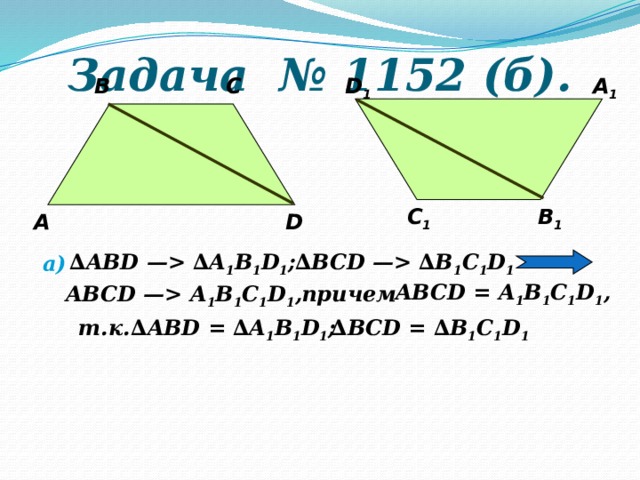
Задача № 1152 (б).

• При движении отрезок отображается на отрезок, треугольник – на равный ему треугольник, угол – на равный ему угол.

• Используя эти свойства движений, можно получить различные способы решений, а именно:

∆B 1 C 1 D 1 ∆ ABD — ∆A 1 B 1 D 1 ; а) ABCD = A 1 B 1 C 1 D 1 , ABCD — A 1 B 1 C 1 D 1 , причем т.к. ∆ ABD = ∆A 1 B 1 D 1 ; ∆ BCD = ∆B 1 C 1 D 1 " width="640"

Задача № 1152 (б).

С

D 1

А 1

В

В 1

С 1

D

А

∆ BCD — ∆B 1 C 1 D 1

∆ ABD — ∆A 1 B 1 D 1 ;

а)

ABCD = A 1 B 1 C 1 D 1 ,

ABCD — A 1 B 1 C 1 D 1 ,

причем

т.к.

∆ ABD = ∆A 1 B 1 D 1 ;

∆ BCD = ∆B 1 C 1 D 1

A 1 D 1 , BC —B 1 C 1 , CD —C 1 D 1 ; AB —A 1 B 1 , б) A — A 1 , B — B 1 , C — C 1 , D — D 1 , BC =B 1 C 1 , CD =C 1 D 1 , AD =A 1 D 1 , AB =A 1 B 1 , причем A = A 1 , B = B 1 , C = C 1 , D = D 1 , тогда ABCD — A 1 B 1 C 1 D 1 , ABCD = A 1 B 1 C 1 D 1 " width="640"

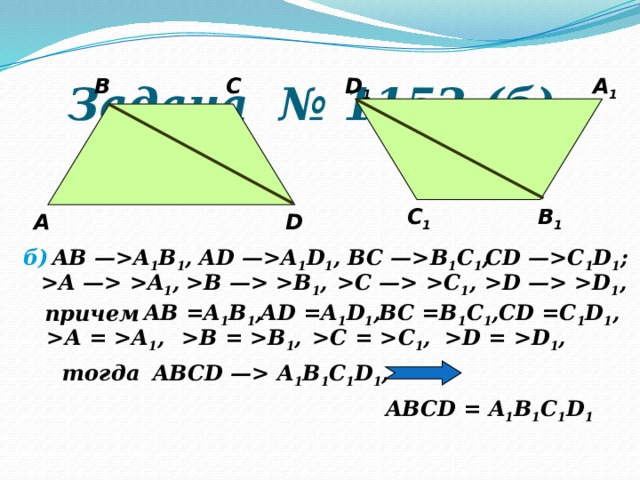
Задача № 1152 (б).

В

С

D 1

А 1

С 1

В 1

А

D

AD —A 1 D 1 ,

BC —B 1 C 1 ,

CD —C 1 D 1 ;

AB —A 1 B 1 ,

б)

A — A 1 ,

B — B 1 ,

C — C 1 ,

D — D 1 ,

BC =B 1 C 1 ,

CD =C 1 D 1 ,

AD =A 1 D 1 ,

AB =A 1 B 1 ,

причем

A = A 1 ,

B = B 1 ,

C = C 1 ,

D = D 1 ,

тогда

ABCD — A 1 B 1 C 1 D 1 ,

ABCD = A 1 B 1 C 1 D 1

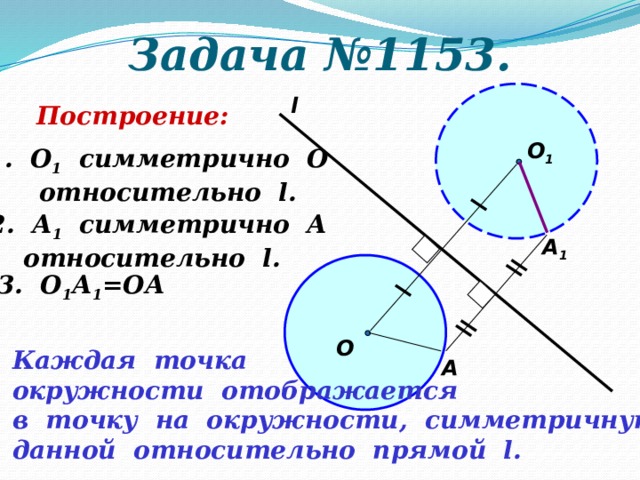
Задача №1153.

l

Построение:

O 1

1. О 1 симметрично О

относительно l.

2. А 1 симметрично А

относительно l.

А 1

3. О 1 А 1 =ОА

О

Каждая точка

окружности отображается

в точку на окружности, симметричную

данной относительно прямой l.

А

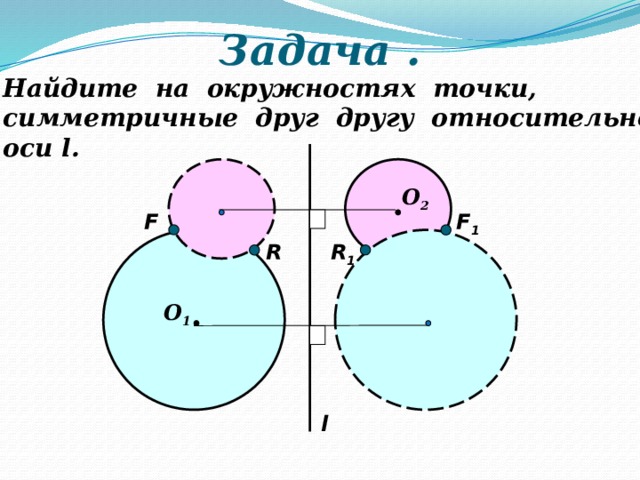
Задача .

Найдите на окружностях точки,

симметричные друг другу относительно

оси l.

О 2

F 1

F

R

R 1

О 1

l

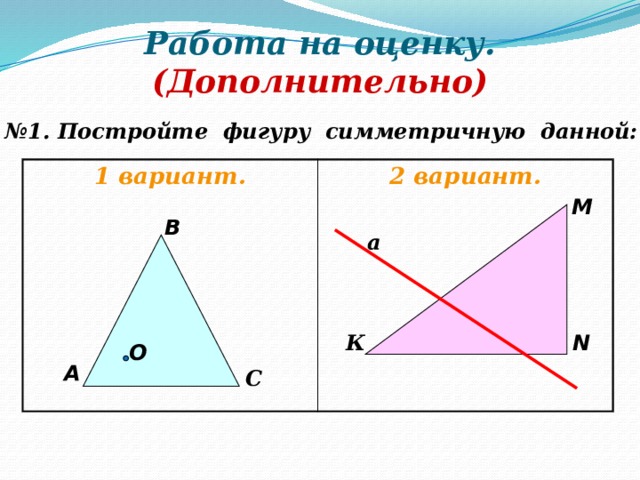
Работа на оценку. (Дополнительно)

№ 1. Постройте фигуру симметричную данной:

1 вариант.

2 вариант.

М

В

a

К

N

O

А

С

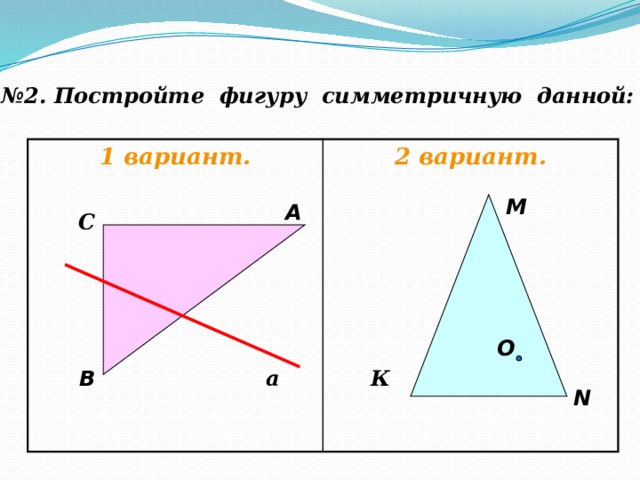
№ 2. Постройте фигуру симметричную данной:

1 вариант.

2 вариант.

М

А

С

О

В

К

a

N