
Основы логики

Термин «логика» происходит от древнегреческого logos – «слово, мысль, понятие, рассуждение, закон».
Логика является одной из дисциплин, образующих математический фундамент информатики.
В вычислительной технике и автоматике используются логические схемы – устройства, которые преобразуют двоичные сигналы.
Анализ и проектирование логических схем опираются на законы алгебры логики.
Любой язык программирования содержит логические переменные и средства для описания и вычисления логических выражений.
Логические методы применяются и при работе с базами данных.

Логика – это наука о законах и формах мышления. Она изучает абстрактное мышление как средство познания объективного мира.

Этапы развития логики
Первые учения о формах и способах рассуждений возникли в странах Дальнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель (384–322 гг. до н.э.), который впервые отделил логические формы речи от ее содержания.

В XVII веке немецкий ученый и философ Готфрид Вильгельм Лейбниц (1646 – 1716) попытался построить первые логические исчисления, усовершенствовал и уточнил логические символы.
На фундаменте, заложенном Лейбницем, другой великий математик, англичанин Джордж Буль (1815-1864) воздвиг здание новой области науки – математической логики.
Начальный раздел математической логики называют алгеброй логики или Булевой алгеброй.

Алгебра логики
С точки зрения устройства ЭВМ нас интересует алгебра логики, в которой не рассматривается конкретное содержание основного понятия логики – высказывания, а важно только истинно оно или ложно.
Основным объектом в логике является высказывание.
Высказывание – это повествовательное предложение,
о котором можно сказать истинно оно или ложно.
Высказывание называется простым ,
если никакая его часть сама
не является высказыванием.
Высказывание называется составным ,
если оно состоит из простых высказываний,
соединенных логическими связками:
И, ИЛИ, частицей НЕ

Примеры:
- Москва – столица России
- Студент математического факультета педагогического университета
- Треугольник АВС подобен треугольнику А ’ В ’ С ’
- Луна есть спутник Марса
- Кислород – газ
- Каша – вкусное блюдо
- Математика – интересный предмет
- Железо тяжелее свинца
- Треугольник называется равносторонним, если все его стороны равны
- Сегодня плохая погода
- Река Ангара впадает в озеро Байкал
Какие из этих предложений являются высказываниями?
Ответ: 1, 4, 5, 8, 9, 11

Основные понятия логики:
Утверждение – высказывание, которое требуется доказать или опровергнуть.
Например: «Сумма внутренних углов треугольника равна 180 0 »
Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом.
Например: «Если хотите начать работать на компьютере, то необходимо сначала включить электропитание»
Умозаключение – логическая операция, в результате которой из одного или нескольких данных высказываний получается (выводится) новое высказывание.
Например: «Все металлы электропроводны». «Ртуть является металлом». Путем умозаключения можно сделать вывод, что «Ртуть электропроводна».
Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты).
Например: (А ۸ (В ۷ С))

Простые высказывания обозначают
заглавными латинскими буквами
A, B, C…X, Y, Z и называют
логическими переменными
Значения высказываний
ИСТИНА или ЛОЖЬ обозначают
соответственно цифрами 1 и 0
и называют логическими величинами
Составные высказывания называются
логическими выражениями и включают
в себя логические переменные,
операции логики и скобки для изменения
порядка действий операций
 3) B = (7 = 3) C = (7 ≠ 3) D = (B ۸ C) = ((7 = 3) ۸ (7 ≠ 3)) На языке алгебры логики эти высказывания можно записать так: A = ИСТИНА = 1 B = ЛОЖЬ = 0 C = ИСТИНА = 1 D = ЛОЖЬ = 0 " width="640"
3) B = (7 = 3) C = (7 ≠ 3) D = (B ۸ C) = ((7 = 3) ۸ (7 ≠ 3)) На языке алгебры логики эти высказывания можно записать так: A = ИСТИНА = 1 B = ЛОЖЬ = 0 C = ИСТИНА = 1 D = ЛОЖЬ = 0 " width="640"
Примеры:
Рассмотрим следующие высказывания:
- A = (7 3)
- B = (7 = 3)
- C = (7 ≠ 3)
- D = (B ۸ C) = ((7 = 3) ۸ (7 ≠ 3))
На языке алгебры логики эти высказывания можно записать так:
A = ИСТИНА = 1
B = ЛОЖЬ = 0
C = ИСТИНА = 1
D = ЛОЖЬ = 0

Основные логические операции
Логическая операция КОНЪЮНКЦИЯ
(логическое умножение)
Ставит в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказываний истинны.
Соответствует союзу И
Обозначается & или ۸
А
0
В
0
А ۸ В
0
1
0
1
1
0
0
0
1
1

Примеры:
Определить значения истинности следующих высказываний:
- Ленинград расположен на Неве и 2 + 3 = 5
- 7 – простое число и 9 – простое число
- 2 * 2 = 4 и 2 * 2 ≤ 5 и 2 * 2 ≥ 4
- Москва – столица России и Екатеринбург – столица Сибири
- Книга – источник информации и 5 не больше 8
- Девочки обычно любят играть в куклы и Не любая машина - автомобиль
- Все гуси – птицы и Все игрушки - машины
Ответ: истинными высказываниями являются: 1, 3, 5, 6
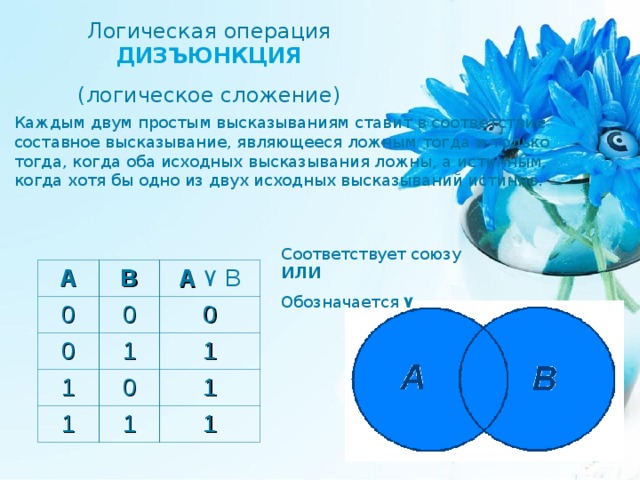
Логическая операция ДИЗЪЮНКЦИЯ
(логическое сложение)
Каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, а истинным, когда хотя бы одно из двух исходных высказываний истинно.
Соответствует союзу ИЛИ
Обозначается ۷
А
0
В
0
0
А ۷ В
1
0
1
1
1
0
1
1
1

Примеры:
Определить значения истинности следующих высказываний:
- 7 – простое число или 9 – простое число
- Число 2 четное или Это простое число
- 2 * 2 = 4 или Белые медведи живут в Африке
- Каша – вкусное блюдо или Математика – интересный предмет
- Луна – спутник Марса или Луна – спутник Земли
- Сегодня плохая погода или Кислород – вода
- Microsoft Word – текстовый редактор или Paint – графический редактор
Ответ: истинными высказываниями являются: 1, 2, 3, 5, 7

Логическая операция ИНВЕРСИЯ
(отрицание)
Каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицает.
Соответствует частице НЕ
Обозначается А
А
0
Ā
1
1
0
 3. 4 ≤ 5. Ответ: истинными высказываниями являются: 2 " width="640"
3. 4 ≤ 5. Ответ: истинными высказываниями являются: 2 " width="640"
Примеры:
Сформулируйте отрицания следующих высказываний и укажите значения истинности полученных отрицаний:
- Волга впадает в Каспийское море.
- Число 28 не делится на число 7.
- 6 3.
- 4 ≤ 5.
Ответ: истинными высказываниями являются: 2
 А 0 В 0 0 А = В 1 1 1 1 1 0 1 0 1 " width="640"
А 0 В 0 0 А = В 1 1 1 1 1 0 1 0 1 " width="640"
Логическая операция ИМПЛИКАЦИЯ
(логическое следование)
Ставит в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
Соответствует обороту ЕСЛИ…, ТО…
Обозначается =
А
0
В
0
0
А = В
1
1
1
1
1
0
1
0
1

Примеры:
Определить значения истинности следующих высказываний:
- Если 12 делится на 6, то 12 делится на 3.
- Если 11 делится на 6, то 11 делится на 3.
- Если 15 делится на 6, то 15 делится на 3.
- Если 15 делится на 3, то 15 делится на 6.
- Если Саратов расположен на Неве, то белые медведи обитают в Африке.
Ответ: истинными высказываниями являются: 1, 2, 3, 5

Логическая операция ЭКВИВАЛЕНЦИЯ
(равнозначность)
Ставит в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Соответствует оборотам:
ТОГДА И ТОЛЬКО ТОГДА;
В ТОМ И ТОЛЬКО В ТОМ СЛУЧАЕ Обозначается ↔ ; ~
А
0
В
0
0
А ↔ В
1
1
1
1
0
0
1
0
1

Примеры:
Определить значения истинности следующих высказываний:
- 12 делится на 6 тогда и только тогда, когда 12 делится на 3.
- 11 делится на 6 тогда и только тогда, когда 11 делится на 3.
- 15 делится на 6 тогда и только тогда, когда 15 делится на 3.
- 15 делится на 5 тогда и только тогда, когда 15 делится на 4.
Ответ: истинными высказываниями являются: 1, 2
 В А ۸ В 1 1 0 0 А ۷ В 0 1 А 1 В 0 1 0 0 0 1 0 0 1 ¯ А 1 0 1 1 1 1 1 0 1 1 0 0 " width="640"
В А ۸ В 1 1 0 0 А ۷ В 0 1 А 1 В 0 1 0 0 0 1 0 0 1 ¯ А 1 0 1 1 1 1 1 0 1 1 0 0 " width="640"
Объединенная таблица истинности
А ۷ В
А ↔ В
А = В
А ۸ В
1
1
0
0
А ۷ В
0
1
А
1
В
0
1
0
0
0
1
0
0
1
¯ А
1
0
1
1
1
1
1
0
1
1
0
0

 Получите свидетельство
Получите свидетельство Вход
Вход











 Презентация к уроку "Основы логики" (405 KB)
Презентация к уроку "Основы логики" (405 KB)
 0
0 2075
2075 193
193 Нравится
0
Нравится
0



