Презентация к ОГЭ

ПРАКТИЧЕСКИЙ СЕМИНАР ПОДГОТОВКИ К ИТОГОВОЙ АТТЕСТАЦИИ ОСНОВНОЙ ШКОЛЫ МОДУЛЬ «ГЕОМЕТРИЯ»

Составила учитель математики

Максимова Т.М.

МОУ Первомайская СОШ

Треугольники

Медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.

Каждая медиана делит треугольник на два равновеликих треугольника.

Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника.

Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.

Если угол одного треугольника равен углу другого треугольника, то площадь этих треугольников относятся как произведения сторон, заключающих равные углы.

Правильный треугольник

Задание 1. Дан правильный треугольник со стороной 6. Найдите:

1) периметр; 2) высоту; 3) площадь; 4) радиус вписанной окружности;

5) длину вписанной окружности; 6) площадь вписанного круга;

7) радиус описанной окружности; 8) длину описанной окружности;

9) площадь описанного круга; 10) площадь четырёхугольника ОА 1 СВ 1 .

Решение.

1) Периметр треугольника равен сумме всех его сторон: Р=6+6+6=18.

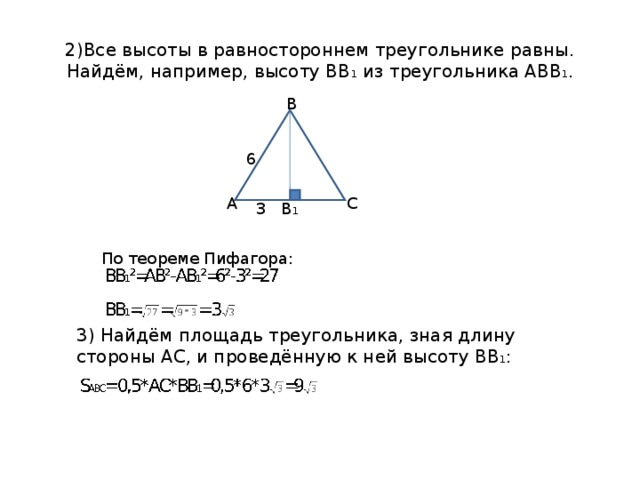
2)Все высоты в равностороннем треугольнике равны. Найдём, например, высоту ВВ 1 из треугольника АВВ 1 .

В

6

А

С

В 1

3

По теореме Пифагора:

3) Найдём площадь треугольника, зная длину стороны АС, и проведённую к ней высоту ВВ 1 :

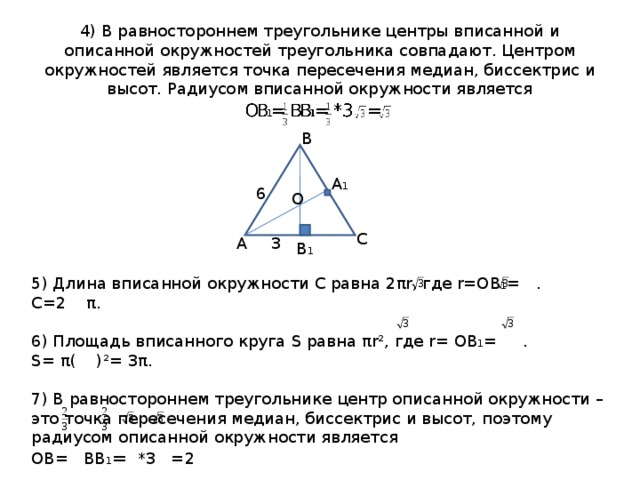
4) В равностороннем треугольнике центры вписанной и описанной окружностей треугольника совпадают. Центром окружностей является точка пересечения медиан, биссектрис и высот. Радиусом вписанной окружности является

В

А 1

6

О

С

3

А

В 1

5) Длина вписанной окружности С равна 2 π r , где r =ОВ 1 = . С=2 π .

6) Площадь вписанного круга S равна π r² , где r = ОВ 1 = . S = π ( )²= 3 π .

7) В равностороннем треугольнике центр описанной окружности – это точка пересечения медиан, биссектрис и высот, поэтому радиусом описанной окружности является

ОВ= ВВ 1 = *3 =2

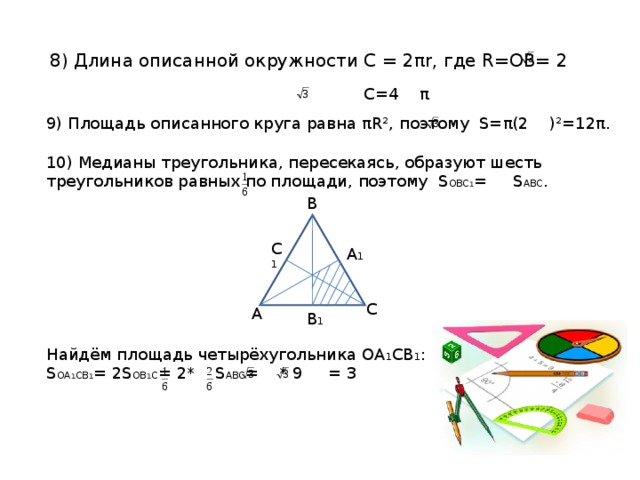
8) Длина описанной окружности С = 2 π r , где R=OB= 2

C=4 π

9) Площадь описанного круга равна π R² , поэтому S= π (2 )²=12 π .

10) Медианы треугольника, пересекаясь, образуют шесть треугольников равных по площади, поэтому S OBC 1 = S ABC .

Найдём площадь четырёхугольника ОА 1 СВ 1 :

S OA 1 CB 1 = 2S OB 1 C = 2* S ABC = * 9 = 3

B

C 1

A 1

C

A

B 1

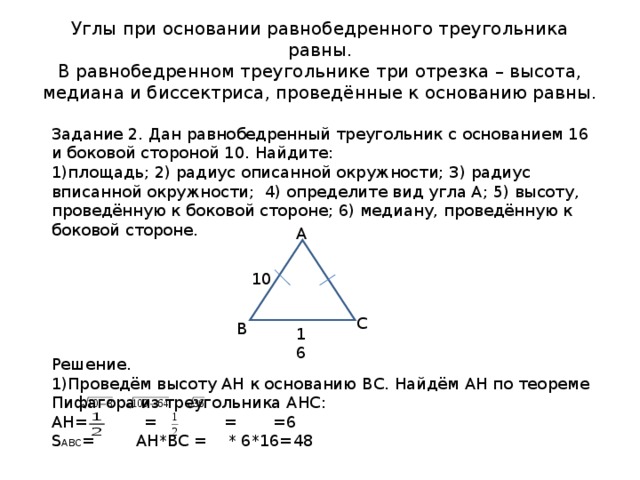
Углы при основании равнобедренного треугольника равны. В равнобедренном треугольнике три отрезка – высота, медиана и биссектриса, проведённые к основанию равны.

Задание 2. Дан равнобедренный треугольник с основанием 16 и боковой стороной 10. Найдите:

• площадь; 2) радиус описанной окружности; 3) радиус вписанной окружности; 4) определите вид угла А; 5) высоту, проведённую к боковой стороне; 6) медиану, проведённую к боковой стороне.

Решение.

• Проведём высоту АН к основанию ВС. Найдём АН по теореме Пифагора из треугольника АНС:

АН= = = =6

S АВС = АН*ВС = * 6*16=48

А

10

С

В

16

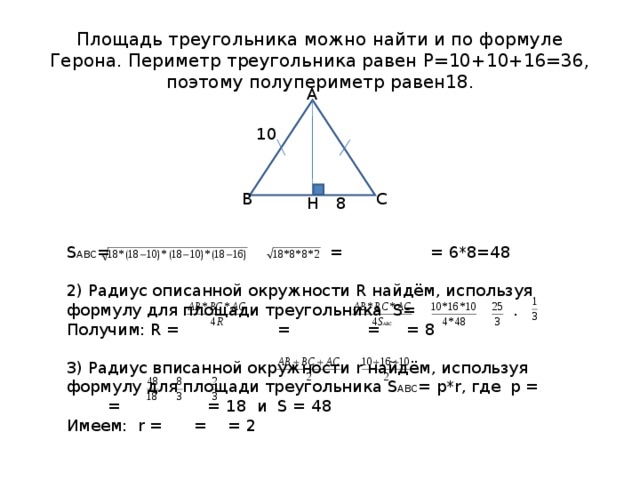
Площадь треугольника можно найти и по формуле Герона. Периметр треугольника равен Р=10+10+16=36, поэтому полупериметр равен18.

А

S АВС = = = 6*8=48

2) Радиус описанной окружности R найдём, используя формулу для площади треугольника S= . Получим: R = = = = 8

3) Радиус вписанной окружности r найдём, используя формулу для площади треугольника S ABC = p*r , где p = = = 18 и S = 48

Имеем: r = = = 2

10

В

С

8

Н

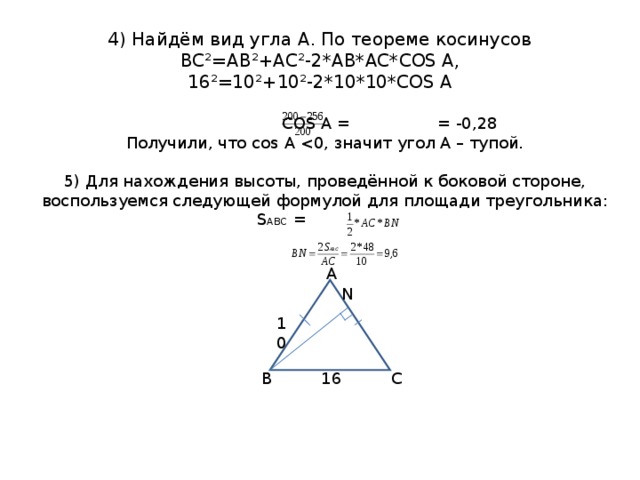
4) Найдём вид угла А. По теореме косинусов ВС²=АВ²+АС²-2*АВ*АС* COS А, 16²=10²+10²-2*10*10*СО S А

С OS A = = -0 ,28

Получили, что со s А

5) Для нахождения высоты, проведённой к боковой стороне, воспользуемся следующей формулой для площади треугольника:

S ABC =

A

N

10

B

C

16

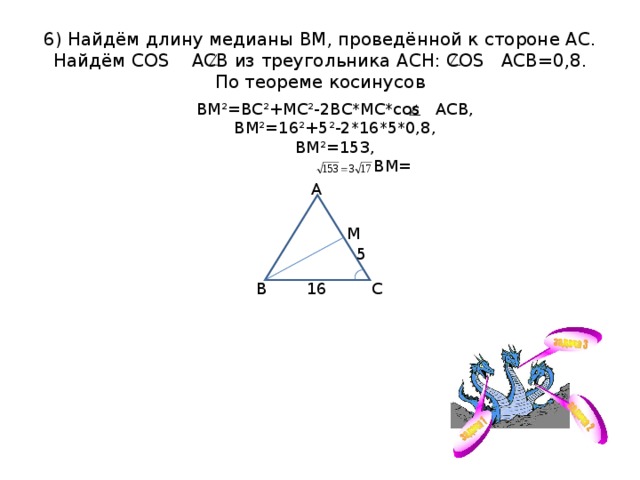
6) Найдём длину медианы ВМ, проведённой к стороне АС. Найдём COS АСВ из треугольника АСН: COS АСВ=0,8. По теореме косинусов

ВМ²=ВС²+МС²-2ВС*МС* cos АСВ,

ВМ²=16²+5²-2*16*5*0,8,

ВМ²=153,

ВМ=

А

М

5

16

С

В

Прямоугольный треугольник ( a- катет, b- катет, с-гипотенуза)

В прямоугольном треугольнике а²+ b²=c² (теорема Пифагора).

Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы: R=

Сумма острых углов прямоугольного треугольника равна 90°.

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Задание 3. Дан прямоугольный треугольник с катетами 6 и 8. Найдите: 1) периметр; 2) площадь; 3) радиус описанного круга; 4) радиус вписанной окружности; 5) тригонометрические функции меньшего угла;

6) высоту, проведённую к гипотенузе; 7) медиану, проведённую к гипотенузе;

8) биссектрису большого угла.

Решение

• Найдём третью сторону (гипотенузу). По теореме Пифагора:

АВ²=АС²+ВС²=8²+6²=64+36=100. АВ =10

Найдём периметр треугольника Р=6+8+10=24.

2) Площадь прямоугольного треугольника равна половине произведения катетов, т.е.

S АВС =

А

8

С

В

6

3) Центр описанной окружности около прямоугольного треугольника является серединой гипотенузы, поэтому радиус описанной окружности равен половине гипотенузы:

R=

4) Радиус вписанной окружности r найдём, используя формулу для площади треугольника S АВС = p*r , где p= . Получим, r=

5) В исходном треугольнике меньшей стороной является катет ВС, поэтому меньшим углом треугольника является угол А.

cos A= , sin A= , tg A= , с tg A=

6) Для нахождения высоты, проведённой к гипотенузе, выразим площадь треугольника через гипотенузу и высоту СН: S АВС = . Зная площадь найдём СН:

СН=

А

8

Н

С

В

6

7) Так как в прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине, то СМ=

8) Для нахождения длины биссектрисы CL прямого угла С, используем свойство биссектрисы угла треугольника:

3 AL=4LB

C другой стороны, AL+LB=10

Решим систему

3 AL=4LB 3(10- LB)=4LB , 7 LB=30

AL=10-LB ; AL=10-LB ; AL=10-LB.

Получим AL= а BL=

По теореме синусов из треугольника CLB :

A

8

L

B

C

6

Параллелограмм Диагонали параллелограмма точкой пересечения делятся пополам. Диагонали параллелограмма делят его на четыре равновеликих треугольника. Противоположные стороны параллелограмма равны и параллельны.

S=ah a , S=ab sin(a , b) , где a и b – смежные стороны параллелограмма, h a – высота, проведённая к стороне а.

Задание 4. Разность углов, прилежащих к одной стороне параллелограмма равна 100°. Найдите углы параллелограмма.

Решение.

• Пусть меньший угол параллелограмма равен х, тогда большой угол равен 100°+х. Так как сумма углов, прилежащих к одной стороне, в параллелограмме равна 180°, то х+100°+х=180° и х=40°.
• Большой угол параллелограмма равен 140°.

Ответ: 40° и 140°.

В

С

100°+x

х

А

D

Задание 5. В параллелограмме ABCD диагонали пересекаются в точке О и АВ=13, AD=14 , BD=15 .

Найдите:

В

С

• площадь; 2) площадь треугольника АВО; 3) высоты параллелограмма.

Решение.

• Параллелограмм разбивается диагональю В D на два треугольника, равных по площади. Площадь треугольника АВ D можно найти по формуле Герона или следующим образом. Рассмотрим треугольник АВ D . Опустим высоту ВТ к стороне AD . Введём обозначения АТ=х, Т D =14-х. С помощью теоремы Пифагора выразим высоту ВТ из двух полученных прямоугольных треугольников:

ВТ²=169-х² и ВТ²=225-(14-х)².

Составим равенство, найдём х, а затем и высоту ВТ.

169-х²=225-(14-х)²,

28х=140, х=АТ=5.

O

13

А

D

14

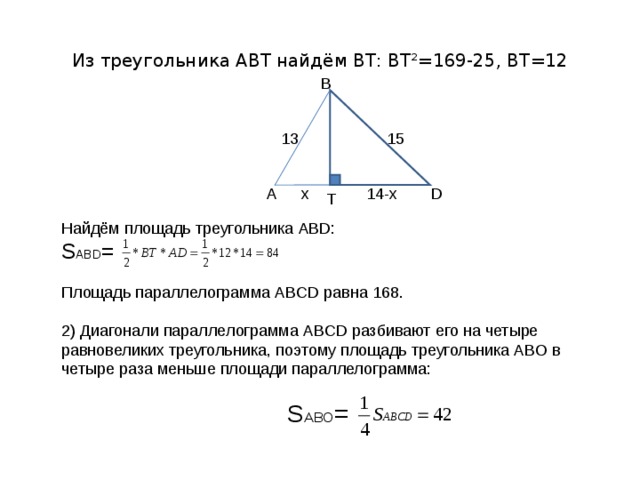
Из треугольника АВТ найдём ВТ: ВТ²=169-25, ВТ=12

В

Найдём площадь треугольника ABD :

S ABD =

Площадь параллелограмма ABCD равна 168.

2) Диагонали параллелограмма ABCD разбивают его на четыре равновеликих треугольника, поэтому площадь треугольника АВО в четыре раза меньше площади параллелограмма:

S ABO =

13

15

А

D

x

14-x

Т

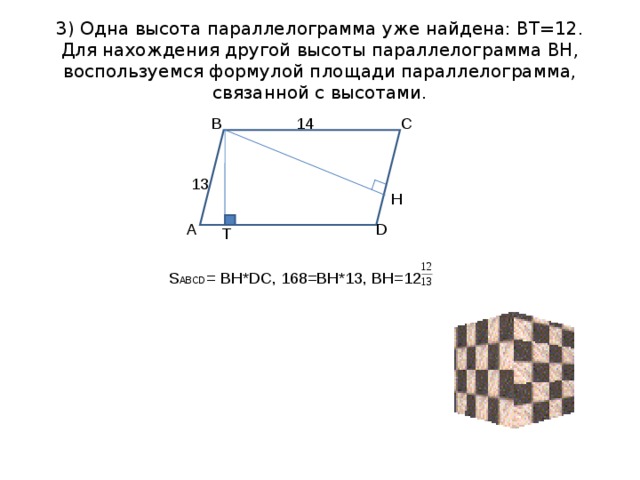
3) Одна высота параллелограмма уже найдена: ВТ=12. Для нахождения другой высоты параллелограмма ВН, воспользуемся формулой площади параллелограмма, связанной с высотами.

В

С

14

13

H

D

А

T

S ABCD = BH*DC , 168= BH*13 , ВН=12

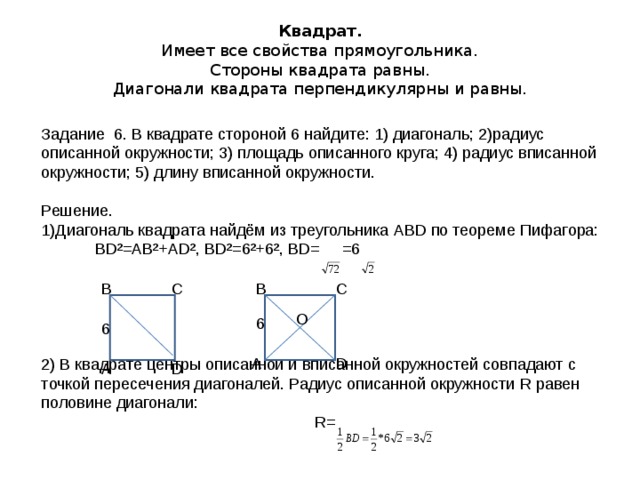
Квадрат. Имеет все свойства прямоугольника. Стороны квадрата равны. Диагонали квадрата перпендикулярны и равны.

Задание 6. В квадрате стороной 6 найдите: 1) диагональ; 2)радиус описанной окружности; 3) площадь описанного круга; 4) радиус вписанной окружности; 5) длину вписанной окружности.

Решение.

• Диагональ квадрата найдём из треугольника ABD по теореме Пифагора:

BD²=AB²+AD² , BD²= 6 ²+ 6 ² , BD= =6

2) В квадрате центры описанной и вписанной окружностей совпадают с точкой пересечения диагоналей. Радиус описанной окружности R равен половине диагонали:

R=

C

B

C

B

O

6

6

A

D

D

A

3) Найдём площадь описанного круга: S= π r²= π *(3 )²= 18 π .

4) Радиус окружности, вписанной в квадрат, равен половине стороны квадрата:

r=

5) Найдём длину вписанной окружности

С=2 π r=2 π *3=6 π .

Трапеция

S= , где a и b – основания трапеции, h – её высота.

Средняя линяя трапеции параллельна основаниям и равна их полусумме.

Дана трапеция ABCD c основаниями AD=16 , BC=2 . Боковые стороны трапеции равны 13 и 15. Диагонали трапеции пересекаются в точке Е. Найдите: 1) среднюю линию трапеции; 2) высоту; 3) площадь.

В

C

E

15

13

D

А

16

Решение.

• Средняя линия трапеции ( L) равна полусумме оснований трапеции:

L=

2) Чтобы найти высоту исходной неравнобедренной трапеции, используем дополнительное построение: проведём отрезок BN , параллельный CD . Отрезок BN разбивает трапецию на две части: BCDN и треугольник ABN . Высота треугольника ABN , опущенная из вершины В, равна высоте исходной трапеции.

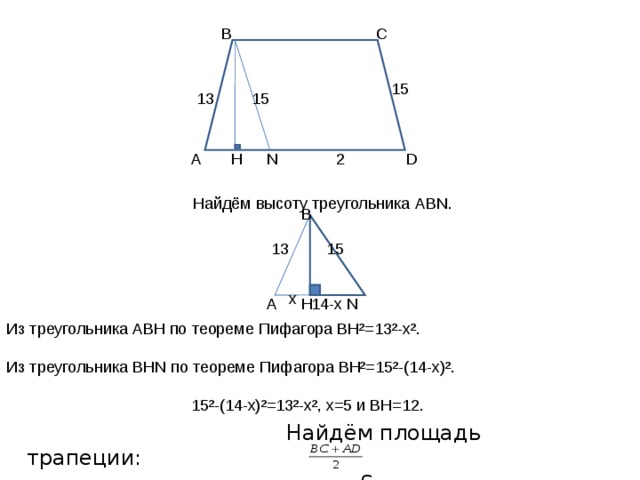
C

B

15

13

15

D

N

2

A

H

Найдём высоту треугольника ABN .

B

13

15

x

A

N

H

14-x

Из треугольника АВН по теореме Пифагора ВН²=13²-х².

Из треугольника BHN по теореме Пифагора ВН²=15²-(14-х)².

15²-(14-х)²=13²-х², х=5 и ВН=12.

Найдём площадь трапеции: S АВС D = *BN=9*12=108

Вписанные углы.

Вписанный угол измеряется половиной дуги,

на которую он опирается.

Вписанный угол,

опирающийся на полуокружность, - прямой.

Задание 7. Центральный угол MON на 50° больше вписанного угла, опирающегося на дугу MN . Найдите каждый из этих углов.

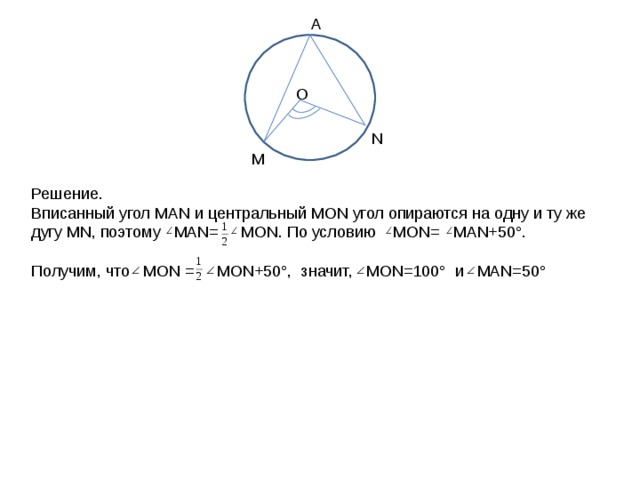
А

O

N

М

Решение.

Вписанный угол MAN и центральный MON угол опираются на одну и ту же дугу MN , поэтому MAN= MON . По условию MON= MAN+50°.

Получим, что MON = MON+50° , значит, MON=100° и MAN=50°

Литература

• Подготовка к ГИА 9 класс, 2013г. В.В.Кочагин, М.Н.Кочагина
• Тематические тренировочные задания 2013г. В.В.Кочагин, М.Н.Кочагина.
• Тренировочные задания 2013г. Т.А Корешкова, В.В.Мирошин, Н.В Шевелева.
• Ященко и др. Три модуля 2013г.