Презентация "Графы"

Графы

Графом на плоскости называется конечное множество точек плоскости , некоторые из которых соединены линиями. Эти точки называют вершинами графа , а соединяющие их линии – ребрами. Примерами графов могут служить любая карта дорог , электросхема , чертеж многоугольника и т.д.

Теория графов возникла в 1736г. , когда Леонард Эйлер опубликовал первую статью о графах.

Эйлера называют идеальным математиком 18 века.

В этом году исполнилось 300 лет со дня рождения Леонарда Эйлера .

ЛЕОНАРД ЭЙЛЕР

Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества. До сих пор школьники всех стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер.

Леонард Эйлер был избран академиком

в восьми странах мира. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Трудно даже перечислить все отрасли, в которых трудился великий учёный. Но в первую очередь он был математиком.

Использует графы и дворянство. На следующем слайде приведена часть генеалогического дерева знаменитого дворянского рода. Здесь его вершины – члены этого рода , а связывающие их отрезки - отношения родственности , ведущие от родителей к детям.

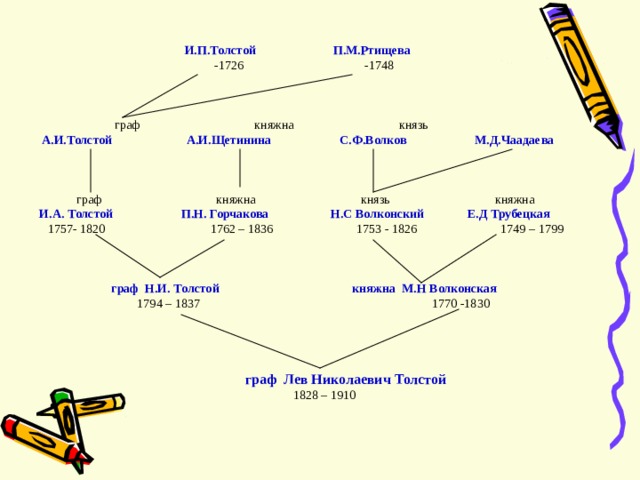
И.П.Толстой П.М.Ртищева

-1726 -1748

граф княжна князь

А.И.Толстой А.И.Щетинина С.Ф.Волков М.Д.Чаадаева

граф княжна князь княжна

И.А. Толстой П.Н. Горчакова Н.С Волконский Е.Д Трубецкая

1757- 1820 1762 – 1836 1753 - 1826 1749 – 1799

граф Н.И. Толстой княжна М.Н Волконская

1794 – 1837 1770 -1830

граф Лев Николаевич Толстой

1828 – 1910

А началась теория графов с разбора широко известной теперь задачи о кенигсбергских мостах. Различные части города были соединены семью мостами , как показано на рисунке.

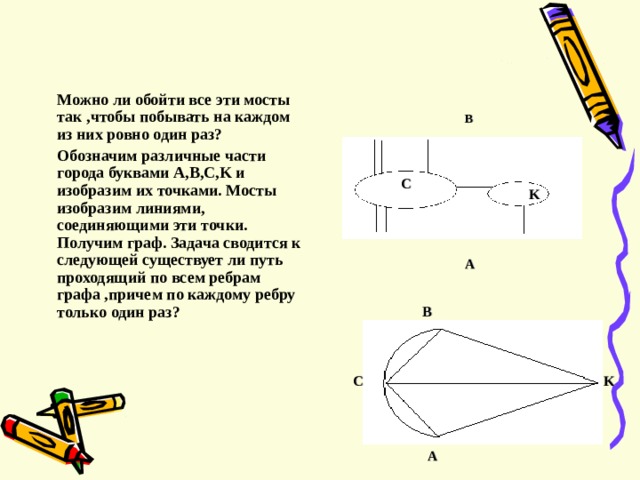
Можно ли обойти все эти мосты так , чтобы побывать на каждом из них ровно один раз ?

Обозначим различные части города буквами A,B,C,K и изобразим их точками. Мосты изобразим линиями , соединяющими эти точки. Получим граф. Задача сводится к следующей существует ли путь проходящий по всем ребрам графа , причем по каждому ребру только один раз ?

B

C

K

A

B

С

K

A

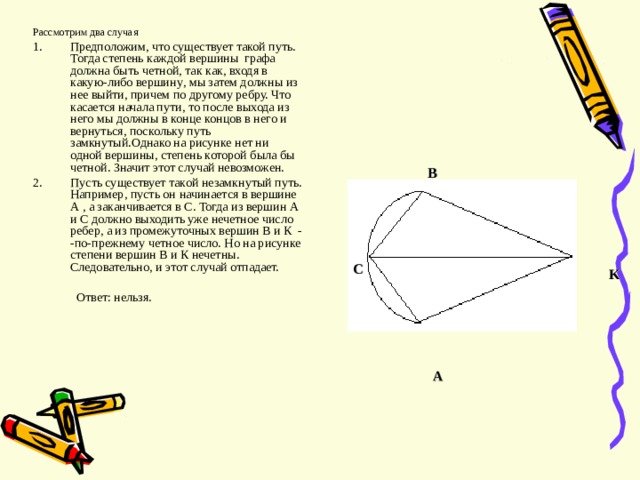
Рассмотрим два случая

• Предположим , что существует такой путь. Тогда степень каждой вершины графа должна быть четной , так как , входя в какую-либо вершину , мы затем должны из нее выйти , причем по другому ребру. Что касается начала пути , то после выхода из него мы должны в конце концов в него и вернуться , поскольку путь замкнутый.Однако на рисунке нет ни одной вершины , степень которой была бы четной. Значит этот случай невозможен.
• Пусть существует такой незамкнутый путь. Например , пусть он начинается в вершине А , а заканчивается в С. Тогда из вершин А и С должно выходить уже нечетное число ребер , а из промежуточных вершин В и К - -по-прежнему четное число. Но на рисунке степени вершин В и К нечетны. Следовательно , и этот случай отпадает.

Ответ : нельзя.

B

С

K

A

Решая задачу о кенигсбергских мостах , Эйлер установил свойства графа , которые я рассмотрел в работе.

1.Если существует замкнутый путь, проходящий по всем ребрам графа, причем по каждому ребру только один раз, то степени всех вершин графа четные.

2. Если существует аналогичный незамкнутый путь, то степени начала и конца пути нечетные , а остальных вершин – четные.

Решение некоторых задач , представленных в работе я хочу показать.

Задача 1.

Можно ли обвести карандашом , не отрывая его от бумаги и не проходя по одной линии дважды правильный пятиугольник с диагоналями ?

Ответ : можно , так как по Эйлеру степени начала и конца пути нечетные , а остальных вершин – четные.

Задача 2.

Исходя из четности и нечетности вершин графа можно показать какие из букв русского алфавита можно нарисовать одним росчерком ?

Ответ : Б В Г З И Л М О П Р С Ф Ъ Я.

Задача 3.

В первенстве класса по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной, Еленой; Борис – с Андреем, Галиной; Виктор – с Галиной, Дмитрием, Еленой; Галина – с Андреем, Виктором и Борисом. Сколько игр проведено к настоящему моменту и сколько ещё осталось?

Построим граф (рис.)

Сыграно семь игр ( черный цвет ребер).

На рисунке граф имеет 8 ребер (красный цвет ребер) , следовательно , осталось провести 8 игр.

Задача 4.

В школьном драматическом кружке решили ставить гоголевского “ Ревизора “ . И тут разгорелся жаркий спор. Все началось с Ляпкина- Тяпкина.

-Ляпкиным- Тяпкиным буду я ! - решительно заявил Дима.- С раннего детства я мечтал воплотить этот образ на сцене.

• Ну хорошо, согласен уступить эту роль, если мне дадут сыграть Хлестакова,- проявил великодушие Гена.
• А мне – Осипа, -не уступил ему в великодушии Дима.
• Хочу быть Земляникой или Городничим, -сказал Вова.
• Нет, Городничим буду я,- хором закричали Алик и Боря. – Или Хлестаковым,- добавили они одновременно.

Удастся ли распределить роли так, чтобы исполнители были довольны ?

Построим граф для ситуации, описанной в задаче.

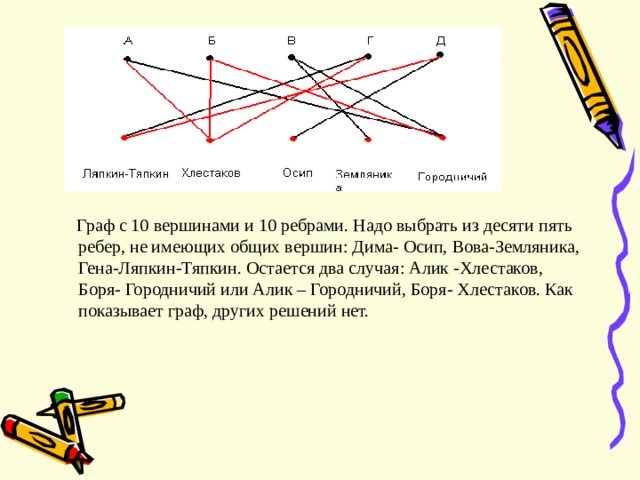
Граф с 10 вершинами и 10 ребрами. Надо выбрать из десяти пять ребер, не имеющих общих вершин : Дима- Осип, Вова-Земляника, Гена-Ляпкин-Тяпкин. Остается два случая : Алик -Хлестаков, Боря- Городничий или Алик – Городничий, Боря- Хлестаков. Как показывает граф, других решений нет.

Задача 5.

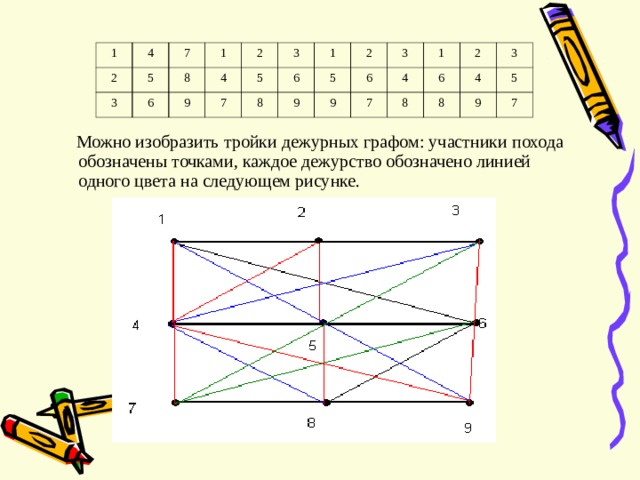
В походе, который длился 12 дней, участвовали 9 человек. Каждый день дежурили 3 человека. При этом дежурные ссорились друг с другом, и никакие двое из них не хотели больше ни разу дежурить вместе. Тем не менее участники похода утверждают, что все 12 дней им удавалось назначать тройки дежурных с учетом этого требования. Могло ли так быть ?

Участники похода обозначены цифрами от 1 до 9, каждый столбец соответствует тройке дежурных.

1

4

2

3

7

5

8

6

1

2

4

9

5

7

3

8

1

6

9

2

5

9

6

3

1

4

7

6

2

8

4

3

8

5

9

7

Можно изобразить тройки дежурных графом : участники похода обозначены точками, каждое дежурство обозначено линией одного цвета на следующем рисунке.

Графы достаточно широко применяются в математике, технике, экономике, управлении. Знание основ теории графов необходимо в различных областях, связанных с управлением производством, бизнесом. Кроме того, выполняя эту работу, я усвоил начальные азы при работе в текстовом редакторе WORD , презентацией POWER POINT .