Министерство Образования и науки Республики Казахстан
Управление образования Карагандинской области
КГУ «Темиртауский профессионально-технический колледж»
Доклад
«Математические диктанты,
как средство активизации мыслительной деятельности студентов»
Подготовила: Созинова Л.З.-
преподаватель математики
г.Темиртау
2016 г
Математические диктанты — хорошо известная форма контроля знаний. Преподаватель сам или с помощью звукозаписи задает вопросы, студенты записывают под номерами краткие ответы на них. Как правило, студентам трудно воспринимать задания на слух. Но если диктанты проводить часто, то они овладевают этим навыком. А ценность такого умения неоспорима. Иногда слуховому восприятию нужно помочь. Для этого одновременно с чтением показываю его на плакате. В зависимости от подготовленности студентов число заданий увеличиваю или уменьшаю.
Задача преподавателя - сделать урок более продуктивным, активизировать студентов, улучшить индивидуальную работу в процессе обучения.
Математический диктант может заменить опрос по теме, заданной для повторения. Его продолжительность обычно 10–15 минут.
Он представляет собой систему вопросов, связанных между собой. Прежде всего, они помогают контролировать знания, умения и навыки учащихся. Проанализировав диктанты, преподаватель получает достаточно подробную информацию об уровне усвоения пройденного как отдельными студентами, так и группой в целом. Это позволяет оперативно устранять пробелы в подготовке студентов. Однако ещё более важно то, что математические диктанты играют обучающую роль. Выслушав фразу диктанта, студенты выполняют определенную работу – записывают алгебраическое выражение (равенство, неравенство, формулу), выполняют указанное построение. При этом требуется не только воспроизвести заученную формулировку, а творчески подойти к заданию. Диктанты способствуют и развитию навыков логического мышления, и выработке умения работать с чертежными инструментами. При составлении математических диктантов соблюдается принцип "От простого к сложному".
При решении 1-3 заданий слабым учащимся может быть оказана индивидуальная помощь в виде:
а) алгоритма решения, записанного в общем виде;
б) примера-образца;
в) карточки-консультации.
4 задание решается по правилу или алгоритму, воспроизводимому по памяти.
5 задание требует от учащегося применения знаний в проблемной или нестандартной ситуации, самостоятельного конструирования нового алгоритма на основе ранее изученных.
Разноуровневые задания позволяют включить в посильную работу весь класс, способствуют формированию познавательного интереса к занятиям математикой.
Условия эффективности: понимание учащимися структуры диктанта, умение адекватно оценить свои учебные возможности и рационально организовать свою деятельность при выполнении математического диктанта.
Виды диктантов
Математические диктанты можно разделить на следующие виды: проверочные, обзорные, итоговые. Каждый вид математических диктантов имеет свои особенности, свои цели, и следовательно, требования, предъявляемые к составлению этих работ, должны быть различны.
Проверочные диктанты предназначены для контроля усвоения отдельного фрагмента курса в период изучения темы. При их выполнении учитель своевременно получает информацию о том, как усваивается тема, что позволяет ему вовремя выявить ошибки, обнаружить плохо усвоивших тот или иной материал и в зависимости от этого строить работу по изучению данной темы. Учащиеся же получают дополнительную практику в самостоятельном решении задач и тем самым готовятся к контрольной работе по данной теме. Поскольку проверочные диктанты проводятся после отработки основных умений и навыков, то в них включаются задания не только репродуктивного характера. Основа проверочных диктантов — задания реконструктивного характера. В то же время в проверочные диктанты не следует включать задания сложнее тех, которые выполнялись учащимися на уроках и дома.
Известная не шаблонность постановки задачи и ограниченность времени на выполнение задания дисциплинируют студентов, приучают к собранности, сосредоточенности, целеустремленности.
Проведение математических диктантов способствует и повышению общей грамотности студентов. Опыт показывает, что в результате систематического использования этой формы работы резко уменьшается количество ошибок в написании математических терминов.
Математические диктанты являются одной из форм письменной работы. В зависимости от текста он проводится 8-15 минут. Поэтому проводить его следует либо в начале урока, либо в конце.
Способы проведения диктантов
Текст диктанта может быть:
а) спроецирован на доску с помощью компьютера;
б) зачитан учителем;
в) воспроизведен с помощью звукозаписи;
г) показан на плакате
Как организовать проведение математического диктанта.
Для диктантов лучше использовать листы бумаги (бланки ответов). Можно использовать при проведении диктанта два бланка ответов для того, чтобы ученик мог один бланк сдать учителю, а второй использовать для проверки правильности выполнения работы. Если есть закрытые доски, то можно, либо написать ответы заранее, либо вызвать студентов к доске и их ответы проверить вместе с группой. Опять же можно использовать интерактивную доску. Проверка сразу на уроке даёт возможность ещё раз закрепить изученный материал. Кроме того, выполнив любой вид работы, каждый студент жаждет быстрее узнать результаты своей работы и оценку за неё. Вспомните: после контрольных, самостоятельных работ сколько раз вы слышали эту фразу “я уже сдал тетрадь, а покажите, какой там ответ или как это решается”? Если диктант проводится сразу после изучения нового материала, то можно проверить ответы, обсудить результаты, а отметки выставлять только “4” или “5”.
Организация проверки
Обычный способ проверки, когда ответы студентов учитель собирает и проверяет дома, малоэффективен: студент жаждет узнать результаты своей работы непосредственно после завершения, на следующий день они его интересуют уже меньше. Поэтому организовать проверку можно, например, так: учитель записывает на доске правильные ответы.
Весьма важно обучить студентов правильной проверке своих математических диктантов. Иначе некоторые просто не замечают допущенных ошибок. Можно предложить им самостоятельно оценивать результаты диктанта по указанным критериям.
Вот возможная шкала оценок для диктантов различной длины.
| Число вопросов | 5 | 6 | 7 | 8 | 9 | 10 | |||||||||||||||||
| Число верных ответов | 3 | 4 | 5 | 4 | 5 | 6 | 4, 5 | 6 | 7 | 5, 6 | 7 | 8 | 5, 6 | 7, 8 | 9 | 6, 7 | 8, 9 | 10 | |||||
| Отметка | 3 | 4 | 5 | 3 | 4 | 5 | 3 | 4 | 5 | 3 | 4 | 5 | 3 | 4 | 5 | 3 | 4 | 5 | |||||
Разумеется, преподаватель может – исходя из особенностей студентов группы, педагогической целесообразности – использовать свои подходы к оцениванию результатов диктанта. Иногда вопросы диктанта по значимости и содержанию можно разделить на “лёгкие” и “трудные”. В этом случае есть смысл каждый вопрос оценить в баллах (например, от 1 до 3 баллов), тогда итоговая оценка выставляется по сумме баллов.
Приведу несколько примеров математических диктантов.
ИМЕННОЙ ДИКТАНТ
«Назови знак»
1.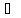
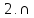
3.
4.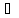
5.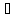
6.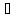
7.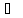
8.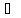
9.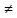
10.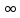
НЕМОЙ ДИКТАНТ
Показывается плакат с заданием, студенты выполняют его.
Решите показательные уравнения:
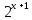 = 32
= 32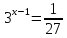
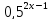 = 0,25
= 0,25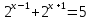
3х + 2 + 3х = 90.
ОТКРЫТЫЙ ДИКТАНТ
«Продолжи предложение»
1. Раздел геометрии изучающий фигуры в пространстве называется…..
2.Основными понятиями стереометрии являются ……
3.Если 2 прямые лежат в одной плоскости и не пересекаются , то они называются….
4.Если 2 прямые имеют одну общую точку , то они называются….
5.Если 2 прямые не пересекаются и не параллельны, то они называются…..
6.Если 2 прямые параллельны 3-ей прямой , то они……
7.Через любые 3 точки, не принадлежащие одной прямой, можно провести….
8.Если 2 различные плоскости имеют общую точку, то они
пересекаются …..
9.Через 2 пересекающиеся плоскости можно провести….
10. Если 2 точки прямой лежат в плоскости, то и вся прямая….
ЦИФРОВОЙ ДИКТАНТ
Верно ли , что решением этого неравенства 3(2х+1)
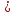 15
15
является промежуток (2;∞) ?
Верно ли, что решением этого неравенства 4(х-2)
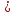 12
12
является промежуток (-∞; 5) ?
Верно ли, что решением этого неравенства 5( 3х-1) ≥ 2(х-2) служит промежуток (6;∞) ?
Верно ли, что ответом этого неравенства - 2(х-2)
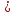 8 служит промежуток ( -2;∞) ?
8 служит промежуток ( -2;∞) ?Верно ли, что решением этого неравенства -
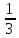 х
х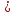 6 является промежуток (-∞;18) ?
6 является промежуток (-∞;18) ?
Студенты записывают ответ либо словом «ДА», либо «НЕТ»
Далее преподаватель просит напротив слова «ДА» поставить цифру «1», а напротив слова «НЕТ – цифру «0».Затем надо выписать последовательность единиц и нулей по порядку. У преподавателя есть ключ к ответам : 11010.
Остается проверить диктант и выставить оценки.
Рекомендуемая литература
1. Арутюнян Е.Б., Волович М.Б., Глазков Ю.А., Левитас Г.Г. Математические диктанты для 5–9 классов. — М.: Просвещение, 1991.
2. Афанасьева Т.Л., Тапилина Л.А. Геометрия. 9 класс. (Пособие для учителя к учебнику Л.С. Атанасяна, и др. «Геометрия. 7–9 классы»). — Волгоград: Учитель, 2007.
3. Барышникова Н.В. Математика. 5–11 классы. Нестандартные уроки. — Волгоград: Учитель, 2007.
4. Груденов Я.И. Совершенствование методики работы учителя математики. — М.: Просвещение, 1990.
5. Ершова А.П., Голобородько В.В. Устные проверочные и зачетные работы по геометрии для 7– 9 классов. — М.: Илекса, 2004.
6. Есипов Б.П. Самостоятельная работа учащихся на уроках. — М., 1961.
7. Зив Б.Г., Алтынов П.И. Алгебра и начала анализа. Геометрия. 10–11 классы. Учебно-методическое пособие. — М., 1999.
8. Лебедев П.М. Понятие познавательной активности учащихся и пути ее измерения//Радянська школа, 1970, № 9.
9. Левитас Г.Г. Диктанты по алгебре. 7– 11 классы. Дидактические материалы. — М.: Илекса, 2005.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Преподаватель математики (26.88 KB)
Преподаватель математики (26.88 KB)
 0
0 579
579 16
16 Нравится
0
Нравится
0



