Математика выявляет порядок, симметрию и определенность, а это – важнейшие виды прекрасного».
Аристотель
Цели урока:
-сформулировать определение средней линии трапеции;
-сформулировать и доказать свойства средней линии трапеции,
-учиться применять их при решении задач.
План выхода из затруднения
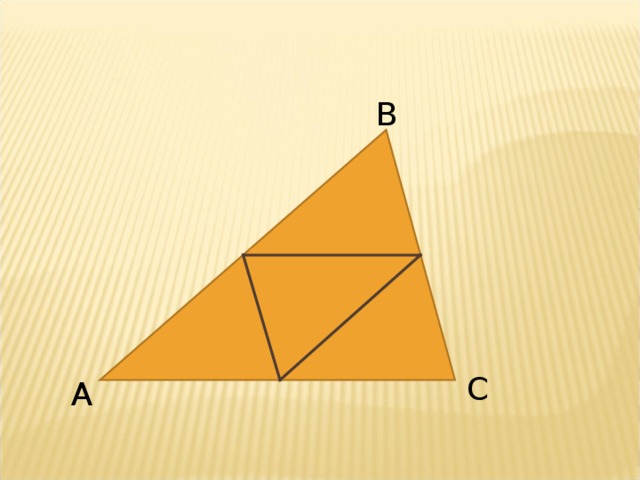
1) Выяснить, что может называться средней линией трапеции.
2) Сформулировать предполагаемые свойства средней линии трапеции.
3) Доказать свойства средней линии трапеции.
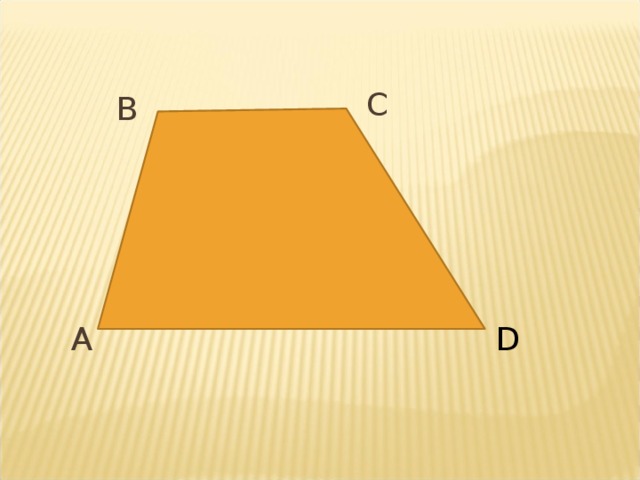
Теорема.
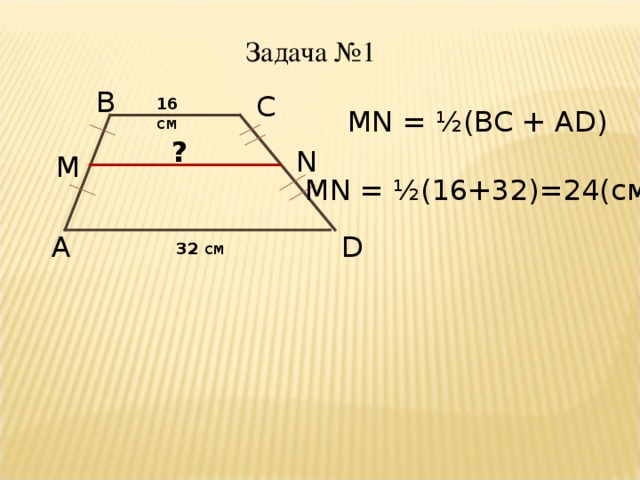
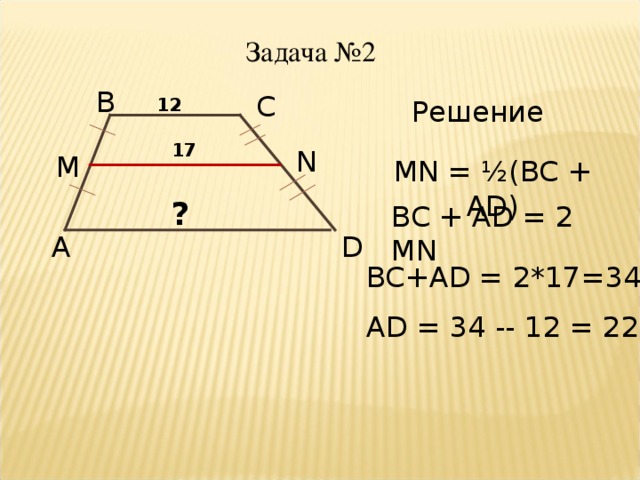
Средняя линия трапеции параллельна основаниям и равна их полусумме.

 Получите свидетельство
Получите свидетельство Вход
Вход


















 Презентация "Средняя линия трапеция" (1.59 MB)
Презентация "Средняя линия трапеция" (1.59 MB)
 0
0 1366
1366 160
160 Нравится
0
Нравится
0


