


Это случилось на берегу Планиметрического моря в городе Плоских фигур.

Милая добрая Трапеция ABCD потеряла свою площадь, а это было её наследство, оставленное старым дядюшкой Параллелограммом .
Недолго горевала
Трапеция , решила она подать
заявление во все частные сыскные агентства, существующие в городе Плоских фигур.

Его владелицы две пожилые дамы Алгебра и Тригонометрия . Служат у них молодые, энергичные детективы Квадратный корень , Синус , Косинус .
Они стали узнавать у Трапеции , а что же она может рассказать о себе.
Cos
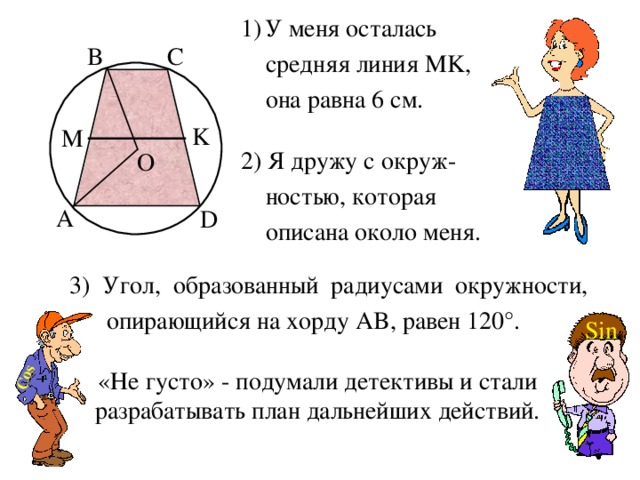
средняя линия MK ,
она равна 6 см.
2) Я дружу с окруж-
ностью, которая
описана около меня.
C
B
K
M
O
A
D
3) Угол, образованный радиусами окружности,
опирающийся на хорду AB , равен 120 ° .
Sin
«Не густо» - подумали детективы и стали разрабатывать план дальнейших действий.

Около трапеции со средней линией 6 см описана окружность. Угол между радиусами окружности, проведенными к концам боковой стороны, равен 120 ° . Найдите площадь трапеции.

ВПИСАННЫЙ УГОЛ
А между тем Трапеция отправилась во второе частное агентство «Вписанный угол».
Его владельцы – два брата. Молодые красавцы Вписанные углы , равные 30 °.

Только взглянув на Трапецию , они тут же сообразили, что трапеция так хорошо сложена, и не трудно будет доказать, что она равнобокая, а её подружка окружность им в этом поможет.

Поворот
Пока озадаченные Вписанные углы решали эту проблему, Трапеция пришла в третье сыскное агентство под названием «Поворот».
Им владел почтенный старец Поворот .
Вектор BC служил у него детективом .
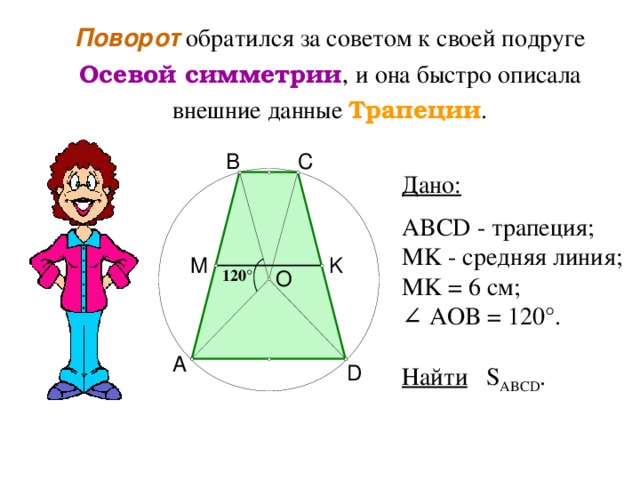
Поворот обратился за советом к своей подруге Осевой симметрии , и она быстро описала внешние данные Трапеции .
C
B
Дано:
ABCD - трапеция;
MK - средняя линия;
MK = 6 см;
∠ AOB = 120 °.
Найти S ABCD .
K
M
120 °
O
A
D
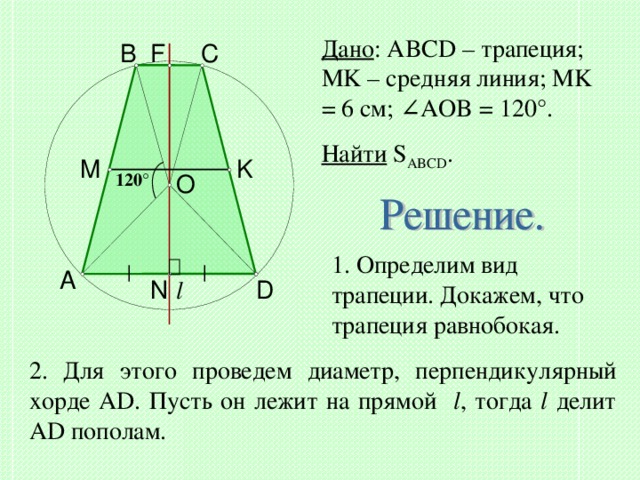
Дано : ABCD – трапеция; MK – средняя линия; MK = 6 см; ∠ AOB = 120 °.
Найти S ABCD .
F
C
B
M
K
120 °
O
1. Определим вид трапеции. Докажем, что трапеция равнобокая.
A
l
N
D
2. Для этого проведем диаметр, перпендикулярный хорде AD . Пусть он лежит на прямой l , тогда l делит AD пополам.
F
B
C
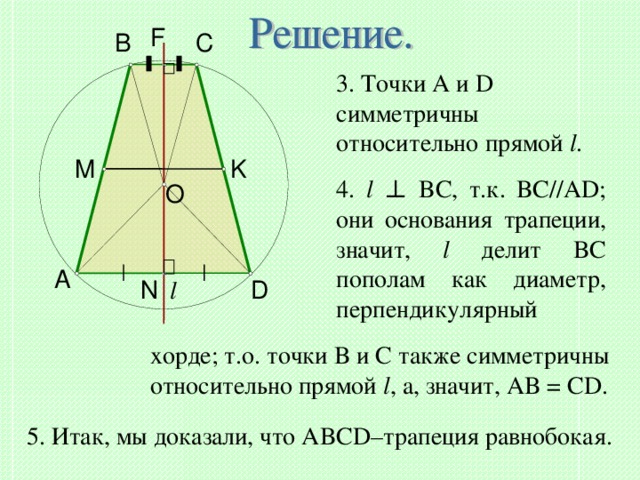
3. Точки A и D симметричны относительно прямой l .
M
K
4. l ⊥ BC , т.к. BC//AD ; они основания трапеции, значит, l делит BC пополам как диаметр, перпендикулярный
O
A
l
N
D
хорде; т.о. точки B и C также симметричны относительно прямой l , а, значит, AB = CD.
5. Итак, мы доказали, что ABCD– трапеция равнобокая.

Поворот
Sin
Все детективы справились с этой задачей, и теперь пути поиска площади Трапеции в каждом агентстве разошлись.
B
C
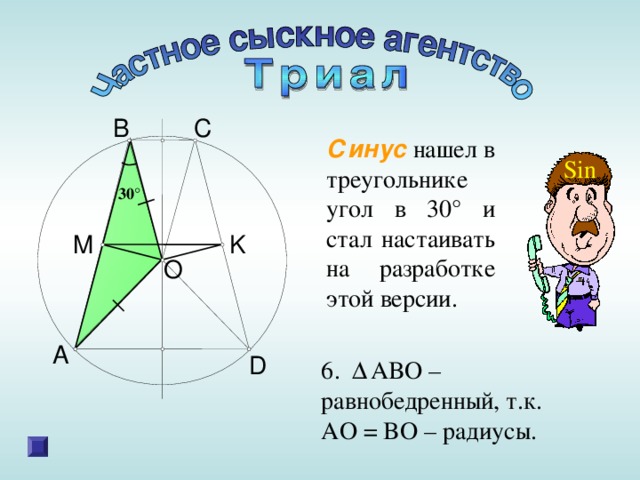
Синус нашел в треугольнике угол в 30 ° и стал настаивать на разработке этой версии.
Sin
30 °
K
M
O
A
D
6 . Δ ABO – равнобедренный, т.к. AO = BO – радиусы.
2x
B
C
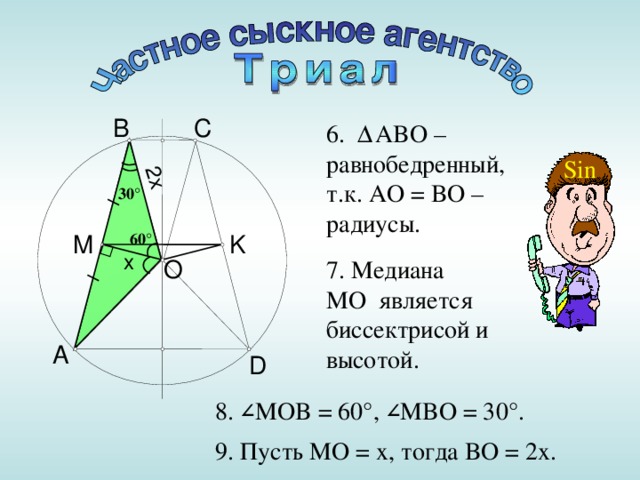
6 . Δ ABO – равнобедренный, т.к. AO = BO – радиусы.
Sin
30 °
M
K
6 0 °
x
O
7 . Медиана MO является биссектрисой и высотой.
A
D
8 . ∠ MOB = 60°, ∠ MBO = 30°.
9 . Пусть MO = x, тогда BO = 2 x.

Cos
Агентство «Триал» все задачи решает путем введения переменной, исходя из данных условий, оно составляет уравнение.
C
B
α
60 °
60 °
M
K
O
Квадратный корень и Косинус решили объединить свои усилия и рассмотреть треугольник MOK .
A
D
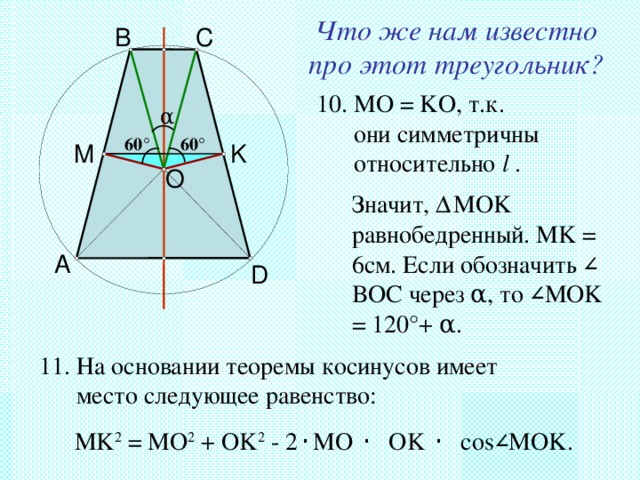
Что же нам известно про этот треугольник?
B
C
10. MO = KO , т.к.
они симметричны
относительно l .
α
60 °
60 °
M
K
O
Значит, Δ MOK равнобедренный. MK = 6см. Если обозначить ∠ BOC через α , то ∠ MOK = 120 ° + α .
A
D
11. На основании теоремы косинусов имеет
место следующее равенство:
MK 2 = MO 2 + OK 2 - 2 · MO · OK · cos ∠ MOK.
cos
x
x
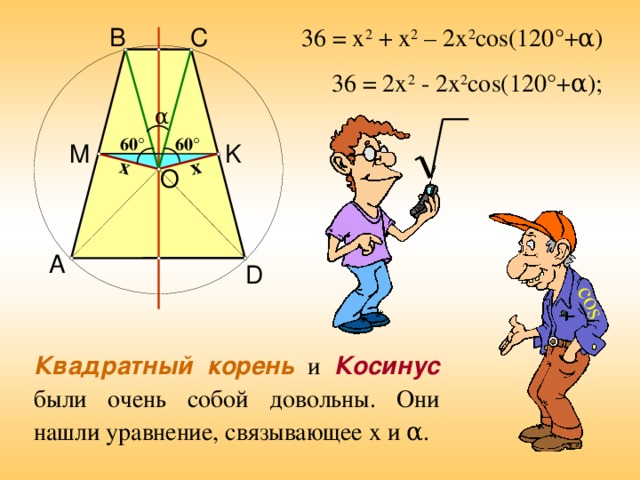
36 = x 2 + x 2 – 2x 2 cos(120 °+ α )
C
B
36 = 2x 2 - 2x 2 cos(120 °+ α );
α
60 °
60 °
M
K
O
A
D
Квадратный корень и Косинус были очень собой довольны. Они нашли уравнение, связывающее x и α .

Cos
Sin
Детектив Синус резко раскритиковал это уравнение. В нем две неизвестные величины. Как же его решить?
А детектив Косинус его успокаивал: «Ничего, ничего, сейчас я найду косинус суммы, и посмотрим, что из этого выйдет».

c о s( α + β ) = cos α cos β – sin α sin β
36 = 2x 2 – 2x 2 (cos120 °cos α – sin120 °sin α );
36 = 2x 2 – 2x 2 (cos(180 °- 60°)cos α – sin60 °sin α );
sin(180 – α ) = sin α
36 = 2x 2 – 2x 2 (- cos α - sin α );
cos(180 ° - α ) = -cos α
36 = 2 x 2 + x 2 cos α + x 2 sin α ;
36 = x 2 (2 + cos α + sin α );

Около нее все время находились равнобедренные треугольники. Они что-то знают. Может быть даже это они похитили площадь Трапеции. Надо их допросить.
Детектив Синус старательно изучал круг знакомств нашей Трапеции.
Sin
2x
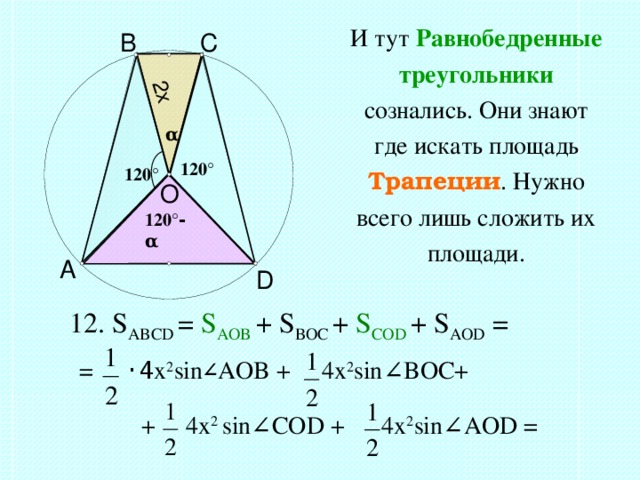
И тут Равнобедренные треугольники сознались. Они знают где искать площадь Трапеции . Нужно всего лишь сложить их площади.
B
C
α
120 °
120 °
O
120 ° - α
A
D
12. S ABCD = S AOB + S BOC + S COD + S AOD =
= ·4 x 2 sin ∠ AOB + 4x 2 sin ∠ BOC+
+ 4x 2 sin ∠ COD + 4x 2 sin ∠ AOD =
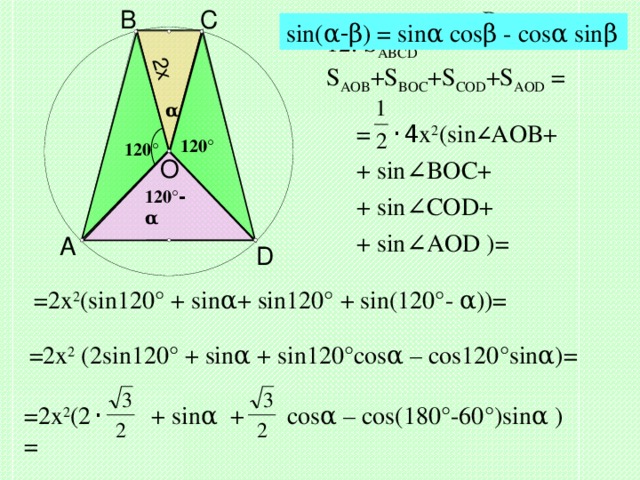
Решение.
C
B
2x
sin( α - β ) = sin α cos β - cos α sin β
12. S ABCD = S AOB +S BOC +S COD +S AOD =
α
= ·4 x 2 (sin ∠ AOB+
+ sin ∠ BOC+
+ sin ∠ COD+
+ sin ∠ AOD ) =
120 °
120 °
O
120 ° - α
A
D
=2x 2 (sin120 ° + sin α + sin120° + sin(120°- α ))=
=2x 2 (2sin120 ° + sin α + sin120°cos α – cos120°sin α )=
=2x 2 (2 · + sin α + cos α – cos(180 °-60°)sin α )=

=2x 2 (2 · + sin α + cos α – cos(180 °-60°)sin α )=
= 2x 2 ( + sin α + cos α + sin α ) =
=x 2 (2 + 2sin α + cos α + sin α ) =
=x 2 (2 + 3sin α + cos α ) = x 2 ( 2 + sin α + cos α )=
√ 3(2+√3sin α + cos α )
(см 2 ).
= 36 .

Детективы частного сыскного агентства Триал отчитались перед Трапецией в письменном виде, предоставив ей свои математические расчеты.
36
F
C
B
E
K
M
O
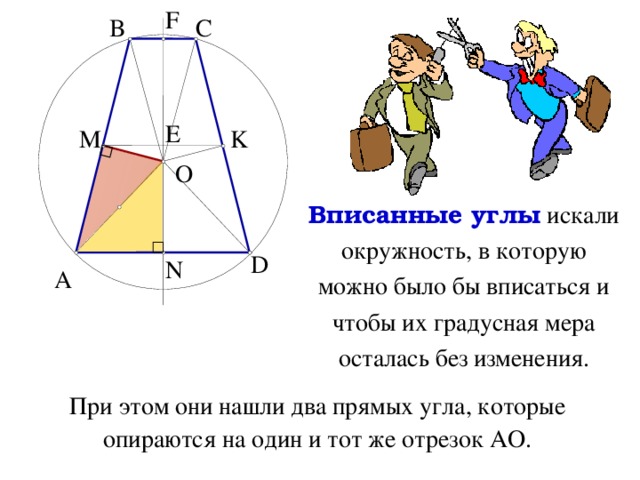
Вписанные углы искали окружность, в которую можно было бы вписаться и чтобы их градусная мера осталась без изменения.
D
N
A
При этом они нашли два прямых угла, которые опираются на один и тот же отрезок AO.
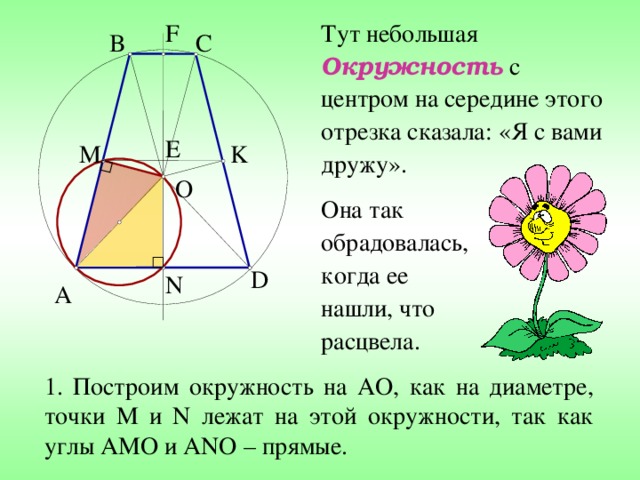
Тут небольшая Окружность с центром на середине этого отрезка сказала: «Я с вами дружу».
F
C
B
E
M
K
O
Она так обрадовалась, когда ее нашли, что расцвела.
D
N
A
1. Построим окружность на AO , как на диаметре, точки M и N лежат на этой окружности, так как углы AMO и ANO – прямые.
F
C
B
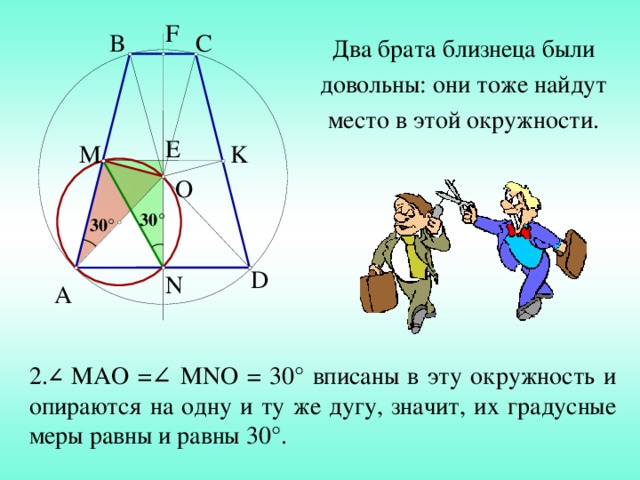
Два брата близнеца были довольны: они тоже найдут место в этой окружности.
E
K
M
O
30 °
30 °
D
N
A
2. ∠ MAO =∠ MNO = 30 ° вписаны в эту окружность и опираются на одну и ту же дугу, значит , их градусные меры равны и равны 30 ° .
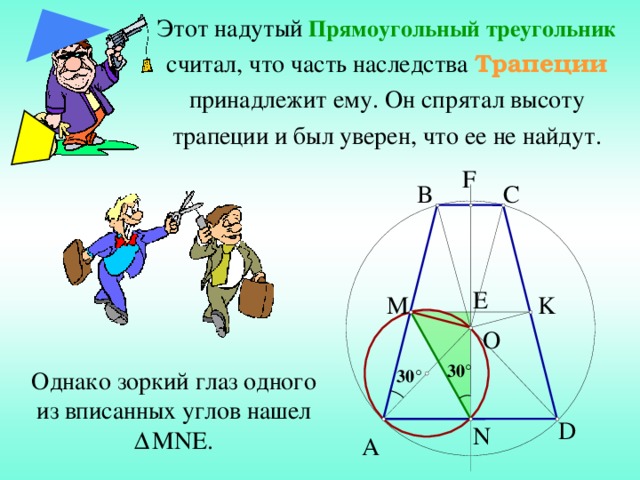
Этот надутый Прямоугольный треугольник считал, что часть наследства Трапеции принадлежит ему. Он спрятал высоту трапеции и был уверен, что ее не найдут.
F
C
B
E
M
K
O
30 °
30 °
Однако зоркий глаз одного из вписанных углов нашел Δ MNE.
D
N
A
F
6 c м
B
C
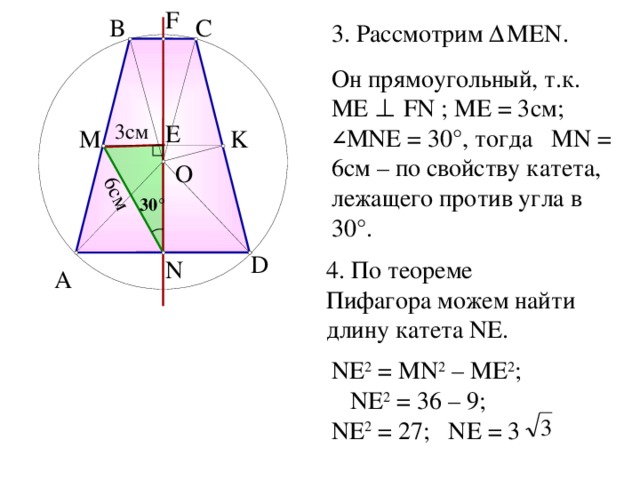
3. Рассмотрим Δ MEN.
Он прямоугольный, т.к. МЕ ⊥ FN ; ME = 3 см ; ∠ MNE = 30°, тогда MN = 6см – по свойству катета, лежащего против угла в 30 ° .
3c м
E
K
M
O
30 °
D
4. По теореме Пифагора можем найти длину катета NE.
N
A
NE 2 = MN 2 – ME 2 ; NE 2 = 36 – 9; NE 2 = 27; NE = 3
F
B
C
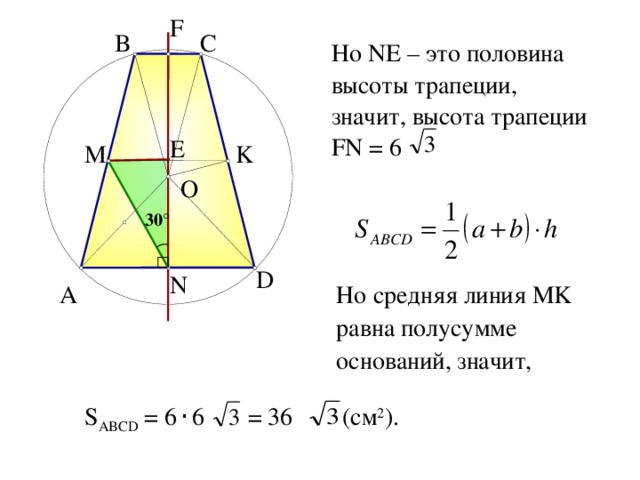
Но NE – это половина высоты трапеции, значит , высота трапеции FN = 6
E
K
M
O
30 °
D
N
A
Но средняя линия MK равна полусумме оснований, значит,
S ABCD = 6 · 6 = 36 (см 2 ).



В городе Плоских фигур живет мисс Овиз , которая всё про всех знает.

Однажды мисс Овиз , она же хорошая знакомая Параллелограмма , познакомилась с Трапецией и узнала о её проблеме.

Мисс Овиз никогда не расставалась со своей записной книжкой, где можно найти информацию о многих жителях города Плоских фигур.
Она вспомнила, что знает одного из предполагаемых наследников Параллелограмма . Возможно он, войдя в доверие к средней линии, украл высоту Трапеции .

Это был Прямоугольный треугольник, один из катетов которого, равен средней линии.
B
C
Мисс Овиз тут же пошла по его следу.
K
M
120 °
O
D
A
L
H
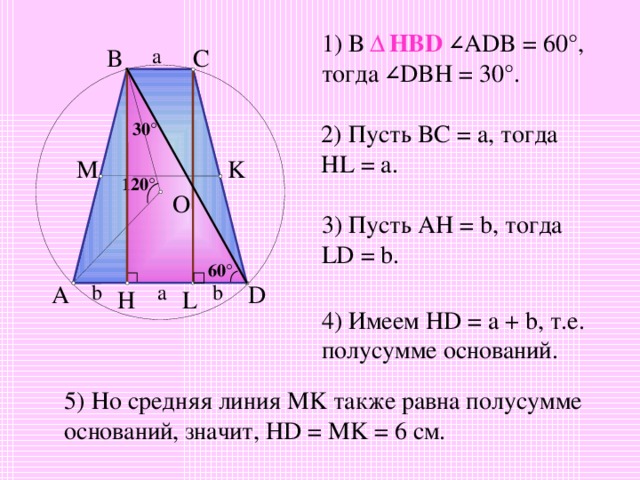
1) В Δ HBD ∠ ADB = 60°, тогда ∠ DBH = 30°.
B
C
a
2) Пусть BC = a, тогда HL = a.
3 0 °
M
K
120 °
O
3) Пусть AH = b, тогда LD = b.
60 °
D
a
b
b
A
H
L
4) Имеем HD = a + b, т.е. полусумме оснований.
5) Но средняя линия MK также равна полусумме оснований, значит, HD = MK = 6 см.
12см
C
B
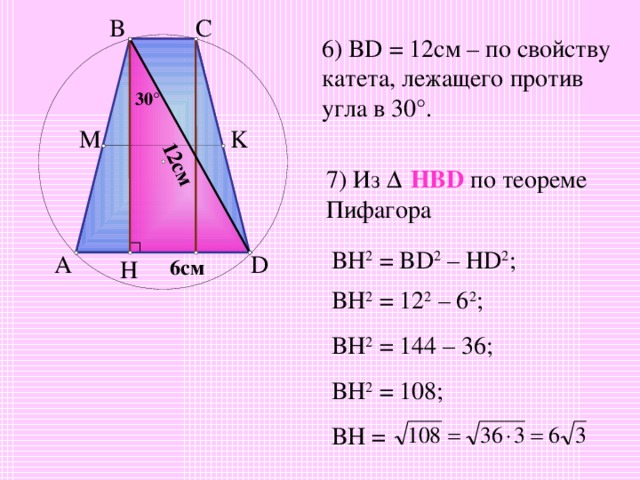
6) BD = 12 см – по свойству катета, лежащего против угла в 30 ° .
3 0 °
M
K
7) Из Δ HBD по теореме Пифагора
BH 2 = BD 2 – HD 2 ;
D
A
H
6 см
BH 2 = 12 2 – 6 2 ;
BH 2 = 144 – 36;
BH 2 = 108;
BH =
C
B
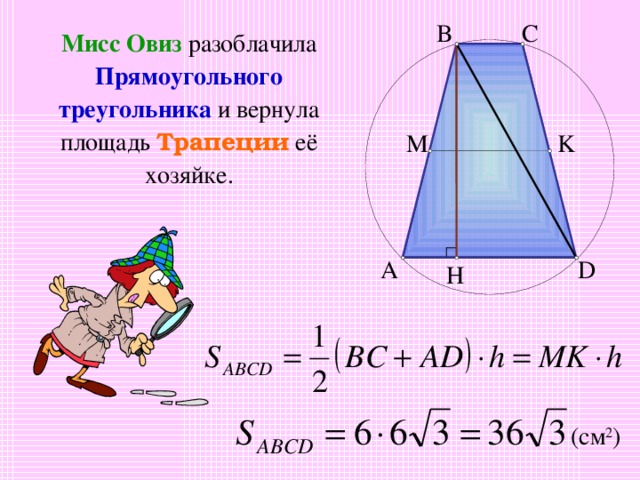
Мисс Овиз разоблачила Прямоугольного треугольника и вернула площадь Трапеции её хозяйке.
M
K
A
D
H
( c м 2 )
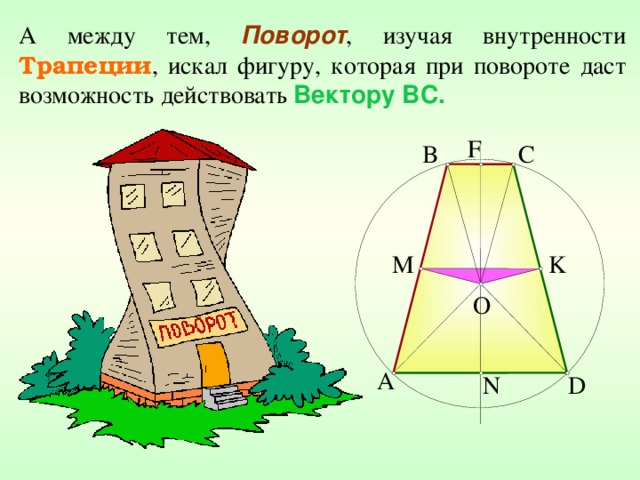
А между тем, Поворот , изучая внутренности Трапеции , искал фигуру, которая при повороте даст возможность действовать Вектору BC .
F
C
B
M
K
O
A
D
N
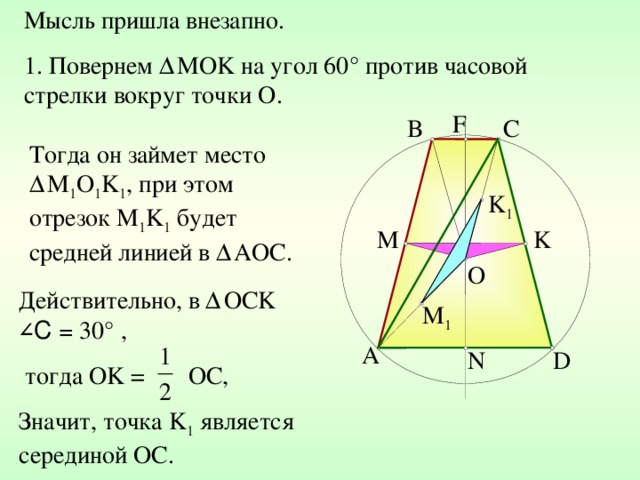
Мысль пришла внезапно.
1. Повернем Δ MOK на угол 60 ° против часовой стрелки вокруг точки О.
F
B
C
Тогда он займет место Δ M 1 O 1 K 1 , при этом отрезок M 1 K 1 будет средней линией в Δ AOC .
K 1
M
K
O
Действительно, в Δ ОС K ∠ С = 30 ° ,
тогда О K = ОС,
Значит, точка K 1 является серединой ОС.
M 1
A
D
N
Поворот
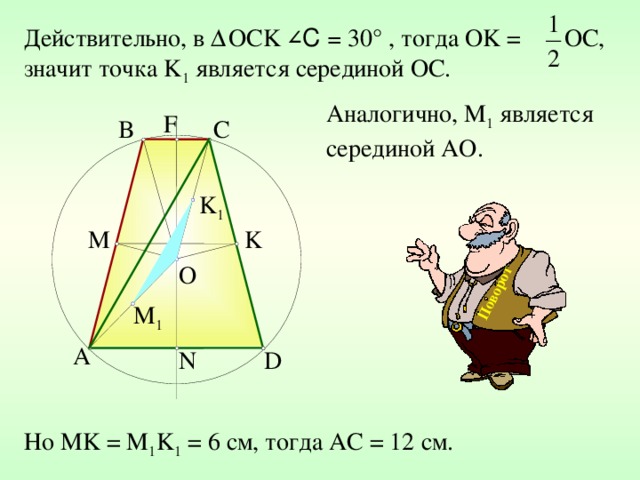
Действительно, в Δ ОС K ∠ С = 30 ° , тогда О K = ОС, значит точка K 1 является серединой ОС.
Аналогично, М 1 является серединой АО.
F
C
B
K 1
M
K
O
M 1
A
D
N
Но MK = M 1 K 1 = 6 см, тогда AC = 12 см.
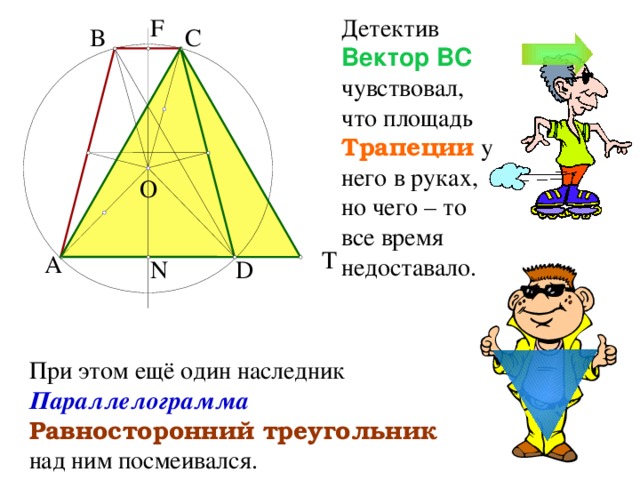
Детектив Вектор BC чувствовал, что площадь Трапеции у него в руках, но чего – то все время недоставало.
F
C
B
O
T
A
D
N
При этом ещё один наследник Параллелограмма Равносторонний треугольник над ним посмеивался.
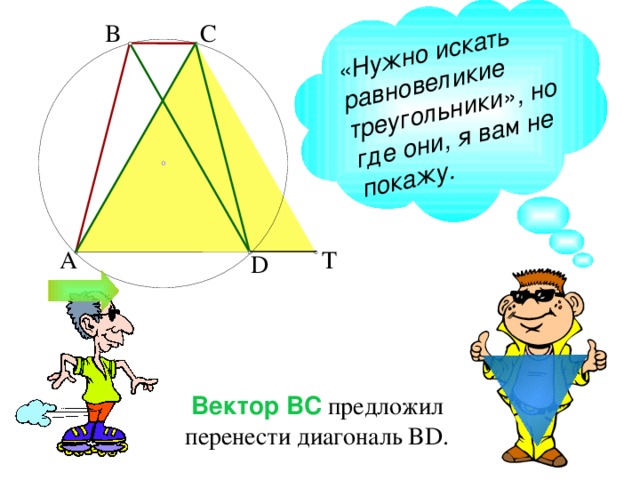
«Нужно искать равновеликие треугольники», но где они, я вам не покажу.
C
B
T
A
D
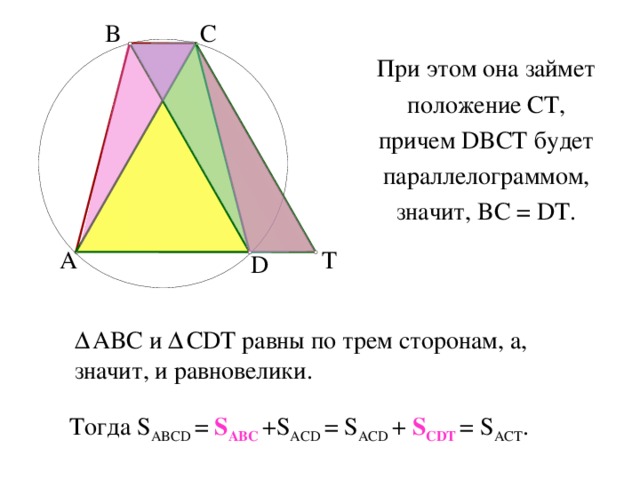
Вектор ВС предложил перенести диагональ BD .
B
C
При этом она займет положение CT , причем DBCT будет параллелограммом, значит, BC = DT.
A
T
D
Δ ABC и Δ CDT равны по трем сторонам, а, значит, и равновелики.
Тогда S ABCD = S ABC +S ACD = S ACD + S CDT = S ACT .
12
12
B
C
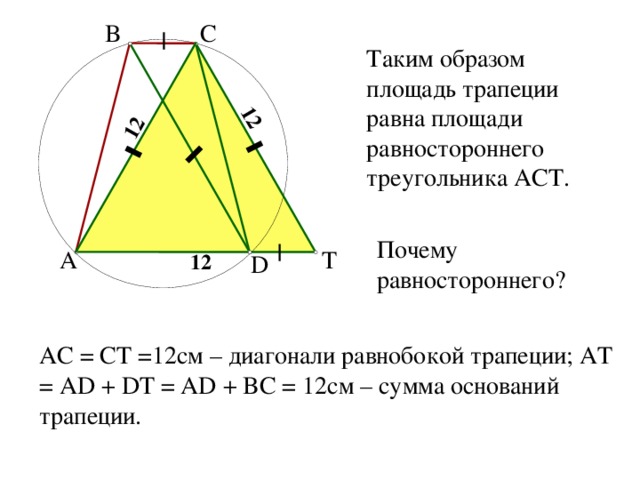
Таким образом площадь трапеции равна площади равностороннего треугольника ACT.
Почему равностороннего?
T
A
D
12
AC = CT =12 см – диагонали равнобокой трапеции ; AT = AD + DT = AD + BC = 12 см – сумма оснований трапеции.
C
B
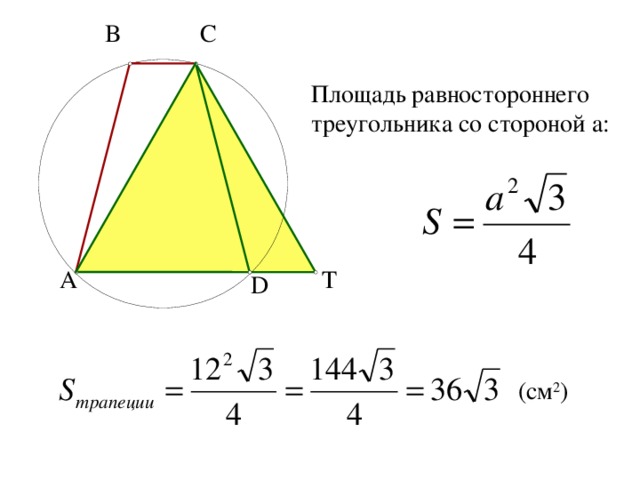
Площадь равностороннего треугольника со стороной a:
A
T
D
( c м 2 )

Ученики 9 «В» класса школы №1959 оказывают услуги жителям города Плоских фигур по отысканию площадей.
У нас просто смешные цены.
Каждая найденная площадь – пятерка по геометрии.
11 апреля 2003года Трапеция получила рекламное письмо.

Умникова А.
Щербакова Н.
Душанина Ю.
9 «В» класс
Руководитель
Козина Н.А.
Гомотетия

Трапеция счастлива. Наследство найдено.
Ученики школы №1959 могут открывать своё частное сыскное агентство. Их способ нахождения площадей Трапеции очень понравился.


 Получите свидетельство
Получите свидетельство Вход
Вход































































 Площадь трапеции (3.08 MB)
Площадь трапеции (3.08 MB)
 0
0 1065
1065 18
18 Нравится
0
Нравится
0



