Методическая разработка урока по геометрии "Площадь трапеции"

Цели (задачи) урока

образовательные: раскрыть содержание понятия «высота трапеции» на уровне способов действия; сформировать способы деятельности по решению задач на использование формулы площади трапеции через ее основание и высоту.

развивающие:

Развивать умение видеть проблему и выдвигать гипотезы по ее решению, развивать логическое мышление. Развивать умение работать в группах, математическую речь.

воспитательные: создать условия для воспитания коммуникативных навыков, воспитывать у учащихся любознательность.

Результаты урока

Предметные:

Знание учащимися определения «высота трапеции», умение строить высоту фигуры, обозначать ее на чертеже, выбирать отрезок, являющийся высотой с опорой на определение понятия «высота», умение записывать формулу площади, проговаривают ее, называют этапы вывода формулы (доказательство)

Метапредметные:

Формирование УУД: целеполагание планирование решения проблемы. Рефлексия, подведение под понятие, построение высказываний, обобщение, формулирование проблемы.

Личностные:

проявление любознательности и заинтересованности в изучении новой темы.

Тип урока, педагогическая технология

Изучение нового материала, технология проблемного диалога

Оборудование урока:

Учебник: Геометрия 7 - 9 кл. : учеб. для общеобразоват. учреждений / Атанасян и др. – М. : Мнемозина, 2010. , письменные принадлежности, компьютер с проектором, презентация к уроку, ролик «Физкультминутка»

Опорные понятия, термины:

Квадрат, прямоугольник, ромб, треугольник, площадь квадрата, площадь треугольника, площадь прямоугольника, площадь параллелограмма, высота треугольника и параллелограмма.

Ход урока

1. Организационный момент

Учитель начинает со слов приветствия:

Наш урок пора начать.

Пришло время вычислять.

И на трудные вопросы.

Вы ответ сумейте дать.

2.  Актуализация знаний. Постановка учебной проблемы

 Сегодня мы завершаем изучение площадей многоугольников. Учитель предлагает решить устно задачи по готовым чертежам на доске, среди которых есть задача на нахождении площади трапеции, в чем и возникает учебная проблема.

 - Решите те задачи, какие сможете:

 Площади каких многоугольников умеем находить?

Почему последнюю задачу не решили? (Мы не знаем, как находить площадь трапеции)

Итак, как вы думаете, какая тема сегодняшнего урока? Чему мы должны научиться? (Тема урока: Площадь трапеции. )

3. Поиск решения проблемы

Как мы находили площадь пятиугольника? (Складывали площади треугольников, на которые разбит пятиугольник)

 Что должно быть известно, чтобы мы могли найти площадь треугольника?

Весь материал – смотрите документ.

Конспект урока

Тема урока: Площадь трапеции.8 класс

Разработчик: Савченко Татьяна Александровна, учитель математики МБОУ СОШ №6 с углубленным изучением отдельных предметов

г. Ставрополя

Ход урока

1. Организационный момент

Учитель начинает со слов приветствия:

Наш урок пора начать.

Пришло время вычислять.

И на трудные вопросы.

Вы ответ сумейте дать.

Приветствует учащихся, отмечает отсутствующих, проверяет готовность к уроку.

1. Актуализация знаний. Постановка учебной проблемы

Сегодня мы завершаем изучение площадей многоугольников. Учитель предлагает решить устно задачи по готовым чертежам на доске, среди которых есть задача на нахождении площади трапеции, в чем и возникает учебная проблема.

- Решите те задачи, какие сможете:

Площади каких многоугольников умеем находить?

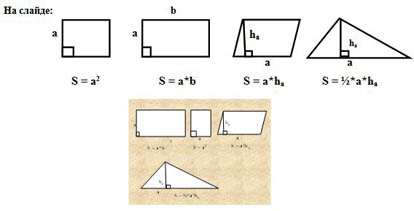
На слайде: b

h_a

h_a

а \\\ a

a

a

S = a² S = a*b S = a*h_a S = ½*a*h_a

Почему последнюю задачу не решили? (Мы не знаем, как находить площадь трапеции)

Итак, как вы думаете, какая тема сегодняшнего урока? Чему мы должны научиться? (Тема урока: Площадь трапеции.)

1. Поиск решения проблемы

Как мы находили площадь пятиугольника? (Складывали площади треугольников, на которые разбит пятиугольник)

Что должно быть известно, чтобы мы могли найти площадь треугольника? (на доске)

а) S=?

3

Пусть h=3, a=10. Нанесите на рисунок.

(1 человек у доски выполняет задание)

10

б) S=? Дано: S_1, S₂

S₂ Что должно быть известно, чтобы найти площадь

S₁ фигуры? Площади двух фигур?

Решите полученные задачи.

? Итак, мы нашли площадь неизвестного четырехугольника. Какие теоретические факты были использованы?

1. S_ф = сумме площадей фигур, их которых она состоит

2. S_Δ = ½*a*h

Вспомним, что такое трапеция? Как называются ее элементы?

! Подумаем, какие элементы трапеции надо знать, чтобы найти ее площадь?

1. Можно предположить: основание и высоту.

2. Постройте трапецию и выделите ее основания. Постройте отрезок, который по вашему мнению является высотой трапеции. (Ученики делают чертежи на доске и в тетрадях)

Постройте все высоты трапеции, сколько их?

На доске:

Определение Высота трапеции – это перпендикуляр, проведенный из любой точки одного основания на прямую, содержащую другое основание.

Длина высоты – расстояние между основаниями.

Задание на доске: Является ли высотой? Если нет, то постройте высоту.

1. 2. 3.

? ? ? ?

1. Итак, решим задачу:

Пусть будет известно: h=3, a=8, b=10.

• Постройте чертеж. Нанесите на него данные

• Сможем ли мы найти площадь трапеции?

• Есть ли подсказки на чертеже?

8

10

а) Надо разбить на два треугольника. б) Нужно провести диагональ

Вывод: Как удалось найти площадь трапеции, не зная ее формулы?

План: 1) Провели диагональ и разбили на два треугольника.

2) Нашли площадь каждого

3) Сложили площади

Слайд:

План решения задачи.

1. Разбить на два треугольника

2. S₁=? S₂=?

3. S_тр= S₁+S₂

? А если будут другие числа, то изменится ли ход решения задачи? Нет

Значит при любых значениях a,b и h мы, поступая так же, найдем площадь трапеции? Да

Решим задачу.

Дано: ABCD – трапеция

S, a, b, h

S_тр = (a+b)/2*h

B а C

A b D

Работаем по плану:

1. Разбиваем диагональю BD на ΔABD и ΔBDC

2. Найдем S_ΔABD = ½*a*h; S_BCD=1/2*b*h;

3. Найдем S_тр как сумму площадей S_тр=1/2*a*h+1/2*b*h=1/2*h*(a+b)

S_тр=1/2*(a+b)*h

Фронтальная работа с классом, один ученик у доски

Подведем итоги:

- Что нужно знать, чтобы найти площадь? (длины оснований и высоту)

-Сформулируйте теорему о том, что площадь трапеции равна (произведению полусуммы оснований на высоту). Прочитаем эту теорему в учебнике.

-Прочитайте формулу несколькими способами (площадь трапеции равна произведению полусуммы оснований на высоту; половина высоты умноженная на сумму оснований; произведение суммы оснований и высоты, деленная на два)

Вспомним еще раз каков план доказательства теоремы, что мы делали?

Динамическая пауза:

1. Формирование новых знаний и способов действий

? Какие элементы можно вычислить, зная площадь?

S=1/2*(a+b)*h

h=? h=2S/(a+b)

a=? a=2S/h-b

b=? b=2S/h-a

Решаем задачи по готовым чертежам.

1. Сформулируйте задачу по условию. Достаточно данных? Найдите S_тр=?

S=? 8

5

4

1. Сформулируйте задачу. Какое полезное свойство нужно учесть, чтобы решить задачу?

S=40 см²

12

?

28

Выполним самостоятельную работу. (индивидуальная работа по карточкам, самопроверка по слайду, самооценка)

№480, а.

1. АВ=21 см, СD=17см, высота BH=7см.

б, в решаем у доски (один ученик решает с комментированием)

Для учащихся с более высоким уровнем усвоения материала можно предложить

№481

Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135⁰.

1. Подведение итогов урока.

1. Что главное было на уроке?

2. С какой теоремой познакомились?

3. Каким способом решали задачи и доказали теорему?

Домашнее задание.

1. Высота и основания трапеции относятся как 5:6:4. Найдите меньшее основание трапеции, если S_тр=88см² , а высота меньше оснований.

2. Высота трапеции равна меньшему основанию и в 2 раза меньше большего основания. Найти высоту трапеции, если S_тр=54см²

3. Основания равнобедренной трапеции 12см и 16см, ее диагонали взаимно перпендикулярны. Найдите площадь трапеции.

Рефлексия: Обведите те высказывания, которые для вас являются истинными:

1. Данная тема мне понятна.

2. Я знаю, что такое высота трапеции и могу ее построить.

3. Я знаю, как найти площадь трапеции.

4. Я доволен своей работой на уроке.