Презентация по математике "Цилиндр"

Цель урока:

закрепить формулы площади поверхности цилиндра в практических заданиях.

Цилиндр — это тело, которое образуется при вращении прямоугольника вокруг прямой, содержащей его сторону.

Цилиндрические тела встречаются нам каждый день...

Формулы.

... площади боковой поверхности цилиндра:

=> Sбок. = 2πrh

... площади полной поверхности цилиндра:

=> Sполн. = Sбок. + 2Sосн. = 2πrh + 2πr² = 2πr(r+h)

h - высота цилиндра

r - радиус основания

Дифференцированные задания:

Вы — весёлый японский повар! 

Чтобы приготовить японское кушанье «роллы», надо из риса и морепродуктов сформировать цилиндры, а затем — обернуть их чёрной водорослью «нори», чтобы не развалились.

Задание №1.

Вычислить, какую площадь поверхности одного ролла надо обернуть водорослью «нори», если диаметр ролла 3 см, высота — 5 см. π ≈ 3, 14.

Цель урока :

закрепить формулы площади поверхности цилиндра в практических заданиях.

(Греция. Развалины храма Апполона)

Цель урока :

закрепить формулы площади поверхности цилиндра в практических заданиях.

(Барселона. Небоскрёб Agbar Tower)

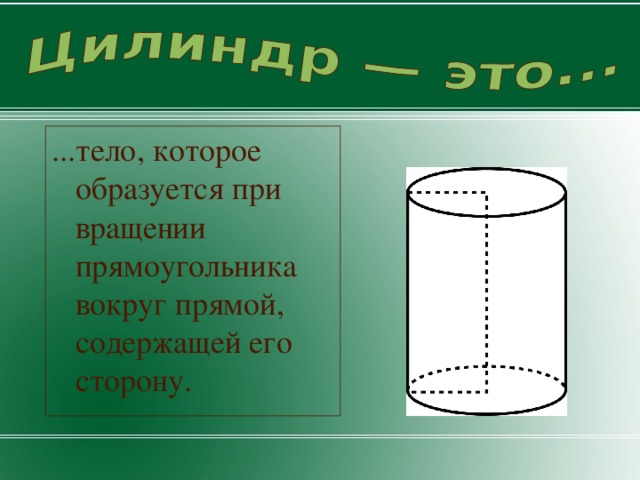
...тело, которое образуется при вращении прямоугольника вокруг прямой, содержащей его сторону.

...встречаются нам каждый день:

S бок. = 2 πr h ...площади полной поверхности цилиндра: = S полн. = S бок. + 2 S осн. = = 2 πrh + 2 πr 2 = 2 πr (r+h) h - высота цилиндра r - радиус основания " width="640"

...площади боковой поверхности цилиндра:

= S бок. = 2 πr h

...площади полной поверхности цилиндра:

= S полн. = S бок. + 2 S осн. =

= 2 πrh + 2 πr 2 = 2 πr (r+h)

h - высота цилиндра

r - радиус основания

Вы — весёлый японский повар!

Чтобы приготовить японское кушанье «роллы», надо из риса и морепродуктов сформировать цилиндры , а затем — обернуть их чёрной водорослью «нори», чтобы не развалились.

Вычислить, какую площадь поверхности одного ролла надо обернуть водорослью «нори», если диаметр ролла 3 см, высота — 5 см. π ≈ 3,14.

Задание №1.

Задание №2.

Сколько коробок водоросли «нори» надо приобрести весёлому повару, если он хочет приготовить 50 роллов диаметром 5 см и высотой 1,5 см. В одной коробке упаковано 10 см 2 водоросли «нори».

Вы — добрый мужественный сантехник!

Чтобы трубы (цилиндрической формы) не замерзали зимой, их обворачивают специальной плёнкой.

Задание №1.

Вычислить, какую площадь поверхности трубы надо обернуть плёнкой, если диаметр трубы 30 см, длина — 5 м. π ≈ 3,14.

Задание №2.

Вычислить, сколько рулонов плёнки понадобится доброму мужественному сантехнику, если он должен подготовить к зиме 150 труб длиной 10 м и диаметром 50 см. В одном рулоне - 5 0 м 2 плёнки. Результат округлить до целых в большую сторону.

Вы — гениальный учёный!

Чтобы Ваше Самое Главное Изобретение, наконец, заработало, главную деталь, имеющую форму цилиндра, надо покрыть жёлтой краской.

Задание №1.

Вычислить, какую площадь поверхности детали надо покрасить, если диаметр детали 5 см, длина — 15 см. π ≈ 3,14.

Л. В. Негодаева,

учитель математики

ЦДО г. Ростова-на-Дону

Права на использованные картинки и фотографии принадлежат их владельцам