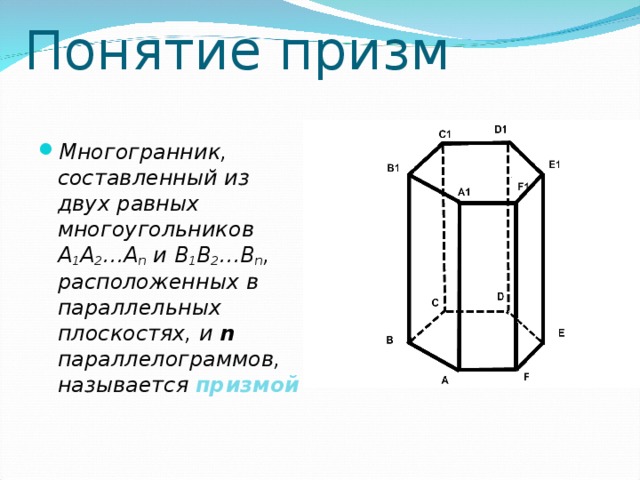
Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.

Элементы призмы
Основания – это грани, совмещаемые параллельным переносом.
Боковая грань – это грань, не являющаяся основанием.
Боковые рёбра – это отрезки, соединяющие соответствующие вершины оснований.
Вершины – это точки, являющиеся вершинами оснований.
Высота –это перпендикуляр, опущенный из одного основания на другое.
Диагональ -это отрезок, соединяющий две вершины, не лежащие в одной грани.

 Получите свидетельство
Получите свидетельство Вход
Вход







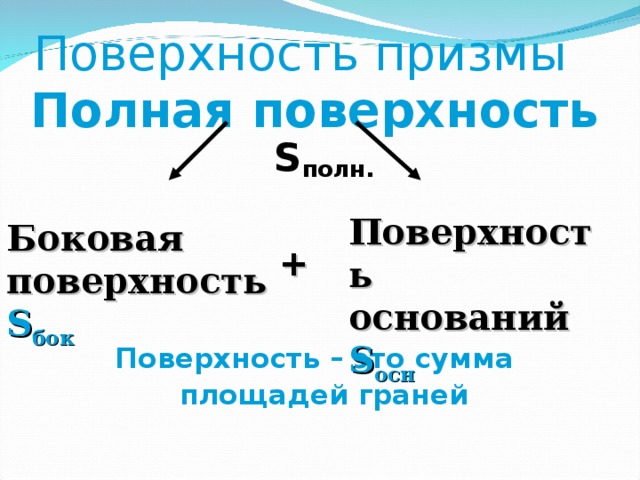


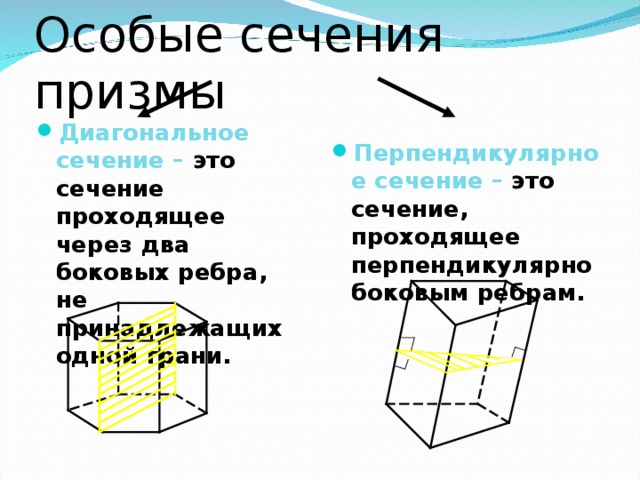










 Презентация по математике "Призма" (0.81 MB)
Презентация по математике "Призма" (0.81 MB)
 0
0 1128
1128 106
106 Нравится
0
Нравится
0





