Презентация по математике по теме "Равнобедренный треугольник, свойства равнобедренного треугольника"

Цель урока:

• ввести определение равнобедренного треугольника и его элементов;

• изучить свойства углов равнобедренного треугольника;

• научиться пользоваться доказанным свойством при решении задач.

Актуализация опорных знаний:

1.  Сформулируйте первый признак равенства треугольников?

(Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. )

Полную информацию смотрите в файле. 

Геометрия 7 класс

Тема урока:

Равнобедренный треугольник, свойства равнобедренного треугольника

Подготовила: учитель математики и информатики Матичева С.А.

Кольчугинская ОШ №1

Цель урока:

• ввести определение равнобедренного треугольника и его элементов;
• изучить свойства углов равнобедренного треугольника;
• научиться пользоваться доказанным свойством при решении задач.

• Сформулируйте первый признак равенства треугольников?

(Если две стороны и угол между ними одного

треугольника равны соответственно двум

сторонам и углу между ними другого

треугольника, то такие треугольники равны.)

Актуализация опорных знаний:

2. Какими могут быть треугольники в зависимости от величины углов? Дайте определение  каждого из них.

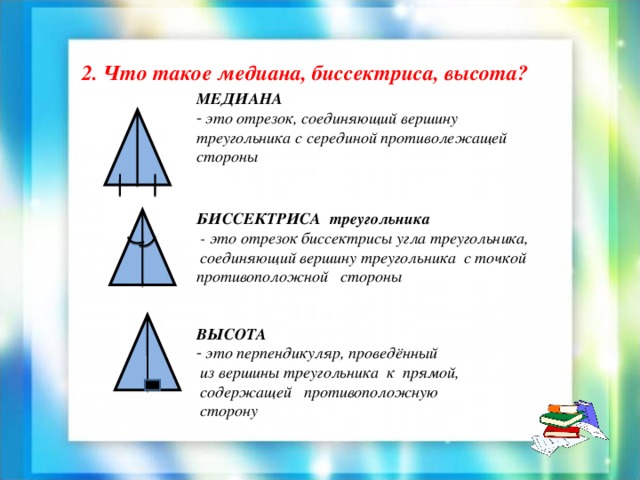
2. Что такое медиана, биссектриса, высота?

МЕДИАНА

• это отрезок, соединяющий вершину

треугольника с серединой противолежащей стороны

БИССЕКТРИСА треугольника

- это отрезок биссектрисы угла треугольника,

соединяющий вершину треугольника с точкой

противоположной стороны

ВЫСОТА

• это перпендикуляр, проведённый

из вершины треугольника к прямой,

содержащей противоположную

сторону

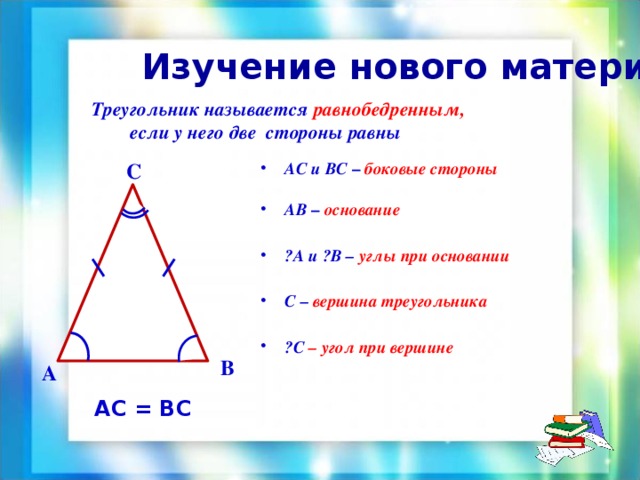
Изучение нового материала:

Треугольник называется равнобедренным,

если у него две стороны равны

C

• АС и ВС – боковые стороны

• АВ – основание

• ے А и ے В – углы при основании

• С – вершина треугольника

• ے С – угол при вершине

B

A

АС = ВС

В равнобедренном треугольнике

А BC А B = BC . Назовите основание и

углы при основании этого

треугольника. ( AC , ے A , ے C )

Дан равнобедренный треугольник

MKN c основанием MN . Назовите

боковые стороны и углы при

основании этого треугольника.

( MK и KN , ے M , ے N )

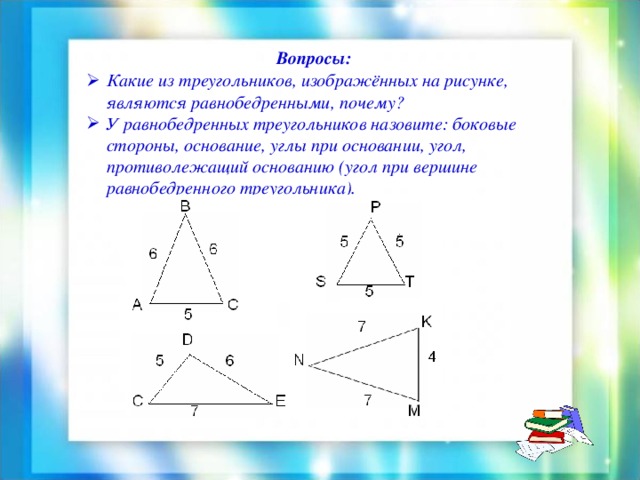
Вопросы:

• Какие из треугольников, изображённых на рисунке, являются равнобедренными, почему? У равнобедренных треугольников назовите: боковые стороны, основание, углы при основании, угол, противолежащий основанию (угол при вершине равнобедренного треугольника).
• Какие из треугольников, изображённых на рисунке, являются равнобедренными, почему?
• У равнобедренных треугольников назовите: боковые стороны, основание, углы при основании, угол, противолежащий основанию (угол при вершине равнобедренного треугольника).

Теорема . В равнобедренном треугольнике

углы при основании равны .

Дано: ∆ ABC , CA = CB .

Доказать : в ∆ ABC ے A = ے B .

Доказательство.

∆ CAB = ∆ CBA по двум сторонам

и углу между ними. Действительно,

у них CA = CB, CB = CA по условию,

угол при вершине С – общий.

Из равенства треугольников

следует равенство соответствующих

углов, т. е. ے А = ے В.

Теорема доказана.

C

B

A

Закрепление нового материала:

• В равнобедренном треугольнике боковая сторона равна 10см, а основание 5см. Вычислите периметр треугольника.

• В равнобедренном треугольнике основание равно 8см, а периметр равен 24см. Вычислите боковую сторону треугольника.

• В равнобедренном треугольнике боковая сторона равна 10см, а периметр 20см. Вычислите основание треугольника.

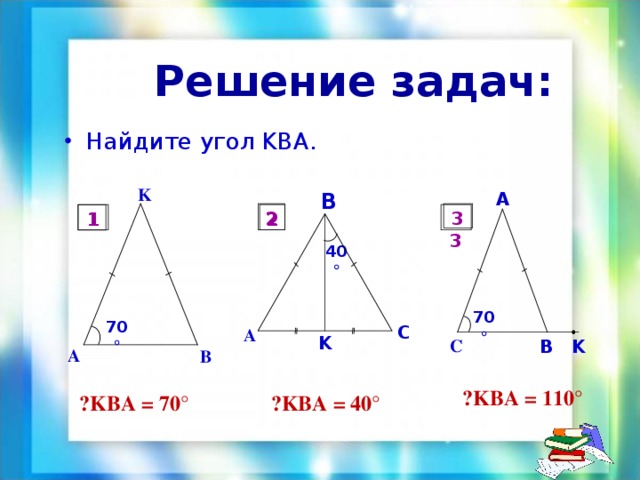
Решение задач:

• Найдите угол KBA .

K

A

B

2

3

1

3

2

1

40 

70 

70 

C

A

K

C

B

K

A

B

ے KBA = 110°

ے KBA = 40°

ے KBA = 70°

Подведение итогов урока:

Вопросы к учителю?

Выставление оценок:

Домашнее задание :

1. Найти угол КВА. (задания – на карточке).

A

K

A

C

3

B

1

22

B

B

50 

A

70 

K

C

E

K

2. Читать: глава 2, параграф 2, пункт 18

Спасибо за внимание!