Целью данного урока является:познакомить детей с методом нахождения корней квадратного уравнения путем выделения квадрата двучлена.
Повторить определение квадратного уравнения, вспомнить приемы решения неполных квадратных уравнений; формулы сокращенного умножения.
Задачи урока:
научить детей находить корни квадратного уравнения, выделением квадрата двучлена;
закрепить умения решать неполные квадратные уравнения;
самостоятельно находить пути решения поставленной задачи;
уметь объективно оценивать свои знания. Презентация лаконична , проста и понятна детямдаже для самостоятельного использования при обучении на дому.

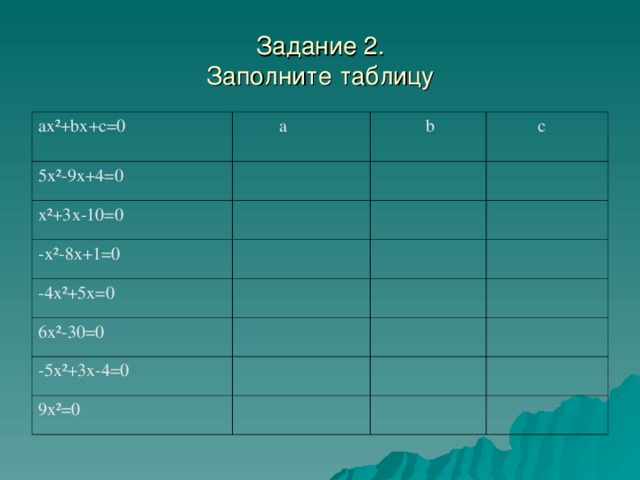
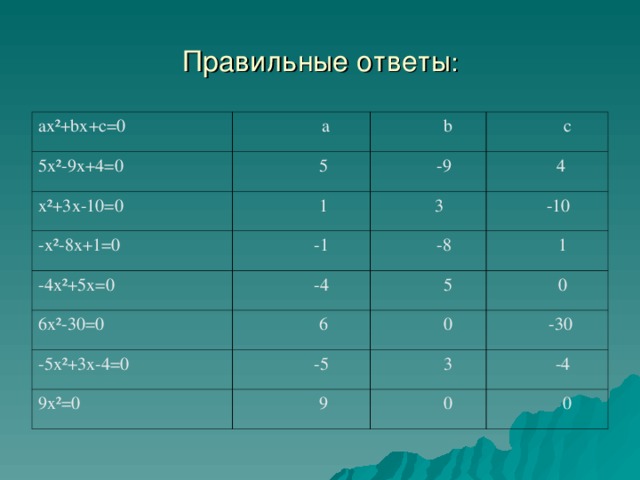
Общий вид квадратного уравнения.
ах²+bx+c=0,
а, b, с – некоторые числа, а≠0.
Неполные квадратные уравнения:
ах²=0, когда b=0, с=0.
ах²+ bх=0, когда с=0.
Приведённые квадратные уравнения:
Х²+px+g=0, когда а=1.

 Получите свидетельство
Получите свидетельство Вход
Вход






























 Презентация по математике "Нахождение корней квадратного уравнения выделением квадрата двучлена" (0.45 MB)
Презентация по математике "Нахождение корней квадратного уравнения выделением квадрата двучлена" (0.45 MB)
 0
0 905
905 111
111 Нравится
0
Нравится
0


