Презентация по математике на тему "Тестовые задания по геометрии"

1. Задачи на треугольник.

При решении вычислительных задач на треугольник нужно знать следующие формулы:

S=1/2*ah_a=1/2absinƔ=(p(p-a) (p-b) (p-c))^1/2=pr=abc/4R;

R=a/2sina=abc/4S;

r=S/p;

1/h_a+1/h_b+1/h_c=1/r;

a²=b²+c²-2bccosa;

a/sina=b/sinß=c/sinƔ=2R

m_a=(2(b²+c²) -a²)^1/2/2;

l_a=(bc(b+c+a) (b+c-a))^1/2/b+c.

Биссектриса треугольника обладает одним замечательным свойством: она делит противолежащую сторону на отрезки, пропорциональные соответствующим боковым сторонам

Иногда применяют формулу расстояния между центрами описанной и вписанной окружности

d=(R²-2rR)^1/2.

Задача №1.

Найдите площадь треугольника со сторонами

2, 3, √5

Решение: Задачу можно решить по формуле Герона

S=(p(p-a) (p-b) (p-c))^1/2

Проще решить задачу можно было бы так. По теореме косинусов:

(√5) 2=3²+2²-2*3*3*cosa (см. рис). 5=13-12cosa, cosa=8/12=2/3.

ТЕСТОВЫЕ

ЗАДАНИЯ ПО

ГЕОМЕТРИИ

НА ЕНТ

Уральск, 2015

. I. Задачи на треугольник

При решении вычислительных задач на треугольник нужно знать следующие формулы

Биссектриса треугольника обладает одним замечательным свойством: она делит противолежащую сторону на отрезки, пропорциональные соответствующим боковым сторонам

Иногда применяют формулу расстояния между центрами описанной и

вписанной окружности

с

h

в

α

  Задача №1

Найдите площадь треугольника со сторонами

2,3,√5

Решение : Задачу можно решить по

формуле Герона

Проще решить задачу можно было бы так. По теореме косинусов:

Так как площадь треугольника равна половине произведения двух сторон на синус угла между ними, то:

О ответ:

Задача №2

Длины сторон а, b, с треугольника равны 2, 3 и 4. Найти расстояние между центрами описанной и вписанной окружностей.

Решение. Для решения задачи даже чертеж не нужен. Последовательно находим по формулам полупериметр, площадь, радиусы описанной и вписанной окружности , расстояние между центрами описанной и вписанной окружностей.

Задача 3 .  Основание равнобедренного треугольника равно 4√2, медиана боковой стороны равна 5. Найдите длину боковой стороны

Решение: Можно воспользоваться готовой формулой длины медианы. Обозначим АВ через 2х, тогда ВМ = МС =х .

Имеем:

АВ = ВС = 6. Задачу можно решить по-другому. Из ∆ABC по теореме косинусов:

Далее, по той же теореме косинусов из ∆АМВ:

Ответ: 6.

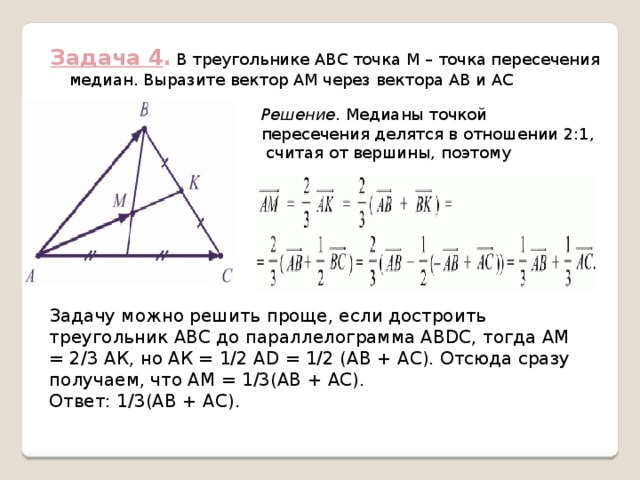
Задача 4 .  В треугольнике ABC точка М – точка пересечения медиан. Выразите вектор AM через вектора АВ и АС

Решение . Медианы точкой пересечения делятся в отношении 2:1,

считая от вершины, поэтому

Задачу можно решить проще, если достроить треугольник ABC до параллелограмма ABDC, тогда AM = 2/3 АК, но АК = 1/2 AD = 1/2 (АВ + АС). Отсюда сразу получаем, что AM = 1/3(АВ + АС).

Ответ: 1/3(АВ + АС).

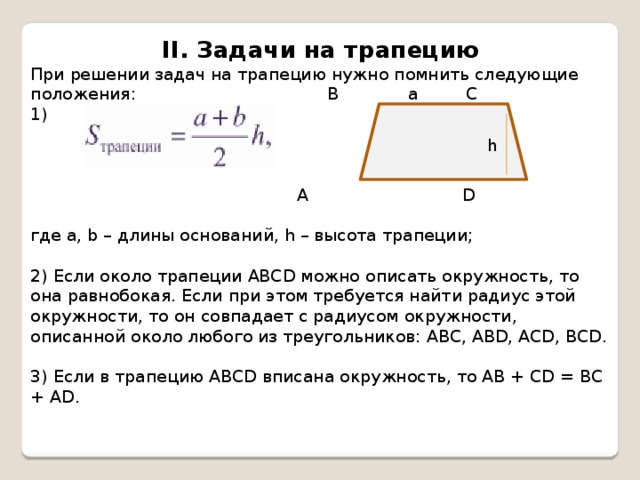
II. Задачи на трапецию

При решении задач на трапецию нужно помнить следующие положения: B a C

1)

A D

где а, b – длины оснований, h – высота трапеции;

2) Если около трапеции ABCD можно описать окружность, то она равнобокая. Если при этом требуется найти радиус этой окружности, то он совпадает с радиусом окружности, описанной около любого из треугольников: ABC, ABD, ACD, BCD.

3) Если в трапецию ABCD вписана окружность, то AB + CD = BC + AD.

h

Ответ: 5; 15

Задача5 Средняя линия трапеции равна 10 и делит площадь трапеции в отношении 3:5. Найдите длины оснований этой трапеции

Решение. Рассмотрим трапеции EBCF и AEFD (рис. ). Введем обозначения: AD = х, ВС = у; высоты трапеций EBCF и AEFD обозначим через h. Так как площадь трапеции равна произведению полусуммы оснований на высоту трапеции, то

Ответ

Из свойства средней линии трапеции:

Таким образом, получаем систему уравнений :

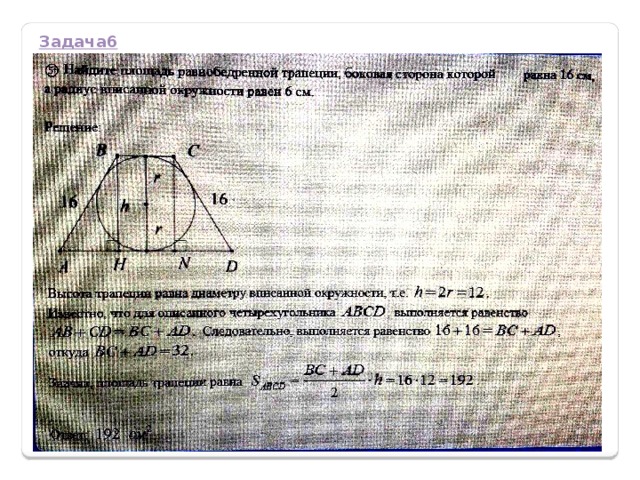
Задача6

Для произвольного выпуклого четырёхугольника

S = ½ d 1 d 2 sinα. Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны, a S = рr, где р – полупериметр, r – радиус вписанной окружности.

Если около четырёхугольника можно описать окружность, то суммы противоположных углов равны по 180°.

Для правильного n-угольника:

III. Задачи на параллелограмм ( выпуклые четырехугольники)

Площадь параллелограмма со сторонами а, b и углом α между ними вычисляется по формуле S = absinα. Можно также воспользоваться формулой S = ½ d 1 d 2 sinα где d 1 , d 2 – длины диагоналей, α – угол между ними (или S = ah a , где h a – высота). Если в параллелограмм можно вписать окружность, то это ромб. Если около параллелограмма можно описать окружность, то это прямоугольник.

R и r – радиусы описанной и вписанной окружностей, а – длина стороны правильного n-угольника).

Полезно также помнить, что в правильном шестиугольнике a6 = R.

3√ a

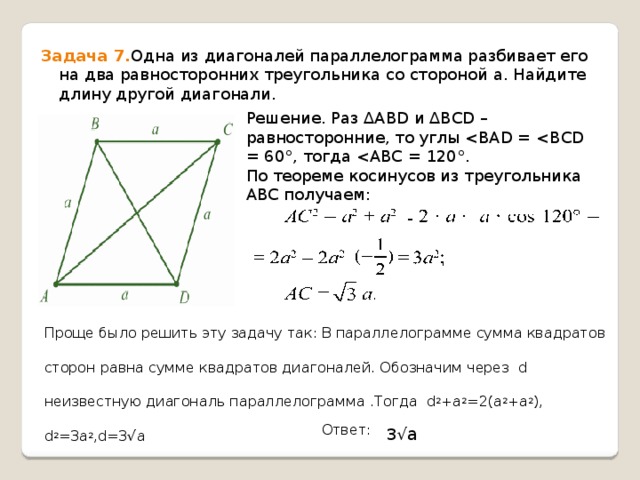
Задача 7. Одна из диагоналей параллелограмма разбивает его на два равносторонних треугольника со стороной а. Найдите длину другой диагонали.

Решение. Раз ∆ABD и ∆BCD – равносторонние, то углы

По теореме косинусов из треугольника ABC получаем:

-

Проще было решить эту задачу так: В параллелограмме сумма квадратов сторон равна сумме квадратов диагоналей. Обозначим через d неизвестную диагональ параллелограмма .Тогда d 2 +а 2 =2(а 2 +а 2 ), d 2 =3а 2 ,d=3√a

Ответ:

Задача 8 .  Высота ромба равна 12, а одна из его диагоналей равна 15. Найдите площадь ромба

Решение. Для нахождения площади ромба нам нужно знать длину стороны ромба и хотя бы один из его углов. Пусть АВ = α;

Делим первое уравнение на второе :

Ответ: 150 .

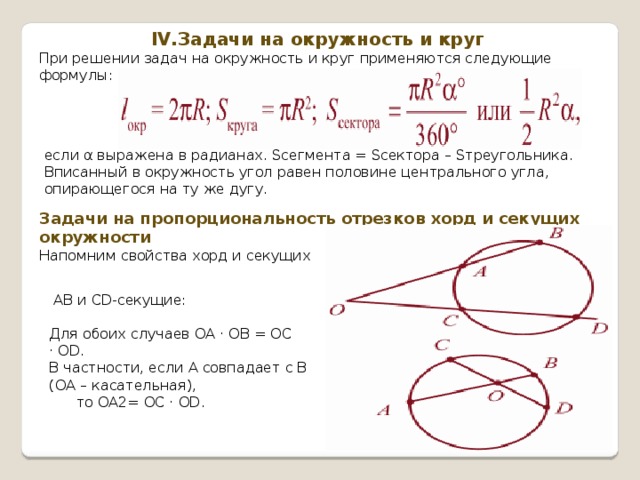
IV.Задачи на окружность и круг

При решении задач на окружность и круг применяются следующие формулы:

если α выражена в радианах. Sсегмента = Sсектора – Sтреугольника.

Вписанный в окружность угол равен половине центрального угла, опирающегося на ту же дугу.

Задачи на пропорциональность отрезков хорд и секущих окружности

Напомним свойства хорд и секущих

AB и СD-секущие:

Для обоих случаев ОА · ОВ = ОС · OD.

В частности, если А совпадает с В (ОА – касательная),

то ОА2= ОС · OD .

Таким образом

С учётом условия получаем уравнение

Задача9. Сторона квадрата, вписанного в окружность, отсекает сегмент, площадь которого (2п – 4) см 2 . Найдите периметр квадрата .

Решение. Площадь заштрихованного сегмента,

как видно из рисунка, можно вычислить по формуле :

где α – длина стороны квадрата, R – радиус описанной окружности. Выразим R через α.

Р квадрата = 4a = 4·4 = 16 см.

Ответ: 16 см.

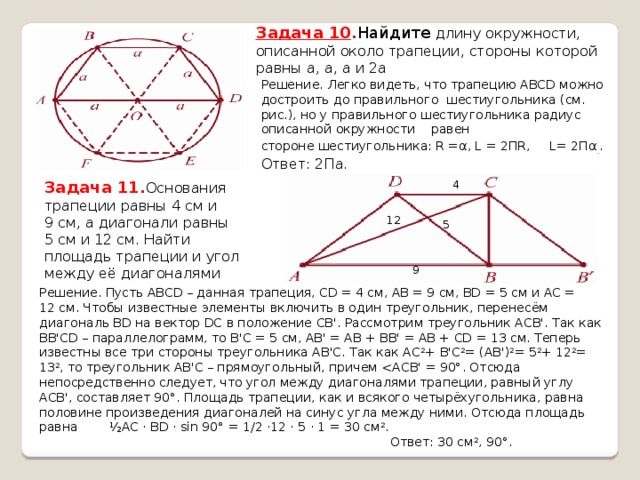
Задача 10 . Найдите длину окружности, описанной около трапеции, стороны которой равны а, а, а и 2а

Решение. Легко видеть, что трапецию ABCD можно достроить до правильного шестиугольника (см. рис.), но у правильного шестиугольника радиус описанной окружности равен

стороне шестиугольника: R =α, L = 2ΠR, L= 2Πα . . Ответ: 2Πа.

Задача 11 . Основания трапеции равны 4 см и 9 см, а диагонали равны 5 см и 12 см. Найти площадь трапеции и угол между её диагоналями

4

12

5

9

Решение. Пусть ABCD – данная трапеция, CD = 4 см, АВ = 9 см, BD = 5 см и АС = 12 см. Чтобы известные элементы включить в один треугольник, перенесём диагональ BD на вектор DC в положение СВ'. Рассмотрим треугольник АСВ'. Так как ВВ'CD – параллелограмм, то В'С = 5 см, АВ' = АВ + ВВ' = АВ + CD = 13 см. Теперь известны все три стороны треугольника АВ'С. Так как АС 2 + В'С 2 = (АВ') 2 = 5 2 + 12 2 = 13 2 , то треугольник АВ'С – прямоугольный, причем

Ответ: 30 см 2 , 90°.

Задача12. Дано: ОА = 4, АВ = 3, CD = 2 . Найдите ОС .

Решение. Пусть ОС = х, тогда ОА·ОВ =ОС·OD;

4 · 7 = х ( х + 2);

Ответ :

Задача 13 .Стороны прямоугольника равны α и b

На стороне α, как на диаметре, построена окружность.

На какие отрезки окружность делит диагональ прямоугольника

Решение. Из точки С проведена секущая СА и касательная CD к окружности. По известному свойству имеем: СР · СА = CD 2 ;

Ответ :

V. ЗАДАЧИ по СТЕРЕОМЕТРИИ

.

.

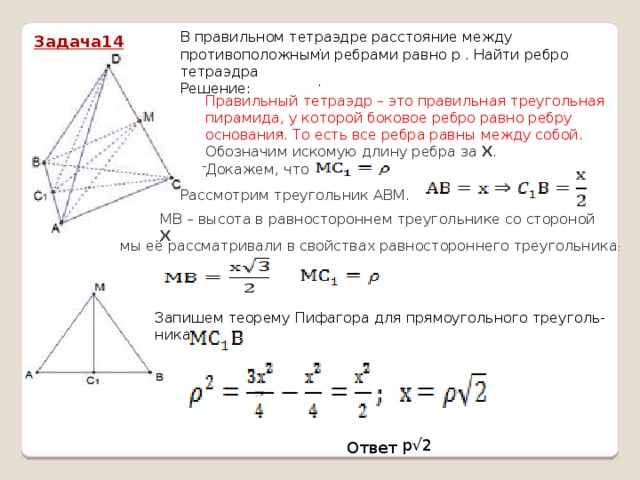
В правильном тетраэдре расстояние между противоположными ребрами равно р . Найти ребро тетраэдра

Решение:

Задача14

.

.

Правильный тетраэдр – это правильная треугольная пирамида, у которой боковое ребро равно ребру основания. То есть все ребра равны между собой. Обозначим искомую длину ребра за  Х .

Докажем, что

  .

 –

Рассмотрим треугольник АВМ.

МВ – высота в равностороннем треугольнике со стороной Х  

a

мы её рассматривали в свойствах равностороннего треугольника :

Запишем теорему Пифагора для прямоугольного треуголь-

ника 

р√2

Ответ

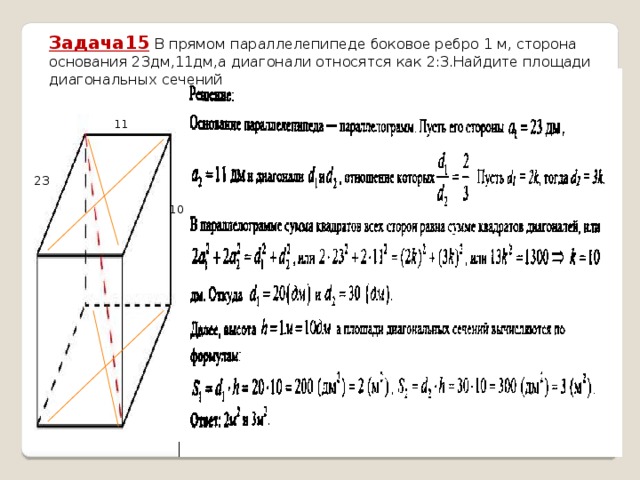
Задача15 В прямом параллелепипеде боковое ребро 1 м, сторона основания 23дм,11дм,а диагонали относятся как 2:3.Найдите площади диагональных сечений

11

23

10

Задача16

• Спасибо за внимание .Удачи всем на ЕНТ !
• Спасибо за внимание .Удачи всем на ЕНТ !
• Спасибо за внимание .Удачи всем на ЕНТ !

УДАЧИ НА ЕНТ !!!