
Алгебра – 7

Содержание:
- Прямоугольная система координат на плоскости.
- Построение точек по данным координатам.
- Функция. Историческая справка.
- Понятие функции.
- Способы создания функции.
- Функция y=kx .
- Линейная функция и ее график.
- Проверочный тест.

Устный опрос:
1. Что значит задать прямоугольную систему координат на плоскости?
2. Как построить точку, зная ее координаты?
3. Что такое функция?
4. Сколько способов задания функции вы знаете?
5. Что такое график функции?
6. Какая функция называется линейной?
7. Что является графиком линейной функции?
8. Сколько нужно точек, что бы построить прямую?
9.Как получить график функции у = k х - b ?

х
1
а) у = х + 5 б) у = + 2 в) у = 3;
г) у = - 3 х – 1; к) у = 3 х – 1; л) у = + 3;
м) у = 3 х.
4
2
2
х
- Найти функцию, которая не является линейной.
- График какой из функций изображен на рисунке?
3. Через какую из точек М (-1;0), А(0;0), D (0;2), С(2; 0) проходит график функции б)?
4. Указать функцию, график которой параллелен графику
функции у = х ?
Л
К
Д
А
1
2
Дана линейная функция у = ½ х – 2. Определите, какая их точек А(1, -1), В(-8, -6), Д(-8,-6), К(-4,4) принадлежит графику данной функции и лежит в одной координатной четверти с точкой М (-20,-25)
2
3
«Клад – это ваши знания».
В одной и той же системе координат построить графики функций у = 3 х + 5 и у = 2 х – 5. Найти точку пересечения полученных графиков.
1
Для функции у = - 4х+8 найдите:
а) значение х, при котором у=-2;
б) чему равно значение у при х = 1.

Тест
- Функция задана формулой у = 2х – 15. Определите:
а) значение у , если х = -3,5;
А. -8. Б. -22. В. 22.
б) значение х, при котором у = -3;
А. 6. Б. -6. В. -21.
- Найдите значение с, если известно, что график функции у = 3х + с проходит через точку А (5; 9).
А. 6. Б. -6. В. -22.
3) Задайте формулой линейную функцию, график которой параллелен прямой у = 4х+7 и проходит через начало координат.
А. у = 4х. Б. у = - 4х. В. У = 7х + 4.
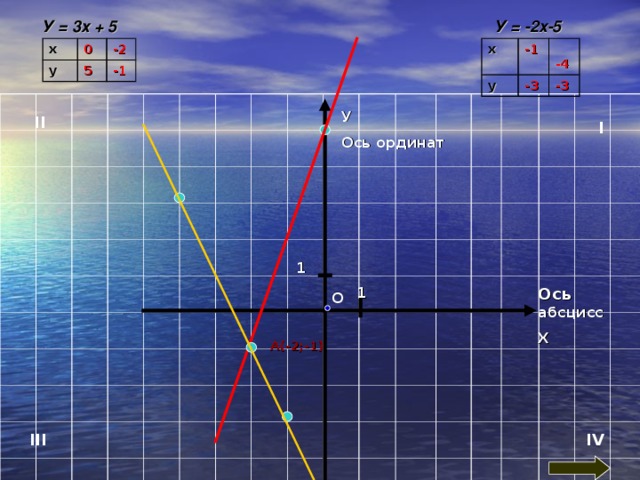
У = 3х + 5
У = -2х-5
х
х
0
у
-1
у
5
-3
-4
-2
-1
-3
У
Ось ординат
II
I
1
1
Ось абсцисс
Х
О
А(-2;-1)
IV
III

Дана линейная функция у = ½ х – 2. Определите, какая их точек А(1, -1), В(-8, -6), Д(-8,-6), К(-4,4) принадлежит графику данной функции и лежит в одной координатной четверти с точкой М (-20,-25)
Решение:
2) В(-2; -1) –
-1=1/2 * (-2) – 2;
-1=-3
не принадлежит
не принадлежит
-1=1/2 * (-1) – 2;
-1=-2 1/2
3) Д(-8; -6) –
-6=1/2 * (-8) – 2;
-6=-6
4) К(-4; 4) –
4 =1/2 * (-4) – 2;
4=-4
принадлежит
не принадлежит
М (-20,-25)
- III четверть
В(-2; -1) и Д(-8; -6)

Для функции у = - 4х+8 найдите:
а) значение х, при котором у = - 2;
б) чему равно значение у при х = 1.
у = - 4х+8
а) у = - 2.
-2 = - 4х+8;
4х = 8 +2;
4х = 10;
х = 2,5
у = - 4х+8
б) х = 1.
у = - 4*1+8;
у = - 4 +8;
у = 4.
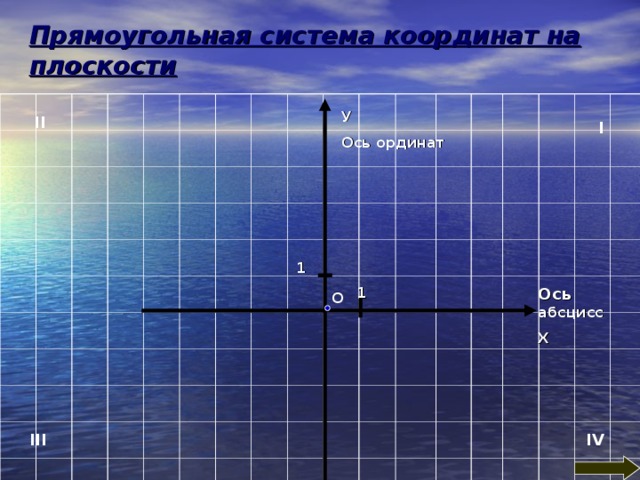
Прямоугольная система координат на плоскости
У
Ось ординат
II
I
1
Ось абсцисс
Х
1
О
III
IV
абсцисса
ордината
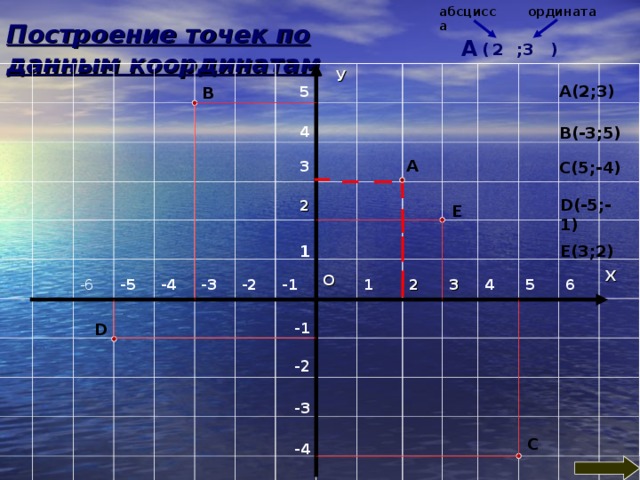
Построение точек по данным координатам
А
2
( ; )
3
У
А(2;3)
5
В
4
В(-3;5)
А
3
С(5;-4)
D(-5 ; -1)
2
Е
1
Е(3;2)
Х
О
3
2
6
4
5
-1
-2
-3
-4
-5
-6
1
-1
D
-2
-3
С
-4

Функция. Историческая справка
«Слово функция появилось в математике сравнительно недавно. Впервые о функции стал говорить великий немецкий математик и философ Готфрид Вильгельм Лейбниц в конце XVII века»
Г.В.Лейбниц
Леонард Эйлер (1707-1783 гг.), крупнейший математик XVIII столетия, в своей книге «Введение в анализ» формулировал определение функции так:
«Функция переменного количества есть аналитическое выражение, составленное каким-либо способом из этого переменного количества или постоянного количества»

Понятие функции
«Зависимость одной переменной от другой, при которой каждому значению независимой переменной соответствует значение зависимой переменной, называют функциональной зависимостью или функцией»
Задача : Поезд движется из Москвы в Санкт-Петербург со скоростью 120 км/ч. Какой путь пройдет поезд за t часов?
S – искомый путь в километрах
переменные
t - время в часах
S = 120 t
зависимая переменная
независимая переменная
2
3
S= a
b=2n+1
y = -3 х+4
V =a
Р=4а
У(х)=7х-21
S (t) = 60 t
x(y) = -3y+5
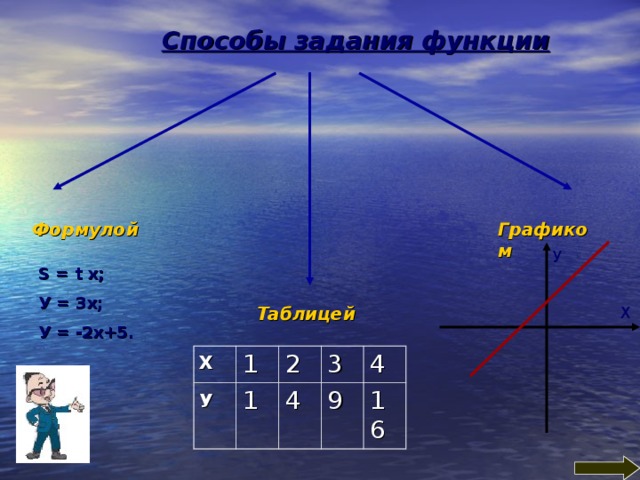
Способы задания функции
Формулой
Графиком
У
S = t x ;
У = 3х;
У = -2х+5.
Таблицей
Х
1
1
2
3
4
9
4
16
Х
У

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям независимой переменной, а ординаты – соответствующим значениям функции.
у
у
М
х
х

Линейной функцией называется функция вида у = k х + b , где k и b – заданные числа
Графиком линейной функции у = k х + b является прямая
у = k х
у
у = k х -3
х
0
-3
График функции у = k х + b получается сдвигом графика функции у = k х на b единиц вдоль оси ординат. Графиками функций у = k х и у = k х + b являются параллельные прямые.
Для построения прямой достаточно двух точек.


 Получите свидетельство
Получите свидетельство Вход
Вход




























 Презентация по математике "Линейная функция" (0.91 MB)
Презентация по математике "Линейная функция" (0.91 MB)
 0
0 483
483 73
73 Нравится
0
Нравится
0


