Презентация по информатике "Системы счисления"

Система счисления - это способ записи чисел с помощью заданного набора специальных знаков (цифр).

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число.

Любая позиционная система характеризуется своим основанием.

 Основание позиционной системы счисления - это количество различных знаков или символов, используемых для изображения цифр в данной системе.

Наиболее употребляемыми в настоящее время позиционными системами являются:

2 — двоичная (используется в программировании, информатике);

8 — восьмеричная;

10 — десятичная (используется повсеместно);

12 — двенадцатеричная (счёт дюжинами);

16 — шестнадцатеричная (используется в программировании, информатике);

60 — шестидесятеричная (единицы измерения времени, измерение углов и координат долготы и широты).

Системы счисления.

Ли Олег Енсуевич учитель информатики МБОУ Гимназия №3 г. Южно-Сахалинск.

Система счисления - это способ записи чисел с помощью заданного набора специальных знаков (цифр).

Системы счисления

Позиционные

Непозиционные

Смешанные

Позиционные системы счисления.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число.

Любая позиционная система характеризуется своим основанием .

Основание позиционной системы счисления - это количество различных знаков или символов, используемых для изображения цифр в данной системе.

Позиционные системы счисления.

Наиболее употребляемыми в настоящее время позиционными системами являются:

2 — двоичная (используется в программировании, информатике);

8 — восьмеричная;

10 — десятичная (используется повсеместно);

12 — двенадцатеричная (счёт дюжинами);

16 — шестнадцатеричная (используется в программировании, информатике);

60 — шестидесятеричная (единицы измерения времени, измерение углов и координат долготы и широты).

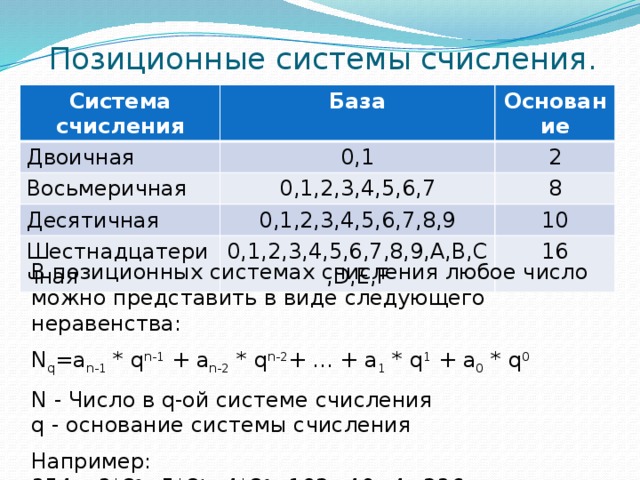
Позиционные системы счисления.

Система счисления

База

Двоичная

Восьмеричная

Основание

0,1

Десятичная

0,1,2,3,4,5,6,7

2

Шестнадцатеричная

0,1,2,3,4,5,6,7,8,9

8

0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

10

16

В позиционных системах счисления любое число можно представить в виде следующего неравенства:

N q =a n-1 * q n-1 + a n-2 * q n-2 + ... + a 1 * q 1 + a 0 * q 0

N - Число в q-ой системе счисления

q - основание системы счисления

Например: 354 8 =3*8 2 +5*8 1 +4*8 0 =192+40+4=236 10

Позиционные системы счисления.

Древнекитайская десятеричная

-548

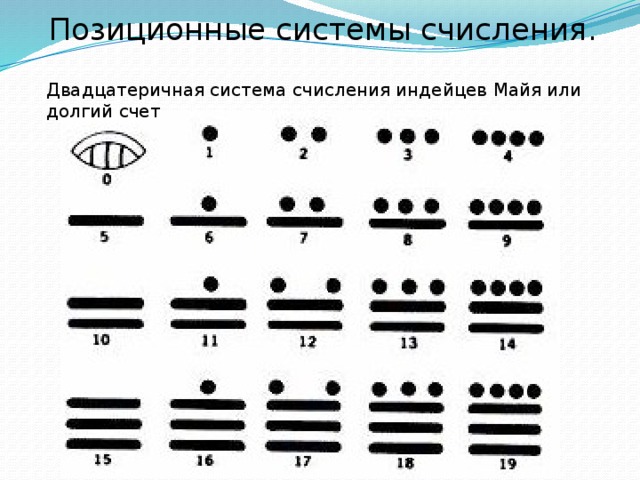
Позиционные системы счисления.

Двадцатеричная система счисления индейцев Майя или долгий счет

Непозиционные системы счисления.

Древнеегипетская десятичная

Римская пятеричная

Непозиционные системы счисления.

Славянская глаголическая

десятеричная

Славянская кириллическая

десятеричная алфавитная

Непозиционные системы счисления.

Недостатки непозиционной системы счисления

Непозиционные системы счисления имеют ряд существенных недостатков:

1. Существует постоянная потребность введения новых знаков для записи больших чисел.

2. Невозможно представлять дробные и отрицательные числа.

3. Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения. В частности, у всех народов наряду с системами счисления были способы пальцевого счета, а у греков был счетная доска абак – что-то наподобие наших счетов.

Непозиционные системы счисления.

Но мы до сих пор пользуемся элементами непозиционной системы счисления в обыденной речи, в частности, мы говорим сто, а не десять десятков, тысяча, миллион, миллиард, триллион.

Смешанные системы счисления

Наиболее известным примером смешанной системы счисления является представление времени в виде количества суток, часов, минут и секунд. При этом величина « d - дней, h - часов, m - минут, s - секунд» соответствует значению d • 24 • 60 • 60+h • 60 • 60+m • 60+s секунд.