Презентация по информатике на тему "Системы счисления"

Система счисления – это запись чисел по определённым правилам с помощью цифр.

В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.

Непозиционной системой счисления называется система, в которой вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа.

Позиционной системой счисления называется система, в которой вес каждой цифры измеряется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.

Римская система является современной непозиционной системой счисления. До сих пор римские числа очень часто используются.

В ней для записи различных целых чисел используются символы I, V, X, L, C, D, M и т.д., обозначающие соответственно 1, 5, 10, 50,100,500,1000 и т.д.

Если слева от старшей цифры стоит младшая, то она отнимается. Если младшая цифра стоит справа от старшей, то она прибавляется.

XXVIII=10+10+5+1+1+1=28

MCMLXXXV = запишите самостоятельно

Полную информацию смотрите в файле.

Муниципальное бюджетное

общеобразовательное учреждение

«Средняя общеобразовательная школа №12»

город Байкальск

Слюдянского района Иркутской области

Системы счисления

Семенько Татьяна Владимировна,

преподаватель информатики

• Система счисления –

это запись чисел по определённым правилам с помощью цифр.

• В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.

Существуют позиционные и непозиционные системы счисления.

• Непозиционной системой счисления называется система, в которой вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа.
• Позиционной системой счисления называется система, в которой вес каждой цифры измеряется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.

Непозиционная система счисления

• Римская система является современной непозиционной системой счисления. До сих пор римские числа очень часто используются.
• В ней для записи различных целых чисел используются символы

I, V, X, L, C, D, M и т.д., обозначающие соответственно

1, 5, 10, 50,100,500,1000 и т.д.

• Если слева от старшей цифры стоит младшая, то она отнимается. Если младшая цифра стоит справа от старшей, то она прибавляется.

• XXVIII =10+10+5+1+1+1=28
• MCMLXXXV = запишите самостоятельно

= 1985

Общий недостаток непозиционных систем

• это сложность представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр.
• В ЭВМ применяют только позиционные системы счисления.

Позиционная система счисления

Определения

Алфавит – это множество используемых цифр в данной системе.

Основание системы счисления –это размер алфавита (число цифр).

Какой системой счисления пользуемся мы?

Мы используем цифры 0,1,2,3,4,5,6,7,8,9 – это алфавит системы;

Всего цифр 10 – это основание системы, поэтому система называется десятичной.

Виды позиционных систем

• Традиционные Р- ичные
• Смешанные Р- Q- ичные
• Нетрадиционные

Позиционная система счисления

• Каждая позиционная система определяется набором цифр и основанием. Добавление нуля означает умножение на 10 поэтому говорят, что в основании используемой нами системы счисления лежит число 10, или по-другому – десять – основание системы счисления, а сама система называется десятичная.

246 = 200 + 40 + 6 =2*100+4*10+6*1=

=2*10 2 +4*10 1 +6*10 0

4957829=

4000000+900000+50000+7000+800+20+9=

4•10 6 +9•10 5 +5•10 4 +7•10 3 + 8•10 2 + 2•10 1 + 9•10 0

Позиционная система счисления

246 = 200 + 40 + 6 = 2 * 10 2 + 4 * 10 1 + 6 * 10 0

• можно записать общую формулу представления десятичного числа. Пусть дано число, в котором N цифр. Будем обозначать i -ю цифру через ai . Тогда число можно записать в следующем виде:

a n a n-1 ….a 2 a 1 .

Тогда форма записи числа будет выглядеть так:

a n a n-1 ….a 2 a 1 = a n *10 n-1 + a n-1 *10 n-2 + …. + a 2 *10 1 + a 1 *10 0

где a i это символ из набора " 0123456789 "

• В этой записи хорошо видна роль десятки. Десятка является основой образования числа. Она так и называется "основание системы счисления", а сама система счисления, поэтому так и называется "десятичной". Конечно, никакими особыми свойствами число десять не обладает. Мы вполне можем заменить десять на любое другое число.

Позиционная система счисления

• Например, число в пятеричной системе счисления можно записать так:

a n a n-1 ….a 2 a 1 = a n *5 n-1 + a n-1 *5 n-2 + …. + a 2 *5 1 + a 1 *5 0

где a i это символ из набора " 01234 "

• Заменяем 10 на любое другое число и получаем совершенно другую систему счисления и другую арифметику. Наиболее простая арифметика получается, если 10 заменить на 2. Полученная система счисления называется двоичной и число в ней определяется следующим образом:

a n a n-1 ….a 2 a 1 = a n *2 n-1 + a n-1 *2 n-2 + …. + a 2 *2 1 + a 1 *2 0

  где a i это символ из набора " 01 "

• Эта система самая простая из всех возможных, так как в ней любое число образуется только из двух цифр 0 и 1. Понятно, что проще уже некуда.
• Примеры двоичных чисел : 10 2 , 111 2 , 101 2 .

Двоичное в десятичное

• Метод перевода даёт наш способ записи чисел. Возьмём, к примеру, следующее двоичное число 1011 . Разложим его по степеням двойки. Получим следующее:

1011 2 = 1 * 2 3 + 0 * 2 2 + 1 * 2 1 + 1 * 2 0

Выполним все записанные действия и получим:

1 * 2 3 + 0 * 2 2 + 1 * 2 1 + 1 * 2 0 = 8 + 0+ 2 + 1 = 11 .

• Получаем, что 1011(двоичное) = 11 (десятичное).
• Ответ: 1011 2 = 11 10

неудобство двоичной системы.

• число, которое, в десятичной системе записано одним знаком в двоичной системе, для своей записи требует четыре знака.
• Но это плата за простоту. Но выигрыш двоичная система даёт огромный в арифметических действиях. И далее мы это увидим.

Представьте в виде десятичного числа следующие двоичные числа.

а) 10010 2

б) 11101 2

в ) 1010 2

г) 1110 2

д) 100011 2

е) 1100111 2

ж) 1001110 2

= 18 10

= 29 10

= 10 10

= 14 10

= 35 10

= 103 10

= 78 10

Позиционная система счисления

• Количество цифр, используемых в системе счисления для записи чисел, называется ее основанием.
• Если количество таких цифр равно P , то система счисления называется P -ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления.
• Запись произвольного числа x в P -ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена

x = a n P n +a n -1 P n -1 + ... +a 1 P 1 +a 0 P 0 +a -1 P -1 + ... +a -m P -m

• Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и десятичной системе

Позиционная система счисления

Поскольку за основание системы счисления можно принять любое натуральное число, то существует бесчисленное множество позиционных систем счисления.

Историческая справка

• Люди предпочитают десятичную систему счисления вероятно потому, что с древних времен они считали по пальцам, а пальцев у людей по 10 на руках и ногах.
• Десятичная система счисления пришла к нам из Индии.

Историческая справка

• Не всегда и везде используют десятичную систему счисления. В Китае, например, долгое время пользовались пятеричной системой счисления. В Вавилоне существовала двенадцатеричная система счисления.
• Для общения с ЭВМ используют, кроме десятичной, двоичную, восьмеричную и шестнадцатеричную системы счисления.

Позиционные системы счисления

Название системы

Основание

Двоичная

Троичная

Алфавит

2

3

Четверичная

0,1

0,1,2,

4

Пятеричная

5

0,1,2,3

Восьмеричная

Десятичная

0,1,2,3,4

8

10

0,1,2,3,4,5,6,7

Двенадцатеричная

0,1,2,3,4,5,6,7,8,9

12

Шестнадцатеричная

16

0,1,2,3,4,5,6,7,8,9,А,В

Тридцатишестиричная

0,1,2,3,4,5,6,7,8,9,А,В,С, D,E,F

36

0,1,2,3,4,5,6,7,8,9 , А,В,С, D,E,F,G, H,I,J,K,L,M,N,O,P,R,S,T,U,V,X,Y,Z

Слово великим…

Король Швеции Карл XII был поклонником восьмеричной и шестнадцатеричной систем счисления, считая что они ближе к «самой природе».

Слово великим…

Д. И. Менделеев очень интересовался уравновешенной троичной системой, может быть поэтому он открыл знаменитую формулу спирта.

Вильгельм Готфрид Лейбниц (1646-1716)

• Начиная со студенческих лет и до конца жизни великий Лейбниц занимался исследованием свойств двоичной системы счисления, ставшей в дальнейшем основной при создании компьютеров. Он придавал ей некий мистический смысл и считал, что на ее базе можно создать универсальный язык для объяснения явлений мира и использования во всех науках, в том числе в философии.
• Сохранилось изображение медали, поясняющее соотношение между двоичной и десятичной системами исчисления:
• На ней была изображена табличка из двух столбцов, в одном числа от 0 до 17 в десятичной системе, а в другом – те же числа в двоичной системе счисления. Вверху была надпись: «2,3,4,5 и т.д. Для получения их всех из нуля достаточно единицы». Внизу же гласила надпись: «Картина создания. Изобрёл ГГЛ. МDС XCYII».

Вильгельм Готфрид Лейбниц

М едал ь , нарисованн ая В. Лейбницем в 1697 г., поясняющ ая соотношение между двоичной и десятичной системами исчисления

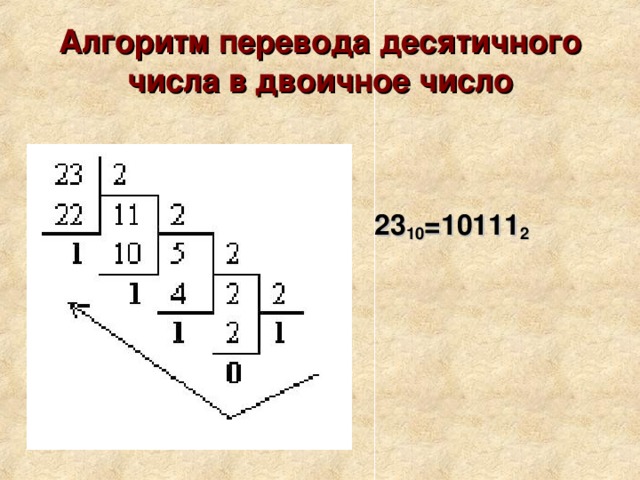
Алгоритм перевода десятичного числа в двоичное число

23 10 =10111 2

Представьте в виде двоичного числа следующие десятичные числа.

а) 15 10

б) 27 10

в) 134 10

г) 158 10

д) 1190 10

е) 2019 10

=1111 2

= 11011 2

= 10000110 2

= 10011110 2

= 10010100110 2

= 11111100011 2

НЕОБЫКНОВЕННАЯ ДЕВОЧКА

Ей было тысяча сто лет,

Она в сто первый класс ходила,

В портфеле по сто книг носила.

Все это правда, а не бред.

Когда, пыля десятком ног,

Она шагала по дороге.

За ней всегда бежал щенок

С одним хвостом, зато стоногий.

Она ловила каждый звук

Своими десятью ушами,

И десять загорелых рук

Портфель и поводок держали.

И десять темно-синих глаз

Рассматривали мир привычно,

Но станет все совсем обычным,

Когда поймете мой рассказ.

/Н. Стариков/

• Догадайтесь, о какой девочке идет речь?
• И сколько же лет было девочке? В какой она класс ходила? Сколько у нее рук и ног было? Откуда у щенка 100 ног?

Это интересно

• Скажите, какое число и в какой системе счисления фигурирует в известной восточной сказке? (1001 ночь)
• Сколько это будет, если перевести в десятичную систему счисления?

Время в двоичной системе.

• В Японии поступили в продажу необычные электронные часы, отображающие время в двоичной системе счисления.
• Выглядят часы также довольно необычно. Они заключены в круглый металлический корпус, однако вместо циферблата со стрелками или индикатора с цифрами под стеклом находится печатная плата зеленого цвета с резисторами, конденсаторами и расположенными в два ряда десятью светодиодами. Именно они и показывают время.

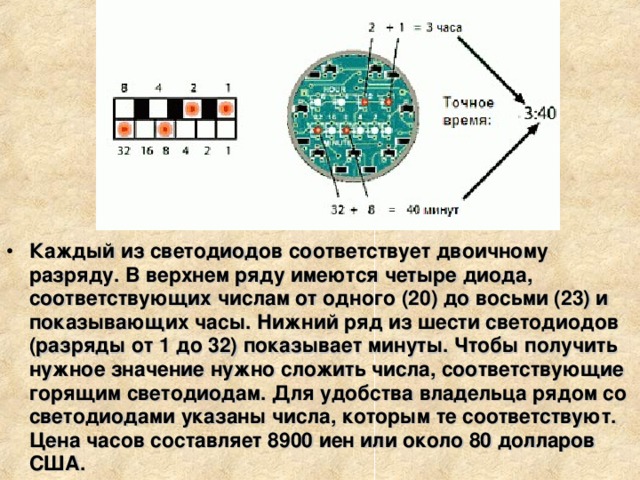
• Каждый из светодиодов соответствует двоичному разряду. В верхнем ряду имеются четыре диода, соответствующих числам от одного (20) до восьми (23) и показывающих часы. Нижний ряд из шести светодиодов (разряды от 1 до 32) показывает минуты. Чтобы получить нужное значение нужно сложить числа, соответствующие горящим светодиодам. Для удобства владельца рядом со светодиодами указаны числа, которым те соответствуют. Цена часов составляет 8900 иен или около 80 долларов США.

Задание на дом

Перевести в десятичную

систему счисления

• 10011 – ?10
• 10111 – ?10

Перевести в двоичную

систему счисления

• 4110 – ?2
• 1710 – ?2