Презентация к уроку математики «Цилиндр»

Содержание:

История.

Где можно встретить цилиндр?

Что такое цилиндр?

Виды цилиндров.

Прямой круговой цилиндр.

Свойства цилиндра.

Виды сечений.

Площадь прямого кругового цилиндра.

Объём цилиндра.

Решение задач.

Вопросы.

История.

Слово "цилиндр" произошло от греческого слова "кюлиндрос", означающего "валик", "каток". На рубеже XVIII – XIX веков мужчины многих стран носили твёрдые шляпы с небольшими полями, которые так и назывались цилиндрами из-за большого сходства с геометрической фигурой цилиндром.

Где можно встретить цилиндр?

Цилиндры в архитектуре.

Пизанская башня.

Бродвейская башня.

Московский кремль.

Цилиндрические здания.

Башня Геркулеса в городе Лос-Барриос.

Штаб-квартира BMW в Мюнхене.

Круглое, квадратное и треугольное здания в Тель-Авиве.

Что такое цилиндр?

Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.

Цилиндр

Содержание

• История
• Где можно встретить цилиндр?
• Что такое цилиндр?
• Виды цилиндров
• Прямой круговой цилиндр
• Свойства цилиндра
• Виды сечений
• Площадь прямого кругового цилиндра
• Объём цилиндра
• Решение задач
• Вопросы

История

Слово "цилиндр" произошло от греческого слова "кюлиндрос", означающего "валик", "каток". На рубеже XVIII – XIX веков мужчины многих стран носили твёрдые шляпы с небольшими полями, которые так и назывались цилиндрами из-за большого сходства с геометрической фигурой цилиндром.

Где можно встретить цилиндр?

Цилиндры в архитектуре

Московский кремль

Бродвейская башня

Пизанская башня

Цилиндрические здания

Башня Геркулеса в городе Лос-Барриос.

Штаб-квартира BMW   в Мюнхене

Круглое, квадратное и треугольное здания в Тель-Авиве

Цилиндры в быту

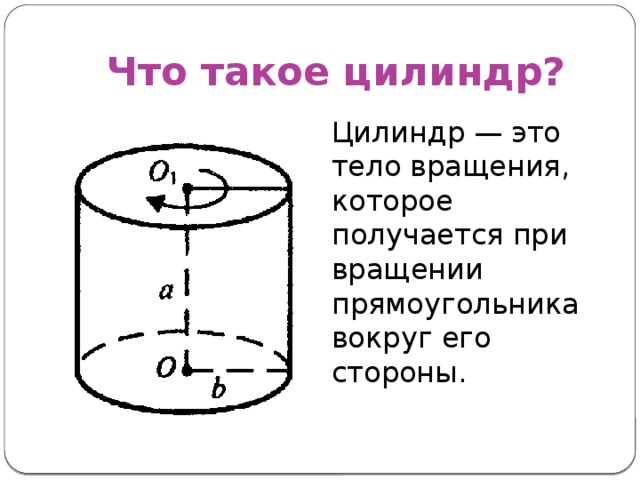
Что такое цилиндр?

Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.

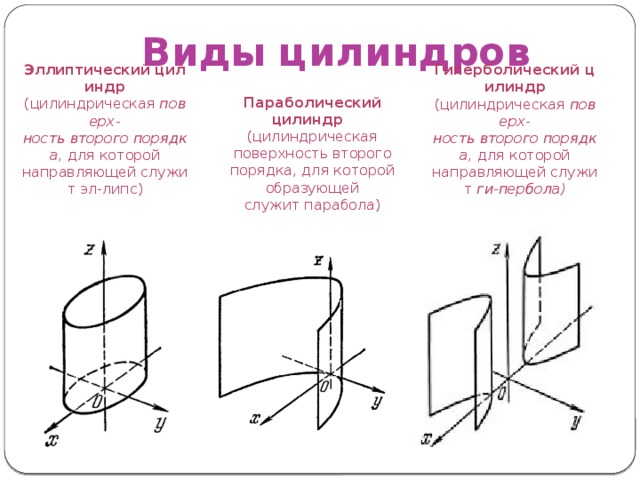
Виды цилиндров

Эллиптический   цилиндр (цилиндрическая  поверх-ность второго порядка,  для которой направляющей служит эл-липс)

Параболический цилиндр  

Гиперболический цилиндр (цилиндрическая  поверх-ность второго порядка,  для которой направляющей служит  ги-пербола)

(цилиндрическая поверхность второго порядка, для которой образующей служит парабола)

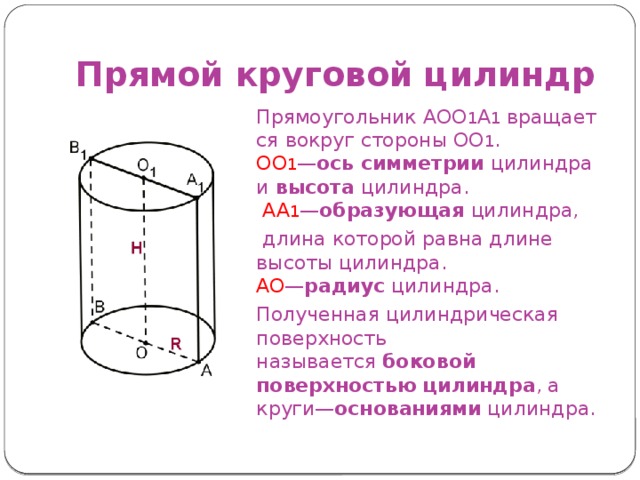
Прямой круговой цилиндр

Прямоугольник AOO 1 A 1  вращается вокруг стороны OO 1 . OO 1 — ось симметрии  цилиндра и  высота  цилиндра. AA 1 — образующая  цилиндра,

  длина которой равна длине высоты цилиндра. AO — радиус  цилиндра.

Полученная цилиндрическая поверхность называется  боковой поверхностью цилиндра , а круги— основаниями  цилиндра.

Свойства цилиндра

1) Основания равны и параллельны ;

2) Все образующие цилиндра параллельны и равны друг другу;

Перпендикуляр, опущенный из любой точки одного основания цилиндра на плоскость другого его основания, называется высотой цилиндра.

3) Все высоты цилиндра параллельны и равны друг другу.

Виды сечений

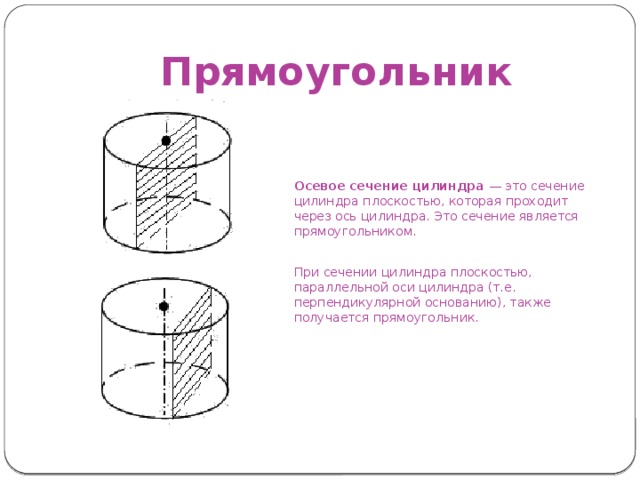
Прямоугольник

Осевое сечение цилиндра  — это сечение цилиндра плоскостью, которая проходит через ось цилиндра. Это сечение является прямоугольником.

При сечении цилиндра плоскостью, параллельной оси цилиндра (т.е. перпендикулярной основанию), также получается прямоугольник.

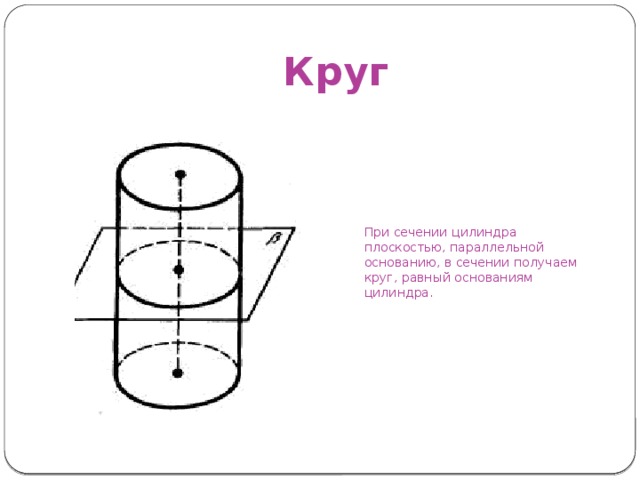
Круг

При сечении цилиндра плоскостью, параллельной основанию, в сечении получаем круг, равный основаниям цилиндра.

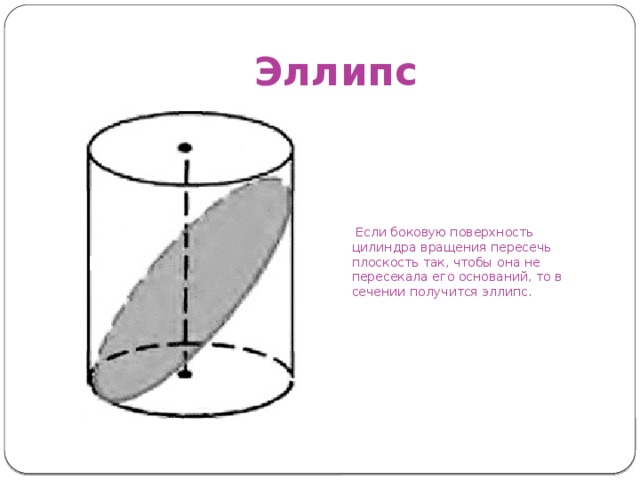
Эллипс

  Если боковую поверхность цилиндра вращения пересечь плоскость так, чтобы она не пересекала его оснований, то в сечении получится эллипс.

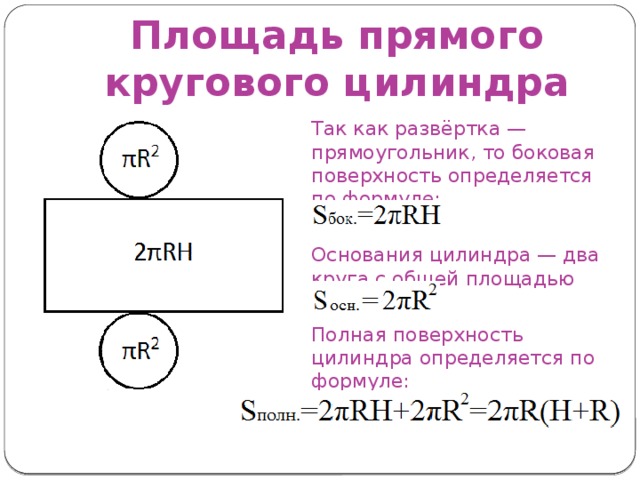
Площадь прямого кругового цилиндра

Так как развёртка — прямоугольник, то боковая поверхность определяется по формуле:

Основания цилиндра — два круга с общей площадью 

Полная поверхность цилиндра определяется по формуле:

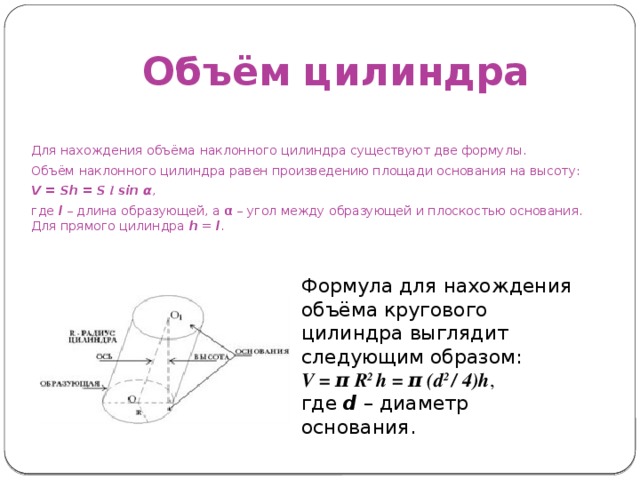
Объём цилиндра

Для нахождения объёма наклонного цилиндра существуют две формулы.

Объём наклонного цилиндра равен произведению площади основания на высоту:

V = Sh = S l sin α ,

где l  – длина образующей, а α  – угол между образующей и плоскостью основания. Для прямого цилиндра h = l .

Формула для нахождения объёма кругового цилиндра выглядит следующим образом:

V = π R 2  h = π (d 2  / 4)h ,

где d  – диаметр основания.

Решение задач

Задача №1

Площадь осевого сечения цилиндра равна 12 см ², а высота цилиндра – 2см. Найдите радиус основания.

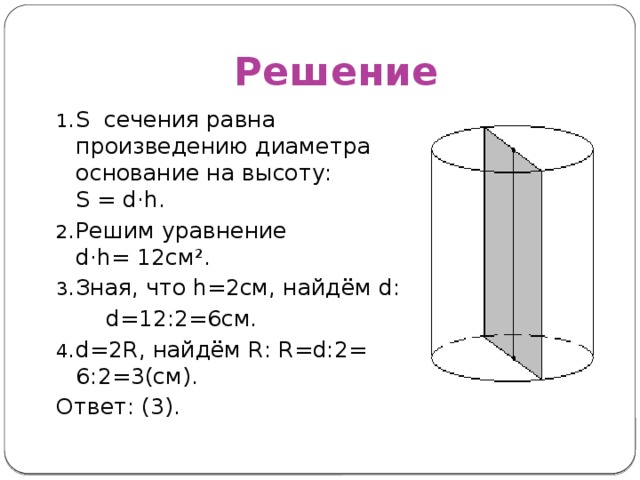
Решение

• S сечения равна произведению диаметра основание на высоту: S = d ·h.
• Решим уравнение d·h= 12см².
• Зная, что h=2cм, найдём d :

d=12:2=6см.

• d=2R, найдём R: R=d:2= 6:2=3(см).

Ответ : (3).

Задача №2

Диагональ осевого сечения цилиндра равна √89 см, а радиус основания – 4см. Найдите высоту цилиндра.

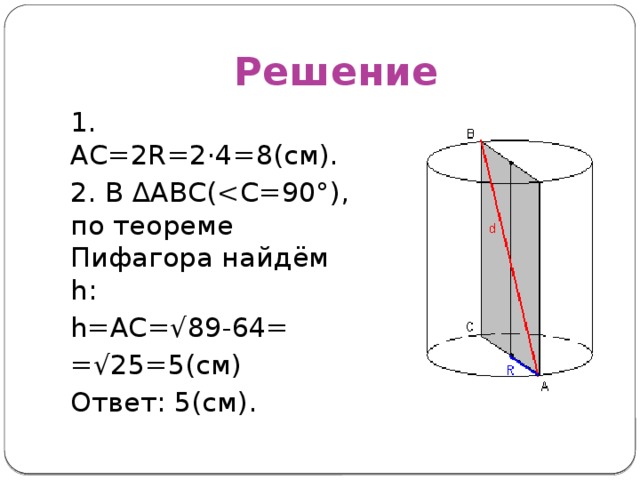
Решение

1. АС=2R=2 ·4=8(см).

2. В ∆АВС(

h=AC=√89-64=

=√25=5(cм)

Ответ: 5(см).

Задача №3

Вычислить площадь поверхности цилиндра, если его высота 5 см, а радиус оснований 2 см.

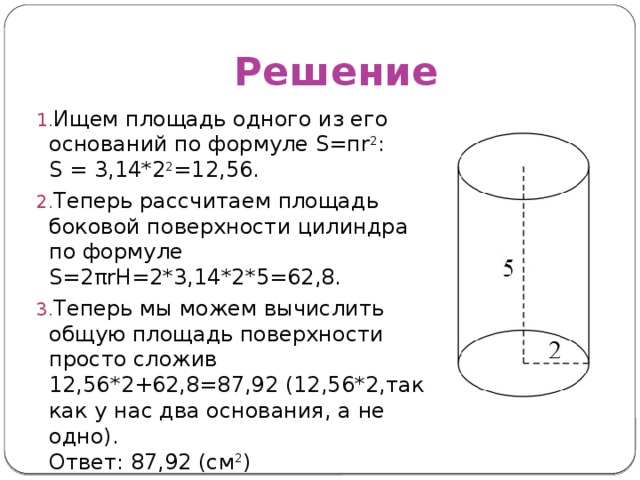
Решение

• Ищем площадь одного из его оснований по формуле S=пr 2 : S = 3,14*2 2 =12,56.
• Теперь рассчитаем площадь боковой поверхности цилиндра по формуле S=2πrH=2*3,14*2*5=62,8.
• Теперь мы можем вычислить общую площадь поверхности просто сложив 12,56*2+62,8=87,92 ( 12,56*2, так как у нас два основания, а не одно).   Ответ: 87,92 (см 2 )

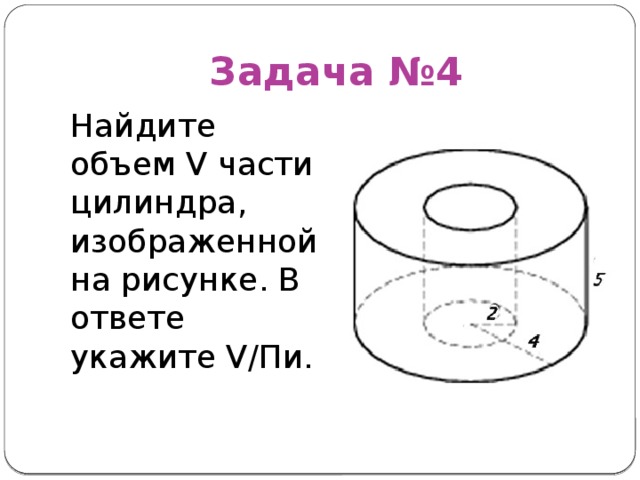
Задача №4

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

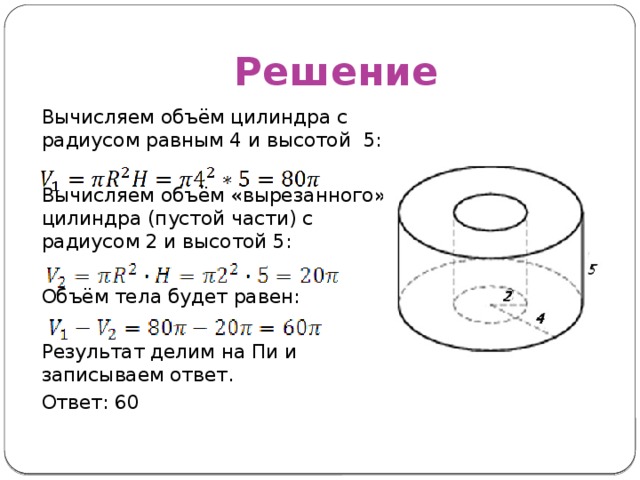
Решение

Вычисляем объём цилиндра с радиусом равным 4 и высотой  5:

Вычисляем объём «вырезанного» цилиндра (пустой части) с радиусом 2 и высотой 5:

Объём тела будет равен:

Результат делим на Пи и записываем ответ.

Ответ: 60

Вопросы

• Что из себя представляют основания цилиндра?
• Что вы можете сказать о размерах этих кругов?
• Что из себя представляет боковая поверхность?

Урок окончен!