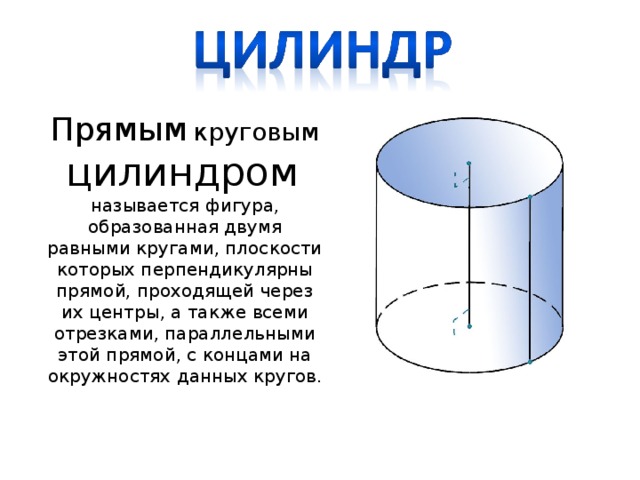
Прямым круговым цилиндром называется фигура, образованная двумя равными кругами, плоскости которых перпендикулярны прямой, проходящей через их центры, а также всеми отрезками, параллельными этой прямой, с концами на окружностях данных кругов
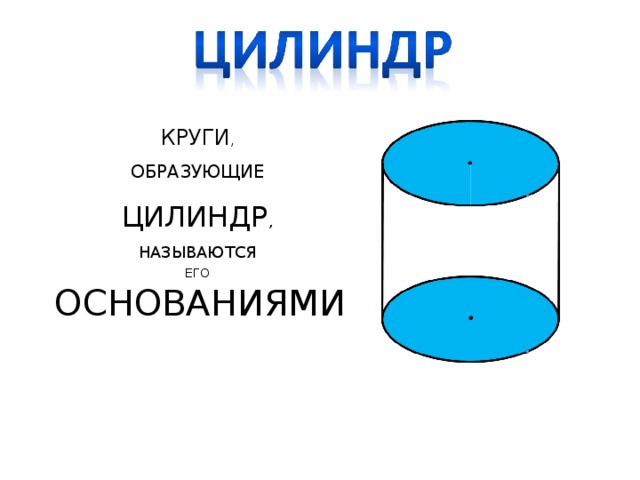
КРУГИ, ОБРАЗУЮЩИЕ ЦИЛИНДР, НАЗЫВАЮТСЯ ЕГО ОСНОВАНИЯМИ
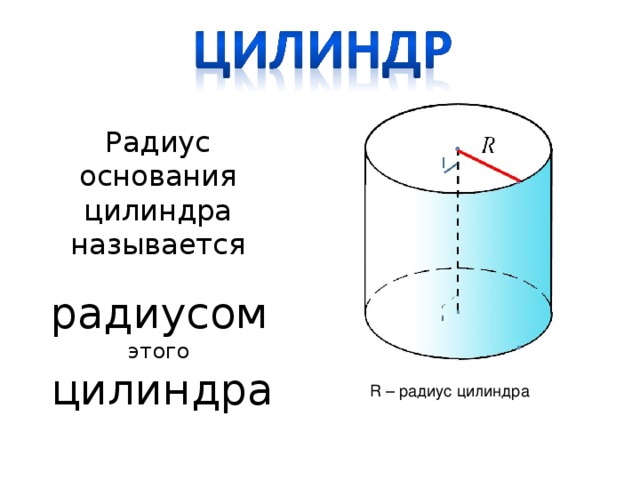
Радиус основания цилиндра называется радиусом этого цилиндра
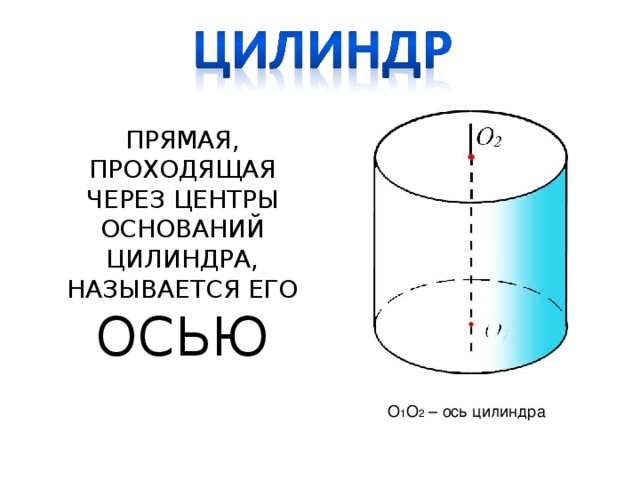
ПРЯМАЯ, ПРОХОДЯЩАЯ ЧЕРЕЗ ЦЕНТРЫ ОСНОВАНИЙ ЦИЛИНДРА, НАЗЫВАЕТСЯ ЕГО ОСЬЮ
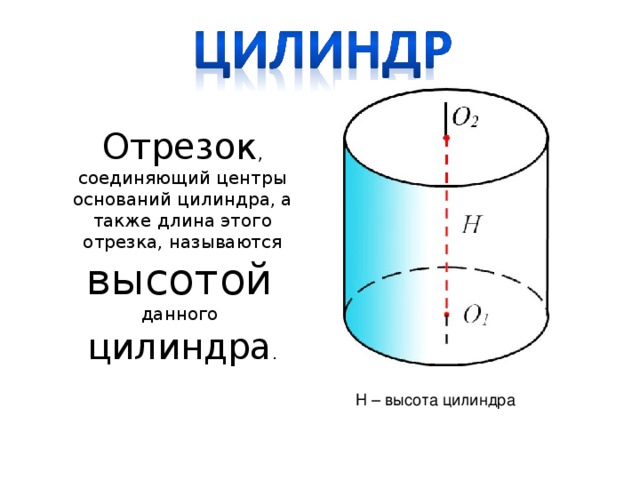
Отрезок, соединяющий центры оснований цилиндра, а также длина этого отрезка, называются высотой данного цилиндра.
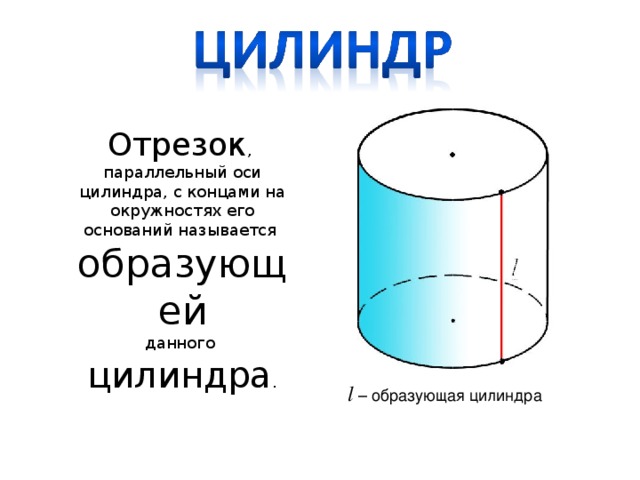
Отрезок, параллельный оси цилиндра, с концами на окружностях его оснований называется образующей данного цилиндра.
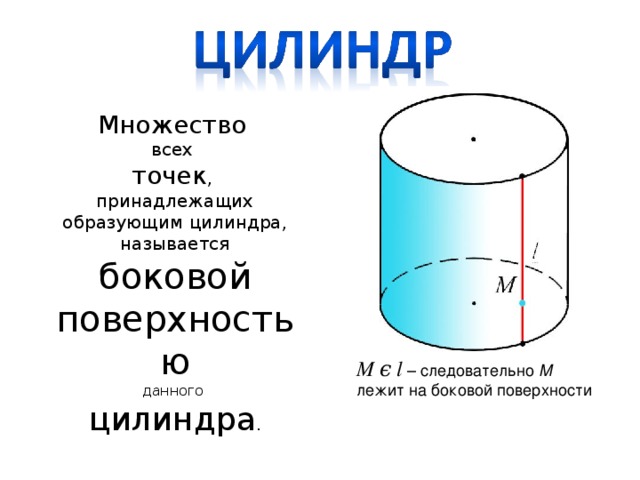
Множество всех точек, принадлежащих образующим цилиндра, называется боковой поверхностью данного цилиндра.
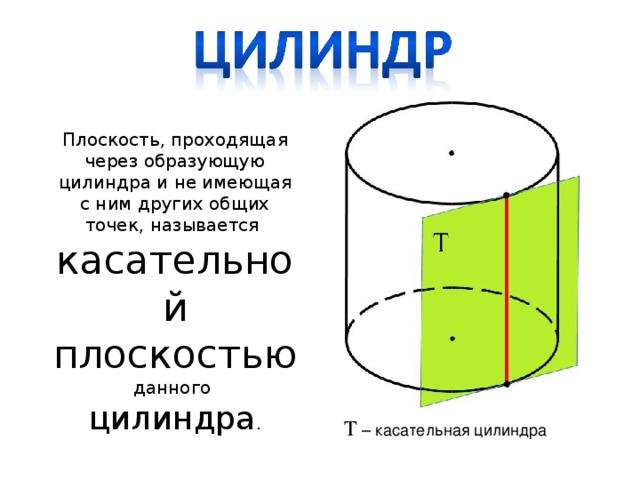
Плоскость, проходящая через образующую цилиндра и не имеющая с ним других общих точек, называется касательной плоскостью данного цилиндра.
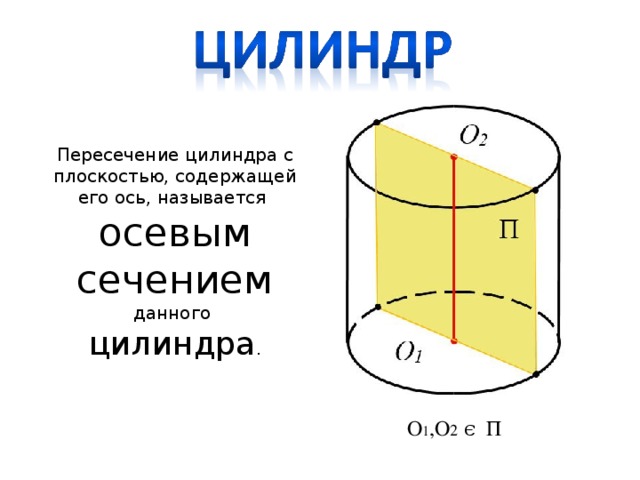
Пересечение цилиндра с плоскостью, содержащей его ось, называется осевым сечением данного цилиндра.
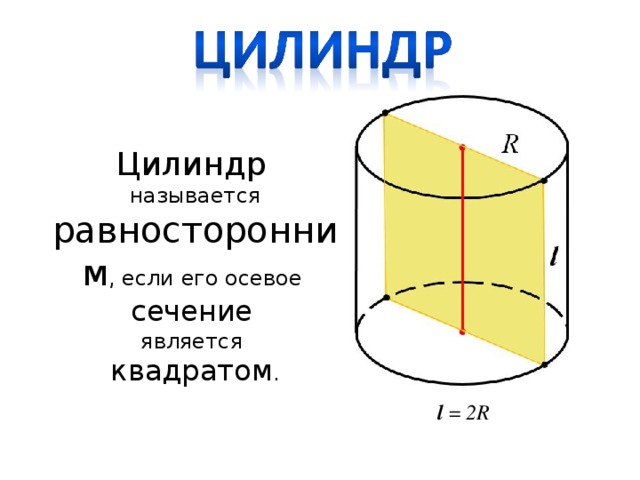
Цилиндр называется равносторонним, если его осевое сечение является квадратом.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Презентация к уроку математики "Цилиндр" (0.72 MB)
Презентация к уроку математики "Цилиндр" (0.72 MB)
 0
0 1402
1402 66
66 Нравится
0
Нравится
0


