Презентация к уроку информатики по теме Системы счисления

Данная презентация может быть использована на уроках информатики при изучении темы "Системы счисления".
Презентация включает в себя 44 слайда.

Тема урока

Системы счисления

Немного истории

На ранних ступенях развития

общества люди почти не умели

считать. Они различали совокупности

двух и трех предметов; всякая

совокупность, содержавшая бóльшее число предметов, объединялась в понятии «много». Предметы при счете сопоставлялись обычно с пальцами рук и ног.

По мере развития цивилизации потребность человека в счете стала необходимой. Первоначально натуральные числа изображались с помощью некоторого количества черточек или палочек, затем для их изображения стали использовать буквы или специальные знаки.

Узелковое письмо

Индейцы и народы Древней Азии при счете завязывали узелки на шнурках разной длины и цвета. У некоторых богатеев скапливалось по несколько метров этой веревочной "счетной книги", поди вспомни через год, что означают четыре узелочка на красном шнурочке! Поэтому того, кто завязывал узелки, называли вспоминателем.

Число — это абстрактная мера количества. Цифра — это знак для записи числа.

Существует множество способов записи чисел с помощью цифр. Эти способы можно разделить на:

• Позиционные ( мультипликативные) системы счисления;
• Смешанные системы счисления;
• Непозиционные ( аддитивные ) системы счисления.

Система счисления - способ отображения чисел и правила действий над ними .

Денежные знаки - это пример смешанной системы счисления

Около 1100 года н. э. английский король Генрих I изобрел одну из самых необычных денежных систем в истории, названную системой «мерных реек». Эта денежная система продержалась 726 лет .

Деревянная полированная рейка с зарубками, обозначающими номинал, расщеплялась по всей длине так, чтобы сохранить зарубки.

Н епозиционная система счисления

• Непозиционная система счисления - система счисления, в которой для обозначения чисел вводятся специальные знаки, количественное значение которых всегда одинаково и не зависит от их места в записи числа.

Древнеегипетская десятичная система счисления

1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки.

10. Такими путами египтяне связывали коров

100. Это мерная веревка, которой измеряли земельные участки после разлива Нила.

1 000. Вы когда-нибудь видели цветущий лотос? Если нет, то вам никогда не понять, почему Египтяне присвоили такое значение изображению этого цветка.

10 000. "В больших числах будь внимателен!" - говорит поднятый вверх указательный палец.

1 000 000. Увидев такое число, обычный человек очень удивится и возденет руки к небу. Это и изображает этот иероглиф

10 000 000. Египтяне поклонялись Амону Ра, богу Солнца, и, наверное, поэтому самое большое свое число они изобразили в виде восходящего солнца

- 1205,

- 1 023 029

Римская пятеричная система счисления

- непозиционная система счисления, в которой для записи чисел используются буквы латинского алфавита( возникла более 2500 лет у этрусков назад в Древнем Риме):

- I - означает "один"; - V - означает "пять"; - X - означает "десять"; - L - означает "пятьдесят"; - C - означает "сто"; - D - означает "пятьсот"; - M - означает "тысяча";

XXVIII =28; ХХХIХ = 39; CCCXCVII = 397; MDCCCXVIII = 1818.

Выполнение арифметических

действий над многозначными

числами в этой записи очень трудно.

Тем не менее, римская нумерация

преобладала в Италии до 13 в ., а

в других странах Западной Европы – до 16 в .

Преобразование римских чисел

Древнегреческая аттическая пятеричная система счисления

Название происходит от области Греции – Аттики со столицей Афины. В этой системе числа 1, 2, 3, 4 изображались соответствующим количеством вертикальных полосок:

Число 5 записывалось знаком

(древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте").

Числа 6, 7, 8, 9 обозначались

сочетаниями этих знаков:

Число 10 обозначалось

заглавной "Дельта" от слова "дека" -"десять".

Древнегреческая ионийская десятичная алфавитная система счисления

Возникла в Милеете (греческая малоазиатская колония Ионии). В ней числа 1 - 9 обозначаются первыми буквами древнегреческого алфавита:

Для отличия цифр и букв писали черточки над цифрами.

Славянская глаголическая десятичная система счисления

• Эта система была создана для обозначения чисел в священных книгах западных славян.

Использовалась она с VIII по XIII в.

2

10

3

90

4

20

5

100

30

6

200

40

50

7

300

8

400

800

60

9

900

500

70

600

80

700

- 863

Славянская кириллическая десятичная алфавитная

Тысяча

Тьма

1000

Легион

10 000

100 000

Ворон

Леодр

1 000 000

10 000 000

Колода

100 000 000

Славянская нумерация просуществовала до конца XVII столетия.

Древнеиндийские системы счисления

• Система счисления кхарошти имела хождение в Индии между VI веком до нашей эры и III веком нашей эры.

Наряду с этой системой существовала в Индии еще одна система счисления брахми .

Недостатки непозиционной системы счисления

• 1.     Существует постоянная  потребность введения новых знаков для записи больших чисел.
• 2. Невозможно представлять дробные и отрицательные числа.
• 3.    Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения .

П озиционные системы счисления

• Позиционная система счисления (возникла в Шумере (на территории современного Ирака) в период 4 и 3 тысячелетий до н. э.) - система счисления, использующая для записи чисел ограниченное число знаков, интерпретация которых зависит от места в записи числа.
• Место каждой цифры в числе называется позицией .
• Количество цифр используемых в системе счисления называется основанием.
• Место для цифры, использованное в записи числа, называется разрядом , а количество цифр в числе- разрядностью.

Позиционные системы счисления

• двоичная система счисления;
• система счисления с основанием е=2,718281828;
• троичная система счисления;
• пятеричная система счисления (у

ряда африканских племен и в

Древнем Китае );

• семеричной системе счисления;
• восьмеричная система счисления;
• двенадцатеричная система счисления;
• шестнадцатеричная система счисления;
• двадцатеричная система (у древних ацтеков и майя, и среди населявших Западную Европу древних кельтов) ;
• шестидесятеричная (вавилонская) система счисления (00, 01, 02, ..., 59)

Вавилонская десятичная / шестидесятеричная

• В древнем Вавилоне примерно во II тысячелетие до нашей эры была такая система счисления - числа менее 60 обозначались с помощью двух знаков: д ля единицы, и для десятка.

• Лишь в V веке до нашей эры был введен особый знак - наклонный клин для обозначения пропущенных разрядов, игравший роль нуля.

- 20;

- 3;

- 59

302

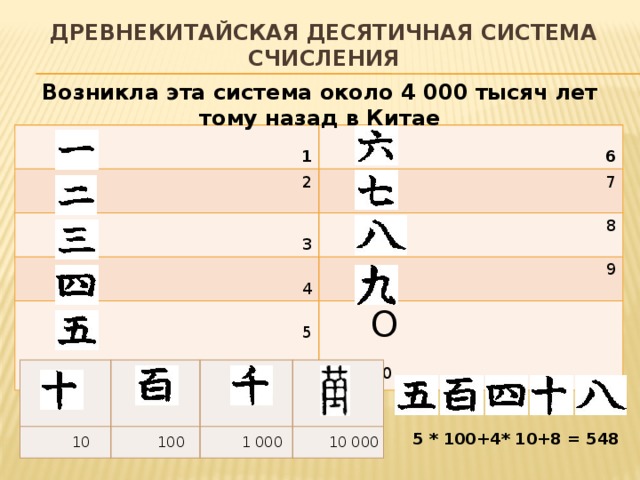
Древнекитайская десятичная система счисления

Возникла эта система около 4 000 тысяч лет тому назад в Китае

1

2

6

7

3

8

4

9

5

O 0

10

100

1 000

10 000

5 * 100+4* 10+8 = 548

.

Двадцатеричная система счисления индейцев Майя или долгий счет

• Эта система применялась для календаря и астрономических наблюдений. Характерной особенностью ее было наличие нуля (изображение ракушки). Число 20 изображалось из двух цифр, ноль и один наверху и называлось уиналу
• число 21, это будет

.

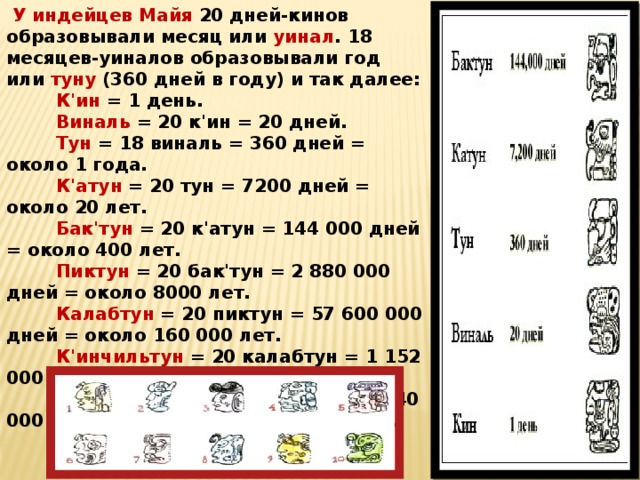
У индейцев Майя 20 дней-кинов образовывали месяц или уинал . 18 месяцев-уиналов образовывали год или туну (360 дней в году) и так далее:

      К'ин = 1 день.          Виналь = 20 к'ин = 20 дней.          Тун = 18 виналь = 360 дней = около 1 года.          К'атун = 20 тун = 7200 дней = около 20 лет.          Бак'тун = 20 к'атун = 144 000 дней = около 400 лет.          Пиктун = 20 бак'тун = 2 880 000 дней = около 8000 лет.          Калабтун = 20 пиктун = 57 600 000 дней = около 160 000 лет.          К'инчильтун = 20 калабтун = 1 152 000 000 дней = около 3200000 лет.          Алавтун = 20 к'инчильтун = 23 040 000 000 дней = около 64 000 000 лет.

Календарь народа Майя

Цифры календаря народа Майя

• Более удобной и общепринятой и наиболее распространенной является индо-арабская десятичная система счисления , которая была изобретена в Индии, заимствована там арабами и затем через некоторое время пришла в Европу (0, 1, 2, 3, 4, 5, 6, 7, 8 и 9).

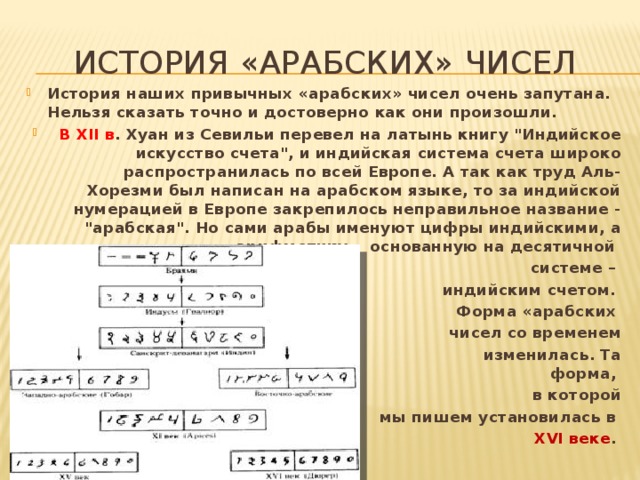
История «арабских» чисел

• История наших привычных «арабских» чисел очень запутана. Нельзя сказать точно и достоверно как они произошли.
• В XII в . Хуан из Севильи перевел на латынь книгу "Индийское искусство счета", и индийская система счета широко распространилась по всей Европе. А так как труд Аль- Хорезми был написан на арабском языке, то за индийской нумерацией в Европе закрепилось неправильное название - "арабская". Но сами арабы именуют цифры индийскими, а арифметику, основанную на десятичной

системе –

индийским счетом.

Форма «арабских

чисел со временем

изменилась. Та форма,

в которой

мы пишем установилась в

XVI веке .

Такими были наши числа

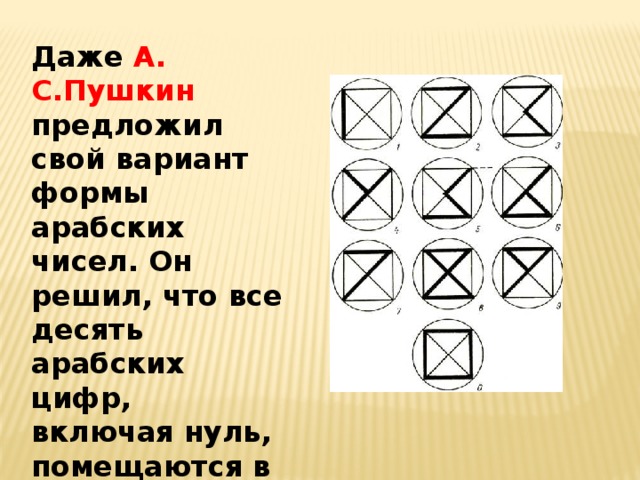
Даже А. С.Пушкин предложил свой вариант формы арабских чисел. Он решил, что все десять арабских цифр, включая нуль, помещаются в магическом квадрате.

История нуля

Впервые нуль появился в древневавилонской системе счисления, он использовался для обозначения пропущенных разрядов в числах . Изобретателем формы нуля можно считать великого греческого астронома Птолемея . Но Птолемей использует нуль в том же смысле, что и вавилоняне.

Леонардо Фибоначчи, в своем сочинении "Liber abaci" (1202) называет знак 0 по-арабски zephirum. Слово zephirum – это арабское слово as-sifr, которое произошло от индийского слова sunya, т. е. пустое, служившего названием нуля. От слова zephirum произошло французское слово zero (нуль) и итальянское слово zero. С другой стороны, от арабского слова as-sifr произошло русское слово цифра. Вплоть до середины XVII века это слово употреблялось специально для обозначения нуля. Латинское слово nullus (никакой) вошло в обиход для обозначения нуля в XVI веке .

Выполните Задания

• Пирог нужно печь в духовке 45 минут, сколько это будет в секундах?
• Нужно испечь десять пирогов, сколько потребуется времени?

Двоичная система счисления

• В двоичной системе счисления всего две цифры, называемые двоичными (binary digits). В двоичной системе основание равно 2, а алфавит состоит из двух цифр (0 и 1).

Из истории

• Двоичной системой счисления пользовался в начале 17 в. Т.Харриот . Позднее Г.Лейбниц обратил на двоичную систему внимание миссионеров, отправлявшихся для проповеди христианства в Китай в надежде убедить китайского императора в том, что Бог (единица) сотворил все из ничего (нуля). Однако вплоть до 20 в . двоичную систему рассматривали как своего рода математический курьез, и время от времени раздавались предложения перейти от десятичной системы к восьмеричной или двенадцатеричной, но отнюдь не к двоичной системе.

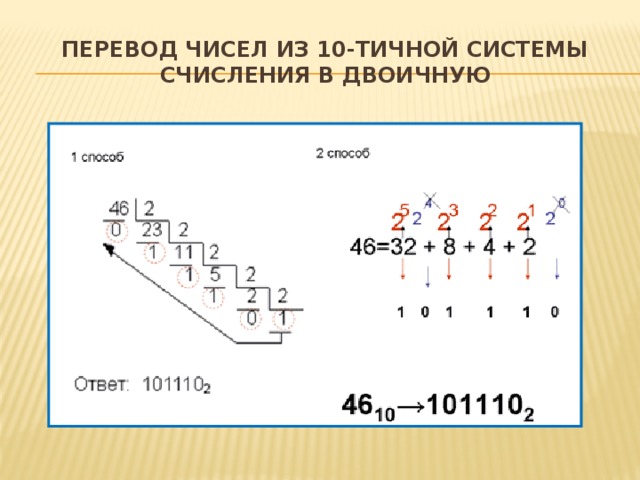
Перевод чисел из 10-тичной системы счисления в двоичную

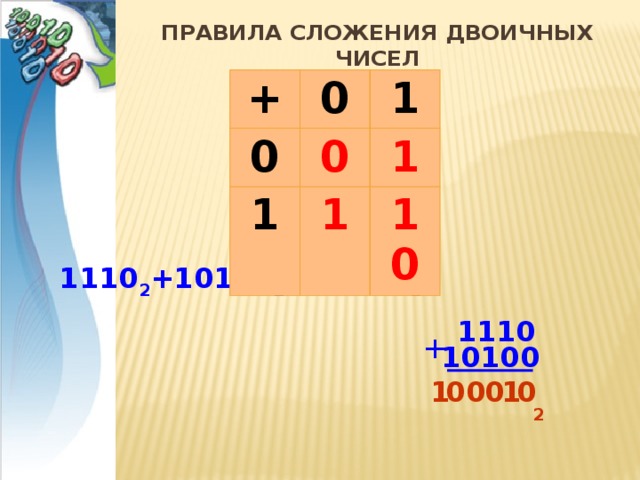
Правила Сложения двоичных чисел

+

0

0

1

0

1

1

1

10

100010 2

1110 2 +10100 2 =

1110

+

10100

0

1

0

1

0

0

2

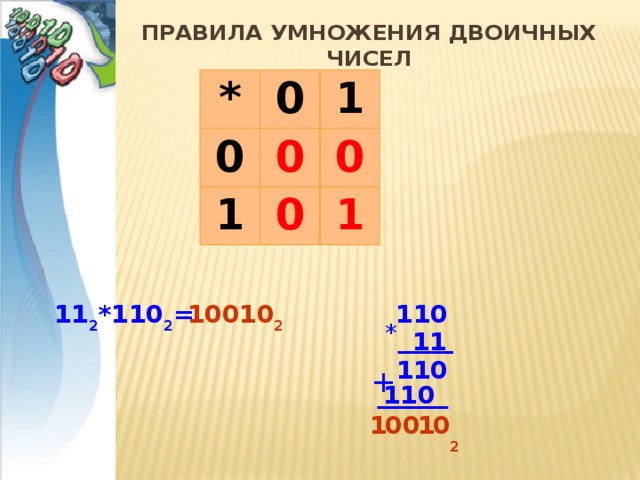
Правила умножения двоичных чисел

*

0

0

1

1

0

0

0

1

110

10010 2

11 2 *110 2 =

*

11

110

+

110

1

0

1

0

0

2

Задания

1) Переведите целые числа из десятичной системы счисления в двоичную.

а) 45 б) 124

1111100

101101

2) Переведите целые числа из двоичной системы в десятичную.

а) 11010 б) 10010010

146

26

Восьмеричная система счисления

• В восьмеричной (octal) системе счисления используются восемь различных цифр 0, 1, 2, 3, 4, 5, 6, 7. Основание системы - 8.
• В различных языках программирования запись восьмеричных чисел начинается с 0, например, запись 011 означает число 9.

Перевод чисел из 10-тичной системы счисления в восьмеричную

Шестнадцатеричная система счисления

В шестнадцатеричной (hexadecimal) системе счисления применяется десять различных цифр и шесть первых букв латинского алфавита

(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).

A - 10; B – 11; C – 12; D – 13; E – 14; F - 15

Шестнадцатеричная система счисления широко используется при задании различных оттенков цвета при кодировании графической информации (модель RGB ).

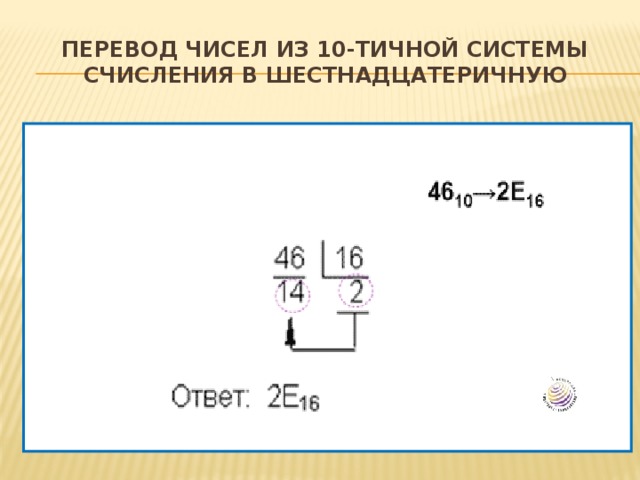
Перевод чисел из 10-тичной системы счисления в шестнадцатеричную

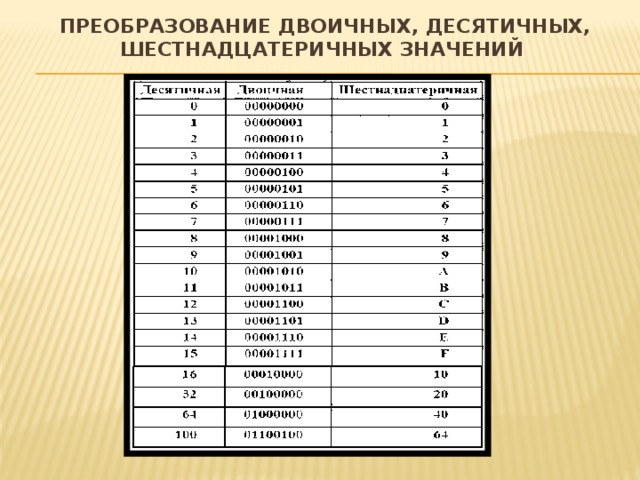
Преобразование двоичных, десятичных, шестнадцатеричных значений

Развёрнутая форма записи числа

• В позиционной СС любое целое число может быть представлено в виде:

А р = ± (a 0 р 0 + a 1 р 1 + a 2 р 2 +…+ a n-2 р n-2 + a n-1 · р n-1 ),

где А – само число,

р – основание СС,

а i – цифры данного числа,

n – число разрядов целой части числа

Например:

1 пример:

А 8 = 7564 8 = 4·8 0 + 6·8 1 + 5·8 2 + 7·8 3 = 4+ 48+ 320+ 3584 = 3956 10

Разряд  3 2 1 0

Таким способом можно перевести число из любой СС в десятичную СС.

2 пример:

10011 2 = 1·2 0 + 1·2 1 + 0·2 2 +0·2 3 +1·2 4 = 1 + 2 + 0 + 0 + 16 = 19 10

Разряд  4 3 2 1 0

• Переведите из десятичной в двоичную, восьмеричную и шестнадцатеричную системы счисления свою дату рождения.
• Разгадайте слово:

• Переведите числа, записанные в различных системах счисления, в десятичную систему счисления; затем полученные после вычисления числа замените буквами русского алфавита, которые имеют соответствующие порядковые номера; запишите полученное слово
• Переведите числа, записанные в различных системах счисления, в десятичную систему счисления;
• затем полученные после вычисления числа замените буквами русского алфавита, которые имеют соответствующие порядковые номера;
• запишите полученное слово

Достоинства позиционных систем счисления

• Простота выполнения арифметических операций

• Ограниченное количество символов для записи числа

• Удобна для механического представления чисел

Интересные факты

• В настоящее время, в полном виде или в виде следов и остатков прежнего употребления, 5-ричная система счисления употребляется у 26 племен Африки , 8 — Полинезии , 13 — Азии и 30 — Америк и; 20-ричная у 4 племен Африки, 3 — Полинези и, 18 — Азии , 8 — Америки и 6 — Европы.

Н а циферблате этих часов цифры, конечно, есть, но они написаны в двоичной системе счисления. З ато эти часы помогут научиться считать до двенадцати в двоичной системе с закрытыми глазами.