Основы логики
ФОРМЫ МЫШЛЕНИЯ
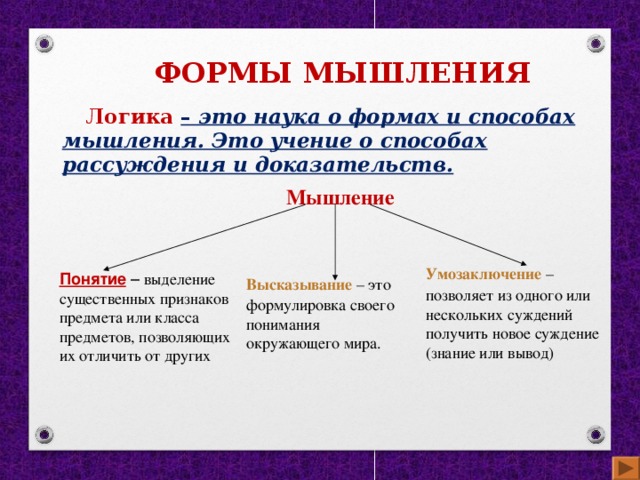
Логика – это наука о формах и способах мышления. Это учение о способах рассуждения и доказательств.
Мышление
Умозаключение – позволяет из одного или нескольких суждений получить новое суждение (знание или вывод)
Понятие – выделение существенных признаков предмета или класса предметов, позволяющих их отличить от других
Высказывание – это формулировка своего понимания окружающего мира.
ФОРМЫ МЫШЛЕНИЯ
Какие из предложений являются высказываниями?
Определить их истинность.
- Какой длины эта лента?
- Прослушайте сообщение.
- Делайте утреннюю зарядку!
- Назовите устройство ввода информации.
- Кто отсутствует?
- Париж — столица Англии.
- Число 11 является простым.
- 4 + 5 = 10.
- Без труда не вытащишь и рыбку из пруда.
- Сложите числа 2 и 5.
- Некоторые медведи живут на севере.
- Все медведи - бурые.
- Чему равно расстояние от Москвы до Ленинграда?
ФОРМЫ МЫШЛЕНИЯ
Все углы равнобедренного треугольника равны
Получить высказывание:
«Этот треугольник равносторонний», путем умозаключений.
.
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ОПЕРАЦИИ
Алгебра — это наука об общих операциях, аналогичных сложению и умножению, которые выполняются не только над числами, но и над другими математическими объектами, в том числе и над высказываниями. Такая алгебра называется алгеброй логики.
Алгебра логики отвлекается от смысловой содержательности высказываний и принимает во внимание только истинность или ложность высказывания.
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ОПЕРАЦИИ
- Логическая переменная — это простое высказывание, содержащее только одну мысль. Ее символическое обозначение — латинская буква (например A , B , X , Y и т.д.). Значением логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 и 0).
- Составное высказывание — логическая функция , которая содержит не сколько простых мыслей, соединенных между собой с помощью логических операций. Ее символическое обозначение — F ( A , B ,...).
- Логические логическое действие.
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ОПЕРАЦИИ
Базовые логические операции
конъюнкция
отрицание
дизъюнкция
дополнительные логические операции
эквивалентность
импликация
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ОПЕРАЦИИ
Логическое выражение - это составное высказывание (логическая функция) выраженная в виде формулы, в которую входят логические переменные и знаки логических операций.
Значение логического выражения можно вычислить. Им может быть только ЛОЖЬ или ИСТИНА.
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ОПЕРАЦИИ
Порядок выполнения логических операций:
- действия в скобках;
- инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ОПЕРАЦИИ
«Летом Петя поедет в деревню,
и если будет хорошая погода,
то он пойдет на рыбалку».
Простые высказывания
«Петя поедет в деревню»
«Он пойдет на рыбалку»
«Будет хорошая погода»
А = Петя поедет в деревню;
В = Будет хорошая погода;
С = Он пойдет на рыбалку.
F = А&(В С)
Основные логические операции
Конъюнкция
(от лат. conjunction — связываю)
Название
Логическое
умножение
Обозначение
Дизъюнкция (от лат. disjunction -различию)
Логическое сложение
Инверсия (от лат. inversion – перевора-чиваю)
А&В или А ^ В
Отрицание
Имплика-ция (от лат. imputation — тесно связывать)
A B
¬ А или
Логическое следование
Эквивалент-ность (от лат . equivalents -равноценно)
Логическое равенство
А→В
А - условие
В - следствие
А ≡ В или А↔ В
Симанова Т.С.
Основные логические операции
Союз в естественном языке
А и В
Примеры
А «Число 10 - четное»;
В -«Число 10 –отрицатель-ное»
«Число 10 четное и отри-
цательное» - ЛОЖЬ
А или В
Не А
«Число 10 — четное или отрицательное» — ИСТИНА
«Неверно, что число 10- четное» ЛОЖЬ «Неверно, что число 10 отрица-тельное» - ИСТИНА
Если А. то В; когда А, тогда В; коль скоро А то и В; и т.п.
А тогда и только тогда, когда В
«Если число 10 — четное, то оно является отрицательным» = ЛОЖЬ
«Число 10 -четное тогда и только тогда; когда отрицатель-но» = ЛОЖЬ
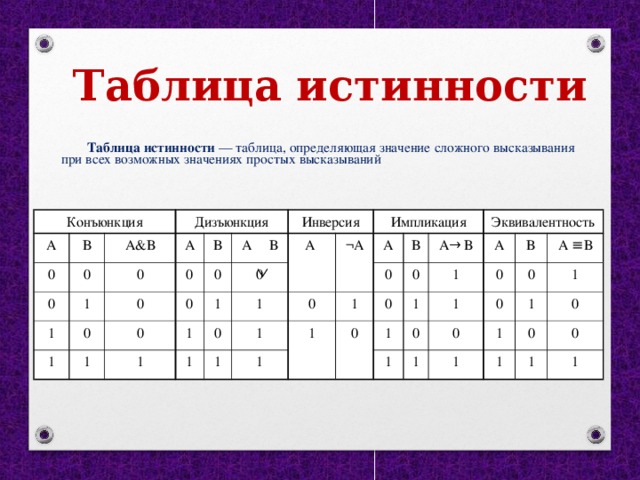
Таблица истинности
Таблица истинности — таблица, определяющая значение сложного высказывания при всех возможных значениях простых высказываний
Конъюнкция
A
0
B
Дизъюнкция
А&В
0
0
A
0
1
1
B
0
1
0
0
0
0
1
0
А В
Инверсия
1
1
A
0
1
Импликация
0
1
¬ А
1
1
A
1
0
0
B
1
1
1
0
А→ В
0
0
Эквивалентность
1
A
1
1
B
1
0
1
0
0
1
А ≡ В
0
0
1
1
1
1
0
1
0
1
0
1
Выводы Основные логические операции
Конъюнкция
Дизъюнкция
Вывод: результат будет истинным тогда и только тогда, когда оба исходных высказывания истинны
Инверсия
Вывод: результат будет ложным тогда и только тогда, когда оба исходных высказывания ЛОЖНЫ, и ИСТИННЫ в остальных случаях
Импликация
Вывод: результат будет ложным, если исходное выражение истинно, и наоборот
Эквивалентность
Вывод: результат будет ложным тогда и только тогда, когда из истинного основания (А) следует ложное следствие (В)
Вывод: результат будет истинным тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны
Получите свидетельство
Вход
Презентация к уроку информатике по теме: "Основы логики" (12.22 MB)
0
1315
63
Нравится
0
