Презентация к уроку геометрии "Первый признак равенства треугольников"

Два треугольника называются равными, если их можно совместить наложением.

Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.

Два треугольника равны, если каждый из них можно наложить на другой так, что их вершины и стороны попарно совместятся.

Если треугольники равны, то элементы одного  треугольника соответственно равны элементам другого треугольника.

AB = A₁B₁, BC = B₁C₁, CA = C₁A₁

угол A = угол A₁, угол B = угол B₁, угол C = угол C_1.

В

А

С

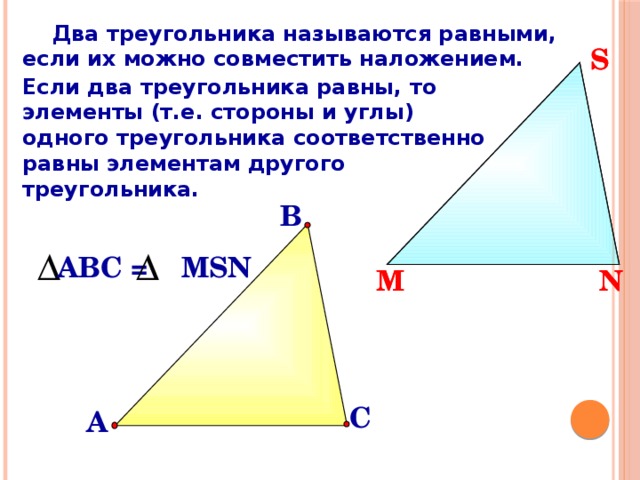
Два треугольника называются равными, если их можно совместить наложением.

S

S

Если два треугольника равны, то элементы (т.е. стороны и углы)

одного треугольника соответственно равны элементам другого треугольника.

В

АВС = MSN

N

М

N

М

С

А

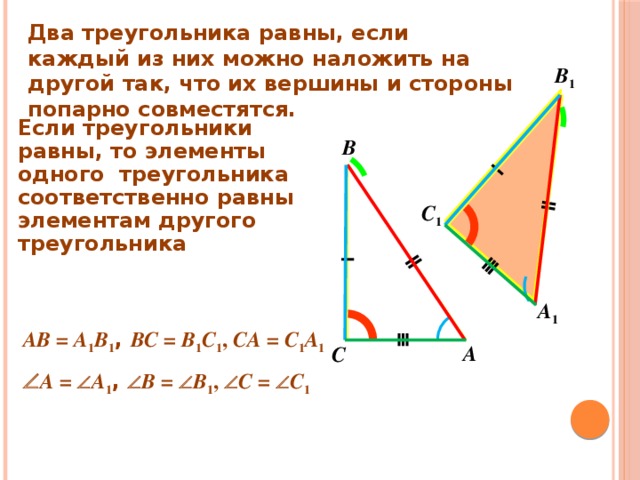
Два треугольника равны, если каждый из них можно наложить на другой так, что их вершины и стороны попарно совместятся.

B 1

Если треугольники равны, то элементы одного треугольника соответственно равны элементам другого треугольника

B

C 1

A 1

AB = A 1 B 1 , BC = B 1 C 1 , CA = C 1 A 1

A

C

 A =  A 1 ,  B =  B 1 ,  C =  C 1

3

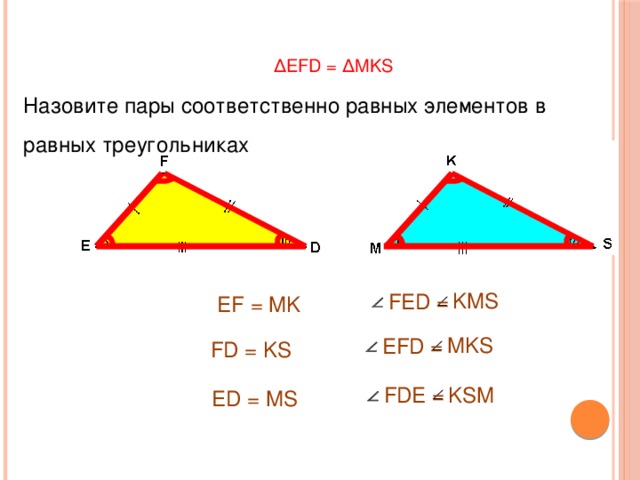
∆ EFD = ∆MKS

Назовите пары соответственно равных элементов в равных треугольниках

KMS

FED =

EF = MK

MKS

EFD =

FD = KS

KSM

FDE =

ED = MS

12/16/16

Первый признак равенства треугольников

Теорема - это высказывание правильность которого установлена при помощи рассуждения, доказательства.

Аксиома - это первоначальные факты геометрии, которые принимаются без доказательства.

Первый признак равенства треугольников

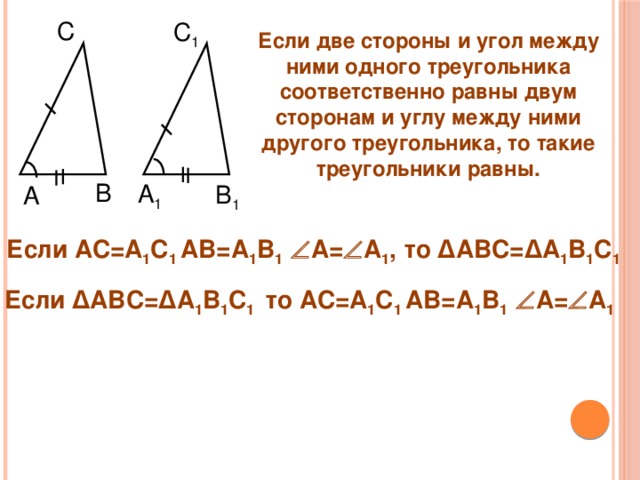
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

С

C 1

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

B

A 1

B 1

A

Если АС=А 1 С 1 АВ=А 1 В 1  А=  А 1 ,

то ∆АВС=∆А 1 В 1 С 1

Если ∆АВС=∆А 1 В 1 С 1

то АС=А 1 С 1 АВ=А 1 В 1  А=  А 1

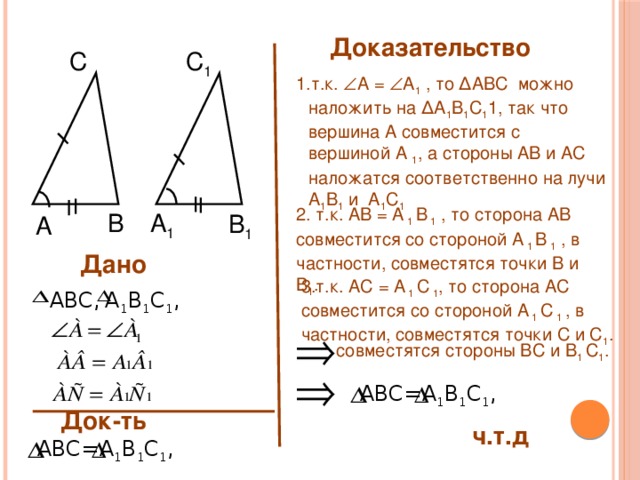
Доказательство

С

C 1

• т.к.  А =  A 1 , то ∆ABC можно наложить на ∆A 1 B 1 C 1 1, так что вершина А совместится с вершиной A 1 , а стороны АВ и АС наложатся соответственно на лучи A 1 B 1 и A 1 C 1

2. т.к. АВ = A 1 B 1 , то сторона АВ совместится со стороной A 1 B 1 , в частности, совместятся точки В и B 1 .

B

A 1

B 1

A

Дано

3.т.к. АС = A 1 C 1 , то сторона АС совместится со стороной A 1 C 1 , в частности, совместятся точки С и C 1 .

А 1 В 1 С 1 ,

ABC,

совместятся стороны ВС и В 1 C 1 .

ABC=

А 1 В 1 С 1 ,

Док-ть

ч.т.д

А 1 В 1 С 1 ,

ABC=

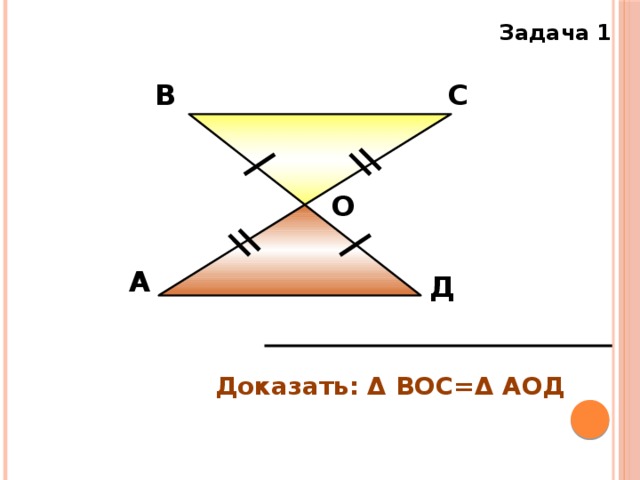
Задача 1

В

С

О

А

Д

Доказать: Δ ВОС=Δ АОД

В

С

А

Д

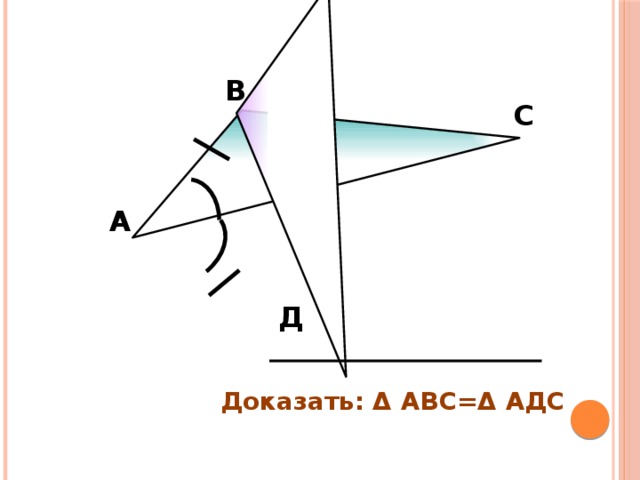
Доказать: Δ АВС=Δ АДС

Домашнее задание

п15 № 89(а), № 95(а)