Актуальность и новизна данной темы очевидна и неоспорима. В нашем мире компьютерных технологий, где уже часто используются термины «умный телевизор», «умный телефон», «умный дом» и т. д. , образование не может оставаться в стороне, чтобы не оказаться на обочине научно - технического прогресса и современной жизни развивающегося в сторону мультимедийных инноваций общества. Государству просто необходимы высококвалифицированные специалисты в различных отраслях деятельности, которые без боязни будут использовать компьютерные технологии и сопутствующие им ресурсы. И помочь им в этом должны и мы – преподаватели СПО и НПО. Сегодня с повсеместной информатизацией образования часто употребляется термин «мультимедийный урок», «конструирование мультимедийного урока». Осваивая данную технологию, предметник в поисках материала обращается к опыту коллег, пытаясь применять чьи - то очень удачные наработки. И это не всегда приводит к положительному результату. Почему?
Потому, что готовых рецептов конструирования мультимедийного урока до сих пор нет. Причин здесь много: и недостаток опыта, и отсутствие достаточной методической и, если хотите, методологической составляющей. Учитель настойчиво ищет методические рекомендации, практические советы, как подготовить эффективный мультимедийный урок? А информатизация предоставляет всё более новые и интересные возможности, программы, готовые продукты. И мы понимаем, да – всё это - то, да не совсем. И педагог опять возвращается к необходимости самостоятельно конструировать мультимедиа уроки.
Однако, прежде всего, при проектировании таких уроков необходимо задать себе вопрос, данная технология необходима именно на этом уроке?
Мультимедийный урок не должен быть самоцелью!
При проектировании будущего мультимедийного урока разработчик должен задуматься над тем, какие цели он преследует, какую роль этот урок играет в системе уроков по изучаемой теме или всего учебного курса. Для чего предназначен мультимедийный урок, на каком этапе урока можно применить данную технологию:
для изучения нового материала, предъявления новой информации;
для закрепления пройденного, отработки учебных умений и навыков;
для повторения, практического применения полученных знаний, умений навыков;
для обобщения, систематизации знаний?
Будет ли от такого урока та отдача, которую мы ждём от безграничных возможностей данной технологии. Мультимедийный урок может достичь максимального обучающего эффекта, если он предстанет осмысленным цельным продуктом, а не случайным набором слайдов.
Следует отметить, что для использования данной технологии необходимо усвоить ряд простых правил. А совершенствоваться можно путём самообразования в дальнейшем.
Итак, правило №1. Выбор фона – залог успеха!
Правило №2. Презентация – это НЕ учебник. Не забивайте её текстом. Текст менеее 18 – нечитаемый!
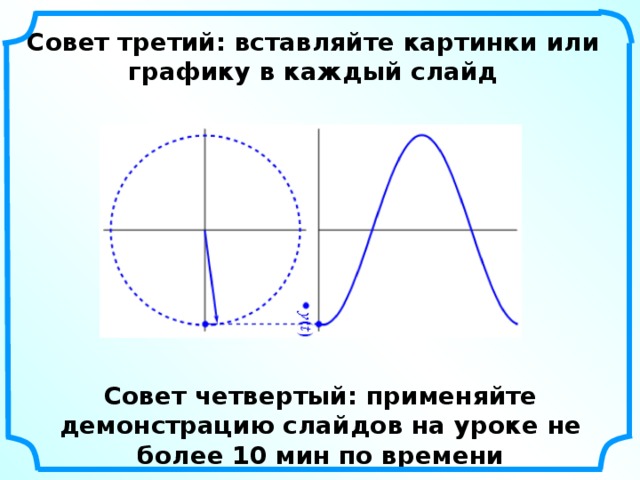
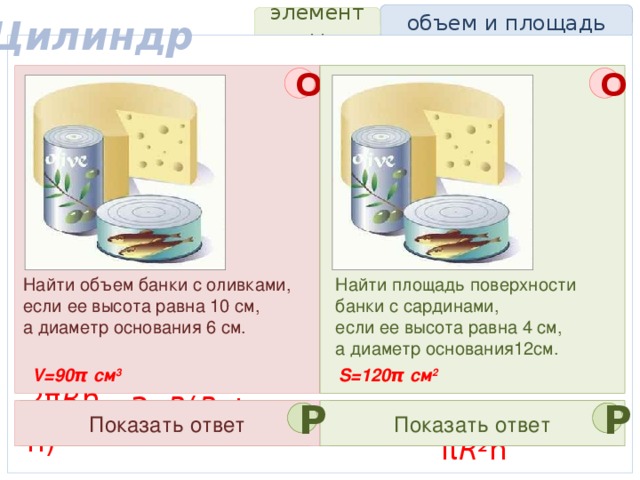
Правило №3. Картинки и графика должны нести информационную нагрузку. Если картинки вставляются для украшения - они только отвлекают!
Фотографии, рисунки могут быть полноцветными, а вот векторная графика, которую мы часто применяем (линии, фигуры) должны соответствовать основной цветовой схеме выбранного шаблона презентации.
Правило №4. Опыт работы показывает, что если все составные части урока, виды работ (вступление, объяснение нового материала, самостоятельная работа, устный счет, тестирование и др. ) реализуются посредством демонстрации слайдов, то эффект от этого минимальный.
Если приходится, например, использовать слайды при объяснении нового материала и организации устного счета, то между этими видами работ нужно заняться чем - то другим без компьютера, можно порешать задачи у доски.
Конечно, если проводится урок - лекция в старших классах, то демонстрация слайдов длится столько, сколько по времени продолжается лекция
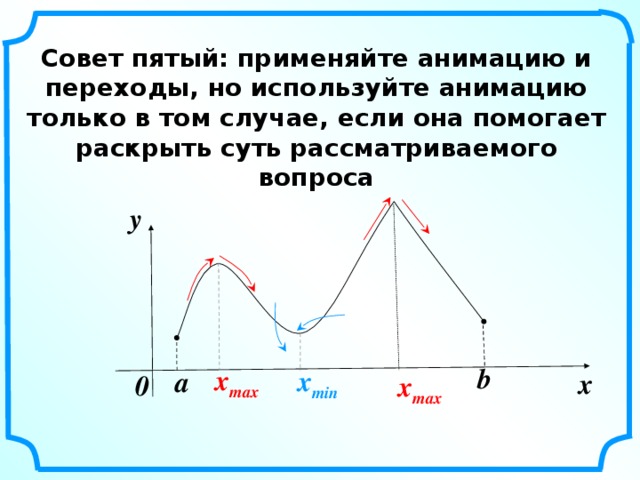
Правило №5. Огромную роль в информационных продуктах, которые мы создаем и используем на уроках математики играет анимация. С помощью ее можно показать динамику демонстрируемой системы, оживить задачи, чертежи.
Не нужно использовать анимацию, особенно анимационные картинки для привлечения внимания учащихся. Математическая мысль, логическая цепочка не должна прерываться ничем.
Я не стану останавливаться на таких общих, основополагающих моментах как эргономика презентации, требования к оформлению презентации.

Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход







![функция возрастает Предположим, что функция f не имеет на отрезке [а; b] критических точек. Тогда она возрастает (рис. 1) или убывает (рис. 2) на этом отрезке. Значит, наибольшее и наименьшее значения функции f на отрезке [а; b] — это значения в концах а и b. наибольшее значение наименьшее значение a b функция убывает http://www.terver.ru/maththeoryAlgebra.php наибольшее значение Тема: «Наибольшее и наименьшее значение функции» Этап: Изучение нового материала наименьшее значение a b 10](https://fsd.videouroki.net/html/2014/09/24/98686997/img9.jpg)
![Примеры Пусть теперь функция f имеет на отрезке [а; b] конечное число критических точек. Наибольшее и наименьшее значения функция f может принимать в критических точках функции или в точках а и b. Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее. наибольшее значение наименьшее значение c a b наибольшее значение наибольшее значение http://www.terver.ru/maththeoryAlgebra.php наименьшее значение наименьшее значение c n a b 11](https://fsd.videouroki.net/html/2014/09/24/98686997/img10.jpg)
![Найдите наименьшее значение функции y = x 3 – 27x на отрезке [0; 4] Значения функции в концах отрезка. 1) y(0) = 0 y(4) = 4 3 – 27 4 = – 44 -3 3 2) y / = 3x 2 – 27 = 3(x 2 – 9) = 3(x – 3)(x + 3) Найдем критические точки, которые принадлежат заданному отрезку. [0; 4] x = 3 [0; 4] x = –3 Значения функции в критических точках, которые принадлежат заданному отрезку. y(3) = 3 3 – 27 3 = –54 Тема: «Наибольшее и наименьшее значение функции» Этап: Закрепление (возможно с ИД) Выбрать наименьшее из полученных значений. - 4 5 В 11 х 3 х 1 0](https://fsd.videouroki.net/html/2014/09/24/98686997/img11.jpg)











 Презентация для учителей математики "Как сконструировать мультимедиаурок" (1.52 MB)
Презентация для учителей математики "Как сконструировать мультимедиаурок" (1.52 MB)
 0
0 602
602 28
28 Нравится
0
Нравится
0


