"Правило Лопиталя"

Министерство сельского хозяйства и продовольствия Самарской области

Государственное бюджетное профессиональное образовательное учреждение

«Кинельский государственный техникум»

• Применение производной к вычислению пределов

Урок математики, 2 курс

Автор : Татьяна Владимировна Глотова преподаватель математики

ГБПОУ «КГТ»

• Применение производной к вычислению пределов

• Цель:

рассмотреть метод нахождения пределов функций, раскрывающий неопределённости вида   ; .

• Задачи:

1. Закрепить правила вычисления производных;

2. Уметь применять производную к вычислению пределов;

3. Способствовать формированию умений применять приёмы переноса знаний в новую ситуацию, развитию мышления и речи, внимания и памяти;

4. Формировать познавательный интерес к математике.

Правило Лопиталя

Правило Лопиталя  — метод нахождения пределов функций, раскрывающий неопределённости вида   ; .

Способ раскрытия такого рода неопределённостей был опубликован в учебнике «Analyse des Infiniment Petits» 1696 года за авторством Гийома Лопиталя. Метод был сообщён Лопиталю в письме его первооткрывателем Иоганном Бернулли.

  Суть правила : предел отношения функций равен пределу отношения их производных.

Правило Лопиталя

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом:

предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Правило Лопиталя можно применять неоднократно, если отношение производных снова дает неопределенность  ; .

Гийом Франсуа маркиз де Лопиталь  (1661-1704) 

Французский математик, автор первого учебника по математическому анализу.

Главная заслуга Лопиталя заключается в первом систематическом изложении математического анализа

Лопиталю принадлежит также решение ряда задач, в том числе о кривой наименьшего времени ската; о кривой, по которой должен двигаться груз, прикрепленный к цепи и удерживающий в равновесии подъемный мост. Решение этих задач помогло ему встать в один ряд с Ньютоном, Лейбницем и Якобом Бернулли

«Он был примером человека, ярчайшей особенностью которого была любовь к познанию, заставившая его посвятить большую часть своей короткой жизни написанию научных трудов». Джулиан Кулидж

Сын богатых родителей, маркиз Лопиталь поступил сперва в военную службу, но по слабости зрения вскоре оставил ее и посвятил себя наукам. Состоял членом Парижской академии наук, участник ученого кружка Мальбранша. Был женат на Мари-Шарлотт де Ромий де ла Шенелэ (фр. Marie-Charlotte de Romilley de la Chesnelaye), тоже занимавшейся математикой. В 1690-х годах занял видное место в школе Лейбница, с новым методом которого его познакомил Иоганн Бернулли в 1692 во время своего пребывания в Париже в поместье Лопиталя. Главная заслуга Лопиталя заключается в первом систематическом изложении математического анализа, данное им в сочинении «Анализ бесконечно малых» (фр. Analyse des infiniment petits pour l'intelligence des lignes courbes, 1696). В этой книге собраны и приведены в стройное целое отдельные вопросы, разбросанные до того в разных повременных изданиях, а также приводится Правило Лопиталя. В предисловии Лопиталь указывает, что без всякого стеснения пользовался открытиями Лейбница и братьев Бернулли и «не имеет ничего против того, чтобы они предъявили свои авторские права на все, что им угодно». Современников, однако, сильно озадачило то, что Иоганн Бернулли предъявил претензии на все сочинение Лопиталя целиком.

Примеры

Пример № 1

Решение:

=

=

=0

= 0

Ответ:

Пример № 2

Решение:

=

=

=

= +∞

Ответ:

= +∞

Пример № 3

Решение :

Ответ:

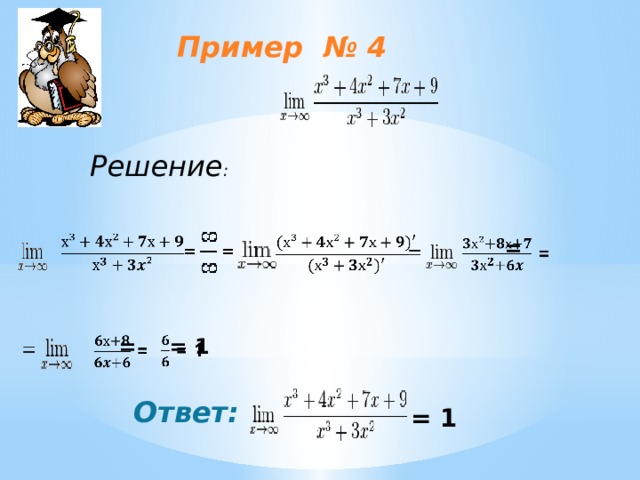
Пример № 4

Решение :

=

= 1

=

Ответ:

= 1

Выполните самостоятельно

Вариант № 1 Вариант № 2

Найдите предел Найдите предел

1

1

2

2

Ответы:

Вариант 1

Вариант 2

Вариант 1

Подставляем значение

Пределы с неопределенностью данного типа можно находить по правилу Лопиталя:

Ответ:

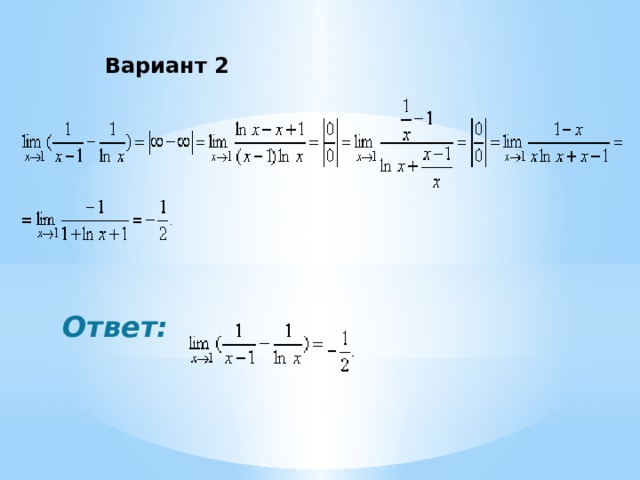
Вариант 2

Ответ:

Домашнее задание

Вычислить предел, используя правило Лопиталя

Спасибо за урок