Цели урока:
Учебные:
- повторить нахождение производных сложных функций;
- знакомство с правилом Лопиталя;
- научиться находить пределы с помощью правила Лопиталя.
Воспитательные:
- воспитывать аккуратность, краткость изложения материала;
Развивающие:
- развивать речь учащихся, требовать проговаривать каждый шаг при решении поставленной задачи;
- развивать умение анализировать, контролировать, выбирать оптимальный способ решения;
- развивать умение сравнивать полученные результаты, осуществлять проверку полученных результатов;
Тип урока: Изучение и первичное закрепление новых знаний.
Основные этапы урока:
1. Организация начала урока.
2. Проверка выполнения домашнего задания.
3. Подготовка к основному этапу занятий.
4. Усвоение новых знаний.
5. Первичная проверка понимания учащимися нового учебного материала.
6. Подведение итогов урока.
7. Информация о домашнем задании.
Ход урока:
Этап 1. Организация начала урока.
1. Приветствие.
2. Проверка готовности учеников к учебной деятельности.
3. Раскрытие общей цели урока.
Этап 2. Проверка выполнения домашнего задания.
1. Проверка правильности выполнения домашнего задания.
а) y = (9 - x2);
б) y = ln sin3x;
в) y = log3 4x;
г) y = (3x5 - x2)6;
д) y = ln2 sin2x;
е) y = log7 x3.
2. Группа выполняет задания аналогичные домашним заданиям.
а) y = (2 + 4x-2 - x-4)5;
б) y = ln sin25x;
в) y = log3 (x2 + 3x - 1).
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



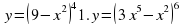
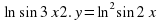
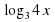 3. y=
3. y=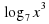
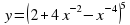
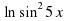
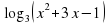
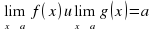 ;
;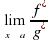 конечный или бесконечный.
конечный или бесконечный.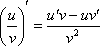 !!!
!!!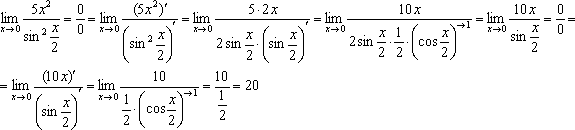









 Методическая разработка урока по математике "Применение производной к нахождению предела" (0.11 MB)
Методическая разработка урока по математике "Применение производной к нахождению предела" (0.11 MB)
 0
0 469
469 56
56 Нравится
0
Нравится
0


